【算法思想·二叉树】最近公共祖先问题
本文参考labuladong算法笔记[拓展:最近公共祖先系列解题框架 | labuladong 的算法笔记]
0、引言
如果说笔试的时候经常遇到各种动归回溯这类稍有难度的题目,那么面试会倾向于一些比较经典的问题,难度不算大,而且也比较实用。
本文就用 Git 引出一个经典的算法问题:最近公共祖先(Lowest Common Ancestor),简称 LCA。
git pull 这个命令我们经常会用,它默认是使用 merge 方式将远端别人的修改拉到本地;如果带上参数 git pull -r,就会使用 rebase 的方式将远端修改拉到本地。
这二者最直观的区别就是:merge 方式合并的分支会看到很多「分叉」,而 rebase 方式合并的分支就是一条直线。但无论哪种方式,如果存在冲突,Git 都会检测出来并让你手动解决冲突。
那么问题来了,Git 是如何检测两条分支是否存在冲突的呢?
以 rebase 命令为例,比如下图的情况,我站在 dev 分支执行 git rebase master,然后 dev 就会接到 master 分支之上:

这个过程中,Git 是这么做的:
首先,找到这两条分支的最近公共祖先 LCA,然后从 master 节点开始,重演 LCA 到 dev 几个 commit 的修改,如果这些修改和 LCA 到 master 的 commit 有冲突,就会提示你手动解决冲突,最后的结果就是把 dev 的分支完全接到 master 上面。
那么,Git 是如何找到两条不同分支的最近公共祖先的呢?这就是一个经典的算法问题了,下面我来由浅入深讲一讲。
1、寻找一个元素
先不管最近公共祖先问题,我请你实现一个简单的算法:
给你输入一棵没有重复元素的二叉树根节点 root 和一个目标值 val,请你写一个函数寻找树中值为 val 的节点。
函数签名如下:
def find(root: TreeNode, val: int) -> TreeNode:这个函数应该很容易实现对吧,比如我这样写代码:
# 定义:在以 root 为根的二叉树中寻找值为 val 的节点
def find(root: TreeNode, val: int) -> TreeNode:# base caseif not root:return None# 看看 root.val 是不是要找的if root.val == val:return root# root 不是目标节点,那就去左子树找left = find(root.left, val)if left:return left# 左子树找不着,那就去右子树找right = find(root.right, val)if right:return right# 实在找不到了return None这段代码应该不用我多解释了,我下面基于这段代码做一些简单的改写,请你分析一下我的改动会造成什么影响。
首先,我修改一下 return 的位置:
def find(root: TreeNode, val: int) -> TreeNode:if not root:return None# 前序位置if root.val == val:return root# root 不是目标节点,去左右子树寻找left = find(root.left, val)right = find(root.right, val)# 看看哪边找到了return left if left else right这段代码也可以达到目的,但是实际运行的效率会低一些,原因也很简单,如果你能够在左子树找到目标节点,还有没有必要去右子树找了?没有必要。但这段代码还是会去右子树找一圈,所以效率相对差一些。
更进一步,我把对 root.val 的判断从前序位置移动到后序位置:
def find(root: TreeNode, val: int) -> TreeNode:if root is None:return None# 先去左右子树寻找left = find(root.left, val)right = find(root.right, val)# 后序位置,看看 root 是不是目标节点if root.val == val:return root# root 不是目标节点,再去看看哪边的子树找到了return left if left is not None else right这段代码相当于你先去左右子树找,然后才检查 root,依然可以到达目的,但是效率会进一步下降。因为这种写法必然会遍历二叉树的每一个节点。
对于之前的解法,你在前序位置就检查 root,如果输入的二叉树根节点的值恰好就是目标值 val,那么函数直接结束了,其他的节点根本不用搜索。
但如果你在后序位置判断,那么就算根节点就是目标节点,你也要去左右子树遍历完所有节点才能判断出来。
最后,我再改一下题目,现在不让你找值为 val 的节点,而是寻找值为 val1 或 val2 的节点,函数签名如下:
def find(root: TreeNode, val1: int, val2: int) -> TreeNode:这和我们第一次实现的 find 函数基本上是一样的,而且你应该知道可以有多种写法,我选择这样写代码:
# 定义:在以 root 为根的二叉树中寻找值为 val1 或 val2 的节点
def find(root, val1, val2):# base caseif root is None:return None# 前序位置,看看 root 是不是目标值if root.val == val1 or root.val == val2:return root# 去左右子树寻找left = find(root.left, val1, val2)right = find(root.right, val1, val2)# 后序位置,已经知道左右子树是否存在目标值return left if left is not None else right为什么要写这样一个奇怪的 find 函数呢?因为最近公共祖先系列问题的解法都是把这个函数作为框架的。
2、秒杀五道题目
236. 二叉树的最近公共祖先
给你输入一棵不含重复值的二叉树,以及存在于树中的两个节点 p 和 q,请你计算 p 和 q 的最近公共祖先节点。
比如输入这样一棵二叉树:

如果 p 是节点 6,q 是节点 7,那么它俩的 LCA 就是节点 5:

当然,p 和 q 本身也可能是 LCA,比如这种情况 q 本身就是 LCA 节点:
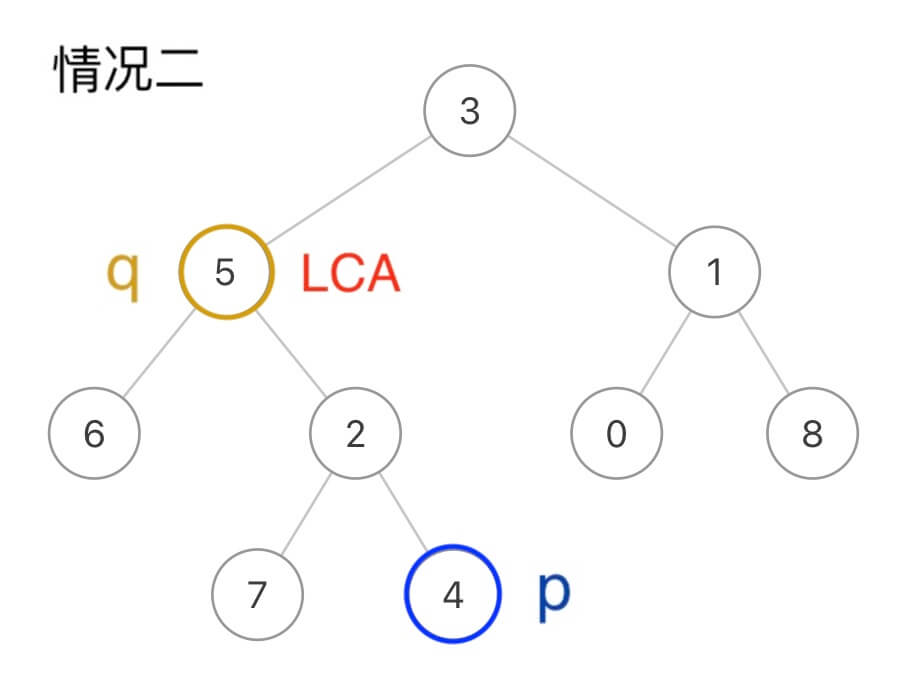
两个节点的最近公共祖先其实就是这两个节点向根节点的「延长线」的交汇点,那么对于任意一个节点,它怎么才能知道自己是不是 p 和 q 的最近公共祖先?
如果一个节点能够在它的左右子树中分别找到 p 和 q,则该节点为 LCA 节点。
这就要用到之前实现的 find 函数了,只需在后序位置添加一个判断逻辑,即可改造成寻找最近公共祖先的解法代码:
【python】
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':return self.find(root, p.val, q.val)# 在二叉树中寻找 val1 和 val2 的最近公共祖先节点def find(self, root: 'TreeNode', val1: int, val2: int) -> 'TreeNode':if not root:return None# 前序位置if root.val == val1 or root.val == val2:# 如果遇到目标值,直接返回return rootleft = self.find(root.left, val1, val2)right = self.find(root.right, val1, val2)# 后序位置,已经知道左右子树是否存在目标值if left and right:# 当前节点是 LCA 节点return rootreturn left if left else right在 find 函数的后序位置,如果发现 left 和 right 都非空,就说明当前节点是 LCA 节点,即解决了第一种情况:
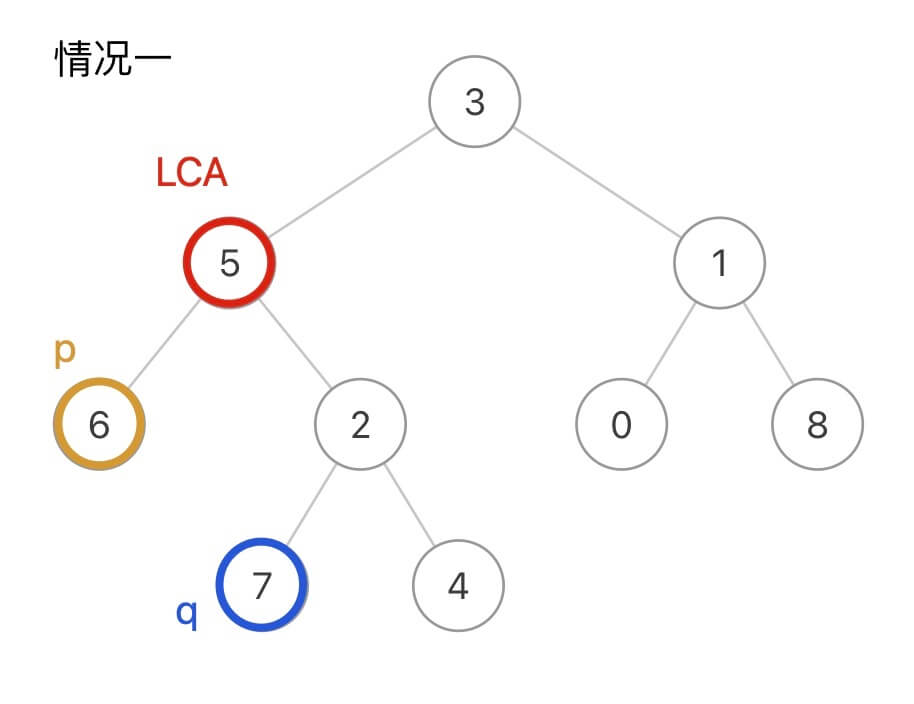
在 find 函数的前序位置,如果找到一个值为 val1 或 val2 的节点则直接返回,恰好解决了第二种情况:

因为题目说了 p 和 q 一定存在于二叉树中(这点很重要),所以即便我们遇到 q 就直接返回,根本没遍历到 p,也依然可以断定 p 在 q 底下,q 就是 LCA 节点。
这样,标准的最近公共祖先问题就解决了,接下来看看这个题目有什么变体。
1676. 二叉树的最近公共祖先 IV
依然给你输入一棵不含重复值的二叉树,但这次不是给你输入 p 和 q 两个节点了,而是给你输入一个包含若干节点的列表 nodes(这些节点都存在于二叉树中),让你算这些节点的最近公共祖先。
函数签名如下:
def lowestCommonAncestor(root: TreeNode, nodes: List[TreeNode]) -> TreeNode:比如还是这棵二叉树:
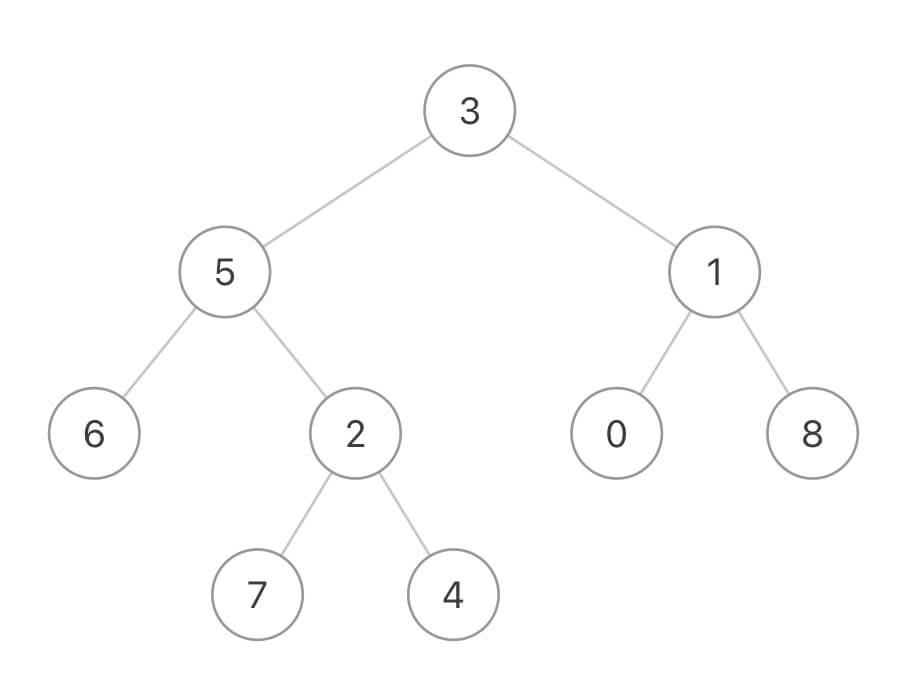
输入 nodes = [7,4,6],那么函数应该返回节点 5。
看起来怪吓人的,实则解法逻辑是一样的,把刚才的代码逻辑稍加改造即可解决这道题:
【python】
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', nodes: 'List[TreeNode]') -> 'TreeNode':# 将列表转化成哈希集合,便于判断元素是否存在values = set()for node in nodes:values.add(node.val)return self.find(root, values)def find(self, root: 'TreeNode', values: 'set') -> 'TreeNode':if not root:return None# 前序位置if root.val in values:return rootleft = self.find(root.left, values)right = self.find(root.right, values)# 后序位置,已经知道左右子树是否存在目标值if left and right:# 当前节点是 LCA 节点return rootreturn left if left else right不过需要注意的是,这两道题的题目都明确告诉我们这些节点必定存在于二叉树中,如果没有这个前提条件,就需要修改代码了。
1644. 二叉树的最近公共祖先 II
给你输入一棵不含重复值的二叉树的,以及两个节点 p 和 q,如果 p 或 q 不存在于树中,则返回空指针,否则的话返回 p 和 q 的最近公共祖先节点。
在解决标准的最近公共祖先问题时,我们在 find 函数的前序位置有这样一段代码:
// 前序位置
if (root.val == val1 || root.val == val2) {// 如果遇到目标值,直接返回return root;
}我也进行了解释,因为 p 和 q 都存在于树中,所以这段代码恰好可以解决最近公共祖先的第二种情况:

但对于这道题来说,p 和 q 不一定存在于树中,所以你不能遇到一个目标值就直接返回,而应该对二叉树进行完全搜索(遍历每一个节点),如果发现 p 或 q 不存在于树中,那么是不存在 LCA 的。
回想我在文章开头分析的几种 find 函数的写法,哪种写法能够对二叉树进行完全搜索来着?
这种:
def find(root: TreeNode, val: int) -> TreeNode:if not root:return None# 先去左右子树寻找left = find(root.left, val)right = find(root.right, val)# 后序位置,判断 root 是不是目标节点if root.val == val:return root# root 不是目标节点,再去看看哪边的子树找到了return left if left else right那么解决这道题也是类似的,我们只需要把前序位置的判断逻辑放到后序位置即可:
【python】
class Solution:def __init__(self):# 用于记录 p 和 q 是否存在于二叉树中self.foundP = Falseself.foundQ = Falsedef lowestCommonAncestor(self, root: TreeNode, p: TreeNode, q: TreeNode) -> TreeNode:res = self.find(root, p.val, q.val)if not self.foundP or not self.foundQ:return None# p 和 q 都存在二叉树中,才有公共祖先return res# 在二叉树中寻找 val1 和 val2 的最近公共祖先节点def find(self, root, val1, val2):if not root:return Noneleft = self.find(root.left, val1, val2)right = self.find(root.right, val1, val2)# 后序位置,判断当前节点是不是 LCA 节点if left and right:return root# 后序位置,判断当前节点是不是目标值if root.val == val1 or root.val == val2:# 找到了,记录一下if root.val == val1:self.foundP = Trueif root.val == val2:self.foundQ = Truereturn rootreturn left if left else right这样改造,对二叉树进行完全搜索,同时记录 p 和 q 是否同时存在树中,从而满足题目的要求。
接下来,我们再变一变,如果让你在二叉搜索树中寻找 p 和 q 的最近公共祖先,应该如何做呢?
235. 二叉搜索树的最近公共祖先
给你输入一棵不含重复值的二叉搜索树,以及存在于树中的两个节点 p 和 q,请你计算 p 和 q 的最近公共祖先节点。
把之前的解法代码复制过来肯定也可以解决这道题,但没有用到 BST「左小右大」的性质,显然效率不是最高的。
在标准的最近公共祖先问题中,我们要在后序位置通过左右子树的搜索结果来判断当前节点是不是 LCA:
对于 BST 来说,根本不需要老老实实去遍历子树,由于 BST 左小右大的性质,将当前节点的值与 val1 和 val2 作对比即可判断当前节点是不是 LCA:
假设 val1 < val2,那么 val1 <= root.val <= val2 则说明当前节点就是 LCA;若 root.val 比 val1 还小,则需要去值更大的右子树寻找 LCA;若 root.val 比 val2 还大,则需要去值更小的左子树寻找 LCA。
依据这个思路就可以写出解法代码:
【python】
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':# 保证 val1 较小,val2 较大val1 = min(p.val, q.val)val2 = max(p.val, q.val)return self.find(root, val1, val2)# 在 BST 中寻找 val1 和 val2 的最近公共祖先节点def find(self, root: 'TreeNode', val1: int, val2: int) -> 'TreeNode':if not root:return Noneif root.val > val2:# 当前节点太大,去左子树找return self.find(root.left, val1, val2)if root.val < val1:# 当前节点太小,去右子树找return self.find(root.right, val1, val2)# val1 <= root.val <= val2# 则当前节点就是最近公共祖先return root1650. 二叉树的最近公共祖先 III
再看最后一道最近公共祖先的题目吧,力扣第 1650 题「二叉树的最近公共祖先 III」,这次输入的二叉树节点比较特殊,包含指向父节点的指针。题目会给你输入一棵存在于二叉树中的两个节点 p 和 q,请你返回它们的最近公共祖先。函数签名如下:
class Node:def __init__(self):self.val = Noneself.left = Noneself.right = Noneself.parent = None# 函数签名
def lowestCommonAncestor(p: Node, q: Node) -> Node:由于节点中包含父节点的指针,所以二叉树的根节点就没必要输入了。
这道题其实不是公共祖先的问题,而是单链表相交的问题,你把 parent 指针想象成单链表的 next 指针,题目就变成了:
给你输入两个单链表的头结点 p 和 q,这两个单链表必然会相交,请你返回相交点。

【python】
class Solution:def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':# 施展链表双指针技巧a, b = p, qwhile a != b:# a 走一步,如果走到根节点,转到 q 节点a = q if a is None else a.parent# b 走一步,如果走到根节点,转到 p 节点return a3、总结
最近公共祖先问题,核心在于去理解p和q两个节点所处位置不同,引申出来的代码逻辑不同。
class Solution:def __init__(self):# 对于p,q 不确定有无得情况,需要额外加变量进行跟踪,并将find函数调整为后序遍历方式# 遇到p,q就更新这俩参数self.foundP = Falseself.foundQ = Falsedef lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':return self.find(root, p.val, q.val)# 在二叉树中寻找 val1 和 val2 的最近公共祖先节点def find(self, root: 'TreeNode', val1: int, val2: int) -> 'TreeNode':# 碰到叶子节点,返回None即可if not root:return None'''1、在前序位置遍历到目标值,不论是p还是q,直接返回该节点,其上层函数自有left或right做承接。2、即使给的不是val1和val2,而是一个list,依然只需判决该 root.val in list 即可返回root。3、若将此判决调到后序位置,则find方法会遍历所有节点,在不确定p,q是否存在的情况下用起来很方便。4、对于BST的最小公共祖先问题,只需明确p < q,root.val < p就去find右边,root.val > q就去find左边。'''if root.val == val1 or root.val == val2:# 如果遇到目标值,直接返回return root# find遍历便利的结果自然需要变量做承接,便于后续判决left = self.find(root.left, val1, val2)right = self.find(root.right, val1, val2)'''1、后续位置做left and right的判决,如果此节点left和right都存在,直接起一个截胡效果,不用继续向后遍历,直接确定该节点就是LCA并返回。2、即使给的不是val1和val2,而是一个list,即便某个节点的left and right各自只遍历到list中的一个值,放心地 return root, 因为自然会有上层函数通过这段代码进行“截胡”,依然能正确返回上层那个 left and right 都满足的节点。'''if left and right:# 当前节点是 LCA 节点return root'''1、当后序位置的 left and right判决迟迟未响应时,这行 return 代码做了最后的兜底。2、即使给的不是val1和val2,而是一个list,同理直接对该节点进行return,也是起一个兜底的效果。'''return left if left else right相关文章:

【算法思想·二叉树】最近公共祖先问题
本文参考labuladong算法笔记[拓展:最近公共祖先系列解题框架 | labuladong 的算法笔记] 0、引言 如果说笔试的时候经常遇到各种动归回溯这类稍有难度的题目,那么面试会倾向于一些比较经典的问题,难度不算大,而且也比较实用。 本…...

如何合并pdf文件,四款软件,三步搞定!
在数字化办公的浪潮中,PDF文档因其跨平台兼容性和安全性,成为了我们日常工作中不可或缺的一部分。然而,面对多个PDF文件需要整合成一个文件时,不少小伙伴可能会感到头疼。别担心,今天我们就来揭秘四款高效PDF合并软件&…...

仪表放大器AD620
AD623 是一款低功耗、高精度的仪表放大器,而不是轨到轨运算放大器。它的输入电压范围并不覆盖整个电源电压(轨到轨),但在单电源供电下可以处理接近地电位的输入信号。 AD620 和 AD623 都是仪表放大器,但它们在一些关键…...

【Qt网络编程】Tcp多线程并发服务器和客户端通信
目录 一、编写思路 1、服务器 (1)总体思路widget.c(主线程) (2)详细流程widget.c(主线程) (1)总体思路chat_thread.c(处理聊天逻辑线程&…...

SkyWalking 简介
SkyWalking是什么 skywalking是一个国产开源框架,2015年由吴晟开源 , 2017年加入Apache孵化器。skywalking是分布式系统的应用 程序性能监视工具,专为微服务、云原生架构和基于容器(Docker、K8s、Mesos)架构而设计。它是一款优秀的 APM(Application Performance Manag…...

语音合成(自然、非自然)
1.环境 Python 3.10.14 2.完成代码 2.1简陋版 import pyttsx3# 初始化tts引擎 engine pyttsx3.init()# 设置语音速度 rate engine.getProperty(rate) engine.setProperty(rate, rate - 50)# 设置语音音量 volume engine.getProperty(volume) engine.setProperty(volume, …...

redis简单使用与安装
redis redis 是什么 Redis 是一个开源的,使用 C 语言编写的,支持网络交互的,内存中的Key-Value 数据结构存储系统,支持多种语言,它可以用作数据库、缓存和消息中间件。 一、存储系统特性 内存存储与持久化 Redis 主要将数据存储在内存中,这…...

封装 WBXpopup 组件
这是Popup组件基于微博小程序,需要改变标签,以及一写方法 支持四个方向抽屉,以及中间弹出功能 // 用法 <template><wbx-view style"height: 100vh;"><!-- 对话框组件 --><wbx-view><wbx-text click&quo…...

【OJ刷题】双指针问题6
这里是阿川的博客,祝您变得更强 ✨ 个人主页:在线OJ的阿川 💖文章专栏:OJ刷题入门到进阶 🌏代码仓库: 写在开头 现在您看到的是我的结论或想法,但在这背后凝结了大量的思考、经验和讨论 目录 1…...

详解:Tensorflow、Pytorch、Keras(搭建自己的深度学习网络)
这是一个专门对Tensorflow、Pytorch、Keras三个主流DL框架的一个详解和对比分析 一、何为深度学习框架? 你可以理解为一个工具帮你构建一个深度学习网络,调用里面的各种方法就能自行构建任意层,diy你想要的DNN,而且任意指定学习…...

【CSS in Depth 2 精译_035】5.5 Grid 网格布局中的子网格布局(全新内容)
当前内容所在位置(可进入专栏查看其他译好的章节内容) 第一章 层叠、优先级与继承(已完结) 1.1 层叠1.2 继承1.3 特殊值1.4 简写属性1.5 CSS 渐进式增强技术1.6 本章小结 第二章 相对单位(已完结) 2.1 相对…...

Java是怎么处理死锁的
文章目录 避免死锁避免嵌套锁资源进行排序超时锁 检测死锁通过Java提供的API检查死锁情况jStack监控工具 Java 本身没有内置的机制自动处理死锁问题,但可以采取一些策略和技术来检测和避免死锁。 避免死锁 避免嵌套锁 尽可能减少嵌套锁操作,避免在一个…...

Effective Java 学习笔记 方法签名设计
目录 谨慎选择方法名称 不要过于追求提供便利的快捷方法 避免过长的参数列表 对于参数类型优先使用接口而不是类 对于boolean参数,要优先使用两个元素的枚举类型 本文接续前一篇文章聚焦Java方法签名的设计,方法签名包括了方法的输入和输出参数以及…...

毛利超70%、超70+智驾客户,这家AI数据训练服务商刚刚止亏
AI训练数据服务第一股海天瑞声终于迎来了“曙光”。 日前,海天瑞声发布2024年半年报显示,上半年其实现营收9242.63万,同比增长24.13%;实现净利润41.64 万元,不过同比去年同期的亏损1724.14万元,扭亏为盈。…...

本地部署高颜值某抑云音乐播放器Splayer并实现无公网IP远程听歌
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

图像压缩编码(4)--H.26x系列视频压缩编码_2
目录 H.261 视频编码标准 H.261的编码与解码 1) 帧内/帧间编码 2)运动补偿 3)量化 4)环路滤波器 5)缓存器 压缩数据的分层 数据复用结构 H.264的编码与解码 H.261 视频编码标准 实际应用时,要求有…...

JS渲染锻炼输入表单
前言 上篇文章为大家展现了好看的信息窗口,接下来我们跟着流程图看下一步 之前我们的带点击事件已经添加完毕,下一步就是当用户点击的时候,渲染锻炼形式,当然这是一个标签,可以提供给用户输入锻炼形式 实例 ● 我…...

proteus仿真学习(1)
一,创建工程 一般选择默认模式,不配置pcb文件 可以选用芯片型号也可以不选 不选则从零开始布局,没有初始最小系统。选用则有初始最小系统以及基础的main函数 本次学习使用从零开始,不配置固件 二,上手软件 1.在元件…...

决策树+随机森林模型实现足球大小球让球预测软件
文章目录 前言一、决策树是什么?二、数据收集与整理1.数据收集2.数据清洗3.特征选择 三、决策树构建3.1绘制训练数据图像3.2 训练决策树模型3.3 依据模型绘制决策树的决策边界3.4 树模型可视化 四、模型预测五、随机森林模型总结 前言 之前搞足球数据分析的时候&…...
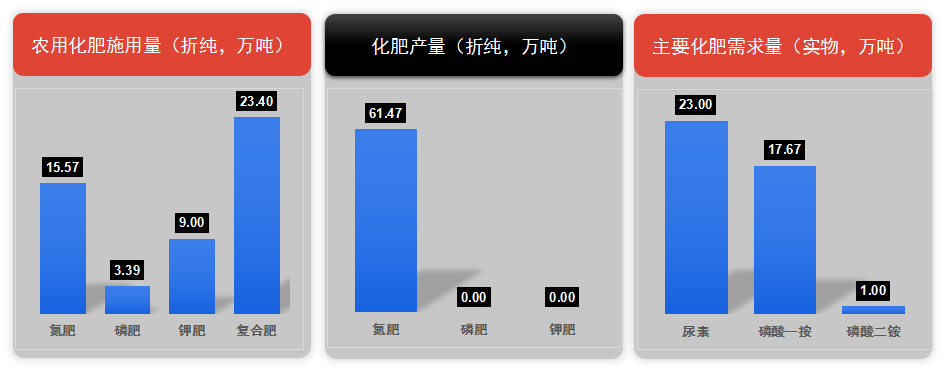
31省市农业地图大数据
1.北京市 谷类作物种植结构(万亩) 农作物种植结构(万亩) 2.天津市 谷类作物种植结构(万亩) 农作物种植结构(万亩) 3.黑龙江省 谷类作物种植结构(万亩) 农作物…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
