【C++】10道经典面试题带你玩转二叉树

🦄个人主页:修修修也

🎏所属专栏:C++

⚙️操作环境:Leetcode/牛客网

---

目录

一.根据二叉树创建字符串

二.二叉树的层序遍历

三.二叉树的层序遍历 II

四.二叉树的最近公共祖先

五.二叉搜索树与双向链表

六.从前序与中序遍历序列构造二叉树

七.从中序与后序遍历序列构造二叉树

八.二叉树的前序遍历(迭代算法)

九.二叉树的中序遍历(迭代算法)

十.二叉树的后序遍历(迭代算法)

结语

---

一.根据二叉树创建字符串

题目链接:

606. 根据二叉树创建字符串https://leetcode.cn/problems/construct-string-from-binary-tree/

---

题目描述:

        给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。

        空节点使用一对空括号对 "()" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

---

题目详情:

---

解题思路:

使用前序遍历遍历整颗树即可,但是要注意遍历根节点时不需要加括号,如果有子树,无论左子树有没有都要加括号,右子树有才加,没有就不加。具体细节见解题代码注释。

---

解题代码:

class Solution 
{
public:string tree2str(TreeNode* root) {if(root){//先遍历根节点string ret = to_string(root->val);//不用to_string用+48会遇到负数//只要左或右不为空,就进去执行,否则是叶子,直接返回if(root->left || root->right){//再遍历左子树//因为左树为空也必须有"()",所以我们不用判断直接执行ret += ( '(' + tree2str(root->left) + ')' );//最后遍历右子树//因为右树为空没有"()",所以我们需要判断一下if(root->right){ret += ( '(' + tree2str(root->right) + ')' );}}return ret;}else{return "";}}
};

提交运行:

---

二.二叉树的层序遍历

题目链接:

102. 二叉树的层序遍历https://leetcode.cn/problems/binary-tree-level-order-traversal/

---

题目描述:

        给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

---

题目详情:

---

解题思路:

        思路就是因为我们要返回的是二维数组,所以必须要记录下结点是哪一层的.有两种方法可以使用:

1. 一种是用两个队列,第一个队列先入第一层的结点,然后出第一个队列结点时将下一层结点存入第二个队列中,出第二个队列时再把下一层结点存入第一个队列中,边出边将数据存入相应层的vector里,直到两个队列中的结点出完代表二叉树层序遍历结束.
2. 另一种是使用一个队列,然后使用一个levelSize变量来记录下上一层结点出的时候入了多少个,下一层就循环多少次将数据放入vector里,直到队列出空,代表二叉树遍历结束.

---

解题代码:

class Solution 
{
public:vector<vector<int>> levelOrder(TreeNode* root) {//因为要返回的是二维数组,所以必须双队列或者用一个变量控制levelSize//我们就是一层一层入,一层一层出,一层入完统计有多少个,出下层就出多少个queue<TreeNode*> q;vector<vector<int>> vv;int levelSize=0;if(root){q.push(root);levelSize=1;}while(!q.empty())//while循环一次就是一层{vector<int> v;for(int i=0;i<levelSize;i++){TreeNode*front=q.front();q.pop();v.push_back(front->val);if(front->left!=nullptr){q.push(front->left);}if(front->right!=nullptr){q.push(front->right);}}vv.push_back(v);levelSize=q.size();}return vv;}
};

提交运行:

---

三.二叉树的层序遍历 II

题目链接:

107. 二叉树的层序遍历 IIhttps://leetcode.cn/problems/binary-tree-level-order-traversal-ii/

---

题目描述:

        给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

---

题目详情:

---

解题思路:

需要倒着层序遍历二叉树,我们可以先正着遍历,然后再把存放数据的二维数组逐层逆置一下就可以了,正着层序遍历的思路和代码和上题一模一样这里就不赘述了.

---

解题代码:

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {//先正着层序遍历,后面再逆置一下就行//因为要返回的是二维数组,所以必须双队列或者用一个变量控制levelSize//我们就是一层一层入,一层一层出,一层入完统计有多少个,出下层就出多少个queue<TreeNode*> q;vector<vector<int>> vv;int levelSize=0;if(root){q.push(root);levelSize=1;}while(!q.empty())//while循环一次就是一层{vector<int> v;for(int i=0;i<levelSize;i++){TreeNode*front=q.front();q.pop();v.push_back(front->val);if(front->left!=nullptr){q.push(front->left);}if(front->right!=nullptr){q.push(front->right);}}vv.push_back(v);levelSize=q.size();}//要倒着的层序遍历,那我们先正着存,再逆置一下数组就行vv.vector<vector<int>> vvr;for(int i=vv.size()-1;i>=0;i--){vvr.push_back(vv[i]);}return vvr;}
};

提交运行:

---

四.二叉树的最近公共祖先

题目链接:

236. 二叉树的最近公共祖先https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/

---

题目描述:

        给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

        百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

---

题目详情:

---

解题思路:

方法一:暴力查找

借用搜索二叉树的查找思路,重点是向下查找时,找到它们最开始"分叉"的那个结点,就是最近祖先结点,图示如下:           因此我们只需要递归找到从这个结点开始两个结点一个位于它左子树一个位于它右子树的那个结点,就是最近共同祖先,这种思路简单,但是时间复杂度较高,在O(nlogn)~O(n^2)之间.

方法二:栈存路径

        方法二的思路是我在查找p,q结点的时候顺带用两个栈把它们的路径存下来,然后找到栈的最顶上的相等结点即可,该思路时间复杂度较低,为O(n),思路图示如下:

---

解题代码:

方法一:

class Solution 
{
public:bool Find(TreeNode* root, TreeNode* x){if(root==nullptr){return false;}return root==x || Find(root->left,x)||Find(root->right,x);}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == nullptr)   //这种是找不到的情况,可以不写,因为题干说两个结点一定存在{return nullptr;}if(root == p || root == q)  //如果p/q就是root了,那其公共祖先一定是它本身{return root;}//开始确定p,q对于root的位置bool pInLeft,pInRight,qInLeft,qInRight;pInLeft=Find(root->left,p);   //pInLeft记录p在root的左子树存在情况pInRight=!pInLeft;    //pInright记录p在root的右子树存在情况qInLeft=Find(root->left,q);    //qInLeft记录q在root的左子树存在情况qInRight=!qInLeft;      //qInright记录q在root的右子树存在情况if(pInLeft && qInLeft)  //如果p,q都在root的左子树,那向左继续找{return lowestCommonAncestor(root->left,p,q);}else if(pInRight && qInRight)  //如果p,q都在root的右子树,那向右继续找{return lowestCommonAncestor(root->right,p,q);}else        //如果p,q一个在root的左子树,一个在root的右子树,那root就是分叉点,就是最近共同祖先{return root;}}
};

提交运行:

方法二:

class Solution 
{
public:bool FindPath(TreeNode* root,TreeNode* x, stack<TreeNode*>& path){if(root == nullptr){return false;}path.push(root);if(root==x)return true;if(FindPath(root->left,x,path))return true;if(FindPath(root->right,x,path))return true;path.pop();return false;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {stack<TreeNode*> pPath,qPath;FindPath(root,p,pPath);FindPath(root,q,qPath);while(pPath.size()>qPath.size()){pPath.pop();}while(pPath.size()<qPath.size()){qPath.pop();}while(pPath.top()!=qPath.top()){pPath.pop();qPath.pop();}return pPath.top();}
};

提交运行:

---

五.二叉搜索树与双向链表

题目链接:

JZ36 二叉搜索树与双向链表https://www.nowcoder.com/practice/947f6eb80d944a84850b0538bf0ec3a5?tpId=13&&tqId=11179&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking

---

题目描述:

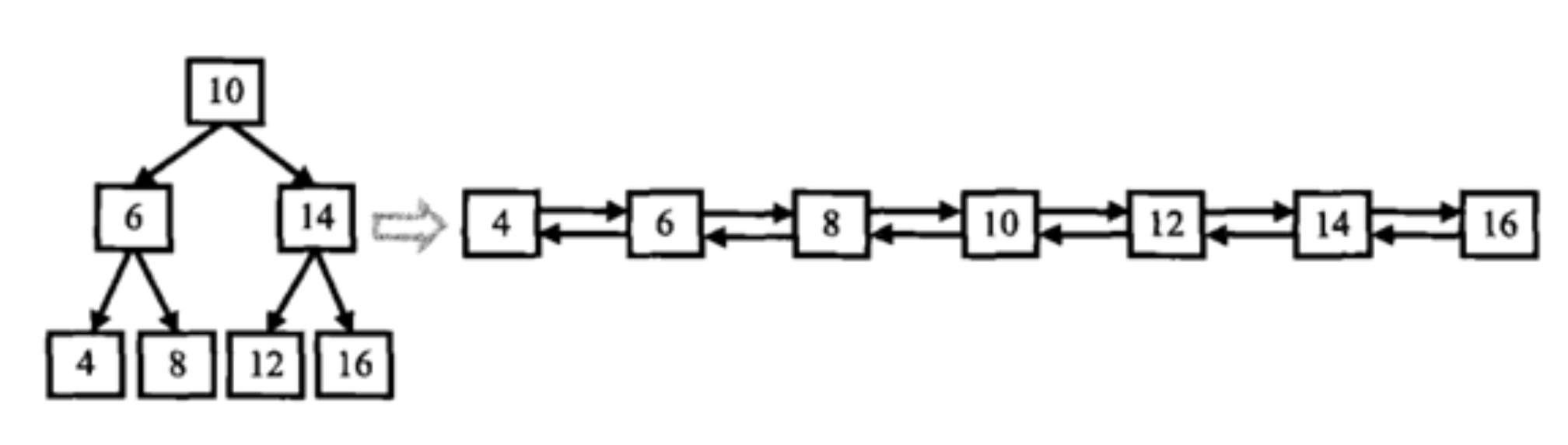
        输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

        数据范围：输入二叉树的节点数 0≤n≤10000≤n≤1000，二叉树中每个节点的值                         0≤val≤10000≤val≤1000
        要求：空间复杂度O(1)O(1)（即在原树上操作），时间复杂度 O(n)O(n)

注意:

1. 要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2. 返回链表中的第一个节点的指针
3. 函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构
4. 你不用输出双向链表，程序会根据你的返回值自动打印输出

---

题目详情:

---

解题思路:

使用中序递归遍历的逻辑函数,函数包含两个参数,一个表示当前结点,一个表示上一层递归的结点prev。因为搜索二叉树中序遍历的结点顺序就是有序的,因此只要在遍历时顺便将这些结点前后链接起来即可.具体链接时,因为我们传给函数的参数是当前结点和上一结点,所以我们链接时,就将当前结点的左指针连接上上一结点,然后将上一结点的右指针连接上当前结点即可,更多细节见解题代码注释.

---

解题代码:

class Solution 
{
public://中序遍历void InOrder(TreeNode* cur,TreeNode*& prev)//传引用就不怕改形参不影响实参了{if (cur == nullptr)return;//中序:左InOrder(cur->left,prev);//链接左指针使其连接到上一个递归的结点cur->left=prev;//链接前一个的右指针使其指向我自己if(prev)prev->right=cur;prev=cur;//中序:右InOrder(cur->right,prev);}TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode* prev = nullptr;InOrder(pRootOfTree,prev);//找最左结点,一直往左走就行,但小心一开始就为空的情况TreeNode* cur=pRootOfTree;while(cur && cur->left){cur=cur->left;}return cur;}
};

提交运行:

---

六.从前序与中序遍历序列构造二叉树

题目链接:

105. 从前序与中序遍历序列构造二叉树https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

---

题目描述:

        给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

---

题目详情:

---

解题思路:

        将前序结点数组按照从前向后的顺序遍历, 将每一个结点都看作根，然后去中序根据这个根来划分左右子树。中序数组中,左子树一定在根的左边,右子树一定在根的右边, 到下一个结点时,就更新下一个结点的子树范围。

        如果这个范围不存在,那表明这个树没有子树,直接链接nullptr即可。

        图示如下:

---

解题代码:

class Solution 
{
public:TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei, int inbegin, int inend) {if(inbegin > inend)return nullptr;TreeNode* root = new TreeNode(preorder[prei]);int rooti = inbegin;while(rooti <= inend){if(preorder[prei] == inorder[rooti])break;++rooti;}//根据中序将数组分为三段//      左子树          根          右子树//[inbegin,rooti-1]  [rooti]  [rooti+1,inend]++prei;root->left=_buildTree(preorder,inorder,prei,inbegin,rooti-1);root->right=_buildTree(preorder,inorder,prei,rooti+1,inend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int prei=0;return _buildTree(preorder,inorder,prei,0,inorder.size()-1);}
};

提交运行:

---

七.从中序与后序遍历序列构造二叉树

题目链接:

106. 从中序与后序遍历序列构造二叉树

---

题目描述:

        给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

---

题目详情:

---

解题思路:

本题与上一题思路相似,只是后序数组要从后向前遍历构造二叉树,则后序数组向前访问到的结点的顺序是先根再右再左,只有这一点需要特别注意,其余和上一题没有什么区别.图示如下:

---

解题代码:

class Solution 
{
public:TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& prei, int inbegin, int inend) {if(inbegin > inend)return nullptr;TreeNode* root = new TreeNode(postorder[prei]);int rooti = inbegin;while(rooti <= inend){if(postorder[prei] == inorder[rooti])break;++rooti;}//根据中序将数组分为三段//      左子树          根          右子树//[inbegin,rooti-1]  [rooti]  [rooti+1,inend]--prei;//后序从后向前遍历时是先根再右再左!root->right=_buildTree(inorder,postorder,prei,rooti+1,inend);root->left=_buildTree(inorder,postorder,prei,inbegin,rooti-1);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int prei=inorder.size()-1;return _buildTree(inorder,postorder,prei,0,inorder.size()-1);}
};

提交运行:

---

八.二叉树的前序遍历(迭代算法)

题目链接:

144. 二叉树的前序遍历https://leetcode.cn/problems/binary-tree-preorder-traversal/

---

题目描述:

        给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

---

题目详情:

---

解题思路:

        本题的迭代算法即不使用递归来完成树的前序遍历,我们还是借助栈来完成,具体思路是,先访问左路结点,并将其存入vector,入栈,当左路走到底时,我们先将该根节点pop出栈, 再访问栈顶结点的右路。

        当我们来到右路时,把右路再当成一个新的根节点,同样先访问左路,并将其存入vector,入栈,当左路走到底时,我们先将该根节点pop出栈, 再访问栈顶结点的右路,就这样不断循环, 直到栈中所有元素pop完,代表这颗树已经全部按照先序存入vector中了。

        思路图示如下:

---

解题代码:

class Solution 
{
public:vector<int> preorderTraversal(TreeNode* root){stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){//访问左路结点,左路结点入栈,后续依次访问左路节点的右子树while(cur){v.push_back(cur->val);st.push(cur);cur=cur->left;}//依次访问左路节点的右子树TreeNode* top = st.top();st.pop();cur = top->right;}return v;}
};

提交运行:

---

九.二叉树的中序遍历(迭代算法)

题目链接:

94. 二叉树的中序遍历https://leetcode.cn/problems/binary-tree-inorder-traversal/

---

题目描述:

        给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

---

题目详情:

---

解题思路:

中序和先序的区别就是,先序是访问左子树前就将数据push进vector了,而中序遍历时我们是先将左子树访问完,再开始入vector.同样是借助栈来完成,区别仅在于向vector里push的时机.

---

解题代码:

class Solution 
{
public:vector<int> inorderTraversal(TreeNode* root) {stack<TreeNode*> st;vector<int> v;TreeNode* cur = root;while(cur || !st.empty()){//访问左路结点,左路结点入栈,后续依次访问左路节点的右子树while(cur){st.push(cur);cur=cur->left;}//依次访问左路节点和其右子树TreeNode* top = st.top();st.pop();v.push_back(top->val);cur = top->right;}return v;}
};

提交运行:

---

十.二叉树的后序遍历(迭代算法)

题目链接:

145. 二叉树的后序遍历https://leetcode.cn/problems/binary-tree-postorder-traversal/

---

题目描述:

        给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

---

题目详情:

---

解题思路:

        对于后序遍历而言,我们要先了解一个概念:

        因此我们后序遍历时插入vector的时机就是在上一次访问到是它的右节点时表示是最后一次访问了的时候,才将其Push进vector中,这样得到的vector就是按照后序遍历的结果了。

---

解题代码:

class Solution 
{
public:vector<int> postorderTraversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* prev =nullptr;TreeNode* cur = root;vector<int> v;while(cur || !st.empty()){while(cur){st.push(cur);cur=cur->left;}TreeNode* top = st.top();//一个结点右子树为空,或者上一个访问的结点是右子树,那么说明是最后一次经过了//就可以访问了if(top->right == nullptr || top->right == prev){prev = top;v.push_back(top->val);st.pop();}else{cur = top->right;}}return v;}
};

提交运行:

---

结语

        希望通过上面的题目能使大家对二叉树的理解以及运用能够更上一层楼,欢迎大佬们留言或私信与我交流.学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!

相关文章推荐

【数据结构】什么是二叉搜索(排序)树?

【数据结构】C语言实现链式二叉树(附完整运行代码)

【C++】模拟实现priority_queue(优先级队列)

【C++】模拟实现queue

【C++】模拟实现stack

【C++】模拟实现list

【C++】模拟实现vector

【C++】模拟实现string类

【C++】构建第一个C++类:Date类

【C++】类的六大默认成员函数及其特性(万字详解)

【C++】什么是类与对象?

---