树上差分+lca 黑暗的锁链
//** 太久不写了,感觉很难受。。。比赛最近打得也不好,课内任务又重,还要忙着做项目。何去何从。
今天又写了一题,用了树上差分的知识。下面来整理整理。
1.首先让我们学一下lca(最小公共父节点)
我用的是倍增来求的。总共其实就是两步:dfs打ST表预处理每个点的上面节点 lca求两点最小公共节点。lca里用了类似dp的思想。首先要知道dep[i][j]表示 i点向上跳1<<j个点后到达的点。然后想出递推关系式:dep[i][j]=dep[dep[i][j-1]][j-1]。用dfs来递推实现即可。
lca的实现其实就是 1.先将两个点化为同一层的点
2.寻找那一层的父节点是一样的
下面来看一下代码~
//倍增法求最近公共祖先LCA
#include<iostream>
using namespace std;int n,m;struct EDGE{int u,v,l;EDGE* ne;
}edge[100010];struct NODE{EDGE* fir;
}node[100010];int tot;
void my_build(int u,int v,int l){edge[tot].u=u;edge[tot].v=v;edge[tot].l=l;edge[tot].ne=node[u].fir;node[u].fir=&edge[tot];tot++;
}int ce[100010],dep[100010][20];//ce表示每个点的层数 dep[i][j]表示从第i个点向上走 1<<j (2^j) 个点到达的点位置;
/*
dep[i][j]=dep[dep[i][j-1]][j-1]; 递推关系式
*/
void dfs(int u,int f){//打ST表 复杂度:nlognce[u]=ce[f]+1;dep[u][0]=f;for(int i=1;i<=19;i++){dep[u][i]=dep[dep[u][i-1]][i-1];//类似dp}EDGE* i=node[u].fir;while(i!=NULL){if(i->v==f){i=i->ne;continue;}dfs(i->v,u);i=i->ne;}
}int lca(int u,int v){ //LCA 复杂度:lognif(ce[u]<ce[v]){swap(u,v);}for(int i=19;i>=0;i--){if(ce[dep[u][i]]>=ce[v]){u=dep[u][i];}}if(u==v)return u;for(int i=19;i>=0;i--){if(dep[u][i]!=dep[v][i]){u=dep[u][i];v=dep[v][i];}}return dep[u][0];
}int main()
{cin>>n>>m;//建边之类...略;return 0;
}
2.树上差分
树上差分分两种:1.给点差分 2.给边差分
对应着两种不一样的题意:给点操作还是给边操作。
给点操作很好理解,就是每个点加加减减。但如果要给边操作,我们无法轻松表示边呐,so我们就以点代边,每个点表示其与父节点连接的边。
看一下操纵吧~
//给每个点做差分:例如 给u->v路径上所有点+1:sum[u]++; sum[v]++; sum[lca]-=2;
//给边做差分->归结到给点做差分:sum[u]++; sum[v]++; sum[lca]-=1; sum[fa[lca]]-=1;//差分数组求前缀和:
void my_add(int u,int fa){//差分数组求前缀和;EDGE* i=node[u].fir;while(i!=NULL){if(i->v==fa){i=i->ne;continue;}dfs(i->v,u);sum[u]+=sum[i->v];i=i->ne;}
}//差分数组:(以给边差分为例)
while(m--){cin>>u>>v;int l=lca(u,v);sum[u]++;sum[v]++;sum[l]--;sum[dep[l][0]]--;
}
3.看题目
问题 : 黑暗的锁链
题目描述
传说中的暗之连锁被人们称为Dark。Dark是人类内心的黑暗的产物,古今中外的勇者们都试图打倒它。经过研究,你发现Dark呈现无向图的结构,图中有N个节点和两类边,一类边被称为主要边,而另一类被称为附加边。Dark有N–1条主要边,并且Dark的任意两个节点之间都存在一条只由主要边构成的路径。另外,Dark还有M条附加边。
你的任务是把Dark斩为不连通的两部分。一开始Dark的附加边都处于无敌状态,你只能选择一条主要边切断。一旦你切断了一条主要边,Dark就会进入防御模式,主要边会变为无敌的而附加边可以被切断。但是你的能力只能再切断Dark的一条附加边。现在你想要知道,一共有多少种方案可以击败Dark。注意,就算你第一步切断主要边之后就已经把Dark斩为两截,你也需要切断一条附加边才算击败了Dark。
输入
第一行包含两个整数N和M。
之后N–1行,每行包括两个整数A和B,表示A和B之间有一条主要边。
之后M行以同样的格式给出附加边。
输出
输出一个整数表示答案。
样例输入 Copy
4 1 1 2 2 3 1 4 3 4
样例输出 Copy
3
提示
对于20%的数据,N≤100,M≤100。
对于100%的数据,N≤100000,M≤200000。数据保证答案不超过231–1。
这题用的就是树上差分+lca。而且是面向边的树上差分(因为是要切边)。
看代码~
#include<iostream>
using namespace std;
#define int long long int n,m;struct EDGE{int u,v;EDGE* ne;
}edge[1000010];struct NODE{EDGE* fir;
}node[1000010];int tot;
void my_build(int u,int v){edge[tot].u=u;edge[tot].v=v;edge[tot].ne=node[u].fir;node[u].fir=&edge[tot];tot++;
}int dep[100010][20],ce[1000010];
void dfs(int u,int fa){ce[u]=ce[fa]+1;EDGE* i=node[u].fir;dep[u][0]=fa;for(int j=1;j<20;j++){dep[u][j]=dep[dep[u][j-1]][j-1];}while(i!=NULL){if(i->v==fa){i=i->ne;continue;}dfs(i->v,u);i=i->ne;}
}int lca(int u,int v){if(ce[u]<ce[v]){swap(u,v);}for(int i=19;i>=0;i--){if(ce[dep[u][i]]>=ce[v]){u=dep[u][i];}}if(u==v)return u;for(int i=19;i>=0;i--){if(dep[u][i]!=dep[v][i]){u=dep[u][i];v=dep[v][i];}}return dep[u][0];
}int sum[1000010];
void my_add(int u,int fa){EDGE* i=node[u].fir;while(i!=NULL){if(i->v==fa){i=i->ne;continue;}my_add(i->v,u);//注意不是dfs(找了很久的bug...)sum[u]+=sum[i->v];i=i->ne;}
}signed main()
{cin>>n>>m;int u,v;for(int i=1;i<=n-1;i++){cin>>u>>v;my_build(u,v);my_build(v,u);}dfs(1,0);for(int i=1;i<=m;i++){cin>>u>>v;int l=lca(u,v);sum[u]++;sum[v]++;sum[l]-=2;}my_add(1,0);int ans=0;for(int i=2;i<=n;i++){if(sum[i]==0){ans+=m;//注意是+m!!!}else if(sum[i]==1){ans++;}}cout<<ans;return 0;
}相关文章:

树上差分+lca 黑暗的锁链
//** 太久不写了,感觉很难受。。。比赛最近打得也不好,课内任务又重,还要忙着做项目。何去何从。 今天又写了一题,用了树上差分的知识。下面来整理整理。 1.首先让我们学一下lca(最小公共父节点) 我用的…...

opencv4.5.5 GPU版本编译
一、安装环境 1、opencv4.5.5 下载地址:https://github.com/opencv/opencv/archive/refs/tags/4.5.5.ziphttps://gitee.com/mirrors/opencv/tree/4.5.0 2、opencv-contrib4.5.5 下载地址:https://github.com/opencv/opencv_contrib/archive/refs/tags/4…...
线性跟踪微分器TD详细测试(Simulink 算法框图+SCL完整源代码)
1、ADRC线性跟踪微分器 ADRC线性跟踪微分器(ST+SCL语言)_adrc算法在博途编程中scl语言-CSDN博客文章浏览阅读784次。本文介绍了ADRC线性跟踪微分器的算法和源代码,包括在SMART PLC和H5U平台上的实现。文章提供了ST和SCL语言的详细代码,并讨论了跟踪微分器在自动控制中的作用…...
LabVIEW闪退
LabVIEW闪退或无法启动可能由多个原因引起,特别是在使用了一段时间后突然发生的问题。重启电脑后 LabVIEW 和所有 NI 软件都无法打开,甚至在卸载和重装时也没有反应。这种情况通常与系统环境、软件冲突或 NI 软件组件的损坏有关。 1. 检查系统和软件冲突…...

【WPF】03 动态生成控件
说明 今天记录一篇关于动态生成控件的方法,也是反复查了一些资料,逐步完善成自己需要的方法,感觉还是比较好用的。通过这个需求,在网上也找了一些资料,发现了一个开源图形UI组件HandyControl,觉得比较好&a…...

调试LTE模块碰到的4字节对齐问题
在调试LTE模块,有两个模块,碰到两种4字节对齐问题,其错误提示都是类似如下的内容: DWC_OTG: dwc_otg_hcd_urb_enqueue urb->transfer_buffer address not align to 4-byte 0xee419e8e 都是USB控制器处理的数据时需要4字节对齐…...
一篇讲完HTML核心内容
一、HTML 1、 HTML概念 网页,是网站中的一个页面,通常是网页是构成网站的基本元素,是承载各种网站应用的平台。通俗的说,网站就是由网页组成的。通常我们看到的网页都是以htm或html后缀结尾的文件,俗称 HTML文件。 2、…...

2024icpc(Ⅱ)网络赛补题 G
2024icpc(Ⅱ)网络赛补题 G 题目链接:The 2024 ICPC Asia EC Regionals Online Contest (II) G、Game 题意: 给定Alice和Bob的每一轮的概率 p 0 , p 1 p_0, p_1 p0,p1 给定Alice和Bob的初始数字 x , y x,y x,y。 对于每一轮: 如果Al…...

AIGC时代!AI的“iPhone时刻”与投资机遇
AIGC时代!AI的“iPhone时刻”与投资机遇 前言AI的“iPhone时刻”与投资机遇 前言 AIGC,也就是人工智能生成内容,它就像是一股汹涌的浪潮,席卷了整个科技世界。它的出现,让我们看到了人工智能的无限潜力,也…...
Kubernetes调度单位Pod
Kubernetes调度单位Pod 1 Pod简介 不直接操作容器container。 一个 pod 可包含一或多个容器(container),它们共享一个 namespace(用户,网络,存储等),其中进程之间通过 localhost 本地…...

C语言指针篇
要想学好C语言,作为灵魂的指针那是必须要掌握的,而要想搞定指针,就不得不讲一下内存和地址之间的关系 内存和地址 计算机上的CPU(中央处理器)在处理数据的时候,需要的数据是在内存中读取的,处…...

Unity 使用Editor工具查找 Prefab 中的指定脚本
在 Unity 项目中,随着项目规模的扩大和 Prefab 数量的增加,管理和定位 Prefab 中的脚本变得更加复杂。为了提高开发效率,所以需要编写一个自定义的 Unity Editor 工具,帮助查找某个 Prefab 中是否使用了指定的脚本。本文将介绍如何…...

Frida-JSAPI:Interceptor使用
拦截器 Interceptor.attach(target, callbacks[, data]) 参数分析 target :target是一个NativePointer,用于指定想要拦截的函数的地址。callbacks :参数是一个包含一个或多个回调函数的对象。 onEnter(args) 回调函数,接收一个参…...

【深度学习】(3)--损失函数
文章目录 损失函数一、L1Loss损失函数1. 定义2. 优缺点3. 应用 二、NLLLoss损失函数1. 定义与原理2. 优点与注意3. 应用 三、MSELoss损失函数1. 定义与原理2. 优点与注意3. 应用 四、BCELoss损失函数1. 定义与原理2. 优点与注意3. 应用 五、CrossEntropyLoss损失函数1. 定义与原…...
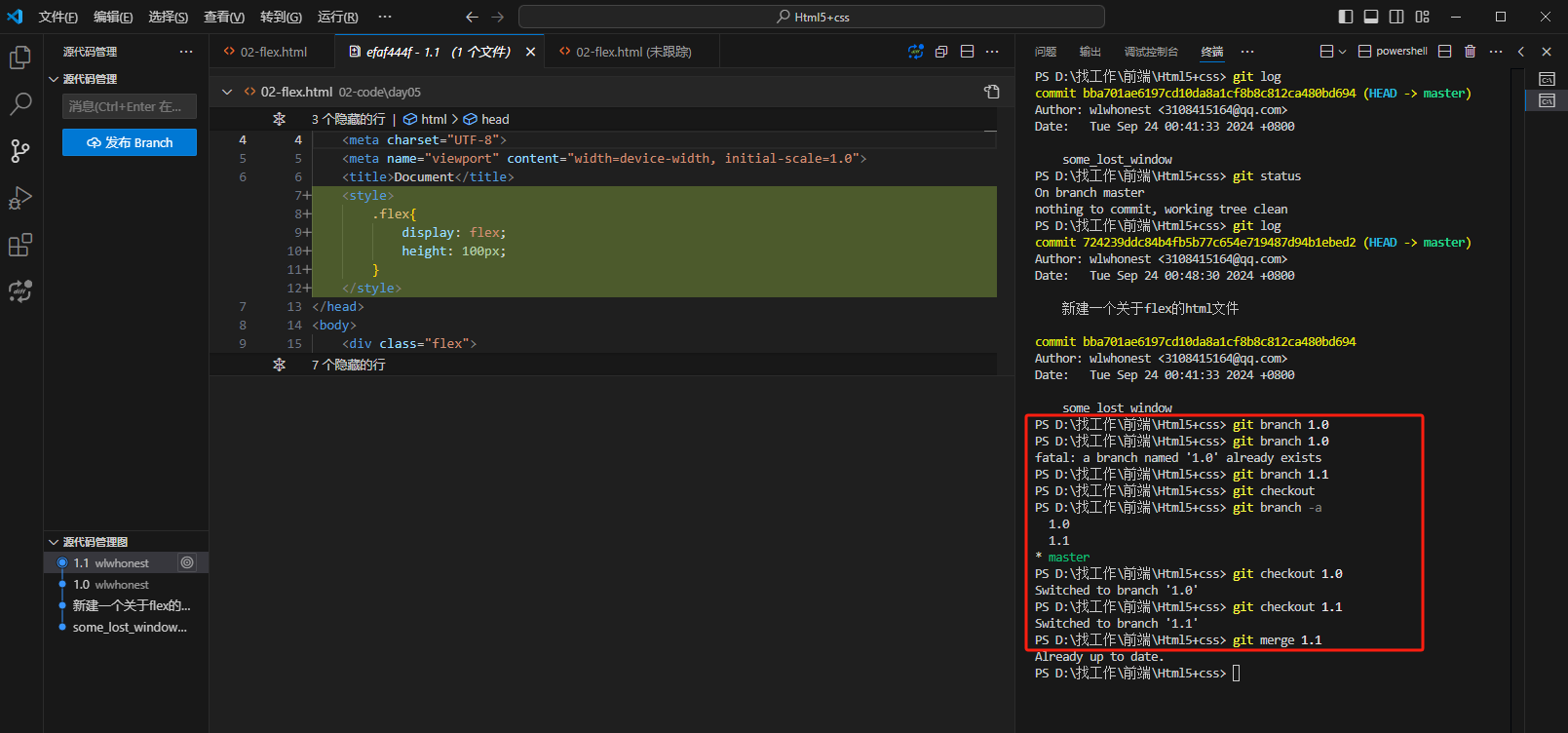
git学习报告
文章目录 git学习报告如何配置vscode终端安装PowerShell安装 Microsoft.Powershell.Preview使用 git的使用关于团队合作 git指令本地命令:云端指令 git学习报告 如何配置vscode 安装powershell调教window终端,使其像Linux一样,通过Linux命令…...

Spring MVC的应用
目录 1、创建项目与maven坐标配置 2、核心配置 3、启动项目测试 4、不同请求参数在controller的配置 4.1 servlet API 4.2 简单类型 4.3 pojo类型 4.4 日期类型 4.5 restful风格4种操作类型 4.5.1 GET:获取资源 4.5.2 POST:新建资源 4.5.3 P…...

JavaEE: 深入探索TCP网络编程的奇妙世界(六)
文章目录 TCP核心机制TCP核心机制九: 面向字节流TCP核心机制十: 异常处理 小小的补充(URG 和 PSH)~TCP小结TCP/UDP 对比用UDP实现可靠传输(经典面试题) 结尾 TCP核心机制 上一篇文章JavaEE: 深入探索TCP网络编程的奇妙世界(五) 书接上文~ TCP核心机制九: 面向字节流 TCP是面…...

探秘 Web Bluetooth API:连接蓝牙设备的新利器
引言 随着物联网技术的快速发展,蓝牙设备在日常生活中扮演着越来越重要的角色。而在 Web 开发领域,Web Bluetooth API 的出现为我们提供了一种全新的方式来连接和控制蓝牙设备。本文将深入探讨 Web Bluetooth API 的使用方法和原理,帮助开发…...

Kubernetes Pod调度基础(kubernetes)
实验环境依旧是k8s快照,拉取本次实验所需的镜像文件; 然后在master节点上传已经编写好的yaml文件; 然后同步会话,导入镜像; pod控制器: 标签选择器--》标签: 标签: 在Kubernetes&…...

Angular由一个bug说起之十:npm Unsupported engine
我们在用npm下载包的时候,有时候会碰到这样的提示 这是npm的警告,说我们使用的nodejs版本与下载的包所要求的nodejs版本不一致。 这是因为有些包它对nodejs的版本有要求,然后就会在package.json文件里的engines字段里声明它所要求的nodejs版本…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
