使用Python实现图形学曲线和曲面的NURBS算法
目录
- 使用Python实现图形学曲线和曲面的NURBS算法
- 引言
- NURBS曲线的数学原理
- 1. NURBS曲线定义
- 2. 权重的作用
- NURBS曲线的Python实现
- 1. 类结构设计
- 2. 代码实现
- 3. 代码详解
- 使用示例
- NURBS曲面的扩展
- NURBS曲面类实现
- 总结
使用Python实现图形学曲线和曲面的NURBS算法
引言
NURBS(Non-Uniform Rational B-Splines,非均匀有理B样条)是一种广泛应用于计算机图形学、CAD、动画设计和3D建模的数学表示方法。它是B样条(B-spline)的推广,能够表示直线、圆弧、椭圆以及更复杂的自由曲线和曲面。NURBS通过增加权重,赋予了控制点不同的影响力,从而能够精确表示圆形等几何形状。
本文将介绍NURBS曲线和曲面的基本原理,并使用Python面向对象的思想实现NURBS算法。
NURBS曲线的数学原理
1. NURBS曲线定义
NURBS曲线由控制点、权重和节点向量定义。给定 n + 1 n+1 n+1 个控制点 P 0 , P 1 , . . . , P n P_0, P_1, ..., P_n P0,P1,...,Pn,每个控制点对应一个权重 w 0 , w 1 , . . . , w n w_0, w_1, ..., w_n w0,w1,...,wn,NURBS曲线在参数 t t t 处的点 C ( t ) C(t) C(t) 的表达式为:
C ( t ) = ∑ i = 0 n N i , p ( t ) w i P i ∑ i = 0 n N i , p ( t ) w i C(t) = \frac{\sum_{i=0}^{n} N_{i,p}(t) w_i P_i}{\sum_{i=0}^{n} N_{i,p}(t) w_i} C(t)=∑i=0nNi,p(t)wi∑i=0nNi,p(t)wiPi
其中:
- N i , p ( t ) N_{i,p}(t) Ni,p(t) 是B样条基函数,和B样条曲线的定义一致。
- w i w_i wi 是控制点的权重,控制点对曲线的影响力大小。
- 节点向量 t t t 决定参数空间的分布。
2. 权重的作用
权重 w i w_i wi 决定了每个控制点对曲线的影响力。若所有权重相等,则NURBS曲线退化为普通的B样条曲线;而如果控制点的某些权重远大于其他权重,则这些控制点对曲线形状的影响力会更大。
NURBS曲线的Python实现
1. 类结构设计
我们将设计以下几个类:
Point2D:表示二维平面上的点。NURBSCurve:用于计算和绘制NURBS曲线的类。
2. 代码实现
import numpy as np# 定义二维点类
class Point2D:def __init__(self, x, y):self.x = xself.y = ydef __repr__(self):return f"({self.x}, {self.y})"# 定义NURBS曲线类
class NURBSCurve:def __init__(self, control_points, weights, degree, knot_vector=None):"""初始化NURBS曲线:param control_points: 控制点的列表,每个控制点是一个 Point2D 对象:param weights: 控制点的权重列表:param degree: NURBS的阶数(degree):param knot_vector: 节点向量,若为None,则使用均匀节点向量"""self.control_points = control_pointsself.weights = weightsself.degree = degreeself.num_control_points = len(control_points)# 生成均匀节点向量if knot_vector is None:self.knot_vector = self._generate_uniform_knot_vector()else:self.knot_vector = knot_vectordef _generate_uniform_knot_vector(self):"""生成均匀的节点向量:return: 均匀节点向量"""n = self.num_control_points - 1p = self.degreereturn [0] * (p + 1) + list(range(1, n - p + 1)) + [n - p + 1] * (p + 1)def _basis_function(self, i, k, t):"""计算B样条基函数:param i: 控制点索引:param k: 当前阶数:param t: 参数值:return: 基函数值"""if k == 0:return 1.0 if self.knot_vector[i] <= t < self.knot_vector[i+1] else 0.0else:# 计算两个部分coef1 = 0.0if self.knot_vector[i+k] != self.knot_vector[i]:coef1 = (t - self.knot_vector[i]) / (self.knot_vector[i+k] - self.knot_vector[i]) * self._basis_function(i, k-1, t)coef2 = 0.0if self.knot_vector[i+k+1] != self.knot_vector[i+1]:coef2 = (self.knot_vector[i+k+1] - t) / (self.knot_vector[i+k+1] - self.knot_vector[i+1]) * self._basis_function(i+1, k-1, t)return coef1 + coef2def calculate_point(self, t):"""计算曲线在参数t处的点:param t: 参数值 t, 范围 [0, 1]:return: 返回曲线在 t 处的 Point2D 点"""numerator_x = 0.0numerator_y = 0.0denominator = 0.0for i in range(self.num_control_points):b = self._basis_function(i, self.degree, t)numerator_x += b * self.weights[i] * self.control_points[i].xnumerator_y += b * self.weights[i] * self.control_points[i].ydenominator += b * self.weights[i]return Point2D(numerator_x / denominator, numerator_y / denominator)def generate_curve_points(self, num_points=100):"""生成NURBS曲线上的点:param num_points: 生成的曲线上点的数量:return: 返回点列表,表示NURBS曲线"""curve_points = []for t in np.linspace(self.knot_vector[self.degree], self.knot_vector[-self.degree-1], num_points):curve_points.append(self.calculate_point(t))return curve_points# 使用示例
if __name__ == "__main__":# 定义控制点control_points = [Point2D(0, 0), Point2D(1, 2), Point2D(3, 3), Point2D(4, 0)]# 定义权重weights = [1, 0.5, 0.5, 1]# 创建NURBS曲线对象,阶数为3(三次NURBS)nurbs_curve = NURBSCurve(control_points, weights, degree=3)# 生成并输出曲线上的点curve_points = nurbs_curve.generate_curve_points()print("NURBS曲线上的点:")for point in curve_points:print(point)
3. 代码详解
-
Point2D 类:表示二维平面上的一个点,包含点的 x x x 和 y y y 坐标。
-
NURBSCurve 类:该类用于计算NURBS曲线,主要包括以下方法:
__init__():初始化NURBS曲线,包括控制点、权重、阶数和节点向量。如果未提供节点向量,将自动生成一个均匀节点向量。_generate_uniform_knot_vector():生成均匀节点向量。_basis_function():递归计算B样条基函数。calculate_point():计算曲线在参数 t t t 处的点,权重会影响控制点对曲线的贡献。generate_curve_points():生成NURBS曲线上的多个点,用于近似表示曲线的形状。
使用示例
假设我们有4个控制点 ( 0 , 0 ) , ( 1 , 2 ) , ( 3 , 3 ) , ( 4 , 0 ) (0, 0), (1, 2), (3, 3), (4, 0) (0,0),(1,2),(3,3),(4,0),并为其中两个控制点设置较小的权重 0.5 0.5 0.5,这将影响曲线的形状。生成的曲线在权重较大的控制点附近会更接近这些点。
NURBS曲面的扩展
NURBS曲线可以扩展为NURBS曲面。NURBS曲面是由二维控制点网格、权重矩阵以及两个方向的节点向量控制的。
NURBS曲面类实现
# 定义NURBS曲面类
class NURBSSurface:def __init__(self, control_points_grid, weights_grid, degree_u, degree_v, knot_vector_u=None, knot_vector_v=None):"""初始化NURBS曲面:param control_points_grid: 控制点的二维网格,每个点是Point2D 对象:param weights_grid: 权重的二维网格:param degree_u: u方向的NURBS阶数:param degree_v: v方向的NURBS阶数:param knot_vector_u: u方向的节点向量:param knot_vector_v: v方向的节点向量"""self.control_points_grid = control_points_gridself.weights_grid = weights_gridself.degree_u = degree_uself.degree_v = degree_vself.num_control_points_u = len(control_points_grid)self.num_control_points_v = len(control_points_grid[0])# 生成均匀节点向量if knot_vector_u is None:self.knot_vector_u = self._generate_uniform_knot_vector(self.num_control_points_u, self.degree_u)else:self.knot_vector_u = knot_vector_uif knot_vector_v is None:self.knot_vector_v = self._generate_uniform_knot_vector(self.num_control_points_v, self.degree_v)else:self.knot_vector_v = knot_vector_vdef _generate_uniform_knot_vector(self, num_control_points, degree):"""生成均匀的节点向量:param num_control_points: 控制点数量:param degree: NURBS阶数:return: 均匀节点向量"""return [0] * (degree + 1) + list(range(1, num_control_points - degree)) + [num_control_points - degree] * (degree + 1)def calculate_point(self, u, v):"""计算NURBS曲面在参数 (u, v) 处的点:param u: u方向参数值:param v: v方向参数值:return: 返回曲面在 (u, v) 处的 Point2D 点"""numerator_x = 0.0numerator_y = 0.0denominator = 0.0for i in range(self.num_control_points_u):for j in range(self.num_control_points_v):b_u = NURBSCurve._basis_function(self, i, self.degree_u, u)b_v = NURBSCurve._basis_function(self, j, self.degree_v, v)numerator_x += b_u * b_v * self.weights_grid[i][j] * self.control_points_grid[i][j].xnumerator_y += b_u * b_v * self.weights_grid[i][j] * self.control_points_grid[i][j].ydenominator += b_u * b_v * self.weights_grid[i][j]return Point2D(numerator_x / denominator, numerator_y / denominator)def generate_surface_points(self, num_points_u=10, num_points_v=10):"""生成NURBS曲面上的点:param num_points_u: u方向点的数量:param num_points_v: v方向点的数量:return: 返回二维点列表,表示NURBS曲面"""surface_points = []for u in np.linspace(self.knot_vector_u[self.degree_u], self.knot_vector_u[-self.degree_u-1], num_points_u):row = []for v in np.linspace(self.knot_vector_v[self.degree_v], self.knot_vector_v[-self.degree_v-1], num_points_v):row.append(self.calculate_point(u, v))surface_points.append(row)return surface_points
总结
NURBS通过引入权重使得在精确描述几何图形(如圆和椭圆)时更加灵活。本文通过面向对象的思想,详细介绍了NURBS曲线和曲面的实现原理,并给出了Python的具体实现。
相关文章:

使用Python实现图形学曲线和曲面的NURBS算法
目录 使用Python实现图形学曲线和曲面的NURBS算法引言NURBS曲线的数学原理1. NURBS曲线定义2. 权重的作用 NURBS曲线的Python实现1. 类结构设计2. 代码实现3. 代码详解使用示例 NURBS曲面的扩展NURBS曲面类实现 总结 使用Python实现图形学曲线和曲面的NURBS算法 引言 NURBS&a…...

SpringBoot3
文章目录 一、为什么要学习SpringBoot二、SpringBoot介绍2.1 约定优于配置2.2 SpringBoot中的约定三、SpringBoot快速入门3.1 快速构建SpringBoot3.1.1 选择构建项目的类型3.1.2 项目的描述3.1.3 指定SpringBoot版本和需要的依赖3.1.4 导入依赖3.1.5 编写了Controller3.1.6 测试…...

【Text2SQL】领域优质论文分享
解读论文:Enhancing Few-shot Text-to-SQL Capabilities of Large Language Models: A Study on Prompt Design Strategies 1. 重要贡献 这篇论文的主要贡献在于提出了一种新的方法来增强大型语言模型(LLMs)在少量样本(Few-shot…...

2024全国研究生数学建模竞赛(数学建模研赛)ABCDEF题深度建模+全解全析+完整文章
全国研究生数学建模竞赛(数学建模研赛)于9月21日8时正式开赛,赛程4天半,咱这边会在开赛后第一时间给出对今年的6道赛题的评价、分析和解答。包括ABCDEF题深度建模全解全析完整文章,详情可以点击底部的卡片来获取哦。 …...

Java项目中异常处理的最佳实践
1. 异常分类 首先,理解异常的不同类型是合理处理异常的基础。Java中的异常大致可以分为两大类: 受检异常(Checked Exceptions):这些异常必须被捕获或声明抛出,例如IOException。非受检异常(Un…...

CSS基本概念以及CSS的多种引入方式
CSS基本概念 CSS是层叠样式表,又叫级联样式表,简称样式表。CSS的文件后缀为.css,CSS用于HTML文档中元素样式的定义。 CSS的基本语法 CSS的规则由2个主要的部分构成:选择器以及一条或者多条声明。 选测器通常是你血药改变样式的…...

TiDB 简单集群部署拓扑文件
TiDB集群部署 服务器环境部署拓扑 都2024了还在为分库分表烦恼吗😘,用分布式数据库TiDB、OceanBase、华为 GaussDB,你就使劲往里存数据。 早下班、少脱发、脱单! 🙏🏻🙏🏻Ƕ…...

十三 系统架构设计(考点篇)
1 软件架构的概念 一个程序和计算系统软件体系结构是指系统的一个或者多个结构。结构中包括软件的构件,构件 的外部可见属性以及它们之间的相互关系。 体系结构并非可运行软件。确切地说,它是一种表达,使软件工程师能够: (1)分…...

Java-数据结构-二叉树-习题(三)  ̄へ ̄
文本目录: ❄️一、习题一(前序遍历非递归): ▶ 思路: ▶ 代码: ❄️二、习题二(中序遍历非递归): ▶ 思路: ▶ 代码: ❄️三、习题三(后序遍历非递归): ▶ 思路: …...

SpringBoot+Aop+注解方式 实现多数据源动态切换
整体思路: 引入基本依赖SpringBootAopMySqlMyBatislombok在配置文件中配置多个数据源创建数据源配置类用于读取配置编写用于标识切换数据源的注解创建数据源切换工具类DataSourceContextHolder编写切面类用于在注解生效处切换数据源编写配置类,加载数据…...

企业如何高效应对多类型知识产权事务的复杂挑战?
随着企业的发展和创新活动的不断推进,越来越多的企业拥有了大量的专利、商标和软著等知识产权,这些不仅关乎企业的技术创新成果,更直接影响到企业的品牌价值和市场竞争力。然而,当企业拥有多件知识产权时,复杂的申请、…...
openeuler22.03 LTS 源码编译安装nginx1.22.1
openeuler22.03 LTS 源码编译安装nginx1.22.1 下载安装包 #官网下载nginx1.22.1 wget http://nginx.org/download/nginx-1.22.1.tar.gz安装依赖包 #安装依赖包,NGINX是C语言写的,pcre-devel支持正则表达式,openssl 开启加密 [rootproxy ~]…...

图片压缩工具免费怎么找?归纳了这几个压缩工具
有哪些图片压缩工具免费?在数字化时代,图像已成为我们生活中不可或缺的一部分。无论是网站设计、社交媒体分享还是文件传输,高质量的图片都扮演着重要的角色。但高质量往往意味着大文件体积,这可能会导致加载速度变慢或存储空间不…...
【Kubernetes知识点】解读HPA的 thrashing(抖动)问题
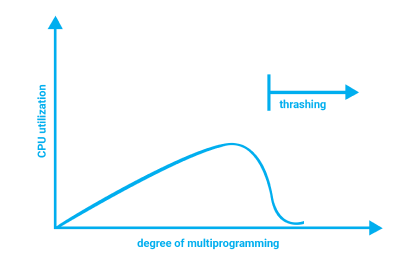
【Kubernetes知识点】解读HPA的 thrashing(抖动)问题 目录 1 概念 1.1 什么是 Thrashing 现象?1.2 HPA 中 Thrashing 产生的原因1.3 解决 Thrashing 的优化措施 1.3.1 设置合适的阈值1.3.2 使用自定义指标和基于负载的自动扩缩1.3.3 增加扩…...

Unity 设计模式 之 结构型模式 -【装饰者模式】【外观模式】【享元模式】【代理模式】
Unity 设计模式 之 结构型模式 -【装饰者模式】【外观模式】【享元模式】【代理模式】 目录 Unity 设计模式 之 结构型模式 -【装饰者模式】【外观模式】【享元模式】【代理模式】 一、简单介绍 二、装饰者模式(Decorator Pattern) 1、什么时候使用装…...

Linux上Qt安装相关的内容及在QtCreator使用QChart模块需要的配置
引言 下面是Ubuntu上Qt安装相关的内容及在QtCreator使用QChart模块需要的配置。 关于Qt安装及环境 Qt的模块 查看已经安装的模块 sudo apt search qt5-安装新的模块 sudo apt install qt5-svg # 安装Qt SVG模块3.查看qt已经安装了哪些模块 dpkg -l | grep libqt安装qt,…...

lettuce引起的Redis command timeout异常
项目使用Lettuce,在自己的环境下跑是没有问题的。在给客户做售前压测时,因为客户端环境比较恶劣,service服务和中间件服务不在同一机房。服务启动后不一会就会出现Redis command timeout异常。 经过差不多两周的追查,最后没办法把…...

【Hadoop】一、Hadoop入门:基础配置、集群配置、常用脚本
基础设置 网络设置 创建好一个 centos 虚拟机,修改网络配置文件: /etc/sysconfig/network-scripts/ifcfg-ens33修改 BOOTPROTO 为 static 以及添加 IPADDR、GATEWAY、DNS1 TYPE"Ethernet" PROXY_METHOD"none" BROWSER_ONLY&quo…...
Ollama:本地运行大模型【含UI界面】
文章目录 Ollama 简介安装 ollamaWindows 安装Docker 安装其它平台安装支持的模型模型清单模型参数与运行内存快速启动 llama 模型llama 模型介绍运行 llama3.1 模型通过 HTTP API 访问ollama 命令语法常用示例特别示例自定义模型创建 Modelfile创建模型并运行集成 Web 页面Ope…...

【论文阅读】Grounding Language with Visual Affordances over Unstructured Data
Abstract 最近的研究表明,大型语言模型(llms)可以应用于将自然语言应用于各种各样的机器人技能。然而,在实践中,学习多任务、语言条件机器人技能通常需要大规模的数据收集和频繁的人为干预来重置环境或帮助纠正当前的…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
