46-堆
目录
1.概念
2.表示
3.三大操作
4.代码实现最大堆(基于数组,编号从0开始)
4.1.根据孩子节点k获取当前父节点的索引
4.2.根据父节点k求左孩子节点下标
4.3.根据父节点k求右孩子节点下标
4.4.判空
4.5.toString()方法
4.6.判断数组中元素是否有序
4.7.查看堆顶元素
4.8.交换当前数组中 i 和 parent 的值
4.9.将value存储在堆中
4.10.元素上浮操作
4.11.取出当前堆的最大值,继续调整堆
4.12.元素下沉操作
4.13.heapify堆化操作:将任意给定的整型数组调整为堆
4.14.测试
5.总代码实现
6.总结
1.概念
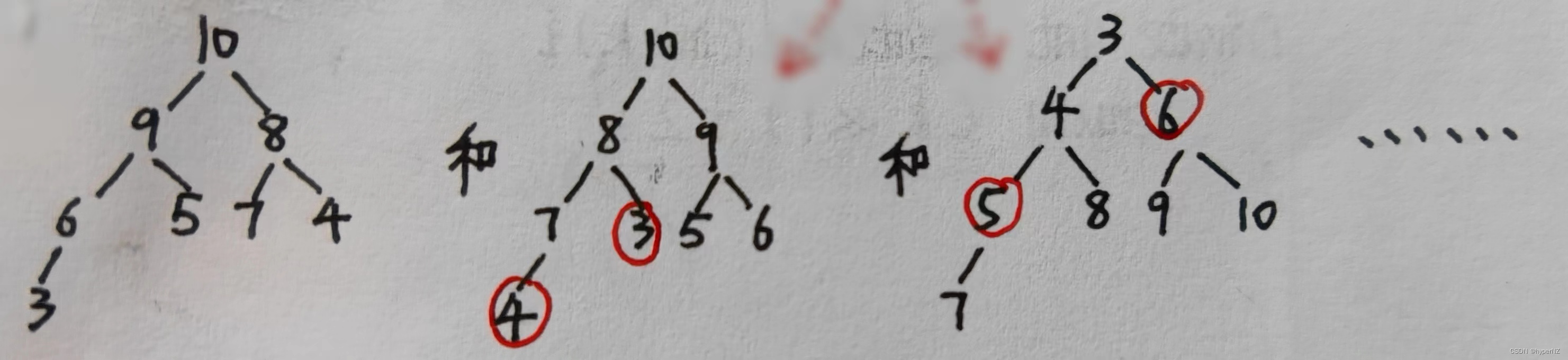
- 逻辑上是一棵完全二叉树,物理上是保存在数组中。
- 基于二叉树的堆叫二叉堆。(堆的实现基本都是二叉树,还有其他的,少)
- 从节点值的要求来看,分为:
- 最大堆(Java中的叫法)/大根堆(C++中的叫法):堆中根节点的值 >= 左右子树节点值。
- 最小堆/小根堆(JDK优先级队列就是小根堆):堆中根节点的值 <= 左右子树节点值。
- 左右子树仍满足此性质。
注:
- 最大/小堆的节点大小关系与节点高度无关!
- 相同的数据下,可能有不同种类的堆,例:可有最大堆构建,也可有最小堆构建。
- 二分搜索树比堆的节点值大小关系要求更严格。
2.表示
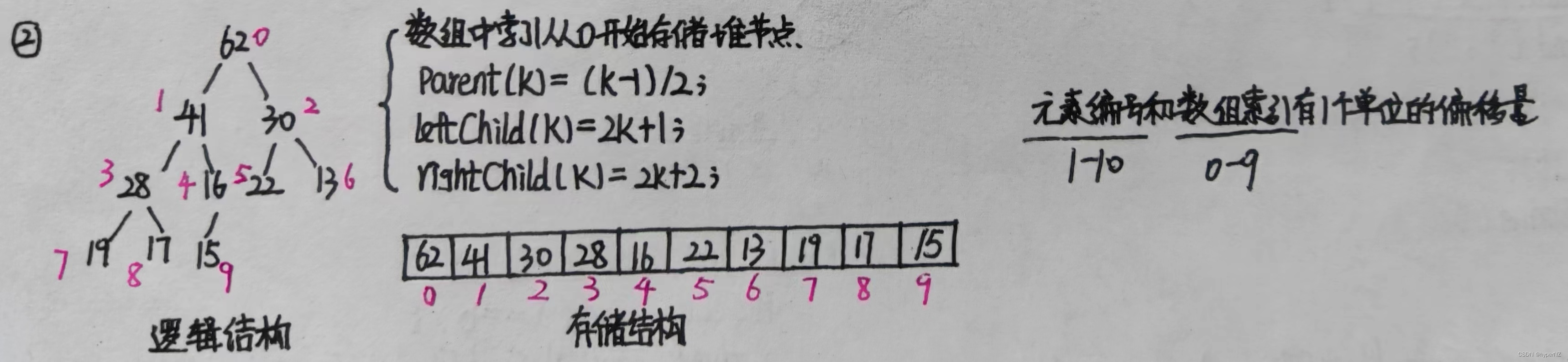
用数组表示(动态数组可扩容),编号表示结构。(2种)
①

②
3.三大操作
- add:向堆末尾添加元素。PS:siftUp元素上浮。
- extractMax:取出当前堆的最大值元素。PS:siftDown元素下沉。
- heapify:堆化(将任意给定的整型数组调整为堆)。PS:siftDown元素下沉。
4.代码实现最大堆(基于数组,编号从0开始)
4.1.根据孩子节点k获取当前父节点的索引
/*** 根据孩子节点k获取当前父节点的索引* @param k* @return*/
private int parent(int k) {return (k - 1) >> 1; //位运算符比除法要快 return (k - 1) / 2;
}4.2.根据父节点k求左孩子节点下标
/*** 根据父节点k求左孩子节点下标* @param k* @return*/
private int leftChild(int k) {return ( k << 1 ) + 1; //2k + 1
}4.3.根据父节点k求右孩子节点下标
/*** 根据父节点k求右孩子节点下标* @param k* @return*/
private int rightChild(int k) {return (k << 1) + 2; //2k + 2
}4.4.判空
/*** 判空* @return*/
public boolean isEmpty() {return data.size() == 0;
}4.5.toString()方法
@Override
public String toString() {StringBuilder sb = new StringBuilder();sb.append("[");for (int i = 0; i < data.size(); i++) {sb.append(data.get(i));if(i != data.size() - 1){sb.append(",");}}sb.append("]");return sb.toString();
}@Override
public String toString() {return data.toString();
}4.6.判断数组中元素是否有序
/*** 判断数组中元素是否有序* @param arr* @return*/
public static boolean isSorted(int[] arr) {for (int i = 0; i < arr.length - 1; i++) { //i < arr.length - 1走不到最后一个元素,arr.length - 1是最后一个元素if(arr[i] < arr[i + 1]) {return false;}}return true;
}4.7.查看堆顶元素
/*** 查看堆顶元素* @return*/
public int peekHeap() {if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}return data.get(0);
}4.8.交换当前数组中 i 和 parent 的值
/*** 交换当前数组中 i 和 parent 的值* @param i* @param parent*/
private void swap(int i, int parent) {int tmp = data.get(i);int parentVal = data.get(parent);data.set(i,parentVal);data.set(parent,tmp);
}4.9.将value存储在堆中
/*** 将value存储在堆中* @param value*/
public void add(int value) {//1.向数组末尾添加元素this.data.add(value);//2.调整当前堆的结构,使其仍然满足最大堆的性质siftUp(data.size() - 1);
}4.10.元素上浮操作
/*** 元素上浮操作* @param i 要上浮的元素索引*/
private void siftUp(int i) {while(i > 0 && data.get(i) > data.get(parent(i))) {swap(i,parent(i));//继续向上判断交换后父节点向上的节点关系i = parent(i);}
}4.11.取出当前堆的最大值,继续调整堆
/*** 取出当前堆的最大值,继续调整堆* @return*/
public int extractMax() {//判断当前堆是否为空if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}int max = data.get(0);//将最后一个元素顶到堆顶int lastElement = data.get(data.size() - 1);data.set(0, lastElement);//删除最后一个元素data.remove(data.size() - 1);//元素下沉siftDown(0);return max;
}4.12.元素下沉操作
/*** 元素下沉操作* @param i 要下沉的元素索引*/
private void siftDown(int i) {//终止条件:当i还有子树时,说明还没判断结束;若左孩子都不存在,则一定不存在右孩子while(leftChild(i) < data.size()) {//此时i索引对应的元素仍然存在左子树,没到叶子节点int j = leftChild(i);//此时还存在右子树if(j + 1 < data.size() && data.get(j + 1 ) > data.get(j)) {//此时右子树的值大于左子树j = j + 1;}//j一定保存了左右子树的最大值索引if(data.get(i) >= data.get(j)) { //此处为何是 >=//如果此处终止条件是 父节点 > 子节点,也可以,不会死循环//以后在写测试用例时,必须要复杂//此时i对应的元素已经下沉到合适位置break;}else{swap(i,j);i = j;}}
}4.13.heapify堆化操作:将任意给定的整型数组调整为堆
/*** heapify堆化操作:将任意给定的整型数组调整为堆* ①自底向上逐渐调整堆的过程,只看非叶子节点,从最后一个非叶子节点(最后一个非叶子节点就是最后一个节点他爸)开始,一次性砍掉所有叶子节点,进行元素的siftDown操作,直到向上走到根节点即可,时间复杂度为O(n)* ②遍历原数组,依次add操作,时间复杂度为O(nlogn)* @param arr*/
public MaxHeap(int[] arr) {//初始化data = new ArrayList<>(arr.length);//1.先将arr的所有元素拷贝到data中for(int i : arr) {data.add(i);}//2.从最后一个非叶子节点开始进行元素下沉for (int i = parent(data.size() - 1); i >= 0 ; i--) {siftDown(i);}
}4.14.测试
public static void main(String[] args) {
// MaxHeap heap = new MaxHeap();
// heap.add(5);
// heap.add(2);
// heap.add(7);
// heap.add(1);
// heap.add(3);
// System.out.println(heap);
//
// int[] ret = new int[5];
// for (int i = 0; i < ret.length; i++) {
// ret[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(ret));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data.length);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// heap.add(data[i]);
// }
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));int n = 10000;int[] data = new int[n];//生成随机数Random random = new Random();for (int i = 0; i < n; i++) {//范围是 0 - Integer.MAX_VALUEdata[i] = random.nextInt(Integer.MAX_VALUE);}MaxHeap heap = new MaxHeap(data);for (int i = 0; i < n; i++) {data[i] = heap.extractMax();}System.out.println(isSorted(data));
}5.总代码实现
import java.util.*;/*** 基于数组实现的最大堆* 编号从0开始,假设当前节点为i,i>0* parent = (i - 1) / 2;* 若有左右孩子,保证 2i + 1 或 2i + 2 < data.length;* left = 2i + 1;* right = 2i + 2;*/
public class MaxHeap {//具体存储元素的动态数组private List<Integer> data;//无参构造public MaxHeap() {this(10);}//指定容量大小public MaxHeap(int initCap) {this.data = new ArrayList<>(initCap);}/*** 根据孩子节点k获取当前父节点的索引* @param k* @return*/private int parent(int k) {return (k - 1) >> 1; //位运算符比除法要快 return (k - 1) / 2;}/*** 根据父节点k求左孩子节点下标* @param k* @return*/private int leftChild(int k) {return ( k << 1 ) + 1; //2k + 1}/*** 根据父节点k求右孩子节点下标* @param k* @return*/private int rightChild(int k) {return (k << 1) + 2; //2k + 2}/*** 判空* @return*/public boolean isEmpty() {return data.size() == 0;}@Overridepublic String toString() {return data.toString();}/*** 判断数组中元素是否有序* @param arr* @return*/public static boolean isSorted(int[] arr) {for (int i = 0; i < arr.length - 1; i++) { //i < arr.length - 1走不到最后一个元素,arr.length - 1是最后一个元素if(arr[i] < arr[i + 1]) {return false;}}return true;}/*** 查看堆顶元素* @return*/public int peekHeap() {if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}return data.get(0);}/*** 交换当前数组中 i 和 parent 的值* @param i* @param parent*/private void swap(int i, int parent) {int tmp = data.get(i);int parentVal = data.get(parent);data.set(i,parentVal);data.set(parent,tmp);}/*** 将value存储在堆中* @param value*/public void add(int value) {//1.向数组末尾添加元素this.data.add(value);//2.调整当前堆的结构,使其仍然满足最大堆的性质siftUp(data.size() - 1);}/*** 元素上浮操作* @param i 要上浮的元素索引*/private void siftUp(int i) {while(i > 0 && data.get(i) > data.get(parent(i))) {swap(i,parent(i));//继续向上判断交换后父节点向上的节点关系i = parent(i);}}/*** 取出当前堆的最大值,继续调整堆* @return*/public int extractMax() {//判断当前堆是否为空if(data.size() == 0) {throw new NoSuchElementException("heap is empty!");}int max = data.get(0);//将最后一个元素顶到堆顶int lastElement = data.get(data.size() - 1);data.set(0, lastElement);//删除最后一个元素data.remove(data.size() - 1);//元素下沉siftDown(0);return max;}/*** 元素下沉操作* @param i 要下沉的元素索引*/private void siftDown(int i) {//终止条件:当i还有子树时,说明还没判断结束;若左孩子都不存在,则一定不存在右孩子while(leftChild(i) < data.size()) {//此时i索引对应的元素仍然存在左子树,没到叶子节点int j = leftChild(i);//此时还存在右子树if(j + 1 < data.size() && data.get(j + 1 ) > data.get(j)) {//此时右子树的值大于左子树j = j + 1;}//j一定保存了左右子树的最大值索引if(data.get(i) >= data.get(j)) { //此处为何是 >=//如果此处终止条件是 父节点 > 子节点,也可以,不会死循环//以后在写测试用例时,必须要复杂//此时i对应的元素已经下沉到合适位置break;}else{swap(i,j);i = j;}}}/*** heapify堆化操作:将任意给定的整型数组调整为堆* ①自底向上逐渐调整堆的过程,只看非叶子节点,从最后一个非叶子节点(最后一个非叶子节点就是最后一个节点他爸)开始,一次性砍掉所有叶子节点,进行元素的siftDown操作,直到向上走到根节点即可,时间复杂度为O(n)* ②遍历原数组,依次add操作,时间复杂度为O(nlogn)* @param arr*/public MaxHeap(int[] arr) {//初始化data = new ArrayList<>(arr.length);//1.先将arr的所有元素拷贝到data中for(int i : arr) {data.add(i);}//2.从最后一个非叶子节点开始进行元素下沉for (int i = parent(data.size() - 1); i >= 0 ; i--) {siftDown(i);}}public static void main(String[] args) {
// MaxHeap heap = new MaxHeap();
// heap.add(5);
// heap.add(2);
// heap.add(7);
// heap.add(1);
// heap.add(3);
// System.out.println(heap);
//
// int[] ret = new int[5];
// for (int i = 0; i < ret.length; i++) {
// ret[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(ret));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data.length);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// heap.add(data[i]);
// }
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));// int[] data = {17,90,68,12,15,14,70,30,20};
// MaxHeap heap = new MaxHeap(data);
// //依次调用extractMax()->集合恰好是一个降序集合
// for (int i = 0; i < data.length; i++) {
// data[i] = heap.extractMax();
// }
// System.out.println(Arrays.toString(data));int n = 10000;int[] data = new int[n];//生成随机数Random random = new Random();for (int i = 0; i < n; i++) {//范围是 0 - Integer.MAX_VALUEdata[i] = random.nextInt(Integer.MAX_VALUE);}MaxHeap heap = new MaxHeap(data);for (int i = 0; i < n; i++) {data[i] = heap.extractMax();}System.out.println(isSorted(data));}
}6.总结
将任意数组调整为堆,而后依次extractMax的操作得到的就是一个排序数组——时间复杂度O(nlogn)。
需要开辟一个和原数组大小完全相同的临时空间——空间复杂度O(n)。
优化:原地堆排序。
相关文章:

46-堆
目录 1.概念 2.表示 3.三大操作 4.代码实现最大堆(基于数组,编号从0开始) 4.1.根据孩子节点k获取当前父节点的索引 4.2.根据父节点k求左孩子节点下标 4.3.根据父节点k求右孩子节点下标 4.4.判空 4.5.toString()方法 4.6.判断数组中…...

Mysql高可用高性能存储应用系列3 - mysqld_multi配置主从集群
概述 主从复制要解决的问题,1)写操作锁表,影响读操作,影响业务。2)数据库备份。3)随着数据增加,I/O操作增多,单机出现瓶颈。 主从复制就是从服务器的主节点,复制到多个从节点,默认采用异步的方…...
)
天干地支(Java)
题目描述 古代中国使用天干地支来记录当前的年份。 天干一共有十个,分别为:甲(jiǎ)、乙(yǐ)、丙(bǐng)、丁(dīng)、戊(w)、己&a…...
码住,虹科工业树莓派应用小tips
在应用虹科工业树莓派进行项目开发的过程中,我们会应用到各种功能,部分功能看似不起眼,但是在实际应用开发过程中却非常重要。接下来虹科分享几个工业树莓派在应用过程中经常会遇到的几个问题,并分享解决方案,帮助大家…...
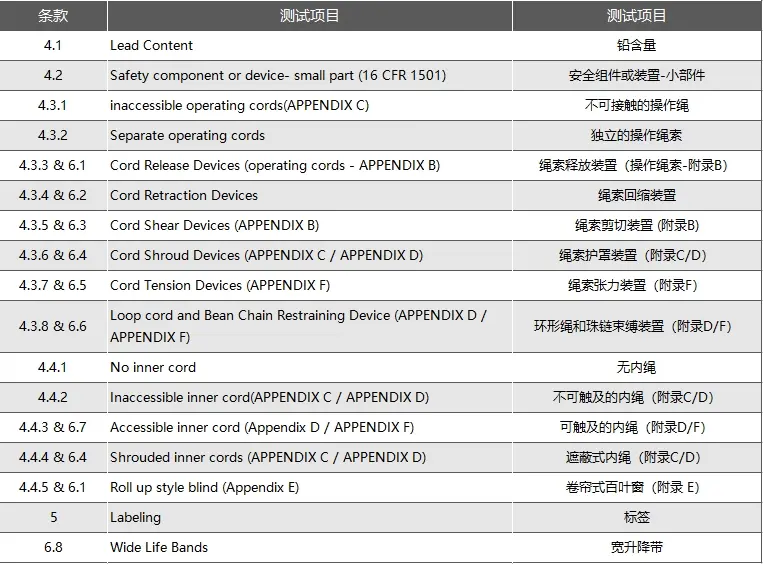
美国新规-带绳窗帘亚马逊ANSI/WCMA A100.1-20测试标准详解
亚马逊要求所有有线窗帘都经过测试,符合下列特定法规或标准要求: 商品法规/标准要求带绳窗帘以下所有项: 显示检测结果符合 ANSI/WCMA A100.1-2018(带绳窗帘商品的美国国家安全标准)的检测报告。 美国消费品安全委员…...
)
【华为OD机试 2023最新 】 模拟商场优惠打折(C++)
题目描述 模拟商场优惠打折,有三种优惠券可以用,满减券、打折券和无门槛券。 满减券:满100减10,满200减20,满300减30,满400减40,以此类推不限制使用; 打折券:固定折扣92折,且打折之后向下取整,每次购物只能用1次; 无门槛券:一张券减5元,没有使用限制。 每个…...
前端直接生成GIF动态图实践
前言去年在博客中发了两篇关于GIF动态生成的博客,GIF图像动态生成-JAVA后台生成和基于FFmpeg的Java视频Mp4转GIF初探,在这两篇博客中都是采用JAVA语言在后台进行转换。使用JAVA的同学经过自己的改造和开发也可以应用在项目上。前段时间有朋友私下问&…...

2023年Java岗面试八股文及答案整理(金三银四最新版)
春招,秋招,社招,我们Java程序员的面试之路,是挺难的,过了HR,还得被技术面,小刀在去各个厂面试的时候,经常是通宵睡不着觉,头发都脱了一大把,还好最终侥幸能够…...

centos8上安装redis
一、安装前准备 在安装Redis之前,需要确保CentOS 8系统已经安装了EPEL存储库和Redis的依赖库。 安装EPEL存储库 EPEL存储库是一个由Fedora项目提供的额外软件包仓库,包含了许多常用的软件包。在CentOS 8系统上,可以通过以下命令安装EPEL存储…...
新六级阅读通关特训
词汇题(55道) 1. You should carefully think over_____ the manager said at the meeting. A. that B. which C. what D. whose 1.选C,考察宾语从句连接词,主句谓语动词think over后面缺宾语,后面的宾语从句谓语动…...
【AI绘画】如何使用Google Colab安装Stable Diffusion
【AI绘画】如何在Colab安装的Stable Diffusion背景准备安装查看资源仓库跳转到Colab运行Stable Diffusion基础设置启动运行访问Stable Diffusion WebUI界面模型资源推荐背景 本地部署Stable Diffusion过程麻烦,对机器配置要求高,GPU 4G,然而…...
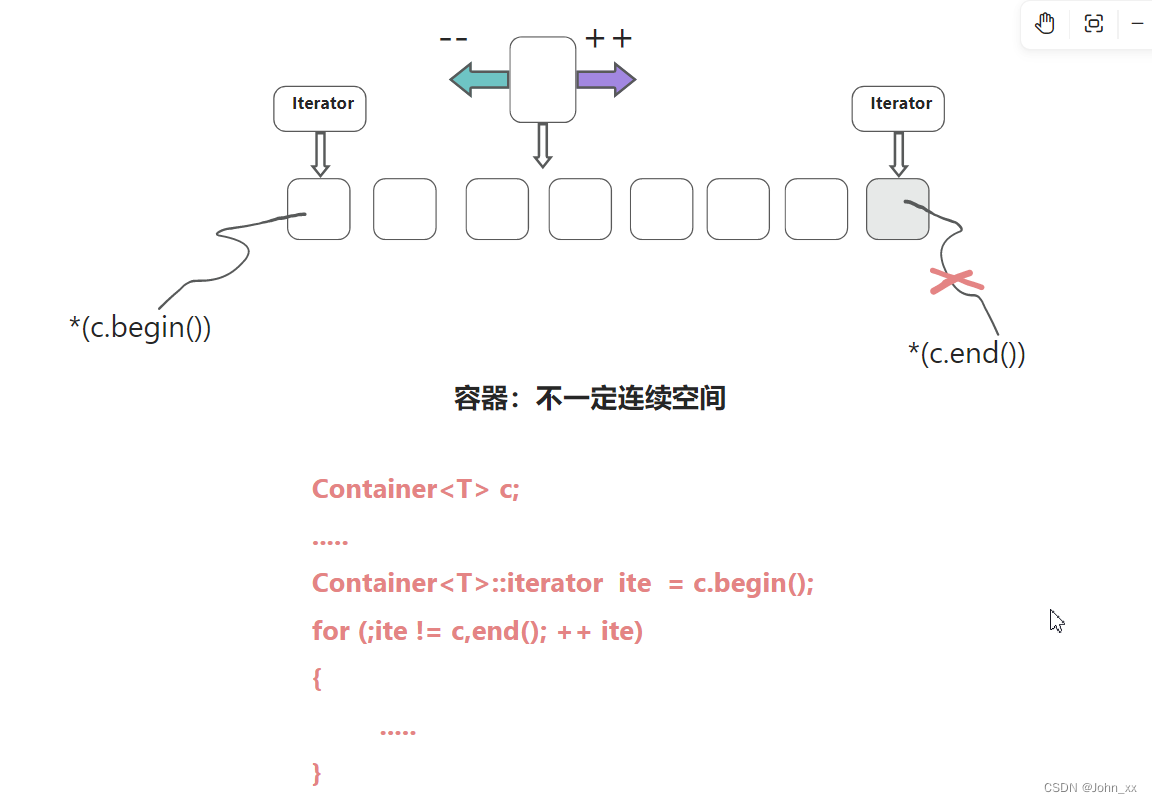
C++:STL架构图
STL架构图1:仿函数2:算法架构图算法库 再看一下这个实例 #include<vector> #include<algorithm> #include<functional> #include<iostream> using namespace std;int main() {int i[6] {1,2,3,4,5,6};vector<int,allocato…...
[Ubuntu][网络][教程]端口转发以及端口管理
1. 平台介绍 Ubuntu 20.04 LTS Armv7 2. 端口管理 进行端口转发之前,要先对端口进行一系列设置 2.1 安装ufw sudo apt install ufw2.2 开启22端口 开启ufw之后,默认的22端口不会自动打开,使用SSH的话需要手动打开 sudo ufw allow 22…...

@Scheduled 定时任务不执行
一、排查代码中添加的定时任务步骤是否正确 启动类上加 EnableScheduling 注解定时任务类上加Component定时方法上加Scheduled Scheduled(cron "0 19 16 * * ?")public void cron() {log.info("定时任务开启:---");}二、排查是否任务阻塞&am…...
)
我是怎样被卷的(二)
被卷的过程,虽然是辛苦种种(加班熬夜陪着爆肝),但终有所值。没有这样的高压环境,我都不知道自己居然可以这么的优秀。 我要答复的问题,分为4类。一是我自己已经掌握的,二是需要找别人获取的&am…...
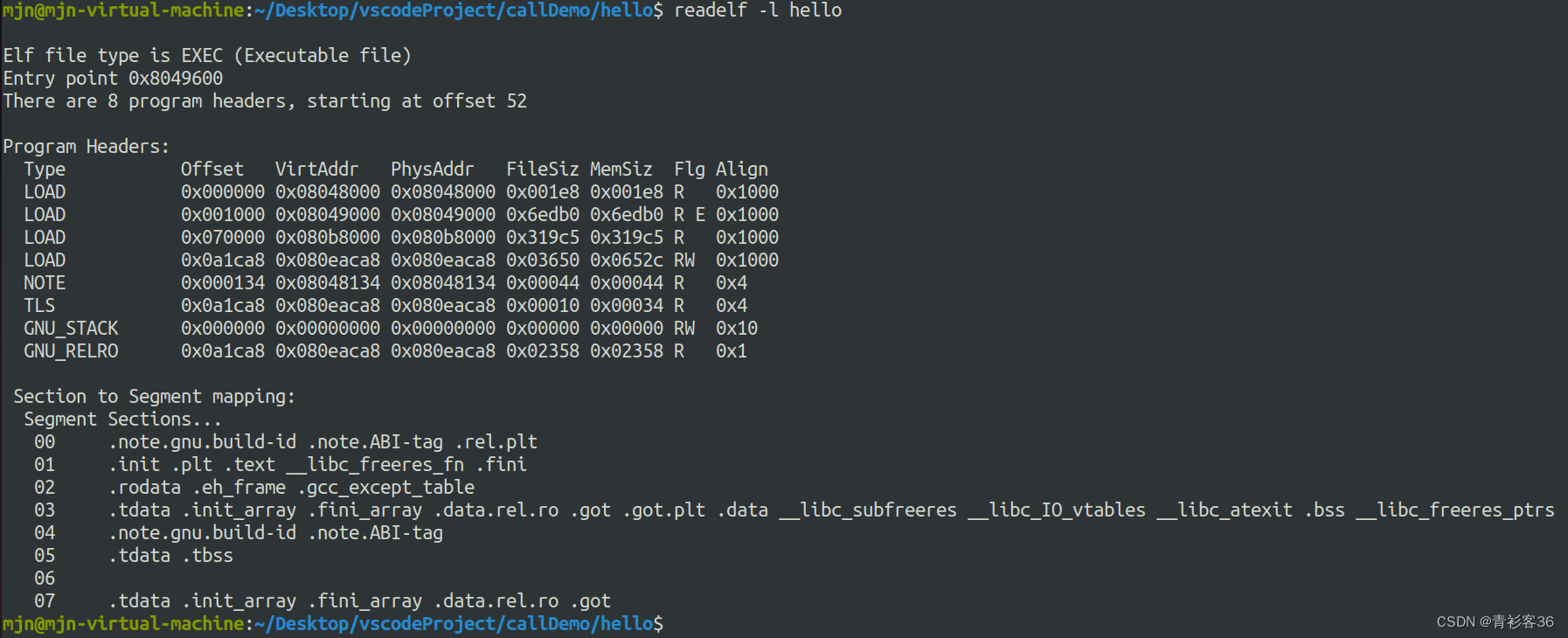
Linux- 浅谈ELF目标文件格式
理解了进程的描述和创建之后,自然会想到我们编写的可执行程序是如何作为一个进程工作的?这就涉及可执行文件的格式、编译、链接和装载等相关知识。 这里先提一个常见的名词“目标文件”,是指编译器生成的文件。“目标”指目标平台,…...

C++ MVC模式
概述 C是一种流行的编程语言,它可以用于构建各种类型的应用程序,包括Web应用程序、桌面应用程序和移动应用程序。在这里,我将为您介绍C中的MVC模式,以及如何在C中实现MVC模式。 MVC(Model-View-Controller࿰…...

IntelliJ IDEA2021安装教程
1.鼠标右击【JetBrains 2021】压缩包(win11系统需先点击“显示更多选项”)选择【解压到“JetBrains 2021”】 2.打开解压后的文件夹,鼠标右击您需要安装的软件名称(如:IdealU-2021.3.1)选择【以管理员身份运…...

day16—选择题
文章目录1.计算每位学生的多学科加总成绩的SQL是(C)2.以下哪个不是与Mysql服务器相互作用的通讯协议(B)3.设有两个事务T1,T2,其并发操作如下所示,下面评价正确的是(D)4.如果事务T获得了数据项Q上的排它锁&a…...
 基本语法)
LLVM 的中间代码(IR) 基本语法
LLVM 的中间代码(IR) 基本语法 以下是 LLVM IR 的基本语法和每个语法的实例代码: 1.数据类型 LLVM IR 支持多种数据类型,包括整型、浮点型、指针型和向量型等。以下是 LLVM IR 中定义不同类型的语法和示例代码: 整…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...
