数据结构不再难懂：带你轻松搞定排序算法

数据结构入门学习（全是干货）——排序算法（下）

1 快速排序

1.1 算法概述

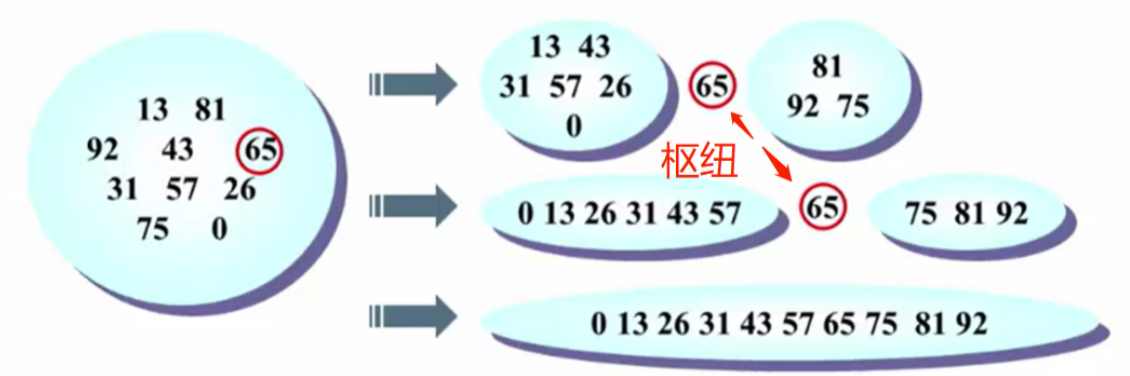
快速排序采用分而治之的策略，与归并排序相似。其核心在于选择一个主元（pivot）作为分割点。

1. 分而治之
   1. 主元(pivot)=>中枢枢纽的意思

伪码描述
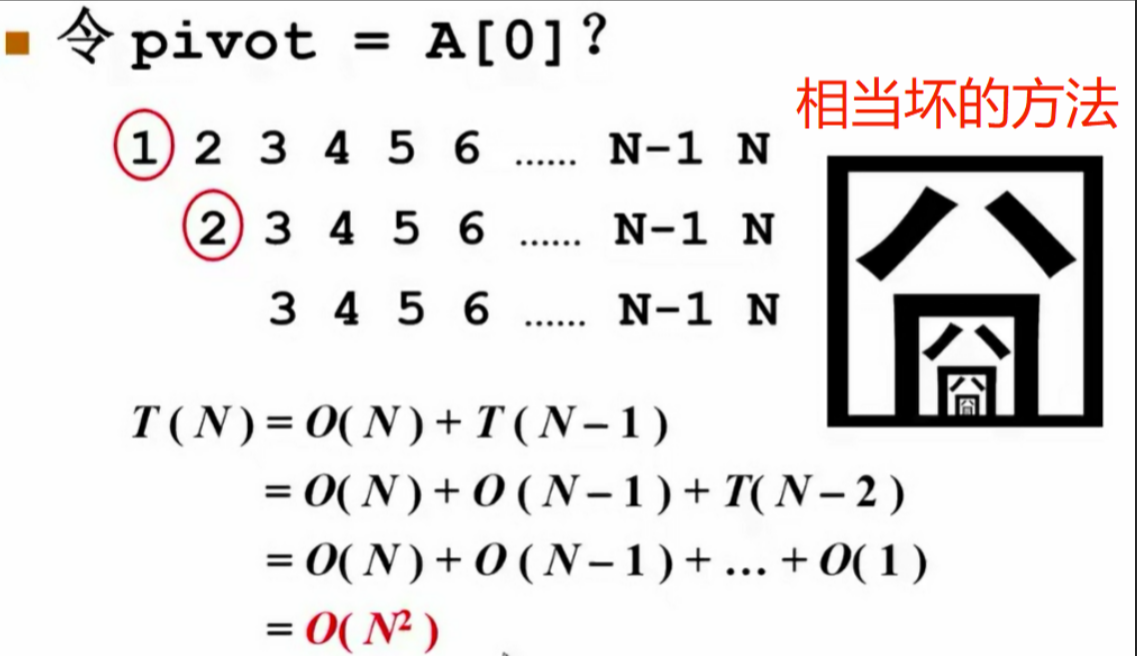
快速排序的最佳情况是每次都能将数组均分。

void Quicksort( ElementType A[],int N )
{if( N < 2 ) return;pivot = 从A[]中选一个主元;//主元的选择决定了快速排序到底快不快将S = { A[] \ pivot }将除了主元以外的元素分成两个独立子集://怎么分A1 = {a属于S | a <= pivot }和A2 = {a属于S | a >= pivot };//一部分由小于等于pivot元素来组成的，另一部分由大于等于pivot元素组成A[] = Quicksort(A1,N1) U {pivot} U Quicksort(A2,N2);
}

什么是快速排序算法的最好情况？每次正好中分

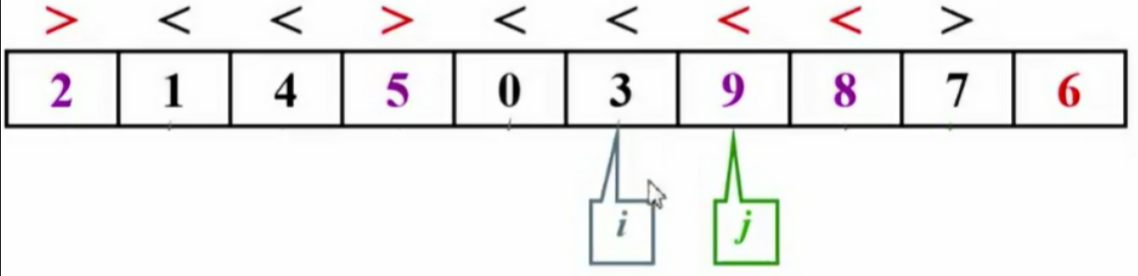
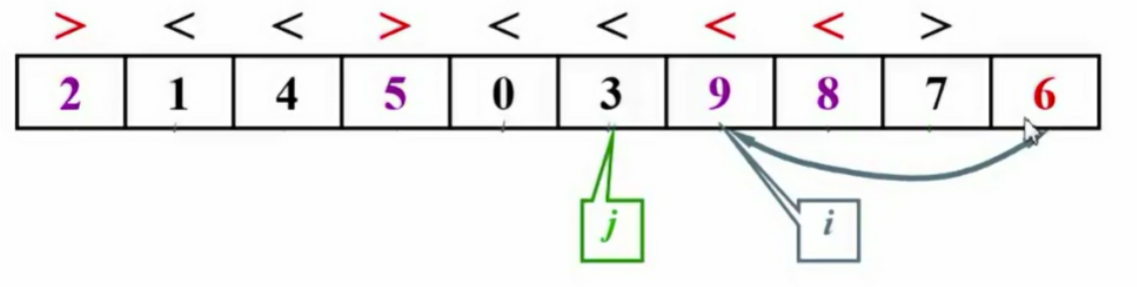
1.2 选主元

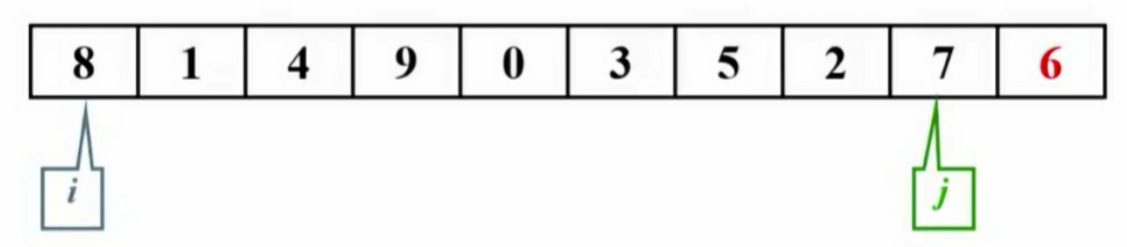
1. 随机选择主元：使用 rand() 函数会影响性能。
2. 取头、中、尾的中位数作为主元：例如，对于8、12、3，选择8为主元。

ElementType Median3( ElementType A[],int Left,int Right )
{int Center = ( Left + Right ) / 2;if( A[ Left ] > A[ Center ] )//三步的比较跟交换(保证从左到右的大小顺序)。左边比中间大Swap( &A[ Left ],&A[ Center ] );if( A[ Left ] > A[ Right ] )//左边比右边大Swap( &A[ Left ],&A[ Right ] );if( A[ Center ] > A[ Right ] )//中间比右边大Swap( &A[ Center ],&A[ Right ] );//这样三步交换下来，左边一定是最小的那个Swap( &A[ Center ],&A[ Right-1 ] );//将pivot藏到右边(为了之后方便，先将Center放到现在需要考虑的子列的最右边)，然后就只需要考虑A[Left + 1]....A[ Right - 2]return A[ Right - 1];//返回pivot
}

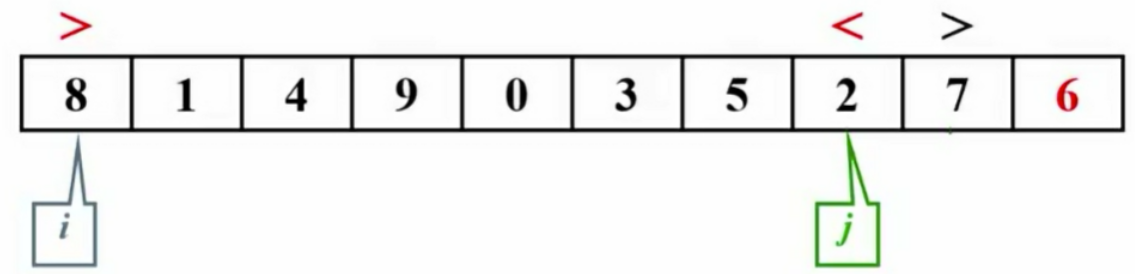
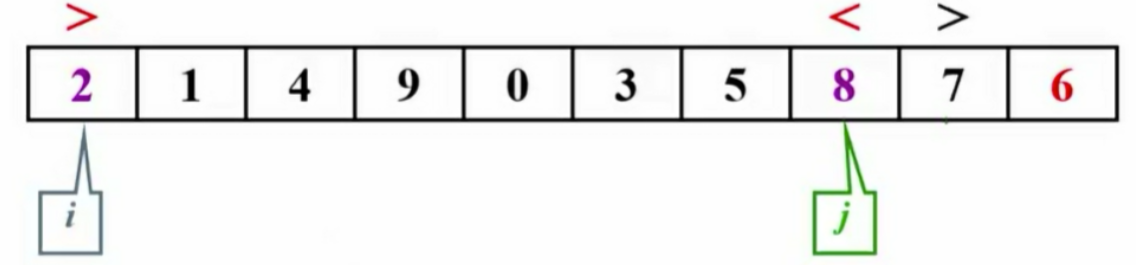
1.3 子集划分

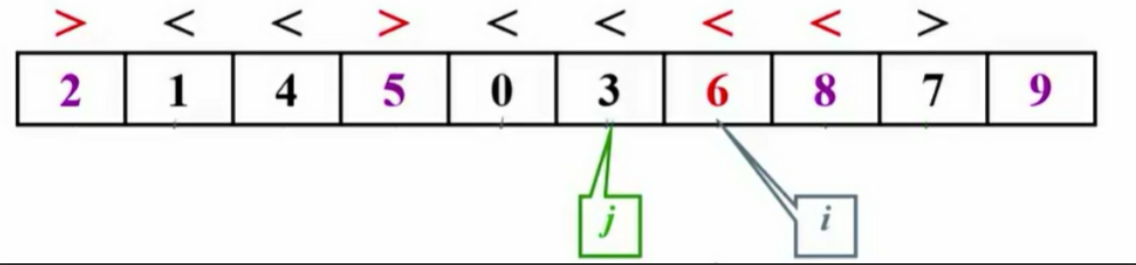
1. i和j并非C语言指针，而是指向存放位置。
2. 主元被移至最右侧。
3. 对比主元与i、j的值并进行交换，直至完成分区。
   1. 
   2. 
   3. 
   4. 
   5. 

快速排序的优势：

• 每次选择的主元最终会被放在其正确位置。
• 相比于插入排序，不必每次都移动其他元素。

注意事项：

1. 如果存在与主元相等的元素：
   • 停止交换会导致不必要的多次交换，复杂度为NlogN。
   • 继续移动指针可能导致主元位置不稳定，复杂度为N²。
   • 结论：选择停止交换更为有效。

小规模数据处理：

• 对于小于100的元素，可能插入排序更快。
• 解决方案：当数据规模小于设定阈值时，停止递归，直接调用插入排序。

1.4 算法实现

void Quicksort( ElementType A[],int Left,int Right )
{if( Cutoff <= Right - Left ){Pivot = Median3( A,Left,Right );//pivot是主元的意思，在这里返回的不仅仅只是一个主元的值//这里的Left参数是最小值，Right参数是最大值。真正的主元被藏在了Right-1的地方i = Left; j = Right - 1;for(;;){while(A[ ++i ] < Pivot ){}while(A[ --j ] < Pivot ){}if( i < j)Swap( &A[i],&A[j] );//i < j则证明中间还有其他元素，这时候就可以调换//如果i > j则这个子集划分应该结束了else break;}Swap( &A[i],&A[Right-1]);//把藏在right-1这个位置的主元换到A[i]的位置上面去Quicksort(A,Left,i-1);//递归的左半部分Quicksort(A,i+1,Right);//递归的右半部分   }elseInsertion_Sort(A+Left,Right-Left+1);//Right-Left+1：待排序列的总个数；A+Left：开始的地方
}

快速排序的标准接口设计

void Quick_Sort(ElementType A[], int N) 
{ /* 这里写什么？如下*/Quicksort( A, 0, N-1 );
}

---

2 表排序

2.1 算法概述

表排序适用于待排元素为复杂结构（如书籍）。其特点是不移动原始数据，仅移动指向它们位置的指针。

间接排序：

• 仅移动指针，通过定义指针数组作为表。
• 定义一个指针数组作为"表"(table)
• 
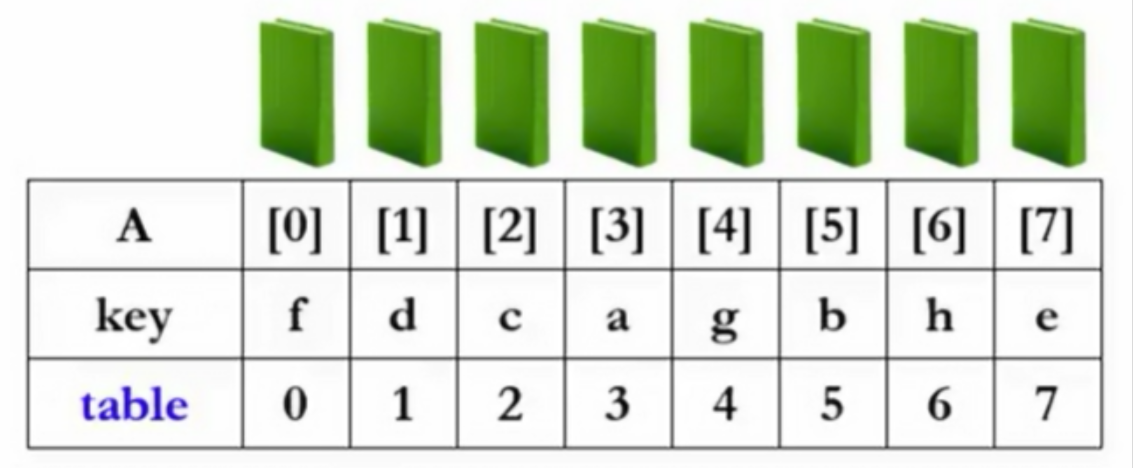
• 交换的只是table的整数(指针)，得到
• 

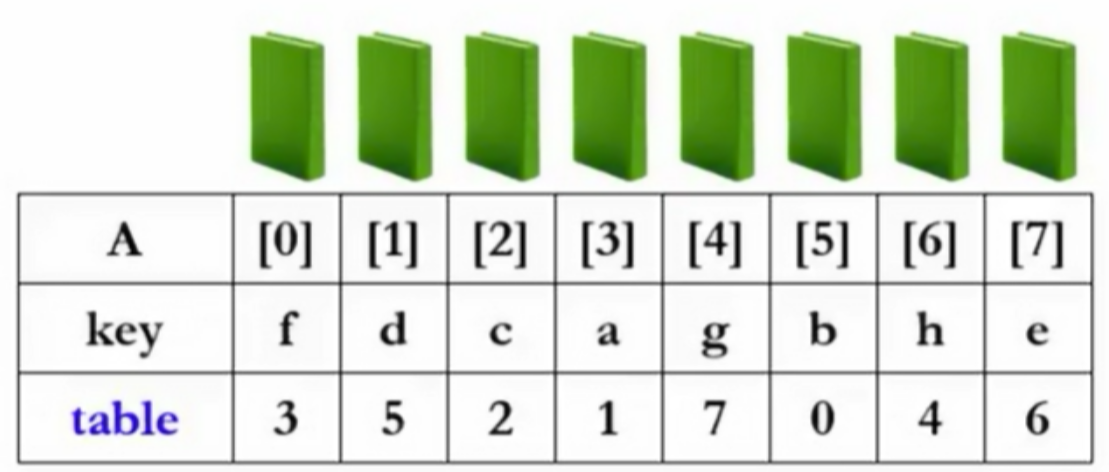
2.2 物理排序

N个元素可由独立环组成。环内元素依赖于其指针值，形成互不交集的独立结构。

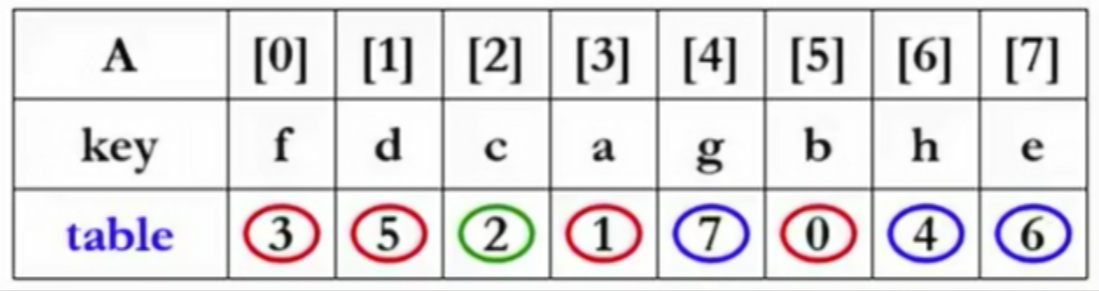
环判断：
每访问空位后，令 table[i] = i。当 table[i] == i 时，环结束。

复杂度分析：

1. 最好情况：初始即有序。
2. 最坏情况：有N/2个环，每个环包含2个元素，移动需3N/2次。
3. 时间复杂度：T = O(mN)，m为每个元素的复制时间。

---

3 基数排序

基于比较的排序算法其最坏时间复杂度下界为O(NlogN)。基数排序是一种非比较排序。

3.1 桶排序

基数排序是桶排序的扩展，通过数组作为指针的桶来存储数据。

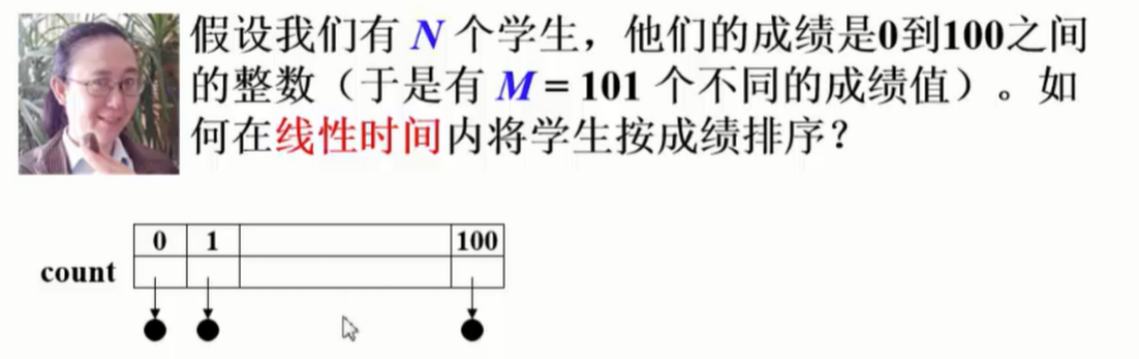
count是数组，这个数组的每一个元素都是一个指针，一开始被初始化为空链表的头指针，所以一开始有101个空链表(对应了101个空的桶 )

假设一个学生考88分：先找到88这个桶，然后把学生信息插到这个链表的表头里

伪码描述
void Bucket_Sort(ElementType A[],int N)
{count[]初始化;while(读入一个学生成绩grade)将该生插入count[grade]链表;for( i=0;i<M;i++){if( count[i] )//桶不为空输出整个count[i]链表;}
}
桶排序算法的时间复杂度T(M, N)是多少？	T(N,M) = O(M+N)当M非常小的时候(例如4w个学生只有101个不同成绩值，那这个时候其实就相当于一种线性的算法)

3.2 基数排序

如果M>>N的话怎么办？

处理值在0到999之间的整数时，每位数有十种可能。

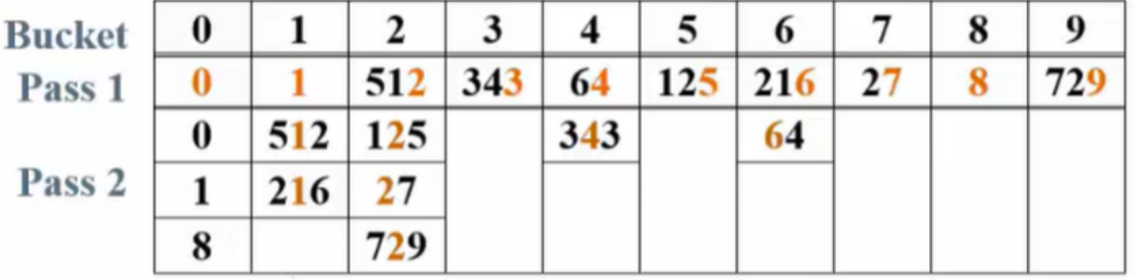
输入序列：64，8，216，512，27，729，0，1，343，125用"次位优先"(Least Significant Digit)=>简称LSD算法//什么是次位优先？假设目前手里是216，这个时候6 个位数是最次位，2 百位数是主位(有一种算法是主位优先)//比较先从个位数开始

步骤：

1. 建立十个桶。

   

2. 根据个位数分配到相应的桶。

   

3. 根据十位数分配。

   

4. 根据百位数分配。

   

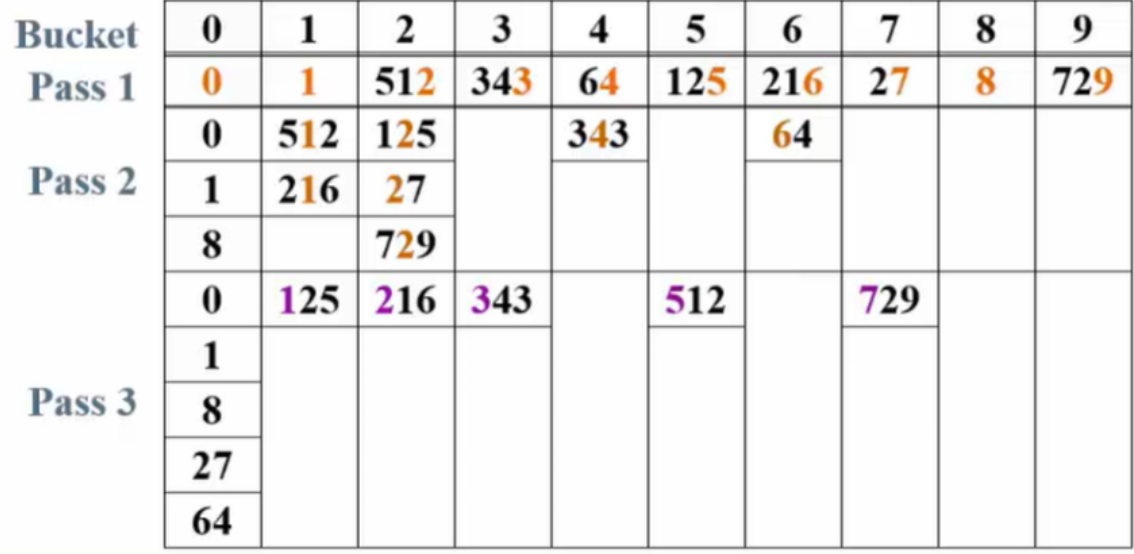
复杂度：
设元素个数为N，基数为B，LSD的趟数为P，最坏时间复杂度为：T=O(P(N+B))。

3.3 多关键字排序

基数排序适用于多关键字排序：

1. 主位优先：为每种花色建立桶，内部排序后合并。
2. 次位优先：为面值建桶，直接合并结果，后续再根据花色建立桶。

次位优先方法效率更高，时间复杂度更低。

---

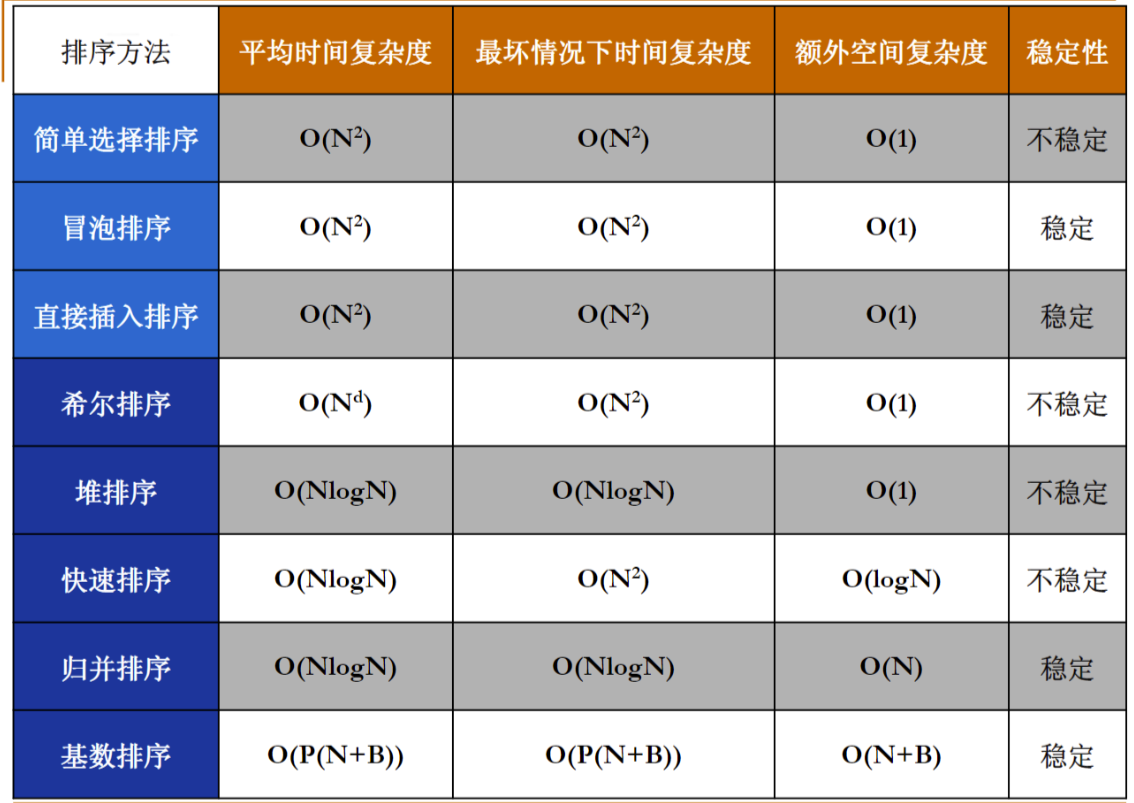
4 排序算法的比较

前三个算法为简单排序，时间复杂度较差，但实现简单且不需额外空间。

• 冒泡排序与插入排序：稳定，但性能较差。
• 简单选择排序：不稳定，性能差。
• 希尔排序：打破下界，复杂度最坏情况下为O(N²)，但仍不稳定。
• 堆排序与归并排序：理论时间复杂度均为O(NlogN)，归并排序稳定，但需额外空间，处理大数据时可能会受到限制。