【算法】反向传播算法

David Rumelhart 是人工智能领域的先驱之一，他与 James McClelland 等人在1986年通过其著作《Parallel Distributed Processing: Explorations in the Microstructure of Cognition》详细介绍了反向传播算法（Backpropagation），这一算法为多层神经网络的训练提供了有效的途径，是深度学习发展的重要里程碑之一。

反向传播算法的核心思想：

反向传播（Backpropagation）算法是基于梯度下降法的一种优化算法，用来训练多层感知器（MLP）等神经网络模型。它的主要思想是，通过逐层计算误差的梯度，并向网络的反方向传播这些误差，更新神经网络的权重，以最小化损失函数。

以下是反向传播算法的基本步骤及其对应的数学公式：

一、前向传播（Forward Propagation）

前向传播的目的是计算神经网络的输出。对于第 l 层的线性组合和激活值：

1. 线性组合：

这里，W(l) 是权重矩阵，a(l−1) 是第 l−1 层的激活值，b(l) 是偏置项。

2. 激活值：

然后通过激活函数 g，得到第 l 层的激活值：

二、 损失函数计算（Loss Function Calculation）

网络的输出和真实标签（目标值）之间的差异通过损失函数来度量。例如，对于回归问题常用均方误差（MSE），对于分类问题常用交叉熵损失（Cross Entropy）。假设损失函数为 L，我们的目标是最小化 L。

三、 反向传播（Backpropagation）

在反向传播阶段，我们通过链式法则计算损失函数对各层权重 W(l) 和偏置 b(l) 的梯度，即：

这些梯度表示每个权重和偏置对最终损失 L 的影响。它们通过链式法则逐层向前回传，详细步骤如下：

1. 损失相对于第 l 层输出的导数：

2. 损失相对于权重的导数：

前向传播中线性组合的公式，可以看到，z(l) 是由 W(l)和 a(l−1) 相乘得到的。因此，z(l) 对 W(l) 的导数为：

通过链式法则计算损失函数对权重 W(l) 的导数：

得到结果：

这里，a^{(l-1)}T 是上一层的激活值的转置，目的是确保矩阵的维度正确。由于 W(l) 是一个矩阵，通常 a(l−1) 是一个列向量，因此 a^{(l-1)}T 是一个行向量。

3. 损失相对于偏置的导数：

在线性组合公式中，偏置 b(l) 是直接加到每个神经元的线性组合 z(l) 中的。因此，z(l) 对 b(l) 的导数是 1：

通过链式法则，我们可以计算损失函数 L 对偏置 b(l) 的导数：

所以：

4. 损失相对于第 l−1层线性组合 z(l−1)的导数：

根据线性组合的公式，z(l) 对 a(l−1) 的导数是权重矩阵 W(l)：

通过链式法则，损失函数对上一层激活值 a(l−1) 的导数可以表示为损失函数对当前层线性组合 z(l) 的导数乘以 z(l) 对 a(l−1) 的导数：

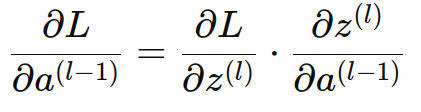
代入前面推导出的公式：

为了保持一致性，我们通常将 W(l) 转置，使得矩阵运算中的维度保持一致：

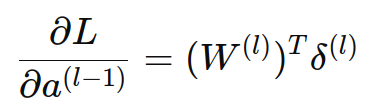
因为每一层的激活值 a(l−1) 是通过激活函数 g(z(l−1)) 得到的：

所以：

即：

⊙ 表示逐元素相乘（Hadamard 乘积），激活函数是逐元素应用到每个神经元输出的，而不是对整个向量进行操作。因此，第 l 层的每个神经元在反向传播时都会依赖于其对应的激活函数导数。

四、 权重和偏置更新（Weight and Bias Update）

使用梯度下降法，根据反向传播计算得到的梯度更新权重和偏置。

1. 权重更新公式：

对于第 l 层的权重 W(l)，更新公式为：

其中：

• η 是学习率。
• ∂W(l)∂E​=δ(l)(a(l−1))T 是损失函数对第 l 层权重的梯度。

2. 偏置更新公式：

类似地，第 l 层的偏置 b(l) 更新公式为：

五、 循环迭代

通过多次迭代（通常称为训练迭代（epochs）），重复进行前向传播、损失函数计算、反向传播以及权重和偏置的更新，直到网络收敛，即损失函数的值不再显著下降，或者达到了预设的迭代次数。

Rumelhart 对反向传播算法的贡献：

David Rumelhart 及其同事的主要贡献在于：

• 他们系统化地提出了反向传播算法，使得该算法可以有效应用于多层神经网络的训练，解决了之前单层感知器模型的局限性。
• 他们展示了如何通过反向传播算法训练深层网络，使得网络能够从数据中学习复杂的模式表示。这为后来的深度学习发展奠定了基础。

反向传播的意义与局限：

反向传播算法是现代深度学习的核心之一，它使得多层神经网络能够成功训练，解决了许多复杂的任务（如图像识别、语音识别等）。但是，它也有一些局限性，例如：

• 梯度消失问题（vanishing gradient）：在深层神经网络中，反向传播的梯度逐渐减小，导致前几层权重更新非常缓慢。
• 训练时间长：当网络层数增加或数据集规模扩大时，训练时间可能会变得非常长。

尽管如此，反向传播算法依然是当今神经网络训练的基础，配合现代改进的优化方法（如Adam、RMSprop等）和技术（如Batch Normalization、Dropout等），反向传播已经极大地提升了神经网络的学习效率和表现。