C++ 二叉树
1. 二叉搜索树
1.1 二叉搜索树概念
二叉搜索树又称二叉排序树,他或者是一棵空树,或者是具有以下性质的二叉树:
①若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
②若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
③它的左右子树也分别为二叉搜索树

1.2 二叉搜索树操作

int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
1.二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到空,还没找到,这个值不存在。
2.二叉搜索树的插入
插入的具体过程如下:
a、树为空,则直接新增节点,赋值给root指针
b、树不为空,按二叉搜索树性质查找插入位置,插入新节点。

3.二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回,否则要删除的节点可能分下面四种情况:
a、要删除的节点无孩子节点
b、要删除的节点只有左孩子节点
c、要删除的节点只有右孩子节点
d、要删除的节点有左、右孩子节点
看起来有待删除节点有四种情况,实际情况a可以与b、c结合起来,因此真正的删除过程如下:
*有一个孩子或者无孩子的节点被删除,则让被删除节点的双亲指向被删除节点的孩子或者空——直接删除
*有两个孩子的节点被删除,则在它的右子树中寻找最小的节点,用它的值填补到删除节点中,再来处理该节点的删除问题(符合二叉搜索树,左节点<根<右节点)——替换法删除

1.3 二叉搜索树的实现
树的节点

树

完整代码:
template <class T>
struct BSTNode
{T _key;BSTNode<T>* _left;BSTNode<T>* _right;BSTNode(const T& key):_left(nullptr), _right(nullptr), _key(key){}
};template <class T>
class BSTree
{typedef BSTNode<T> Node;public:BSTree() = default;BSTree(const BSTree<T>& t){_root = Copy(t._root);}~BSTree(){Destory(_root);_root = nullptr;}bool insert(const T& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const T& key){Node* cur = _root;while (cur){if (cur->_key < key)cur = cur->_right;else if (cur->_key > key)cur = cur->_left;elsereturn cur;}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}bool Erase(const T& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 0-1个孩子的情况if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;return true;}else{// 2个孩子的情况// 右子树的最小节点作为替代节点Node* rightMinP = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;if (rightMinP->_left == rightMin)rightMinP->_left = rightMin->_right;elserightMinP->_right = rightMin->_right;delete rightMin;return true;}}}return false;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " " << endl;_InOrder(root->_right);}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);newroot->_left = Copy(root->_left);newroot->_right = Copy(root->_right);return newroot;}void Destory(Node* root){if (root == nullptr){return;}Destory(root->_left);Destory(root->_right);delete root;}Node* _root = nullptr;
};1.4 二叉搜索树的应用
1.K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
*以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
*在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型:每一个关键码key,都有与之对应的值Value,即的键值对。该种方式在现实生活中非常常见:
*比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文就构成一种键值对;
*再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是就构成一种键值对。
改造成kv结构的二叉搜索树的代码(与前面的逻辑基本上是一样的,无非就是多了一个值value)

完整代码:
using namespace std;template <class T,class V>
struct BSTNode
{T _key;V _value;BSTNode<T,V>* _left;BSTNode<T,V>* _right;BSTNode(const T& key,const V& value):_left(nullptr),_right(nullptr),_key(key),_value(value){}
};template <class T,class V>
class BSTree
{typedef BSTNode<T,V> Node;public:BSTree() = default;BSTree(const BSTree<T, V>& t){_root = Copy(t._root);}~BSTree(){Destory(_root);_root = nullptr;}bool insert(const T& key,const V& value){if (_root == nullptr){_root = new Node(key,value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key,value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const T& key){Node* cur = _root;while (cur){if (cur->_key < key)cur = cur->_right;else if (cur->_key > key)cur = cur->_left;elsereturn cur;}return nullptr;}void InOrder(){_InOrder(_root);cout << endl;}bool Erase(const T& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 删除// 0-1个孩子的情况if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;return true;}else{// 2个孩子的情况// 右子树的最小节点作为替代节点Node* rightMinP = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;if (rightMinP->_left == rightMin)rightMinP->_left = rightMin->_right;elserightMinP->_right = rightMin->_right;delete rightMin;return true;}}}return false;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " " << root->_value << endl;_InOrder(root->_right);}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key, root->_value);newroot->_left = Copy(root->_left);newroot->_right = Copy(root->_right);return newroot;}void Destory(Node* root){if (root == nullptr){return;}Destory(root->_left);Destory(root->_right);delete root;}Node* _root=nullptr;
};1.5 二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:$log_2 N$
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:$\frac{N}{2}$
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?那么AVL树和红黑树就可以上场了,但是这边就不继续讲述AVL和红黑树了。
好了,今天就到这了,我们下次见~
有问题欢迎指正批评!!!
相关文章:

C++ 二叉树
1. 二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,他或者是一棵空树,或者是具有以下性质的二叉树: ①若它的左子树不为空,则左子树上所有节点的值都小于根节点的值 ②若它的右子树不为空,则右子树上所有节…...

初探IT世界:从基础到未来
初探IT世界:从基础到未来 1. 引言 随着科技的不断发展,IT(信息技术)已经成为全球经济的支柱之一。从软件开发、网络安全到数据分析和人工智能,IT 领域为我们的日常生活提供了许多不可或缺的技术服务。无论你是初学者…...

一区黏菌算法+双向深度学习+注意力机制!SMA-BiTCN-BiGRU-Attention黏菌算法优化双向时间卷积双向门控循环单元融合注意力机制多变量回归预测
一区黏菌算法双向深度学习注意力机制!SMA-BiTCN-BiGRU-Attention黏菌算法优化双向时间卷积双向门控循环单元融合注意力机制多变量回归预测 目录 一区黏菌算法双向深度学习注意力机制!SMA-BiTCN-BiGRU-Attention黏菌算法优化双向时间卷积双向门控循环单元…...

机器翻译之Bahdanau注意力机制在Seq2Seq中的应用
目录 1.创建 添加了Bahdanau的decoder 2. 训练 3.定义评估函数BLEU 4.预测 5.知识点个人理解 1.创建 添加了Bahdanau的decoder import torch from torch import nn import dltools#定义注意力解码器基类 class AttentionDecoder(dltools.Decoder): #继承dltools.Decoder写…...

MyBatis 入门教程-搭建入门工程
Maven作为一个优秀的项目构建和管理工具,在日常的开发中被大多数开发者使用,后续的项目也是基于Maven来构建。 创建一个Maven项目 利用IDEA创建项目工具来创建一个Maven项目 添加MyBatis的依赖 这里可以从Maven仓库地址中进行查看, https://mvnrepository.com/ 从这里可…...

CVE-2024-2389 未经身份验证的命令注入
什么是 Progress Flowmon? Progress Flowmon 是一种网络监控和分析工具,可提供对网络流量、性能和安全性的全面洞察。Flowmon 将 Nette PHP 框架用于其 Web 应用程序。 未经身份验证的路由 我们开始在“AllowedModulesDecider.php”文件中枚举未经身份验证的端点,这是一个描…...

C++初阶-list用法总结
目录 1.迭代器的分类 2.算法举例 3.push_back/emplace_back 4.insert/erase函数介绍 5.splice函数介绍 5.1用法一:把一个链表里面的数据给另外一个链表 5.2 用法二:调整链表当前的节点数据 6.unique去重函数介绍 1.迭代器的分类 我们的这个迭代器…...

【智能大数据分析 | 实验一】MapReduce实验:单词计数
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈智能大数据分析 ⌋ ⌋ ⌋ 智能大数据分析是指利用先进的技术和算法对大规模数据进行深入分析和挖掘,以提取有价值的信息和洞察。它结合了大数据技术、人工智能(AI)、机器学习(ML&a…...

Git 版本控制--git restore和git reset
git restore 和 git reset 是 Git 版本控制系统中两个用于撤销更改的命令,但它们的作用范围和用途有所不同。 git restore git restore 是 Git 版本控制系统中的一个命令,用于撤销工作目录中的更改,但不影响暂存区(staging area…...
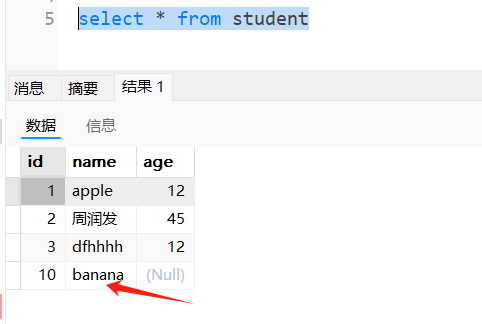
DBAPI如何实现插入数据前先判断数据是否存在,存在就更新,不存在就插入
DBAPI实现数据不存在即插入、存在即更新 场景 往数据库插入数据的时候,需要先判断一下记录是否在数据库已经存在,如果已经存在就更新记录,如果不存在,才插入数据。 实现方案 采用存储过程实现,以mysql为例子 创建存储过…...

【渗透测试】-灵当CRM系统-sql注入漏洞复现
文章目录 概要 灵当CRM系统sql注入漏洞: 具体实例: 技术名词解释 小结 概要 近期灵当CRM系统爆出sql注入漏洞,我们来进行nday复现。 灵当CRM系统sql注入漏洞: Python sqlmap.py -u "http://0.0.0.0:0000/c…...
)
c语言练习题1(数组和循环)
1实现一个对整形数组的冒泡排序 冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行的,直到没有再需要交换的元…...

实验3 Hadoop集群运行环境搭建和使用
实验3 Hadoop集群运行环境搭建和使用 一、实验介绍 本节实验旨在引导学生通过实际操作搭建一个基本的Hadoop集群,并进行基本的使用验证。实验包括在集群节点上添加域名映射以实现节点间的相互识别,配置免密SSH登录以便无密码访问各节点,安装和配置JDK以满足Hadoop的运行需求…...

前端文件上传全过程
特别说明:ui框架使用的是蚂蚁的antd 这里主要是学习前端上传接口的传递参数包括前端上传之前对于代码的整理 一、第一步将前端页面画出来 源代码: /** 费用管理 - IT费用管理 - 费用数据上传 */ import { useState } from "react"; import {…...

MySQL中的函数简单总结,以及TCL语句的简单讲解
文章目录 一、函数1、ifnull2、if3、case4、exists 存在5、字符串函数(重点)6、数学函数7、日期函数 二、TCL语句1、创建用户2、赋予权限3、修改mysql允许远程登录 一、函数 1、ifnull 当前⾯的值是null的时候,使⽤后⾯的默认值 ifnull(字段…...

GPS在Linux下的使用(war driving的前置学习)
1.ls /dev/tty* 列出所有与 tty 相关的设备文件。这些设备文件通常对应终端设备 ttyUSB0是GPS端口 2.cat /dev/ttyUSB0 用于读取并显示连接到 /dev/ttyUSB0 串口设备发送的原始数据 这种是GPS定位不全的,要拿到更开阔的地方 这种是GPS定位全的 因为会持续输出…...
开发经验总结: 读写分离简单实现
背景 使用mysql的代理中间件,某些接口如果主从同步延迟大,容易出现逻辑问题。所以程序中没有直接使用这个中间件。 依赖程序逻辑,如果有一些接口可以走读库,需要一个可以显示指定读库的方式来连接读库,降低主库的压力…...
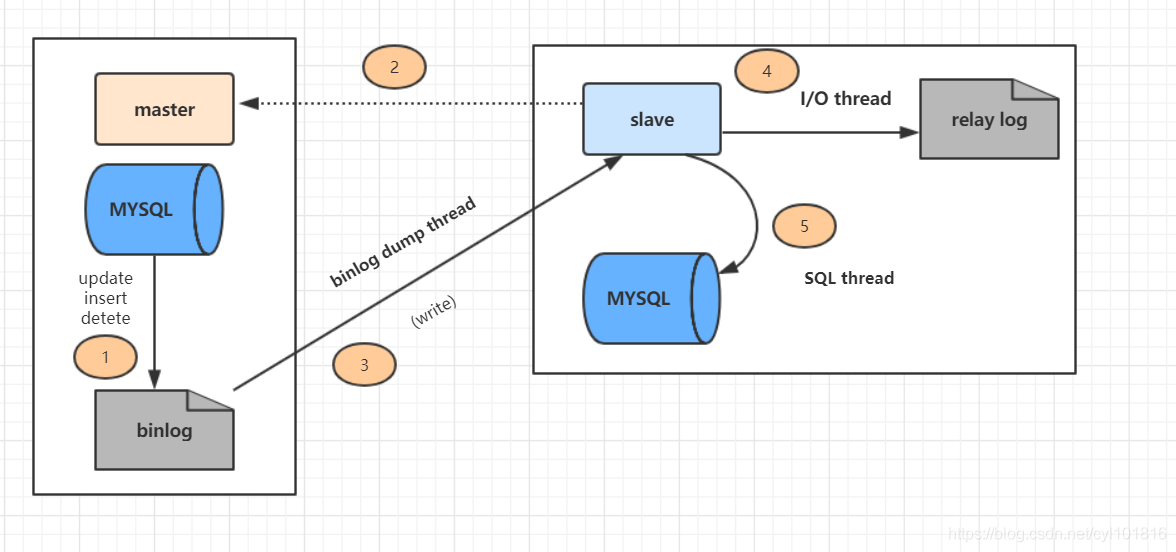
MySQL(面试题 - 同类型归纳面试题)
目录 一、MySQL 数据类型 1. 数据库存储日期格式时,如何考虑时区转换问题? 2. Blob和text有什么区别? 3. mysql里记录货币用什么字段类型比较好? 4. MySQL如何获取当前日期? 5. 你们数据库是否支持emoji表情存储&…...

【C++ Primer Plus习题】17.7
问题: 解答: #include <iostream> #include <vector> #include <string> #include <fstream> #include <algorithm>using namespace std;const int LIMIT 50;void ShowStr(const string& str); void GetStrs(ifstream& fin, vector<…...

vue3(整合版)
创建第一个vue项目 1.安装node.js cmd输入node查看是否安装成功 2.vscode开启一个终端,配置淘宝镜像 # 修改为淘宝镜像源 npm config set registry https://registry.npmmirror.com 输入如下命令创建第一个Vue项目 3.下载依赖,启动项目 访问5173端口 …...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...

【仿生机器人】刀剑神域——爱丽丝苏醒计划,需求文档
仿生机器人"爱丽丝"系统架构设计需求文档 一、硬件基础 已完成头部和颈部硬件搭建 25个舵机驱动表情系统 颈部旋转功能 眼部摄像头(视觉输入) 麦克风阵列(听觉输入) 颈部发声装置(语音输出)…...

【RabbitMQ】- Channel和Delivery Tag机制
在 RabbitMQ 的消费者代码中,Channel 和 tag 参数的存在是为了实现消息确认机制(Acknowledgment)和精细化的消息控制。 Channel 参数 作用 Channel 是 AMQP 协议的核心操作接口,通过它可以直接与 RabbitMQ 交互: 手…...
