力扣P1706全排列问题 很好的引入暴力 递归 回溯 dfs
代码思路是受一个洛谷题解里面大佬的启发。应该算是一个dfs和回溯的入门题目,很好的入门题目了下面我会先给我原题解思路我想可以很快了解这个思路。下面是我自己根据力扣大佬写的。
我会进行详细讲解并配上图辅助理解大家请往下看
#include<iostream>
#include<iomanip>
using namespace std;
int n,k;
int a[100], b[100];
void print(int n)
{for (int i = 1; i <= n; i++) {cout <<setw(5)<< a[i];}cout << endl;return;
}
void dfs(int k) {if (k == n) {print(n);return;}for (int i = 1; i <= n; i++) {if (!b[i]) {b[i] = 1;a[k + 1] = i;dfs(k + 1);b[i] = 0;}}
}
int main()
{cin >> n;dfs(0);return 0;
}

这是原题解的原代码
#include<bits/stdc++.h>
using namespace std;
int n,pd[100],used[100];//pd是判断是否用过这个数
void print()//输出函数
{int i;for(i=1;i<=n;i++)printf("%5d",used[i]);//保留五位常宽cout<<endl;
}
void dfs(int k)//深搜函数,当前是第k格
{int i;if(k==n) //填满了的时候{print();//输出当前解return;}for(i=1;i<=n;i++)//1-n循环填数{if(!pd[i])//如果当前数没有用过{pd[i]=1;//标记一下used[k+1]=i;//把这个数填入数组dfs(k+1);//填下一个pd[i]=0;//回溯}}
}
int main()
{cin>>n;dfs(0);//注意,这里是从第0格开始的!return 0;
}我一开始卡住的点是这里也是代码最最最核心的地方。我非常迷糊这里面有回溯
pd[i]=0;//回溯然后又是for循环,之后又是dfs(k+1)很明显这是递归。我不知道程序运行的顺序是什么给我绕懵逼了,昨天晚上想了一晚上。咪咪咪咪咪。
for(i=1;i<=n;i++)//1-n循环填数{if(!pd[i])//如果当前数没有用过{pd[i]=1;//标记一下used[k+1]=i;//把这个数填入数组dfs(k+1);//填下一个pd[i]=0;//回溯}}
}
重点思路总结:递归这个顺序比for循环的优先级高。通过dfs不断增加就是层数增加并且在dfs(k+1)同时进行了标记和used【K+1】计入数组,避免重复和数组填入类似剪枝和遍历,并且到达最大层数时返回并print输入结果之后回溯dfs()应为刚开始不是加到最大层数吗执行完后返回当初的dfs(2)(这里回溯其实是函数递归调用)继续循环。直到遍历所有。很巧妙,会用就行。
思路来源和思考过程
刚开始我困惑于递归这个顺序和for循环的优先级。
我用gtp作图然后又去北理工acmb站视频看了看。之后就是递归就是递推加回溯但是这个应该是计算机原理导致的。理解的话就是机器就是这样运作的,有什么调用帧啥玩意的。
如果打比方就是你可以想一想这个猴子偷桃问题,原题就是有10天每天吃二分之一+1(真能吃啊)问原来多少桃子。你把递归式子列出来然后计算机就会一个递推(形容一下你能知道我在说什么就行)到第1天吧好像是然后在回溯一直回溯然后算出结果。
其实讲到这里会的早就能听懂了。然后为了更直观大家理解我放几个图大家自行观看哈。

上面这个照片大家主要看图还有上面那几段话我觉得很好嗯说的就很好

上面这个图看看图就行我截的片段
下面的两个图是gpt辅助理解的流程大家可自行阅读理解


import pandas as pd# Data for each step of dfs for n = 3
data = [{"Step": "dfs(0)", "k": 0, "used": [None, None, None], "pd": [0, 0, 0], "Action": "Start dfs(0)"},{"Step": "dfs(0)", "k": 0, "used": [1, None, None], "pd": [1, 0, 0], "Action": "i=1, place 1, recurse dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [1, 2, None], "pd": [1, 1, 0], "Action": "i=2, place 2, recurse dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [1, 2, 3], "pd": [1, 1, 1], "Action": "i=3, place 3, recurse dfs(3)"},{"Step": "dfs(3)", "k": 3, "used": [1, 2, 3], "pd": [1, 1, 1], "Action": "Print {1, 2, 3}, backtrack to dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [1, 2, None], "pd": [1, 1, 0], "Action": "Unmark i=3, backtrack to dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [1, None, None], "pd": [1, 0, 0], "Action": "Unmark i=2, try i=3"},{"Step": "dfs(1)", "k": 1, "used": [1, 3, None], "pd": [1, 0, 1], "Action": "i=3, place 3, recurse dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [1, 3, 2], "pd": [1, 1, 1], "Action": "i=2, place 2, recurse dfs(3)"},{"Step": "dfs(3)", "k": 3, "used": [1, 3, 2], "pd": [1, 1, 1], "Action": "Print {1, 3, 2}, backtrack to dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [1, 3, None], "pd": [1, 0, 1], "Action": "Unmark i=2, backtrack to dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [1, None, None], "pd": [1, 0, 0], "Action": "Unmark i=3, backtrack to dfs(0)"},{"Step": "dfs(0)", "k": 0, "used": [None, None, None], "pd": [0, 0, 0], "Action": "Unmark i=1, try i=2"},{"Step": "dfs(0)", "k": 0, "used": [2, None, None], "pd": [0, 1, 0], "Action": "i=2, place 2, recurse dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [2, 1, None], "pd": [1, 1, 0], "Action": "i=1, place 1, recurse dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [2, 1, 3], "pd": [1, 1, 1], "Action": "i=3, place 3, recurse dfs(3)"},{"Step": "dfs(3)", "k": 3, "used": [2, 1, 3], "pd": [1, 1, 1], "Action": "Print {2, 1, 3}, backtrack to dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [2, 1, None], "pd": [1, 1, 0], "Action": "Unmark i=3, backtrack to dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [2, None, None], "pd": [0, 1, 0], "Action": "Unmark i=1, try i=3"},{"Step": "dfs(1)", "k": 1, "used": [2, 3, None], "pd": [0, 1, 1], "Action": "i=3, place 3, recurse dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [2, 3, 1], "pd": [1, 1, 1], "Action": "i=1, place 1, recurse dfs(3)"},{"Step": "dfs(3)", "k": 3, "used": [2, 3, 1], "pd": [1, 1, 1], "Action": "Print {2, 3, 1}, backtrack to dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [2, 3, None], "pd": [0, 1, 1], "Action": "Unmark i=1, backtrack to dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [2, None, None], "pd": [0, 1, 0], "Action": "Unmark i=3, backtrack to dfs(0)"},{"Step": "dfs(0)", "k": 0, "used": [None, None, None], "pd": [0, 0, 0], "Action": "Unmark i=2, try i=3"},{"Step": "dfs(0)", "k": 0, "used": [3, None, None], "pd": [0, 0, 1], "Action": "i=3, place 3, recurse dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [3, 1, None], "pd": [1, 0, 1], "Action": "i=1, place 1, recurse dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [3, 1, 2], "pd": [1, 1, 1], "Action": "i=2, place 2, recurse dfs(3)"},{"Step": "dfs(3)", "k": 3, "used": [3, 1, 2], "pd": [1, 1, 1], "Action": "Print {3, 1, 2}, backtrack to dfs(2)"},{"Step": "dfs(2)", "k": 2, "used": [3, 1, None], "pd": [1, 0, 1], "Action": "Unmark i=2, backtrack to dfs(1)"},{"Step": "dfs(1)", "k": 1, "used": [3, None, None], "pd": [0, 0, 1], "Action": "Unmark i=1, try i=2"},{"Step": "dfs(1)", "k": 1, "used": [3, 2, None], "pd": [0, 1, 1], "Action": "i=2, place 2, recurse dfs(2)"},{"Step": "dfs(2)", "k": 2
感谢观看谢谢谢谢么么么么~


相关文章:

力扣P1706全排列问题 很好的引入暴力 递归 回溯 dfs
代码思路是受一个洛谷题解里面大佬的启发。应该算是一个dfs和回溯的入门题目,很好的入门题目了下面我会先给我原题解思路我想可以很快了解这个思路。下面是我自己根据力扣大佬写的。 我会进行详细讲解并配上图辅助理解大家请往下看 #include<iostream> #inc…...

使用Python Pandas导入数据库和文件数据
大家好,在数据分析过程中,数据的导入是第一步,也是最重要的一步。Python的Pandas提供了强大的数据读取功能,支持从多种数据源导入数据,包括CSV、Excel、JSON、SQL数据库、网页等。Pandas库不仅能够处理常见的文件格式&…...

lef 中antenna解释
这些规则主要涉及集成电路设计中的天线效应(Antenna Effect)和通孔(Via)设计规则。 ANTENNAAREADIFFREDUCEPWL 这条规则指定了一个分段线性函数,用于根据连接到切割层的扩散区面积来计算cut_area的缩减因子。扩散区面积值应从0开始单调增加。如果没有定义此规则,PAR(mi)方程中的…...
初试Bootstrap前端框架
文章目录 一、Bootstrap概述二、Bootstrap实例1、创建网页2、编写代码3、代码说明4、浏览网页,查看结果5、登录按钮事件处理6、浏览网页,查看结果 三、实战小结 一、Bootstrap概述 大家好,今天我们将一起学习一个非常流行的前端框架——Boot…...

mysql数据库:超键、候选键、主键与外键
mysql数据库:超键、候选键、主键与外键 1、超键(Superkey)2、候选键(Candidate Key)3、主键(Primary Key)4、外键(Foreign Key) 💖The Begin💖点点…...
音频转MP3格式困难?如何轻松实现wav转mp3?
格式多样化为我们带来了灵活性和创意的无限可能,但同时,不同格式间的转换也成为了不少用户面临的难题。尤其是当你手握珍贵的WAV音频文件,却希望它们能在更多设备上流畅播放或节省存储空间时,wav转mp3的需求便应运而生。WAV以其无…...

基于vue框架的大连盐业有限公司生产管理系统的设计与实现3hk5y(程序+源码+数据库+调试部署+开发环境)系统界面在最后面。
系统程序文件列表 项目功能:计划员,工艺员,生产建模,生产计划,生产信息,生产监视,工艺质量,盐政信息 开题报告内容 一、引言 随着信息技术的飞速发展和市场竞争的日益激烈,传统盐业企业如大连盐业有限公司正面临着转型升级的迫切需求。传统管理模式下…...

《深入理解JAVA虚拟机(第2版)》- 第13章 - 学习笔记【终章】
第13章 线程安全与锁优化 13.1 概述 面向过程的编程思想 将数据和过程独立分开,数据是问题空间中的客体,程序代码是用来处理数据的,这种站在计算机角度来抽象和解决问题的思维方式,称为面向对象的编程思想。 面向对象的编程思想…...
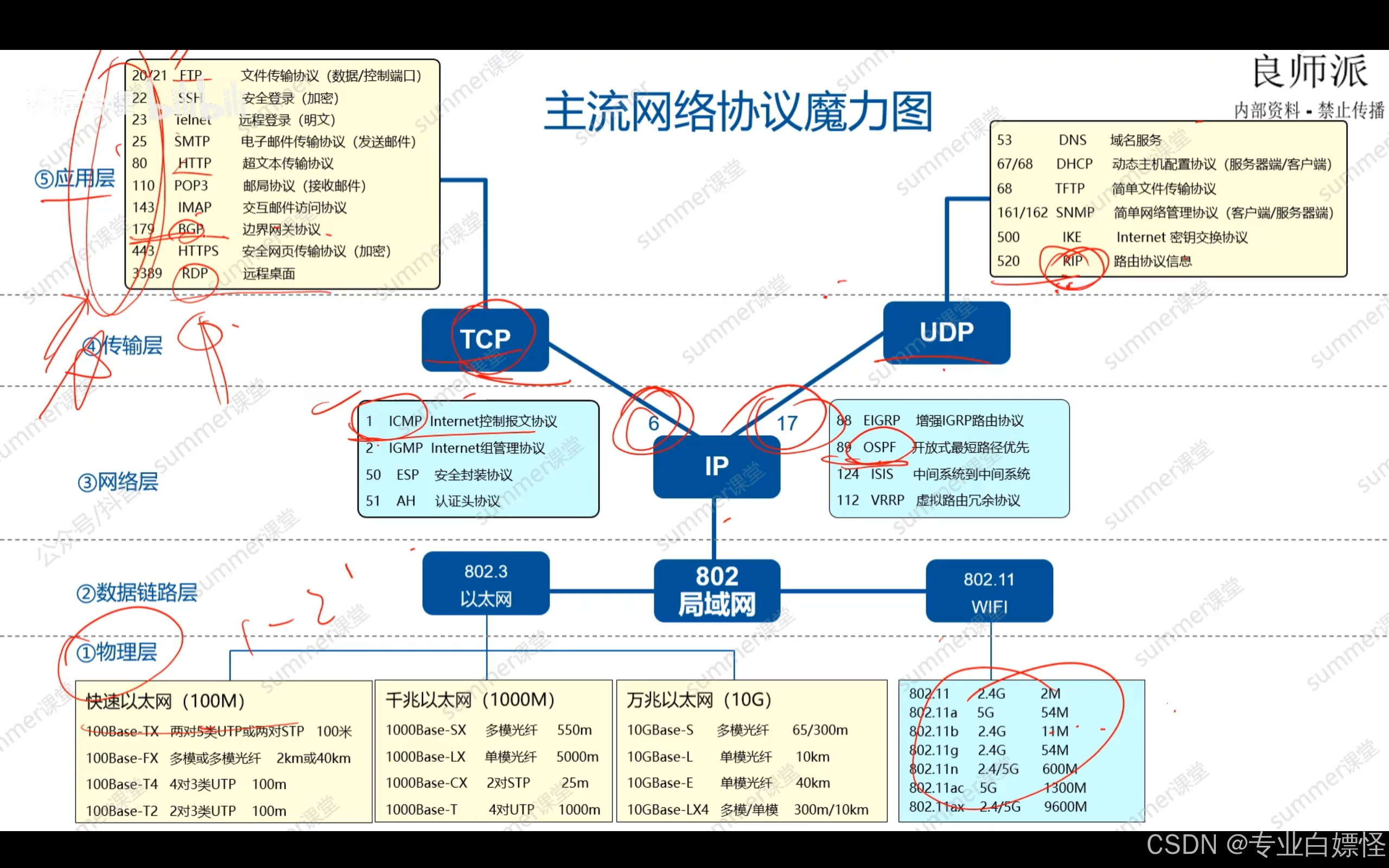
网络工程师学习笔记——网络互连与互联网(三)
TCP三次握手 建立TCP连接是通过三次握手实现的,采用三报文握手主要是为了防止已失效的连接请求报文突然又传送到了,因而产生错误 主动发起TCP连接建立的称为客户端 被动等待的为TCP服务器,二者之间需要交换三个TCP报文段 首先是客户端主动…...

【Tomcat】常见面试题整理 共34题
文章目录 1. 简述什么是Tomcat?2. Tomcat的缺省端口是多少,怎么修改?3. 简述Tomcat 目录结构及作用4. 简述Tomcat有几种部署方式?5. 简述Tomcat容器是如何创建servlet类实例?6. Tomcat有哪几种Connector运行模式&#…...
到时间没回家又不接电话?如何迅速确定孩子的位置?
当孩子未按时回家且无法通过电话联系时,家长往往会感到焦虑。此时,如何迅速确定孩子的位置成为许多家长迫切需要解决的问题。 利用智能手机定位技术是最常见的方法之一。大多数智能手机都内置GPS定位功能,通过“查找设备”应用,家…...

接口自动化--commons内容详解-02
上篇文章主要讲解了接口自动化主要架构框架,这篇文庄主要讲解commons中的内容 1. requests_utils.py 首先讲解这个工具类,主要是因为在接口自动化中,基本都有的接口都是发送请求,获取响应结果,唯一不同的是࿰…...

WanFangAi论文写作研究生论文写作神器在线生成真实数据,标注参考文献位置,表格公式代码流程图查重20以内,研究生论文写作技巧
WanFangAi是一个专业的学术论文辅助平台,它提供了一系列工具来帮助用户提升论文写作的效率和质量。以下是WanFangAi的一些核心功能:1.主题探索与文献搜索:用户可以输入关键词和研究领域,WanFangAi会迅速推荐合适的论文主题并提供相关的文献搜索服务。系统…...
 按键盘无效)
cv2.waitkey(30) 按键盘无效
cv2.imshow("detection", color_image) # 窗口显示,显示名为 Capture_Videok cv2.waitKey(100) & 0xFF # 每帧数据延时 1ms,延时不能为 0,否则读取的结果会是静态帧 if k ord(s): # 键盘按一下s, 保存当前照片和机械臂位姿…...

【洛谷】P10417 [蓝桥杯 2023 国 A] 第 K 小的和 的题解
【洛谷】P10417 [蓝桥杯 2023 国 A] 第 K 小的和 的题解 题目传送门 题解 CSP-S1 补全程序,致敬全 A 的答案,和神奇的预言家。 写一下这篇的题解说不定能加 CSP 2024 的 RP 首先看到 k k k 这么大的一个常数,就想到了二分。然后写一个判…...

Ubuntu24.04 安装ssh开启22端口及允许root用户远程登录
1、安装openssh-server插件开启22端口访问 # 安装ssh会默认启动服务并开启22端口 apt update apt install openssh-server 2、开启root用户远程访问 激活root用户,设置root用户登录密码 hunterlocalhost:/$ sudo passwd root New password: Retype new password…...

STM32基础学习笔记-DHT11单总线协议面试基础题7
第七章、DHT11: 单总线协!议 常见问题 1、DHT11是什么 ?有什么特性 ? 2、单总线协议是什么 ?原理 ?DHT11的单总线协议的组成 ? ## 1、DHT11定义 单总线协议是一种用于在多个设备之间进行通信的协议,所有…...
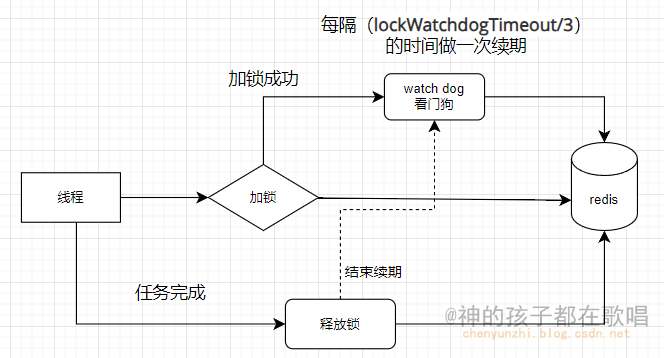
Redisson分布式锁的概念和使用
Redisson分布式锁的概念和使用 一 简介1.1 什么是分布式锁?1.2 Redisson分布式锁的原理1.3 Redisson分布式锁的优势1.4 Redisson分布式锁的应用场景 二 案例2.1 锁竞争案例2.2 看门狗案例2.3 参考文章 前言 这是我在这个网站整理的笔记,有错误的地方请指出ÿ…...

uniapp小程序持续获取用户位置信息,后台位置获取
做一个小程序持续获取用户位置信息的功能,即使小程序切换到后台也能继续获取,getLocation这个api只有小程序在前台才能获取位置,所以不用这个 先申请一个腾讯地图key 在uniapp项目配置源码视图里加上这个代码 先获取权限,再开启…...
优化算法(五)—梯度下降算法(附MATLAB程序)
梯度下降算法(Gradient Descent)是一种常用的优化算法,用于寻找函数的局部最小值。它通过沿着函数梯度的反方向迭代地调整变量,以逐步找到最优解。梯度下降广泛应用于机器学习和深度学习中,特别是在训练模型时优化损失…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
