LeetCode练习七:动态规划上:线性动态规划
文章目录
- 一、 动态规划基础知识
- 1.1 动态规划简介
- 1.2 动态规划的特征
- 1.2.1 最优子结构性质
- 1.2.2 重叠子问题性质
- 1.2.3 无后效性
- 1.3 动态规划的基本思路
- 1.4 动态规划基础应用
- 1.4.1 斐波那契数
- 1.4.2 爬楼梯
- 1.4.3 不同路径
- 1.5 个人总结
- 二、记忆化搜索
- 2.1 记忆化搜索简介
- 2.2 记忆化搜索与递推的区别
- 2.3 记忆化搜索的应用
- 2.3.1 目标和
- 2.3.2 第 N 个泰波那契数
- 三、线性动态规划简介
- 3.1 单串线性 DP 问题
- 3.1.1 最长递增子序列
- 3.1.2 最大子数组和
- 3.1.2.1 动态规划
- 3.1.2.2 动态规划+滚动数组
- 3.1.3 最长的斐波那契子序列的长度
- 3.1.3.1 暴力枚举(超时)
- 3.1.3.2 哈希表
- 3.1.3.3 动态规划 + 哈希表
- 3.2 双串线性 DP 问题
- 3.2.1 最长公共子序列
- 3.2.2 最长重复子数组
- 3.3.3 编辑距离
- 3.3 矩阵线性 DP问题
- 3.3.1 最小路径和
- 3.3.2最大正方形
- 3.4无串线性 DP 问题
- 3.4.1 整数拆分
- 3.4.2 只有两个键的键盘
- 3.5 线性 DP 题目大全
参考《OI Wiki动态规划》、《算法通关手册》动态规划篇
一、 动态规划基础知识
1.1 动态规划简介
动态规划(Dynamic Programming):简称 DP,是一种通过把原问题分解为相对简单的子问题的方式而求解复杂问题的方法。
动态规划方法与分治算法类似,却又不同于分治算法。
「动态规划的核心思想」是:
- 把「原问题」分解为「若干个重叠的子问题」,每个子问题的求解过程都构成一个 「阶段」。在完成一个阶段的计算之后,动态规划方法才会执行下一个阶段的计算。
- 在求解子问题的过程中,按照自底向上的顺序求解出「子问题的解」,把结果存储在表格中,当需要再次求解此子问题时,直接从表格中查询该子问题的解,从而避免了大量的重复计算。
「动态规划方法与分治算法的不同点」在于:
- 适用于动态规划求解的问题,在分解之后得到的子问题往往是相互联系的,会出现若干个重叠子问题。
- 使用动态规划方法会将这些重叠子问题的解保存到表格里,供随后的计算查询使用,从而避免大量的重复计算。
1.2 动态规划的特征
能够使用动态规划方法解决的问题必须满足下面三个特征:「最优子结构性质」、「重叠子问题性质」和「无后效性」。
1.2.1 最优子结构性质
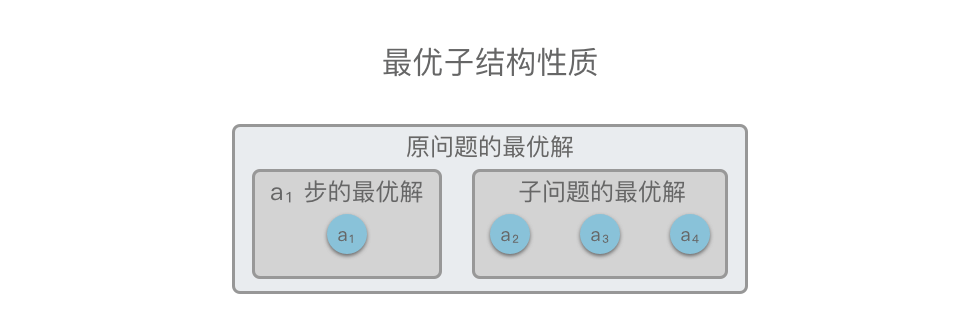
「最优子结构」:指的是一个问题的最优解包含其子问题的最优解。
举个例子,如下图所示,原问题 S={a1,a2,a3,a4}S = \lbrace a_1, a_2, a_3, a_4 \rbraceS={a1,a2,a3,a4},在 a1a_1a1 步我们选出一个当前最优解之后,问题就转换为求解子问题 S子问题={a2,a3,a4}S_{子问题} = \lbrace a_2, a_3, a_4 \rbraceS子问题={a2,a3,a4}。如果原问题 SSS 的最优解可以由「第 a1a_1a1 步得到的局部最优解」和「 S子问题S_{子问题}S子问题 的最优解」构成,则说明该问题满足最优子结构性质。
也就是说,如果原问题的最优解包含子问题的最优解,则说明该问题满足最优子结构性质。
1.2.2 重叠子问题性质
「重叠子问题性质」:指的是在求解子问题的过程中,有大量的子问题是重复的,一个子问题会在下一阶段的决策中可能会被多次用到。如果有大量重复的子问题,那么只需要对求解一次,然后用表格将结果存储下来,以后使用时可以直接查询,不需要再次求解。
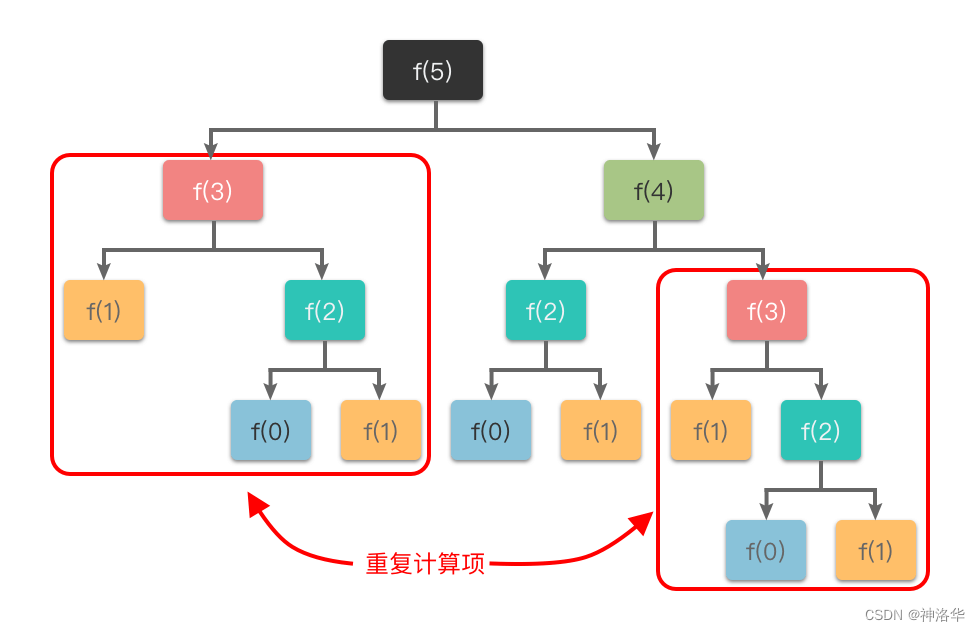
举个例子,比如斐波那契数列的定义是:f(1) = 1, f(2) = 2, f(n) = f(n - 1) + f(n - 2)。对应的递推过程如下图所示,其中 f(1)、f(2)、f(3)、f(4) 都进行了多次重复计算。而如果我们在第一次计算 f(1)、f(2)、f(3)、f(4) 时就将其结果存入表格,则再次使用时可以直接查询,从而避免重复求解相同的子问题,提升效率。
1.2.3 无后效性
「无后效性」:指的是子问题的解(状态值)只与之前阶段有关,而与后面阶段无关。当前阶段的若干状态值一旦确定,就不再改变,不会再受到后续阶段决策的影响。换句话说,一旦某一个子问题的求解结果确定以后,就不会再被修改。
其实我们也可以把动态规划方法的求解过程,看做是有向无环图的最长(最短)路的求解过程。每个状态对应有向无环图上的一个节点,决策对应图中的一条有向边。
如果一个问题具有「后效性」,则可能需要将其转化或者逆向求解来消除后效性,然后才可以使用动态规划方法。
1.3 动态规划的基本思路
如下图所示,我们在使用动态规划方法解决某些最优化问题时,可以将解决问题的过程按照一定顺序(时间顺序、空间顺序或其他顺序)分解为若干个相互联系的「阶段」。然后按照顺序对每一个阶段做出「决策」,这个决策既决定了本阶段的效益,也决定了下一阶段的初始状态。依次做完每个阶段的决策之后,就得到了一个整个问题的决策序列。
这样就将一个原问题分解为了一系列的子问题,然后通过逐步求解从而获得最终结果。
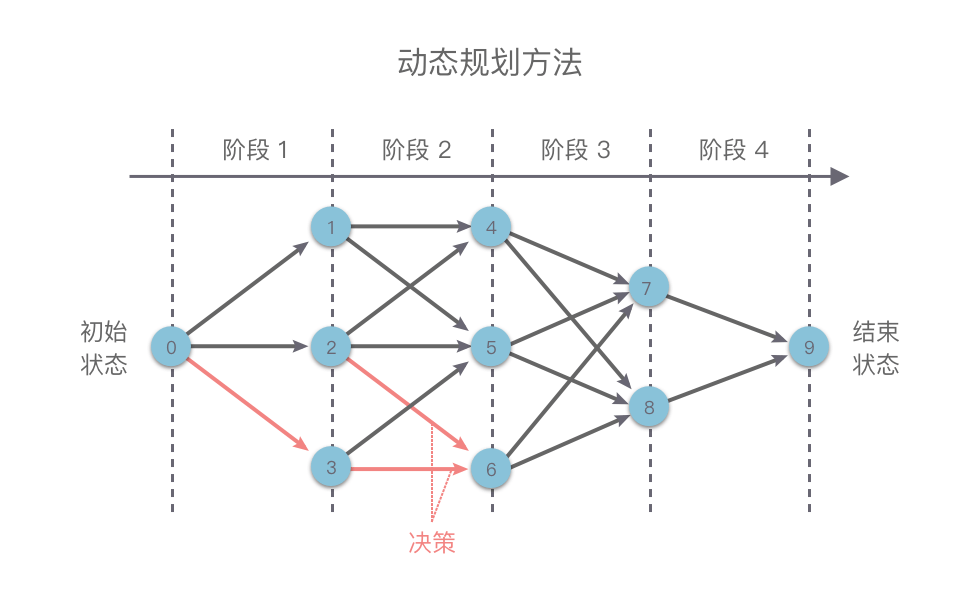
这种前后关联、具有链状结构的多阶段进行决策的问题也叫做「多阶段决策问题」。通常我们使用动态规划方法来解决多阶段决策问题,其基本思路如下:
- 划分阶段:将原问题按顺序(时间顺序、空间顺序或其他顺序)分解为若干个相互联系的「阶段」。划分后的阶段⼀定是有序或可排序的,否则问题⽆法求解。
- 这里的「阶段」指的是⼦问题的求解过程。每个⼦问题的求解过程都构成⼀个「阶段」,在完成前⼀阶段的求解后才会进⾏后⼀阶段的求解。
- 定义状态:将和子问题相关的某些变量(位置、数量、体积、空间等等)作为一个「状态」表示出来。状态的选择要满⾜⽆后效性。
- 一个「状态」对应一个或多个子问题,所谓某个「状态」下的值,指的就是这个「状态」所对应的子问题的解。
- 状态转移:根据「上一阶段的状态」和「该状态下所能做出的决策」,推导出「下一阶段的状态」。或者说根据相邻两个阶段各个状态之间的关系,确定决策,然后推导出状态间的相互转移方式(即「状态转移方程」)。
- 初始条件和边界条件:根据问题描述、状态定义和状态转移方程,确定初始条件和边界条件。
- 最终结果:确定问题的求解目标,然后按照一定顺序求解每一个阶段的问题。最后根据状态转移方程的递推结果,确定最终结果。
1.4 动态规划基础应用
动态规划相关的问题往往灵活多变,思维难度大,没有特别明显的套路,并且经常会在各类算法竞赛和面试中出现。
动态规划问题的关键点在于「如何状态设计」和「推导状态转移条件」,还有各种各样的「优化方法」。这类问题一定要多练习、多总结,只有接触的题型多了,才能熟练掌握动态规划思想。
下面来介绍几道关于动态规划的基础题目。
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0509 | 斐波那契数 | Python | 数组 | 简单 |
| 0070 | 爬楼梯 | Python | 动态规划 | 简单 |
| 0062 | 不同路径 | Python | 数组、动态规划 | 中等 |
1.4.1 斐波那契数
509. 斐波那契数 - 力扣
给定一个整数 n。:计算第 n 个斐波那契数。其中,斐波那契数列的定义如下:
f(0) = 0, f(1) = 1。f(n) = f(n - 1) + f(n - 2),其中n > 1。
解题思路
-
划分阶段:按照整数顺序进行阶段划分,将其划分为整数
0~n。 -
定义状态:定义状态
dp[i]为:第i个斐波那契数。 -
状态转移方程
根据题目中所给的斐波那契数列的定义f(n) = f(n - 1) + f(n - 2),则直接得出状态转移方程为dp[i] = dp[i - 1] + dp[i - 2]。 -
初始条件
根据题目中所给的初始条件f(0) = 0, f(1) = 1确定动态规划的初始条件,即dp[0] = 0, dp[1] = 1。 -
最终结果
根据状态定义,最终结果为dp[n],即第n个斐波那契数为dp[n]。
class Solution:def fib(self, n: int) -> int:if n <= 1:return ndp = [0 for _ in range(n + 1)]dp[0] = 0dp[1] = 1for i in range(2, n + 1):dp[i] = dp[i - 2] + dp[i - 1]return dp[n]
复杂度分析
- 时间复杂度:O(n)O(n)O(n)。一重循环遍历的时间复杂度为 O(n)O(n)O(n)。
- 空间复杂度:O(n)O(n)O(n)。
- 用到了一维数组保存状态,所以总体空间复杂度为 O(n)O(n)O(n)。
- 因为
dp[i]的状态只依赖于dp[i - 1]和dp[i - 2],所以可以使用3个变量来分别表示dp[i]、dp[i - 1]、dp[i - 2],从而将空间复杂度优化到 O(1)O(1)O(1)。
1.4.2 爬楼梯
70. 爬楼梯 - 力扣
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。现在给定一个整数 n。请计算出有多少种不同的方法可以爬到楼顶。
- 1≤n≤451 \le n \le 451≤n≤45。
示例:
输入 n = 3
输出 3
解释 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
解题思路
-
划分阶段
我们按照台阶的阶层划分阶段,将其划分为0~n阶。 -
定义状态
定义状态dp[i]为:爬到第i阶台阶的方案数。 -
状态转移方程
根据题目大意,每次只能爬1或2个台阶。则第i阶楼梯只能从第i - 1阶向上爬1阶上来,或者从第i - 2阶向上爬2阶上来。所以可以推出状态转移方程为dp[i] = dp[i - 1] + dp[i - 2]。 -
初始条件
- 第
0层台阶方案数:可以看做1种方法(从0阶向上爬0阶),即dp[1] = 1。 - 第
1层台阶方案数:1种方法(从0阶向上爬1阶),即dp[1] = 1。 - 第
2层台阶方案数:2中方法(从0阶向上爬2阶,或者从1阶向上爬1阶)。
- 第
-
最终结果
根据状态定义,最终结果为dp[n],即爬到第n阶台阶(即楼顶)的方案数为dp[n]。
虽然这道题跟上一道题的状态转移方程都是 dp[i] = dp[i - 1] + dp[i - 2],但是两道题的考察方式并不相同,一定程度上也可以看出来动态规划相关题目的灵活多变。
代码
class Solution:def climbStairs(self, n: int) -> int:dp = [0 for _ in range(n + 1)]dp[0] = 1dp[1] = 1for i in range(2, n + 1):dp[i] = dp[i - 1] + dp[i - 2]return dp[n]
复杂度分析
- 时间复杂度:O(n)O(n)O(n)。一重循环遍历的时间复杂度为 O(n)O(n)O(n)。
- 空间复杂度:O(n)O(n)O(n)。
- 用到了一维数组保存状态,所以总体空间复杂度为 O(n)O(n)O(n)。
- 因为
dp[i]的状态只依赖于dp[i - 1]和dp[i - 2],所以可以使用3个变量来分别表示dp[i]、dp[i - 1]、dp[i - 2],从而将空间复杂度优化到 O(1)O(1)O(1)。
1.4.3 不同路径
62. 不同路径 - 力扣
给定两个整数 m 和 n,代表大小为 m * n 的棋盘, 一个机器人位于棋盘左上角的位置,机器人每次只能向右、或者向下移动一步。要求计算出机器人从棋盘左上角到达棋盘右下角一共有多少条不同的路径。
- 1≤m,n≤1001 \le m, n \le 1001≤m,n≤100。
- 题目数据保证答案小于等于 2∗1092 * 10^92∗109。
示例:
输入 m = 3, n = 7
输出 28
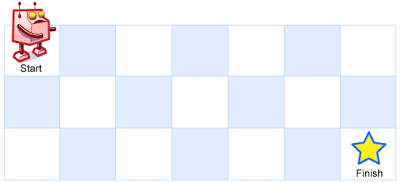
解题思路
-
划分阶段
按照路径的结尾位置(行位置、列位置组成的二维坐标)进行阶段划分。 -
定义状态
定义状态dp[i][j]为:从左上角到达(i, j)位置的路径数量。 -
状态转移方程
因为我们每次只能向右、或者向下移动一步,因此想要走到(i, j),只能从(i - 1, j)向下走一步走过来;或者从(i, j - 1)向右走一步走过来。所以可以写出状态转移方程为:dp[i][j] = dp[i - 1][j] + dp[i][j - 1],此时i > 0,j > 0。 -
初始条件
- 从左上角走到
(0, 0)只有一种方法,即dp[0][0] = 1。 - 第一行元素只有一条路径(即只能通过前一个元素向右走得到),所以
dp[0][j] = 1。 - 同理,第一列元素只有一条路径(即只能通过前一个元素向下走得到),所以
dp[i][0] = 1。
- 从左上角走到
-
最终结果
根据状态定义,最终结果为dp[m - 1][n - 1],即从左上角到达右下角(m - 1, n - 1)位置的路径数量为dp[m - 1][n - 1]。
代码
class Solution(object):def uniquePaths(self, m, n):""":type m: int:type n: int:rtype: int"""# 使用一个二维列表进行存储,dp[i][j]表示i行j列有多少种路径dp=[[0]*n for _ in range(m)]for i in range(m):dp[i][0]=1 # 第一列路径为1for j in range(n):dp[0][j]=1 # 第一行路径为1if i>0 and j>0: # 第一行第一列之外的位置,路径数为上方位置和左边位置的路径数之和dp[i][j]=dp[i-1][j]+dp[i][j-1]return dp[m-1][n-1]
复杂度分析
- 时间复杂度:O(m∗n)O(m * n)O(m∗n)。初始条件赋值的时间复杂度为 O(m+n)O(m + n)O(m+n),两重循环遍历的时间复杂度为 O(m∗n)O(m * n)O(m∗n),所以总体时间复杂度为 O(m∗n)O(m * n)O(m∗n)。
- 空间复杂度:
- O(m∗n)O(m * n)O(m∗n)。用到了二维数组保存状态,所以总体空间复杂度为 O(m∗n)O(m * n)O(m∗n)。
- 因为
dp[i][j]的状态只依赖于上方值dp[i - 1][j]和左侧值dp[i][j - 1],而我们在进行遍历时的顺序刚好是从上至下、从左到右。所以我们可以使用长度为m的一维数组来保存状态,从而将空间复杂度优化到 O(m)O(m)O(m)。
1.5 个人总结
-
枚举算法(Enumeration Algorithm):即穷举法,指的是按照问题本身的性质,一一列举出该问题所有可能的解,并在逐一列举的过程中,将它们逐一与目标状态进行比较以得出满足问题要求的解。在列举的过程中,既不能遗漏也不能重复。
-
分治算法(Divide and Conquer):「分而治之」,把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
-
递归(Recursion):通过重复将原问题分解为同类的子问题而解决的方法。在绝大数编程语言中,可以通过在函数中再次调用函数自身的方式来实现递归。
-
动态规划(Dynamic Programming):
- 类似分治,将复杂问题,分解为更简单的子问题进行求解(划分阶段);
- 类似枚举,会计算出每个阶段的结果(子问题最优解),但是下一阶段的结果是根据上一阶段的结果算出,而不是直接从头计算,所以存在状态转移,提高效率
- 重复调用:根据上一阶段的结果来计算下一阶段的结果,所以使用动态规划方法会将各阶段的解保存到表格里,供随后的计算查询使用,从而避免大量的重复计算。
二、记忆化搜索
2.1 记忆化搜索简介
记忆化搜索(Memoization Search):是一种通过存储已经遍历过的状态信息,从而避免对同一状态重复遍历的搜索算法。
记忆化搜索是动态规划的一种实现方式。在记忆化搜索中,当算法需要计算某个子问题的结果时,它首先检查是否已经计算过该问题。如果已经计算过,则直接返回已经存储的结果;否则,计算该问题,并将结果存储下来以备将来使用。
举个例子,比如「斐波那契数列」的定义是:f(0)=0,f(1)=1,f(n)=f(n−1)+f(n−2)f(0) = 0, f(1) = 1, f(n) = f(n - 1) + f(n - 2)f(0)=0,f(1)=1,f(n)=f(n−1)+f(n−2)。如果我们使用递归算法求解第 nnn 个斐波那契数,则对应的递推过程如下:
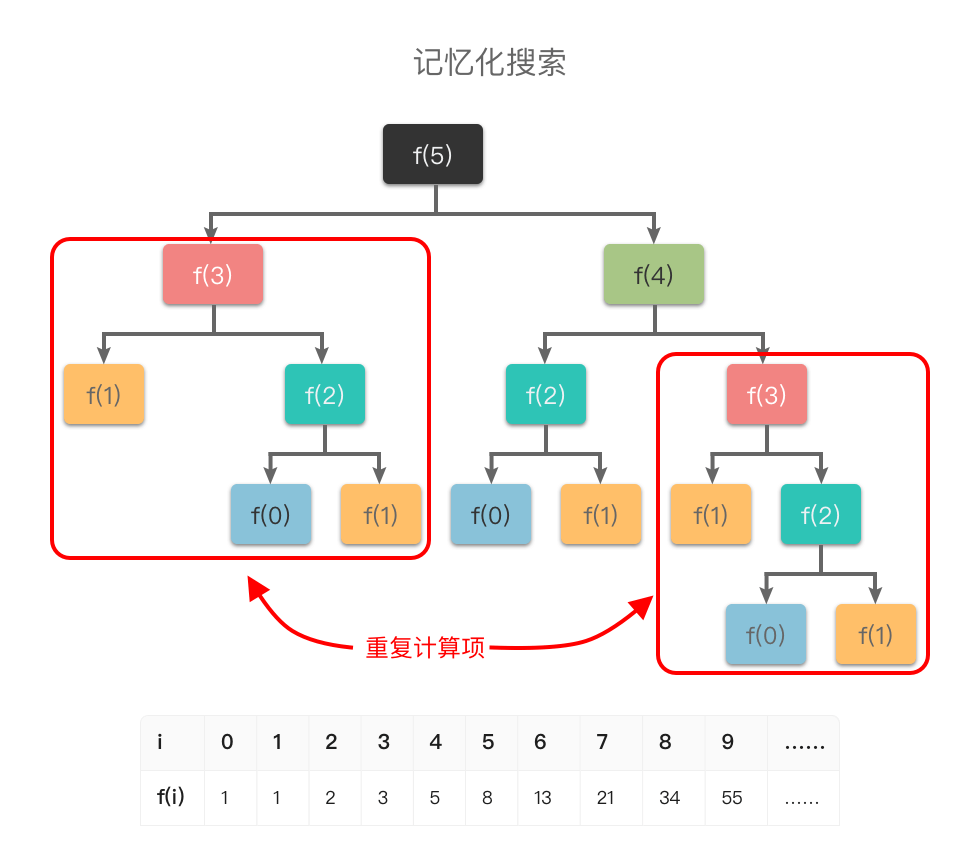
从图中可以看出:如果使用普通递归算法,想要计算 f(5)f(5)f(5),需要先计算 f(3)f(3)f(3) 和 f(4)f(4)f(4),而在计算 f(4)f(4)f(4) 时还需要计算 f(3)f(3)f(3)。这样 f(3)f(3)f(3) 就进行了多次计算,同理 f(0)f(0)f(0)、f(1)f(1)f(1)、f(2)f(2)f(2) 都进行了多次计算,从而导致了重复计算问题。
为了避免重复计算,在递归的同时,我们可以使用一个缓存(数组或哈希表)来保存已经求解过的 f(k)f(k)f(k) 的结果。如上图所示,当递归调用用到 f(k)f(k)f(k) 时,先查看一下之前是否已经计算过结果,如果已经计算过,则直接从缓存中取值返回,而不用再递推下去,这样就避免了重复计算问题。
我们在使用记忆化搜索解决问题的时候,其基本步骤如下:
- 写出问题的动态规划「状态」和「状态转移方程」。
- 定义一个缓存(数组或哈希表),用于保存子问题的解。
- 定义一个递归函数,用于解决问题。在递归函数中,首先检查缓存中是否已经存在需要计算的结果,如果存在则直接返回结果,否则进行计算,并将结果存储到缓存中,再返回结果。
- 在主函数中,调用递归函数并返回结果。
使用「记忆化搜索」方法解决斐波那契数列的代码如下:
class Solution:def fib(self, n: int) -> int:# 使用数组保存已经求解过的 f(k) 的结果memo = [0 for _ in range(n + 1)]return self.my_fib(n, memo)def my_fib(self, n: int, memo: List[int]) -> int:if n < 2:return n# 已经计算过结果if memo[n] != 0:return memo[n]# 没有计算过结果memo[n] = self.my_fib(n - 1, memo) + self.my_fib(n - 2, memo)return memo[n]
2.2 记忆化搜索与递推的区别
「记忆化搜索」与「递推」都是动态规划的实现方式,但是两者之间有一些区别。
-
记忆化搜索:「自顶向下」的解决问题,采用自然的递归方式编写过程,在过程中会保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
- 优点:代码清晰易懂,可以有效的处理一些复杂的状态转移方程。有些状态转移方程是非常复杂的,使用记忆化搜索可以将复杂的状态转移方程拆分成多个子问题,通过递归调用来解决。
- 缺点:可能会因为递归深度过大而导致栈溢出问题。
- 适用场景:题的状态转移方程比较复杂,递推关系不是很明确;问题适合转换为递归形式,并且递归深度不会太深。
-
递推:「自底向上」的解决问题,采用循环的方式编写过程,在过程中通过保存每个子问题的解(通常保存在一个数组或哈希表中)来避免重复计算。
- 优点:避免了深度过大问题,不存在栈溢出问题。计算顺序比较明确,易于实现。
- 缺点:无法处理一些复杂的状态转移方程。有些状态转移方程非常复杂,如果使用递推方法来计算,就会导致代码实现变得非常困难。
- 适用场景:问题的状态转移方程比较简单,递归关系比较明确;问题不太适合转换为递归形式,或者递归深度过大容易导致栈溢出。
2.3 记忆化搜索的应用
2.3.1 目标和
494. 目标和 - 力扣
给定一个整数数组 numsnumsnums 和一个整数 targettargettarget。数组长度不超过 202020。向数组中每个整数前加 + 或 -。然后串联起来构造成一个表达式。返回通过上述方法构造的、运算结果等于 targettargettarget 的不同表达式数目。
说明:
- 1≤nums.length≤201 \le nums.length \le 201≤nums.length≤20。
- 0≤nums[i]≤10000 \le nums[i] \le 10000≤nums[i]≤1000。
- 0≤sum(nums[i])≤10000 \le sum(nums[i]) \le 10000≤sum(nums[i])≤1000。
- −1000≤target≤1000-1000 \le target \le 1000−1000≤target≤1000。
示例:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
思路 1:深度优先搜索(超时)
使用深度优先搜索对每位数字进行 + 或者 -,具体步骤如下:
- 定义从位置 000、和为 000 开始,到达数组尾部位置为止,和为 targettargettarget 的方案数为
dfs(0, 0)。 - 下面从位置 000、和为 000 开始,以深度优先搜索遍历每个位置。
- 如果当前位置 iii 到达最后一个位置 sizesizesize:
- 如果和
cur_sum等于目标和 targettargettarget,则返回方案数 111。 - 如果和
cur_sum不等于目标和 targettargettarget,则返回方案数 000。
- 如果和
- 递归搜索 i+1i + 1i+1 位置,和为
cur_sum - nums[i]的方案数。 - 递归搜索 i+1i + 1i+1 位置,和为
cur_sum + nums[i]的方案数。 - 将 4 ~ 5 两个方案数加起来就是当前位置 iii、和为
cur_sum的方案数,返回该方案数。 - 最终方案数为
dfs(0, 0),将其作为答案返回即可。
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:size = len(nums)def dfs(i, cur_sum):if i == size:if cur_sum == target:return 1else:return 0ans = dfs(i + 1, cur_sum - nums[i]) + dfs(i + 1, cur_sum + nums[i])return ansreturn dfs(0, 0)
- 时间复杂度:O(2n)O(2^n)O(2n)。其中 nnn 为数组 numsnumsnums 的长度。
- 空间复杂度:O(n)O(n)O(n)。递归调用的栈空间深度不超过 nnn。
思路 2:记忆化搜索
在思路 1 中我们单独使用深度优先搜索对每位数字进行 + 或者 - 的方法超时了。所以我们考虑使用记忆化搜索的方式,避免进行重复搜索。
这里我们使用哈希表 tabletabletable 记录遍历过的位置 iii 及所得到的的当前和cur_sum 下的方案数,来避免重复搜索。具体步骤如下:
- 定义从位置 000、和为 000 开始,到达数组尾部位置为止,和为 targettargettarget 的方案数为
dfs(0, 0)。 - 下面从位置 000、和为 000 开始,以深度优先搜索遍历每个位置。
- 如果当前位置 iii 遍历完所有位置:
- 如果和
cur_sum等于目标和 targettargettarget,则返回方案数 111。 - 如果和
cur_sum不等于目标和 targettargettarget,则返回方案数 000。
- 如果和
- 如果当前位置 iii、和为
cur_sum之前记录过(即使用 tabletabletable 记录过对应方案数),则返回该方案数。 - 如果当前位置 iii、和为
cur_sum之前没有记录过,则:- 递归搜索 i+1i + 1i+1 位置,和为
cur_sum - nums[i]的方案数。 - 递归搜索 i+1i + 1i+1 位置,和为
cur_sum + nums[i]的方案数。 - 将上述两个方案数加起来就是当前位置 iii、和为
cur_sum的方案数,将其记录到哈希表 tabletabletable 中,并返回该方案数。
- 递归搜索 i+1i + 1i+1 位置,和为
- 最终方案数为
dfs(0, 0),将其作为答案返回
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:size = len(nums)table = dict()def dfs(i, cur_sum):if i == size:if cur_sum == target:return 1else:return 0if (i, cur_sum) in table:return table[(i, cur_sum)]cnt = dfs(i + 1, cur_sum - nums[i]) + dfs(i + 1, cur_sum + nums[i])table[(i, cur_sum)] = cntreturn cntreturn dfs(0, 0)
- 时间复杂度:O(2n)O(2^n)O(2n)。其中 nnn 为数组 numsnumsnums 的长度。
- 空间复杂度:O(n)O(n)O(n)。递归调用的栈空间深度不超过 nnn。
思路3:动态规划
此题也可使用动态规划求解,参考《『 一文搞懂 0-1背包问题 』记忆化搜索、动态规划 + 空间优化》
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:''' pos + neg = total '''''' pos - neg = target '''total = sum(nums)if abs(target) > total: # target可能为负return 0if (total + target) % 2 == 1: # 不能被2整除【对应于pos不是整数】return 0'''【0/1背包】:从nums中选出数字组成pos或neg'''pos = (total + target) // 2neg = (total - target) // 2capcity = min(pos, neg) # 取pos和neg中的较小者,以使得dp空间最小n = len(nums)# 初始化dp = [[0] * (capcity+1) for _ in range(n+1)]# dp[i][j]: 从前i个元素中选出若干个其和为j的方案数dp[0][0] = 1 # 其他 dp[0][j]均为0# 状态更新for i in range(1, n+1):for j in range(capcity+1):if j < nums[i-1]: # 容量有限,无法选择第i个数字nums[i-1]dp[i][j] = dp[i-1][j]else: # 可选择第i个数字nums[i-1],也可不选【两种方式之和】dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]]return dp[n][capcity]
2.3.2 第 N 个泰波那契数
1137. 第 N 个泰波那契数 - 力扣
给定一个整数 nnn,返回第 nnn 个泰波那契数。
- 泰波那契数:T0=0,T1=1,T2=1T_0 = 0, T_1 = 1, T_2 = 1T0=0,T1=1,T2=1,且在 n>=0n >= 0n>=0 的条件下,Tn+3=Tn+Tn+1+Tn+2T_{n + 3} = T_{n} + T_{n+1} + T_{n+2}Tn+3=Tn+Tn+1+Tn+2。
- 0≤n≤370 \le n \le 370≤n≤37。
- 答案保证是一个 32 位整数,即 answer≤231−1answer \le 2^{31} - 1answer≤231−1。
示例:
输入:n = 4
输出:4
解释:
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4
思路 1:记忆化搜索
- 问题的状态定义为:第 nnn 个泰波那契数。其状态转移方程为:T0=0,T1=1,T2=1T_0 = 0, T_1 = 1, T_2 = 1T0=0,T1=1,T2=1,且在 n>=0n >= 0n>=0 的条件下,Tn+3=Tn+Tn+1+Tn+2T_{n + 3} = T_{n} + T_{n+1} + T_{n+2}Tn+3=Tn+Tn+1+Tn+2。
- 定义一个长度为 n+1n + 1n+1 数组 memomemomemo 用于保存一斤个计算过的泰波那契数。
- 定义递归函数
my_tribonacci(n, memo)。- 当 n=0n = 0n=0 或者 n=1n = 1n=1,或者 n=2n = 2n=2 时直接返回结果。
- 当 n>2n > 2n>2 时,首先检查是否计算过 T(n)T(n)T(n),即判断 memo[n]memo[n]memo[n] 是否等于 000。
- 如果 memo[n]≠0memo[n] \ne 0memo[n]=0,说明已经计算过 T(n)T(n)T(n),直接返回 memo[n]memo[n]memo[n]。
- 如果 memo[n]=0memo[n] = 0memo[n]=0,说明没有计算过 T(n)T(n)T(n),则递归调用
my_tribonacci(n - 3, memo)、my_tribonacci(n - 2, memo)、my_tribonacci(n - 1, memo),并将计算结果存入 memo[n]memo[n]memo[n] 中,并返回 memo[n]memo[n]memo[n]。
class Solution:def tribonacci(self, n: int) -> int:# 使用数组保存已经求解过的 T(k) 的结果memo = [0 for _ in range(n + 1)]return self.my_tribonacci(n, memo)def my_tribonacci(self, n: int, memo: List[int]) -> int:if n == 0:return 0if n == 1 or n == 2:return 1if memo[n] != 0:return memo[n]memo[n] = self.my_tribonacci(n - 3, memo) + self.my_tribonacci(n - 2, memo) + self.my_tribonacci(n - 1, memo)return memo[n]
- 时间复杂度:O(n)O(n)O(n)。
- 空间复杂度:O(n)O(n)O(n)。
思路二:动态规划
class Solution(object):def tribonacci(self, n):""":type n: int:rtype: int"""if n<2:return nelif n==2:return 1dp=[0]*(n+1)dp[1]=1dp[2]=1for i in range(3,n+1):dp[i]=dp[i-1]+dp[i-2]+dp[i-3]return dp[n]
三、线性动态规划简介
参考:动态规划概念和基础线性DP | 潮汐朝夕
线性动态规划:具有「线性」阶段划分的动态规划方法统称为线性动态规划(简称为「线性 DP」),如下图所示。
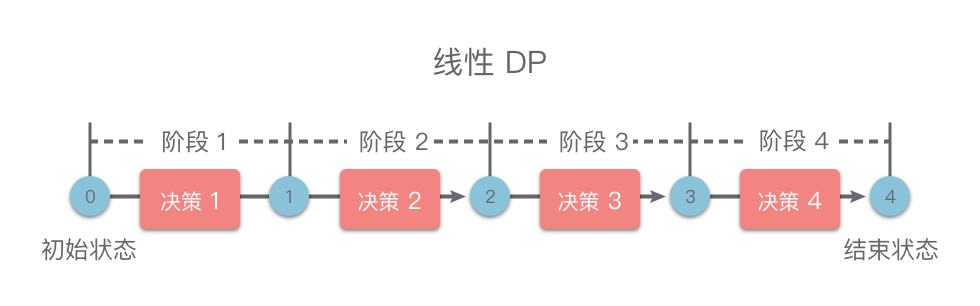
如果状态包含多个维度,但是每个维度上都是线性划分的阶段,也属于线性 DP。比如背包问题、区间 DP、数位 DP 等都属于线性 DP。
线性 DP 问题的划分方法有多种方式。
- 如果按照「状态的维度数」进行分类,我们可以将线性 DP 问题分为:一维线性 DP 问题、二维线性 DP 问题,以及多维线性 DP 问题。
- 如果按照「问题的输入格式」进行分类,我们可以将线性 DP 问题分为:单串线性 DP 问题、双串线性 DP 问题、矩阵线性 DP 问题,以及无串线性 DP 问题。
本文中,我们将按照问题的输入格式进行分类,对线性 DP 问题中各种类型问题进行一一讲解。
3.1 单串线性 DP 问题
3.1.1 最长递增子序列
300. 最长递增子序列 - 力扣
单串线性 DP 问题中最经典的问题就是「最长递增子序列(Longest Increasing Subsequence,简称 LIS)」。
给定一个整数数组 numsnumsnums,找到其中最长严格递增子序列的长度。
- 子序列:由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7][3,6,2,7][3,6,2,7] 是数组 [0,3,1,6,2,2,7][0,3,1,6,2,2,7][0,3,1,6,2,2,7] 的子序列。
- 1≤nums.length≤25001 \le nums.length \le 25001≤nums.length≤2500。
- −104≤nums[i]≤104-10^4 \le nums[i] \le 10^4−104≤nums[i]≤104。
示例:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4。
思路 1:动态规划
-
划分阶段
按照子序列的结尾位置进行阶段划分。 -
定义状态
定义状态 dp[i]dp[i]dp[i] 表示为:以 nums[i]nums[i]nums[i] 结尾的最长递增子序列长度。 -
状态转移方程
一个较小的数后边如果出现一个较大的数,则会形成一个更长的递增子序列。对于满足 0≤j<i0 \le j < i0≤j<i 的数组元素 nums[j]nums[j]nums[j] 和 nums[i]nums[i]nums[i] 来说:- 如果 nums[j]<nums[i]nums[j] < nums[i]nums[j]<nums[i],则 nums[i]nums[i]nums[i] 可以接在 nums[j]nums[j]nums[j] 后面,此时以 nums[i]nums[i]nums[i] 结尾的最长递增子序列长度会在「以 nums[j]nums[j]nums[j] 结尾的最长递增子序列长度」的基础上加 111,即:dp[i]=dp[j]+1dp[i] = dp[j] + 1dp[i]=dp[j]+1。
- 如果 nums[j]≤nums[i]nums[j] \le nums[i]nums[j]≤nums[i],则 nums[i]nums[i]nums[i] 不可以接在 nums[j]nums[j]nums[j] 后面,可以直接跳过。
综上,我们的状态转移方程为:dp[i]=max(dp[i],dp[j]+1),0≤j<i,nums[j]<nums[i]dp[i] = max(dp[i], dp[j] + 1),0 \le j < i,nums[j] < nums[i]dp[i]=max(dp[i],dp[j]+1),0≤j<i,nums[j]<nums[i]。
-
初始条件
默认状态下,把数组中的每个元素都作为长度为 111 的递增子序列。即 dp[i]=1dp[i] = 1dp[i]=1。 -
最终结果
根据我们之前定义的状态,dp[i]dp[i]dp[i] 表示为:以 nums[i]nums[i]nums[i] 结尾的最长递增子序列长度。那为了计算出最大的最长递增子序列长度,则需要再遍历一遍 dpdpdp 数组,求出最大值即为最终结果。
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:size = len(nums)dp = [1 for _ in range(size)]for i in range(size):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[i], dp[j] + 1)return max(dp) # 不是dp[n-1]
- 时间复杂度:O(n2)O(n^2)O(n2)。两重循环遍历的时间复杂度是 O(n2)O(n^2)O(n2),最后求最大值的时间复杂度是 O(n)O(n)O(n),所以总体时间复杂度为 O(n2)O(n^2)O(n2)。
- 空间复杂度:O(n)O(n)O(n)。用到了一维数组保存状态,所以总体空间复杂度为 O(n)O(n)O(n)。
3.1.2 最大子数组和
53. 最大子数组和 - 力扣
单串线性 DP 问题中除了子序列相关的线性 DP 问题,还有子数组相关的线性 DP 问题。
注意:
- 子序列:由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。
- 子数组:指的是数组中的一个连续子序列。
「子序列」与「子数组」都可以看做是原数组的一部分,而且都不会改变原来数组中元素的相对顺序。其区别在于数组元素是否要求连续。
给定一个整数数组 numsnumsnums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
- 子数组:指的是数组中的一个连续部分。
- 1≤nums.length≤1051 \le nums.length \le 10^51≤nums.length≤105。
- −104≤nums[i]≤104-10^4 \le nums[i] \le 10^4−104≤nums[i]≤104。
示例:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6。
3.1.2.1 动态规划
-
划分阶段
按照连续子数组的结束位置进行阶段划分。 -
定义状态
定义状态 dp[i]dp[i]dp[i] 为:以第 iii 个数结尾的连续子数组的最大和。 -
状态转移方程
状态 dp[i]dp[i]dp[i] 为:以第 iii 个数结尾的连续子数组的最大和。则我们可以从dp[i-1]来讨论dp[i]。- 如果
dp[i - 1] < 0,则dp[i - 1] + nums[i] < nums[i]。所以,此时dp[i]应取第 iii 个数的值,即dp[i] = nums[i]。 - 如果
dp[i - 1] ≥0,则dp[i] = dp[i - 1] + nums[i]。
- 如果
归纳一下,状态转移方程为:
dp[i]={nums[i],dp[i−1]<0dp[i−1]+nums[i]dp[i−1]≥0dp[i] = \begin{cases} nums[i], & dp[i - 1] < 0 \cr dp[i - 1] + nums[i] & dp[i - 1] \ge 0 \end{cases}dp[i]={nums[i],dp[i−1]+nums[i]dp[i−1]<0dp[i−1]≥0
-
初始条件
第 000 个数结尾的连续子数组的最大和为 nums[0]nums[0]nums[0],即 dp[0]=nums[0]dp[0] = nums[0]dp[0]=nums[0]。 -
最终结果
根据状态定义,dp[i]dp[i]dp[i] 为:以第 iii 个数结尾的连续子数组的最大和。则最终结果应为所有 dp[i]dp[i]dp[i] 的最大值,即 max(dp)max(dp)max(dp)。
class Solution:def maxSubArray(self, nums: List[int]) -> int:size = len(nums)dp = [0 for _ in range(size)]dp[0] = nums[0]for i in range(1, size):if dp[i - 1] < 0:dp[i] = nums[i]else:dp[i] = dp[i - 1] + nums[i]return max(dp)
- 时间复杂度:O(n)O(n)O(n),其中 nnn 为数组 numsnumsnums 的元素个数。
- 空间复杂度:O(n)O(n)O(n)。
3.1.2.2 动态规划+滚动数组
因为 dp[i]dp[i]dp[i] 只和 dp[i−1]dp[i - 1]dp[i−1] 和当前元素 nums[i]nums[i]nums[i] 相关,我们也可以使用一个变量 subMaxsubMaxsubMax 来表示以第 iii 个数结尾的连续子数组的最大和。然后使用 ansMaxansMaxansMax 来保存全局中最大值。
class Solution:def maxSubArray(self, nums: List[int]) -> int:size = len(nums)subMax = nums[0]ansMax = nums[0]for i in range(1, size):if subMax < 0:subMax = nums[i]else:subMax += nums[i]ansMax = max(ansMax, subMax)return ansMax
- 时间复杂度:O(n)O(n)O(n),其中 nnn 为数组 numsnumsnums 的元素个数。
- 空间复杂度:O(1)O(1)O(1)。
3.1.3 最长的斐波那契子序列的长度
有一些单串线性 DP 问题在定义状态时需要考虑两个结束位置,只考虑一个结束位置的无法清楚描述问题。这时候我们就需要需要增加一个结束位置维度来定义状态。
873. 最长的斐波那契子序列的长度 - 力扣
给定一个严格递增的正整数数组 arrarrarr,要求从数组 arrarrarr 中找出最长的斐波那契式的子序列的长度。如果不存斐波那契式的子序列,则返回 0。
-
斐波那契式序列:如果序列 X1,X2,...,XnX_1, X_2, ..., X_nX1,X2,...,Xn 满足
- n≥3n \ge 3n≥3;
- 对于所有 i+2≤ni + 2 \le ni+2≤n,都有 Xi+Xi+1=Xi+2X_i + X_{i+1} = X_{i+2}Xi+Xi+1=Xi+2,则称该序列为斐波那契式序列。
-
斐波那契式子序列:从序列 AAA 中挑选若干元素组成子序列,并且子序列满足斐波那契式序列,则称该序列为斐波那契式子序列。例如:A=[3,4,5,6,7,8]A = [3, 4, 5, 6, 7, 8]A=[3,4,5,6,7,8]。则 [3,5,8][3, 5, 8][3,5,8] 是 AAA 的一个斐波那契式子序列。
-
3≤arr.length≤10003 \le arr.length \le 10003≤arr.length≤1000。
-
1≤arr[i]<arr[i+1]≤1091 \le arr[i] < arr[i + 1] \le 10^91≤arr[i]<arr[i+1]≤109。
示例:
输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18]。
3.1.3.1 暴力枚举(超时)
假设 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j]、arr[k]arr[k]arr[k] 是序列 arrarrarr 中的 333 个元素,且满足关系:arr[i]+arr[j]==arr[k]arr[i] + arr[j] == arr[k]arr[i]+arr[j]==arr[k],则 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j]、arr[k]arr[k]arr[k] 就构成了 arrarrarr 的一个斐波那契式子序列。
通过 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j],我们可以确定下一个斐波那契式子序列元素的值为 arr[i]+arr[j]arr[i] + arr[j]arr[i]+arr[j]。
因为给定的数组是严格递增的,所以对于一个斐波那契式子序列,如果确定了 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j],则可以顺着 arrarrarr 序列,从第 j+1j + 1j+1 的元素开始,查找值为 arr[i]+arr[j]arr[i] + arr[j]arr[i]+arr[j] 的元素 。找到 arr[i]+arr[j]arr[i] + arr[j]arr[i]+arr[j] 之后,然后再顺着查找子序列的下一个元素。
简单来说,就是确定了 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j],就能尽可能的得到一个长的斐波那契式子序列,此时我们记录下子序列长度。然后对于不同的 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j],统计不同的斐波那契式子序列的长度。
最后将这些长度进行比较,其中最长的长度就是答案。
class Solution:def lenLongestFibSubseq(self, arr: List[int]) -> int:size = len(arr)ans = 0for i in range(size):for j in range(i + 1, size):temp_ans = 0temp_i = itemp_j = jk = j + 1while k < size:if arr[temp_i] + arr[temp_j] == arr[k]:temp_ans += 1temp_i = temp_jtemp_j = kk += 1if temp_ans > ans:ans = temp_ansif ans > 0:return ans + 2else:return ans
- 时间复杂度:O(n3)O(n^3)O(n3),其中 nnn 为数组 arrarrarr 的元素个数。
- 空间复杂度:O(1)O(1)O(1)。
3.1.3.2 哈希表
对于 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j],要查找的元素 arr[i]+arr[j]arr[i] + arr[j]arr[i]+arr[j] 是否在 arrarrarr 中,我们可以预先建立一个反向的哈希表。键值对关系为 value:idxvalue : idxvalue:idx,这样就能在 O(1)O(1)O(1) 的时间复杂度通过 arr[i]+arr[j]arr[i] + arr[j]arr[i]+arr[j] 的值查找到对应的 arr[k]arr[k]arr[k],而不用像原先一样线性查找 arr[k]arr[k]arr[k] 了。
class Solution:def lenLongestFibSubseq(self, arr: List[int]) -> int:size = len(arr)ans = 0idx_map = dict()for idx, value in enumerate(arr):idx_map[value] = idxfor i in range(size):for j in range(i + 1, size):temp_ans = 0temp_i = itemp_j = jwhile arr[temp_i] + arr[temp_j] in idx_map:temp_ans += 1k = idx_map[arr[temp_i] + arr[temp_j]]temp_i = temp_jtemp_j = kif temp_ans > ans:ans = temp_ansif ans > 0:return ans + 2else:return ans
- 时间复杂度:O(n2)O(n^2)O(n2),其中 nnn 为数组 arrarrarr 的元素个数。
- 空间复杂度:O(n)O(n)O(n)。
3.1.3.3 动态规划 + 哈希表
-
划分阶段
按照斐波那契式子序列相邻两项的结尾位置进行阶段划分。 -
定义状态
定义状态 dp[i][j]dp[i][j]dp[i][j] 表示为:以 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j] 为结尾的斐波那契式子序列的最大长度。 -
状态转移方程
如果arr[i]+arr[j]=arr[k]arr[i] + arr[j] = arr[k]arr[i]+arr[j]=arr[k] ,则以 arr[i]arr[i]arr[i]、arr[k]arr[k]arr[k] 结尾的斐波那契式子序列的最大长度,等于以 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j] 为结尾的斐波那契式子序列的最大长度加 111。即状态转移方程为:dp[j][k]=max(A[i]+A[j]=A[k],i<j<k)(dp[i][j]+1)dp[j][k] = max_{(A[i] + A[j] = A[k],i < j < k)}(dp[i][j] + 1)dp[j][k]=max(A[i]+A[j]=A[k],i<j<k)(dp[i][j]+1)。 -
初始条件
默认状态下,数组中任意相邻两项元素都可以作为长度为 222 的斐波那契式子序列,即 dp[i][j]=2dp[i][j] = 2dp[i][j]=2。 -
最终结果
根据我们之前定义的状态,dp[i][j]dp[i][j]dp[i][j] 表示为:以 arr[i]arr[i]arr[i]、arr[j]arr[j]arr[j] 为结尾的斐波那契式子序列的最大长度。那为了计算出最大的最长递增子序列长度,则需要在进行状态转移时,求出最大值 ansansans 即为最终结果。
因为题目定义中,斐波那契式中 n≥3n \ge 3n≥3,所以只有当 ans≥3ans \ge 3ans≥3 时,返回 ansansans。如果 ans<3ans < 3ans<3,则返回 000。
注意:在进行状态转移的同时,我们应和「思路 2:哈希表」一样采用哈希表优化的方式来提高效率,降低算法的时间复杂度。
class Solution:def lenLongestFibSubseq(self, arr: List[int]) -> int:size = len(arr)if size<3:return 0dp = [[0 for _ in range(size)] for _ in range(size)]ans = 0# 初始化 dpfor i in range(size):for j in range(i + 1, size):dp[i][j] = 2d = {}# 将 value : idx 映射为哈希表,这样可以快速通过 value 获取到 idxfor idx, value in enumerate(arr):d[value] = idxfor i in range(size):for j in range(i + 1, size):if arr[i] + arr[j] in idx_map: # 获取 arr[i] + arr[j] 的 idx,即斐波那契式子序列下一项元素k = d[arr[i] + arr[j]]dp[j][k] = max(dp[j][k], dp[i][j] + 1)ans = max(ans, dp[j][k])return ans
- 时间复杂度:O(n2)O(n^2)O(n2),其中 nnn 为数组 arrarrarr 的元素个数。
- 空间复杂度:O(n)O(n)O(n)。
3.2 双串线性 DP 问题
双串线性 DP 问题:问题的输入为两个数组或两个字符串的线性 DP 问题。状态一般可定义为 dp[i][j]dp[i][j]dp[i][j],表示为:
- 「以第一个数组中第 iii 个位置元素 nums1[i]nums1[i]nums1[i] 为结尾的子数组(nums1[0]...nums1[i]nums1[0]...nums1[i]nums1[0]...nums1[i])」与「以第二个数组中第 jjj 个位置元素 nums2[j]nums2[j]nums2[j] 为结尾的子数组(nums2[0]...nums2[j]nums2[0]...nums2[j]nums2[0]...nums2[j])」的相关解。
- 「以第一个数组中第 i−1i - 1i−1 个位置元素 nums1[i−1]nums1[i - 1]nums1[i−1] 为结尾的子数组(nums1[0]...nums1[i−1]nums1[0]...nums1[i - 1]nums1[0]...nums1[i−1])」与「以第二个数组中第 j−1j - 1j−1 个位置元素 nums2[j−1]nums2[j - 1]nums2[j−1] 为结尾的子数组(nums2[0]...nums2[j−1]nums2[0]...nums2[j - 1]nums2[0]...nums2[j−1])」的相关解。
- 「以第一个数组中前 iii 个元素为子数组(nums1[0]...nums1[i−1]nums1[0]...nums1[i - 1]nums1[0]...nums1[i−1])」与「以第二个数组中前 jjj 个元素为子数组(nums2[0]...nums2[j−1]nums2[0]...nums2[j - 1]nums2[0]...nums2[j−1])」的相关解。
这 333 种状态的定义区别在于相差一个元素 nums1[i]nums1[i]nums1[i] 或 nums2[j]nums2[j]nums2[j]。
- 第 111 种状态:子数组的长度为 i+1i + 1i+1 或 j+1j + 1j+1,子数组长度可为空
- 第 222 种状态、第 333 种状态:子数组的长度为 iii 或 jjj,子数组长度不可为空。
双串线性 DP 问题中最经典的问题就是「最长公共子序列(Longest Common Subsequence,简称 LCS)」。
3.2.1 最长公共子序列
1143. 最长公共子序列 - 力扣
给定两个字符串 text1text1text1 和 text2text2text2,要求返回两个字符串的最长公共子序列的长度。如果不存在公共子序列,则返回 000。
- 子序列:原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 公共子序列:两个字符串所共同拥有的子序列。
- 1≤text1.length,text2.length≤10001 \le text1.length, text2.length \le 10001≤text1.length,text2.length≤1000。
- text1text1text1 和 text2text2text2 仅由小写英文字符组成。
示例:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
思路 1:动态规划
-
划分阶段
按照两个字符串的结尾位置进行阶段划分。 -
定义状态
定义状态 dp[i][j]dp[i][j]dp[i][j] 表示为:「以 text1text1text1 中前 iii 个元素组成的子字符串 str1str1str1 」与「以 text2text2text2 中前 jjj 个元素组成的子字符串 str2str2str2」的最长公共子序列长度为 dp[i][j]dp[i][j]dp[i][j]。 -
状态转移方程
双重循环遍历字符串 text1text1text1 和 text2text2text2,则状态转移方程为:- 如果 text1[i−1]=text2[j−1]text1[i - 1] = text2[j - 1]text1[i−1]=text2[j−1],说明两个子字符串的最后一位是相同的,所以最长公共子序列长度加 111。即:dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j]=dp[i−1][j−1]+1。
- 如果 text1[i−1]≠text2[j−1]text1[i - 1] \ne text2[j - 1]text1[i−1]=text2[j−1],说明两个子字符串的最后一位是不同的,则 dp[i][j]dp[i][j]dp[i][j] 需要考虑以下两种情况,取两种情况中最大的那种:dp[i][j]=max(dp[i−1][j],dp[i][j−1])dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])dp[i][j]=max(dp[i−1][j],dp[i][j−1])。
- str1[0:i−1]str1[0:i-1]str1[0:i−1]与str2[j]str2[j]str2[j]的最长公共子序列长度,即 dp[i−1][j]dp[i - 1][j]dp[i−1][j]。
- str1[0:i]str1[0:i]str1[0:i]与str2[j−1]str2[j-1]str2[j−1]的最长公共子序列长度,即 dp[i][j−1]dp[i][j - 1]dp[i][j−1]。
-
初始条件
- 当 i=0i = 0i=0 时,str1str1str1 表示的是空串,空串与 str2str2str2 的最长公共子序列长度为 000,即 dp[0][j]=0dp[0][j] = 0dp[0][j]=0。
- 当 j=0j = 0j=0 时,str2str2str2 表示的是空串,str1str1str1 与 空串的最长公共子序列长度为 000,即 dp[i][0]=0dp[i][0] = 0dp[i][0]=0。
-
最终结果
根据状态定义,最后输出 dp[sise1][size2]dp[sise1][size2]dp[sise1][size2](即 text1text1text1 与 text2text2text2 的最长公共子序列长度)即可,其中 size1size1size1、size2size2size2 分别为 text1text1text1、text2text2text2 的字符串长度。
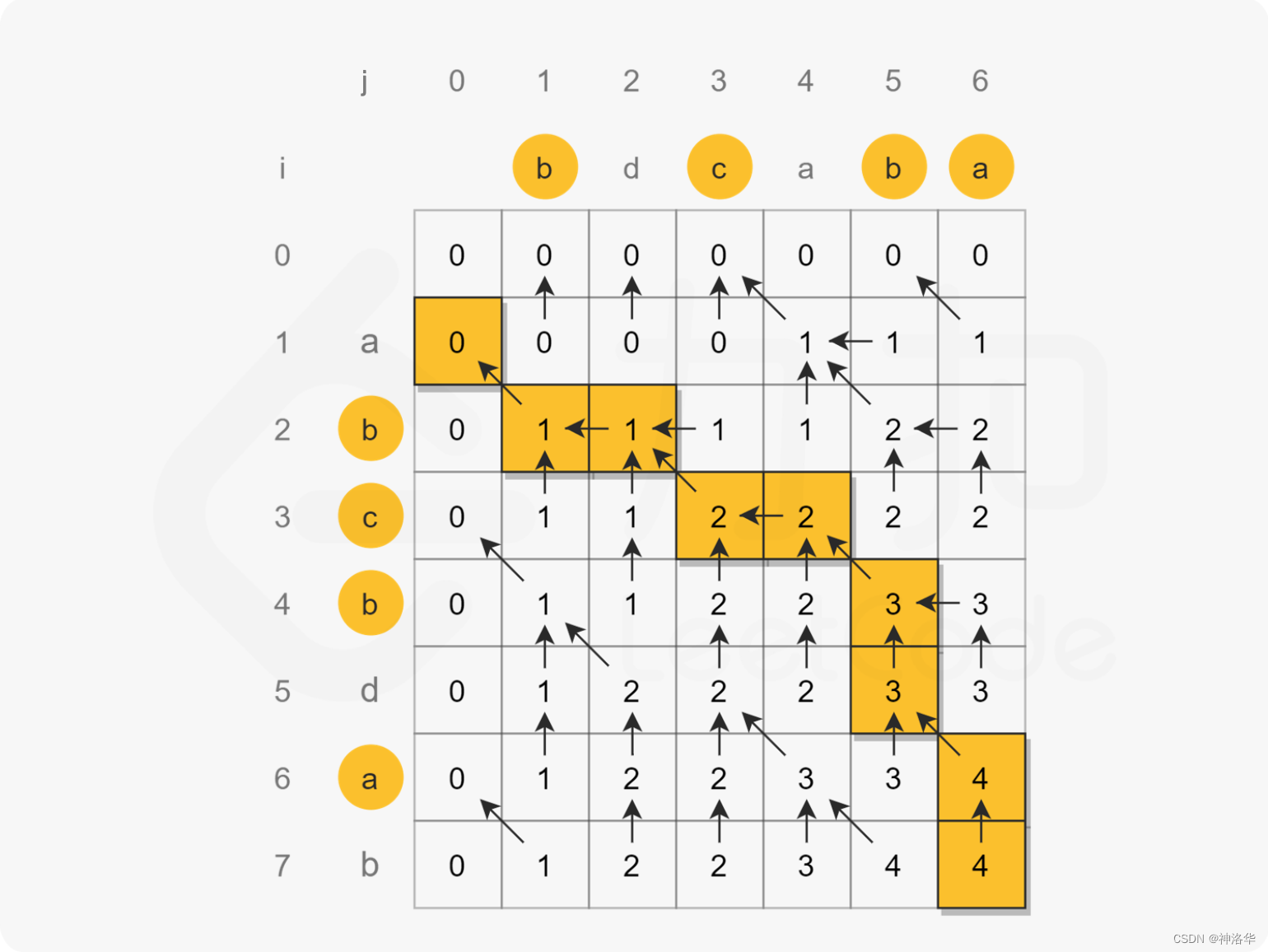
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:size1 = len(text1)size2 = len(text2)dp = [[0 for _ in range(size2 + 1)] for _ in range(size1 + 1)]for i in range(1, size1 + 1):for j in range(1, size2 + 1):if text1[i - 1] == text2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[size1][size2]
- 时间复杂度:O(n×m)O(n \times m)O(n×m),其中 nnn、mmm 分别是字符串 text1text1text1、text2text2text2 的长度。两重循环遍历的时间复杂度是 O(n×m)O(n \times m)O(n×m),所以总的时间复杂度为 O(n×m)O(n \times m)O(n×m)。
- 空间复杂度:O(n×m)O(n \times m)O(n×m)。用到了二维数组保存状态,所以总体空间复杂度为 O(n×m)O(n \times m)O(n×m)。
3.2.2 最长重复子数组
718. 最长重复子数组 - 力扣
给定两个整数数组 nums1nums1nums1、nums2nums2nums2,计算两个数组中公共的、长度最长的子数组长度。
- 1≤nums1.length,nums2.length≤10001 \le nums1.length, nums2.length \le 10001≤nums1.length,nums2.length≤1000。
- 0≤nums1[i],nums2[i]≤1000 \le nums1[i], nums2[i] \le 1000≤nums1[i],nums2[i]≤100。
示例:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
思路 1:动态规划
-
划分阶段
按照子数组结尾位置进行阶段划分。 -
定义状态
定义状态 dp[i][j]dp[i][j]dp[i][j] 为:「以 nums1nums1nums1 中前 iii 个元素为子数组(nums1[0]...nums2[i−1]nums1[0]...nums2[i - 1]nums1[0]...nums2[i−1])」和「以 nums2nums2nums2 中前 jjj 个元素为子数组(nums2[0]...nums2[j−1]nums2[0]...nums2[j - 1]nums2[0]...nums2[j−1])」的最长公共子数组长度。 -
状态转移方程
- 如果 nums1[i−1]=nums2[j−1]nums1[i - 1] = nums2[j - 1]nums1[i−1]=nums2[j−1],则当前元素可以构成公共子数组,此时 dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j]=dp[i−1][j−1]+1。
- 如果 nums1[i−1]≠nums2[j−1]nums1[i - 1] \ne nums2[j - 1]nums1[i−1]=nums2[j−1],则当前元素不能构成公共子数组,此时 dp[i][j]=0dp[i][j] = 0dp[i][j]=0。
-
初始条件
- 当 i=0i = 0i=0 时,nums1[0]...nums1[i−1]nums1[0]...nums1[i - 1]nums1[0]...nums1[i−1] 表示的是空数组,空数组与 nums2[0]...nums2[j−1]nums2[0]...nums2[j - 1]nums2[0]...nums2[j−1] 的最长公共子序列长度为 000,即 dp[0][j]=0dp[0][j] = 0dp[0][j]=0。
- 当 j=0j = 0j=0 时,nums2[0]...nums2[j−1]nums2[0]...nums2[j - 1]nums2[0]...nums2[j−1] 表示的是空数组,空数组与 nums1[0]...nums1[i−1]nums1[0]...nums1[i - 1]nums1[0]...nums1[i−1] 的最长公共子序列长度为 000,即 dp[i][0]=0dp[i][0] = 0dp[i][0]=0。
-
最终结果
根据状态定义, dp[i][j]dp[i][j]dp[i][j] 为:「以 nums1nums1nums1 中前 iii 个元素为子数组(nums1[0]...nums2[i−1]nums1[0]...nums2[i - 1]nums1[0]...nums2[i−1])」和「以 nums2nums2nums2 中前 jjj 个元素为子数组(nums2[0]...nums2[j−1]nums2[0]...nums2[j - 1]nums2[0]...nums2[j−1])」的最长公共子数组长度。在遍历过程中,我们可以使用 resresres 记录下所有 dp[i][j]dp[i][j]dp[i][j] 中最大值即为答案。
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:size1 = len(nums1)size2 = len(nums2)dp = [[0 for _ in range(size2 + 1)] for _ in range(size1 + 1)]res = 0for i in range(1, size1 + 1):for j in range(1, size2 + 1):if nums1[i - 1] == nums2[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1if dp[i][j] > res:res = dp[i][j]return res
- 时间复杂度:O(n×m)O(n \times m)O(n×m)。其中 nnn 是数组 nums1nums1nums1 的长度,mmm 是数组 nums2nums2nums2 的长度。
- 空间复杂度:O(n×m)O(n \times m)O(n×m)。
3.3.3 编辑距离
双串线性 DP 问题中除了经典的最长公共子序列问题之外,还包括字符串的模糊匹配问题。
72. 编辑距离 - 力扣
给定两个单词 word1word1word1、word2word2word2。对一个单词可以进行以下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
请计算出将 word1word1word1 转换为 word2word2word2 所使用的最少操作数。
- 0≤word1.length,word2.length≤5000 \le word1.length, word2.length \le 5000≤word1.length,word2.length≤500。
- word1word1word1 和 word2word2word2 由小写英文字母组成。
示例:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
思路 1:动态规划
-
划分阶段
按照两个字符串的结尾位置进行阶段划分。 -
定义状态
定义状态 dp[i][j]dp[i][j]dp[i][j] 表示为:「以 word1word1word1 中前 iii 个字符组成的子字符串 str1str1str1」变为「以 word2word2word2 中前 jjj 个字符组成的子字符串 str2str2str2」,所需要的最少操作次数。 -
状态转移方程
- 如果当前字符相同(word1[i−1]=word2[j−1]word1[i - 1] = word2[j - 1]word1[i−1]=word2[j−1]),无需插入、删除、替换。dp[i][j]=dp[i−1][j−1]dp[i][j] = dp[i - 1][j - 1]dp[i][j]=dp[i−1][j−1]。
- 如果当前字符不同(word1[i−1]≠word2[j−1]word1[i - 1] \ne word2[j - 1]word1[i−1]=word2[j−1]),dp[i][j]dp[i][j]dp[i][j] 取源于以下三种情况中的最小情况:
- 替换(word1[i−1]word1[i - 1]word1[i−1] 替换为 word2[j−1]word2[j - 1]word2[j−1]):最少操作次数依赖于「以 word1word1word1 中前 i−1i - 1i−1 个字符组成的子字符串 str1str1str1」变为「以 word2word2word2 中前 j−1j - 1j−1 个字符组成的子字符串 str2str2str2」,再加上替换的操作数 111,即:dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j]=dp[i−1][j−1]+1。
- 插入(word1word1word1 在第 i−1i - 1i−1 位置上插入元素):最少操作次数依赖于「以 word1word1word1 中前 i−1i - 1i−1 个字符组成的子字符串 str1str1str1」 变为「以 word2word2word2 中前 jjj 个字符组成的子字符串 str2str2str2」,再加上插入需要的操作数 111,即:dp[i][j]=dp[i−1][j]+1dp[i][j] = dp[i - 1][j] + 1dp[i][j]=dp[i−1][j]+1。
- 删除(word1word1word1 删除第 i−1i - 1i−1 位置元素):最少操作次数依赖于「以 word1word1word1 中前 iii 个字符组成的子字符串 str1str1str1」变为「以 word2word2word2 中前 j−1j - 1j−1 个字符组成的子字符串 str2str2str2」,再加上删除需要的操作数 111,即:dp[i][j]=dp[i][j−1]+1dp[i][j] = dp[i][j - 1] + 1dp[i][j]=dp[i][j−1]+1。
综合上述情况,状态转移方程为:
dp[i][j]={dp[i−1][j−1]word1[i−1]=word2[j−1]min(dp[i−1][j−1],dp[i−1][j],dp[i][j−1])+1word1[i−1]≠word2[j−1]dp[i][j] = \begin{cases} dp[i - 1][j - 1] & word1[i - 1] = word2[j - 1] \cr min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1 & word1[i - 1] \ne word2[j - 1] \end{cases}dp[i][j]={dp[i−1][j−1]min(dp[i−1][j−1],dp[i−1][j],dp[i][j−1])+1word1[i−1]=word2[j−1]word1[i−1]=word2[j−1]
-
初始条件
- 当 i=0i = 0i=0, str1str1str1为空字符串,str1str1str1变为str2str2str2时,至少需要插入 jjj 次,即:dp[0][j]=jdp[0][j] = jdp[0][j]=j。
- 当 j=0j = 0j=0,str2str2str2为空字符串, str1str1str1变为str2str2str2时,至少需要删除 iii 次,即:dp[i][0]=idp[i][0] = idp[i][0]=i。
-
最终结果
根据状态定义,最后输出 dp[sise1][size2]dp[sise1][size2]dp[sise1][size2](即 word1word1word1 变为 word2word2word2 所使用的最少操作数)即可。其中 size1size1size1、size2size2size2 分别为 word1word1word1、word2word2word2 的字符串长度。
class Solution:def minDistance(self, word1: str, word2: str) -> int:size1 = len(word1)size2 = len(word2)dp = [[0 for _ in range(size2 + 1)] for _ in range(size1 + 1)]for i in range(size1 + 1):dp[i][0] = ifor j in range(size2 + 1):dp[0][j] = jfor i in range(1, size1 + 1):for j in range(1, size2 + 1):if word1[i - 1] == word2[j - 1]:dp[i][j] = dp[i - 1][j - 1]else:dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1return dp[size1][size2]
- 时间复杂度:O(n×m)O(n \times m)O(n×m),其中 nnn、mmm 分别是字符串 word1word1word1、word2word2word2 的长度。两重循环遍历的时间复杂度是 O(n×m)O(n \times m)O(n×m),所以总的时间复杂度为 O(n×m)O(n \times m)O(n×m)。
- 空间复杂度:O(n×m)O(n \times m)O(n×m)。用到了二维数组保存状态,所以总体空间复杂度为 O(n×m)O(n \times m)O(n×m)。
3.3 矩阵线性 DP问题
矩阵线性 DP 问题:问题的输入为二维矩阵的线性 DP 问题。状态一般可定义为 dp[i][j]dp[i][j]dp[i][j],表示为:从「位置 (0,0)(0, 0)(0,0)」到达「位置 (i,j)(i, j)(i,j)」的相关解。
3.3.1 最小路径和
64. 最小路径和 - 力扣
给定一个包含非负整数的 m×nm \times nm×n 大小的网格 gridgridgrid,找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
- 每次只能向下或者向右移动一步。
- m==grid.lengthm == grid.lengthm==grid.length。
- n==grid[i].lengthn == grid[i].lengthn==grid[i].length。
- 1≤m,n≤2001 \le m, n \le 2001≤m,n≤200。
- 0≤grid[i][j]≤1000 \le grid[i][j] \le 1000≤grid[i][j]≤100。
示例:
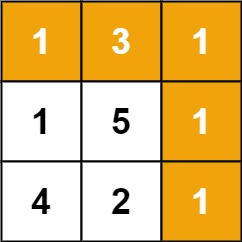
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
思路 1:动态规划
-
划分阶段
按照路径的结尾位置(行位置、列位置组成的二维坐标)进行阶段划分。 -
定义状态
定义状态 dp[i][j]dp[i][j]dp[i][j] 为:从位置 (0,0)(0, 0)(0,0) 到达位置 (i,j)(i, j)(i,j) 的最小路径和。 -
状态转移方程
当前位置 (i,j)(i, j)(i,j) 只能从左侧位置 (i,j−1)(i, j - 1)(i,j−1) 或者上方位置 (i−1,j)(i - 1, j)(i−1,j) 到达。为了使得从左上角到达 (i,j)(i, j)(i,j) 位置的最小路径和最小,应从 (i,j−1)(i, j - 1)(i,j−1) 位置和 (i−1,j)(i - 1, j)(i−1,j) 位置选择路径和最小的位置达到 (i,j)(i, j)(i,j)。即状态转移方程为:dp[i][j]=min(dp[i][j−1],dp[i−1][j])+grid[i][j]dp[i][j] = min(dp[i][j - 1], dp[i - 1][j]) + grid[i][j]dp[i][j]=min(dp[i][j−1],dp[i−1][j])+grid[i][j] -
初始条件
- 当左侧和上方是矩阵边界时(即 i=0,j=0i = 0, j = 0i=0,j=0),dp[i][j]=grid[i][j]dp[i][j] = grid[i][j]dp[i][j]=grid[i][j]。
- 当只有左侧是矩阵边界时(即 i≠0,j=0i \ne 0, j = 0i=0,j=0),只能从上方到达,dp[i][j]=dp[i−1][j]+grid[i][j]dp[i][j] = dp[i - 1][j] + grid[i][j]dp[i][j]=dp[i−1][j]+grid[i][j]。
- 当只有上方是矩阵边界时(即 i=0,j≠0i = 0, j \ne 0i=0,j=0),只能从左侧到达,dp[i][j]=dp[i][j−1]+grid[i][j]dp[i][j] = dp[i][j - 1] + grid[i][j]dp[i][j]=dp[i][j−1]+grid[i][j]。
-
最终结果
根据状态定义,最后输出 dp[rows−1][cols−1]dp[rows - 1][cols - 1]dp[rows−1][cols−1](即从左上角到达 (rows−1,cols−1)(rows - 1, cols - 1)(rows−1,cols−1) 位置的最小路径和)即可。其中 rowsrowsrows、colscolscols 分别为 gridgridgrid 的行数、列数。
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:rows, cols = len(grid), len(grid[0])dp = [[0 for _ in range(cols)] for _ in range(rows)]dp[0][0] = grid[0][0]for i in range(1, rows):dp[i][0] = dp[i - 1][0] + grid[i][0]for j in range(1, cols):dp[0][j] = dp[0][j - 1] + grid[0][j]for i in range(1, rows):for j in range(1, cols):dp[i][j] = min(dp[i][j - 1], dp[i - 1][j]) + grid[i][j]return dp[rows - 1][cols - 1]
- 时间复杂度:O(m∗n)O(m * n)O(m∗n),其中 mmm、nnn 分别为 gridgridgrid 的行数和列数。
- 空间复杂度:O(m∗n)O(m * n)O(m∗n)。
3.3.2最大正方形
221. 最大正方形 - 力扣
给定一个由 '0' 和 '1' 组成的二维矩阵 matrixmatrixmatrix,找到只包含 '1' 的最大正方形,并返回其面积。
- m==matrix.lengthm == matrix.lengthm==matrix.length。
- n==matrix[i].lengthn == matrix[i].lengthn==matrix[i].length。
- 1≤m,n≤3001 \le m, n \le 3001≤m,n≤300。
- matrix[i][j]matrix[i][j]matrix[i][j] 为
'0'或'1'。
示例:
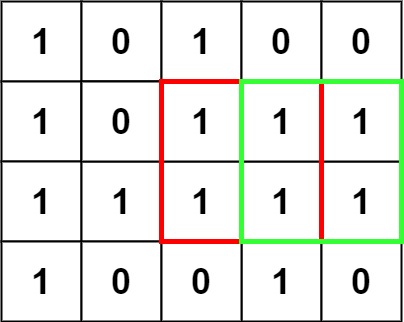
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
思路 1:动态规划
-
划分阶段
按照正方形的右下角坐标进行阶段划分。 -
定义状态
定义状态 dp[i][j]dp[i][j]dp[i][j] 表示为:以矩阵位置 (i,j)(i, j)(i,j) 为右下角,且值包含 111 的正方形的最大边长。 -
状态转移方程
只有当矩阵位置 (i,j)(i, j)(i,j) 值为 111 时,才有可能存在正方形。- 如果矩阵位置 (i,j)(i, j)(i,j) 上值为 000,则 dp[i][j]=0dp[i][j] = 0dp[i][j]=0。
- 如果矩阵位置 (i,j)(i, j)(i,j) 上值为 111,则 dp[i][j]dp[i][j]dp[i][j] 的值由该位置上方、左侧、左上方三者共同约束的,为三者中最小值加 111。即:dp[i][j]=min(dp[i−1][j−1],dp[i−1][j],dp[i][j−1])+1dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1dp[i][j]=min(dp[i−1][j−1],dp[i−1][j],dp[i][j−1])+1。
-
初始条件
默认所有以矩阵位置 (i,j)(i, j)(i,j) 为右下角,且值包含 111 的正方形的最大边长都为 000,即 dp[i][j]=0dp[i][j] = 0dp[i][j]=0。 -
最终结果
根据我们之前定义的状态, dp[i][j]dp[i][j]dp[i][j] 表示为:以矩阵位置 (i,j)(i, j)(i,j) 为右下角,且值包含 111 的正方形的最大边长。则最终结果为所有 dp[i][j]dp[i][j]dp[i][j] 中的最大值。
class Solution:def maximalSquare(self, matrix: List[List[str]]) -> int:rows, cols = len(matrix), len(matrix[0])max_size = 0dp = [[0 for _ in range(cols)] for _ in range(rows)]for i in range(rows):for j in range(cols):if matrix[i][j] == '1':# 第一行或第一列某个位置为“1”,则其dp值为1,因为是最小正方形if i == 0 or j == 0:dp[i][j] = 1# 其它位置为“1”时,只有左侧、上方和左上方三个位置都是“1”,这个位置值才+1else:dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1max_size = max(max_size, dp[i][j])return max_size * max_size
- 时间复杂度:O(m×n)O(m \times n)O(m×n),其中 mmm、nnn 分别为二维矩阵 matrixmatrixmatrix 的行数和列数。
- 空间复杂度:O(m×n)O(m \times n)O(m×n)。
3.4无串线性 DP 问题
无串线性 DP 问题:问题的输入不是显式的数组或字符串,但依然可分解为若干子问题的线性 DP 问题。
3.4.1 整数拆分
343. 整数拆分 - 力扣
给定一个正整数 nnn,将其拆分为 k(k≥2)k (k \ge 2)k(k≥2) 个正整数的和,并使这些整数的乘积最大化,返回可以获得的最大乘积。
- 2≤n≤582 \le n \le 582≤n≤58。
示例:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
思路 1:动态规划
-
划分阶段
按照正整数进行划分。 -
定义状态
定义状态 dp[i]dp[i]dp[i] 表示为:将正整数 iii 拆分为至少 222 个正整数的和之后,这些正整数的最大乘积。 -
状态转移方程
始终要记得自己定义的dp数组的含义
当 i≥2i \ge 2i≥2 时,假设正整数 iii 拆分出的第 111 个正整数是 j(1≤j<i)j(1 \le j < i)j(1≤j<i),则有两种方法:- 将 iii 拆分为 jjj 和 i−ji - ji−j 的和,且 i−ji - ji−j 不再拆分为多个正整数,此时乘积为:j×(i−j)j \times (i - j)j×(i−j)。
- 将 iii 拆分为 jjj 和 i−ji - ji−j 的和,且 i−ji - ji−j 继续拆分为多个正整数,此时乘积为:j×dp[i−j]j \times dp[i - j]j×dp[i−j]。
则 dp[i]dp[i]dp[i] 取两者中的最大值。即:dp[i]=max(j×(i−j),j×dp[i−j])dp[i] = max(j \times (i - j), j \times dp[i - j])dp[i]=max(j×(i−j),j×dp[i−j])。
由于 1≤j<i1 \le j < i1≤j<i,需要遍历 jjj 得到 dp[i]dp[i]dp[i] 的最大值,则状态转移方程如下:
dp[i]=max1≤j<i{max(j×(i−j),j×dp[i−j])}dp[i] = max_{1 \le j < i}\lbrace max(j \times (i - j), j \times dp[i - j]) \rbracedp[i]=max1≤j<i{max(j×(i−j),j×dp[i−j])}
-
初始条件
000 和 111 都不能被拆分,所以 dp[0]=0,dp[1]=0dp[0] = 0, dp[1] = 0dp[0]=0,dp[1]=0。 -
最终结果
根据我们之前定义的状态,dp[i]dp[i]dp[i] 表示为:将正整数 iii 拆分为至少 222 个正整数的和之后,这些正整数的最大乘积。则最终结果为 dp[n]dp[n]dp[n]。
class Solution:def integerBreak(self, n: int) -> int:dp = [0 for _ in range(n + 1)]for i in range(2, n + 1):for j in range(i):dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)return dp[n]
- 时间复杂度:O(n2)O(n^2)O(n2)。
- 空间复杂度:O(n)O(n)O(n)。
思路 2:动态规划优化
思路1中计算dp[i] 时,j 的值遍历了从 1 到 i−1 的所有值,因此总时间复杂度是O(n2)O(n^2)O(n2)。继续分析可知,要想得到最大乘积,j只能取2或者3(详见《官方题解》),则状态转移方程为:
dp[i]=max(2×(i−2),2×dp[i−2],3×(i−3),3×dp[i−3])dp[i]=max(2×(i−2),2×dp[i−2],3×(i−3),3×dp[i−3])dp[i]=max(2×(i−2),2×dp[i−2],3×(i−3),3×dp[i−3])
class Solution:def integerBreak(self, n: int) -> int:if n <= 3:return n - 1dp = [0] * (n + 1)dp[2] = 1for i in range(3, n + 1):dp[i] = max(2 * (i - 2), 2 * dp[i - 2], 3 * (i - 3), 3 * dp[i - 3])return dp[n]
3.4.2 只有两个键的键盘
650. 只有两个键的键盘
最初记事本上只有一个字符 'A'。你每次可以对这个记事本进行两种操作:
- Copy All(复制全部):复制这个记事本中的所有字符(不允许仅复制部分字符)。
- Paste(粘贴):粘贴上一次复制的字符。
现在,给定一个数字 nnn,需要使用最少的操作次数,在记事本上输出恰好 nnn 个 'A' ,请返回能够打印出 nnn 个 'A' 的最少操作次数。
-
1≤n≤10001 \le n \le 10001≤n≤1000。
-
示例:
输入:3
输出:3
解释
最初, 只有一个字符 'A'。
第 1 步, 使用 Copy All 操作。
第 2 步, 使用 Paste 操作来获得 'AA'。
第 3 步, 使用 Paste 操作来获得 'AAA'。
思路 1:动态规划
class Solution(object):def minSteps(self, n):""":type n: int:rtype: int"""if n==1:return 0elif n==2:return 2dp=[i for i in range(n+1)] # 每次复制一个,n至多操作n次dp[0]=0dp[1]=0dp[2]=2for i in range(3,n+1):for j in range(1,i):if i%j==0:dp[i]=min(dp[i],dp[j]+i//j)return dp[n]
其实j是i的因子,所以j应该不超过i\sqrt{i}i 。 将其优化:
- 划分阶段
按照字符 'A' 的个数进行阶段划分。
- 定义状态
定义状态 dp[i]dp[i]dp[i] 表示为:通过「复制」和「粘贴」操作,得到 iii 个字符 'A',最少需要的操作数。
-
状态转移方程
- 对于 iii 个字符
'A',如果 iii 可以被一个小于 iii 的整数 jjj 除尽(jjj 是 iii 的因子),则说明 jjj 个字符'A'可以通过「复制」+「粘贴」总共 ij\frac{i}{j}ji 次得到 iii 个字符'A'。 - 而得到 jjj 个字符
'A',最少需要的操作数可以通过 dp[j]dp[j]dp[j] 获取。
- 对于 iii 个字符
则我们可以枚举 iii 的因子,从中找到在满足 jjj 能够整除 iii 的条件下,最小的 dp[j]+ijdp[j] + \frac{i}{j}dp[j]+ji,即为 dp[i]dp[i]dp[i],即 dp[i]=minj∣i(dp[i],dp[j]+ij)dp[i] = min_{j | i}(dp[i], dp[j] + \frac{i}{j})dp[i]=minj∣i(dp[i],dp[j]+ji)。
由于 jjj 能够整除 iii,则 jjj 与 ij\frac{i}{j}ji 都是 iii 的因子,两者中必有一个因子是小于等于 i\sqrt{i}i 的,所以在枚举 iii 的因子时,我们只需要枚举区间 [1,i][1, \sqrt{i}][1,i] 即可。
综上所述,状态转移方程为:dp[i]=minj∣i(dp[i],dp[j]+ij,dp[ij]+j)dp[i] = min_{j | i}(dp[i], dp[j] + \frac{i}{j}, dp[\frac{i}{j}] + j)dp[i]=minj∣i(dp[i],dp[j]+ji,dp[ji]+j)
-
初始条件
当 i=1i = 1i=1 时,最少需要的操作数为 000。所以 dp[1]=0dp[1] = 0dp[1]=0。 -
最终结果
根据我们之前定义的状态,dp[i]dp[i]dp[i] 表示为:通过「复制」和「粘贴」操作,得到 iii 个字符'A',最少需要的操作数。 所以最终结果为 dp[n]dp[n]dp[n]。
import mathclass Solution:def minSteps(self, n: int) -> int:dp = [0 for _ in range(n + 1)]for i in range(2, n + 1):dp[i] = float('inf')for j in range(1, int(math.sqrt(n)) + 1):if i % j == 0:dp[i] = min(dp[i], dp[j] + i // j, dp[i // j] + j)return dp[n]
- 时间复杂度:O(nn)O(n \sqrt{n})O(nn)。外层循环遍历的时间复杂度是 O(n)O(n)O(n),内层循环遍历的时间复杂度是 O(n)O(\sqrt{n})O(n),所以总体时间复杂度为 O(nn)O(n \sqrt{n})O(nn)。
- 空间复杂度:O(n)O(n)O(n)。用到了一维数组保存状态,所以总体空间复杂度为 O(n)O(n)O(n)。
3.5 线性 DP 题目大全
单串线性 DP 问题
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0300 | 最长递增子序列 | Python | 二分查找、动态规划 | 中等 |
| 0673 | 最长递增子序列的个数 | Python | 动态规划 | 中等 |
| 0354 | 俄罗斯套娃信封问题 | Python | 动态规划、二分查找 | 困难 |
| 0053 | 最大子数组和 | Python | 数组、分治算法、动态规划 | 简单 |
| 0152 | 乘积最大子数组 | Python | 数组、动态规划 | 中等 |
| 0918 | 环形子数组的最大和 | Python | 数组、动态规划 | 中等 |
| 0198 | 打家劫舍 | Python | 动态规划 | 中等 |
| 0213 | 打家劫舍 II | Python | 动态规划 | 中等 |
| 0740 | 删除并获得点数 | |||
| 1388 | 3n 块披萨 | |||
| 0873 | 最长的斐波那契子序列的长度 | Python | 数组、哈希表、动态规划 | 中等 |
| 1027 | 最长等差数列 | |||
| 1055 | 形成字符串的最短路径 | |||
| 0368 | 最大整除子集 | |||
| 0032 | 最长有效括号 | Python | 栈、字符串、动态规划 | 困难 |
| 0413 | 等差数列划分 | |||
| 0091 | 解码方法 | Python | 字符串、动态规划 | 中等 |
| 0639 | 解码方法 II | Python | 字符串、动态规划 | 困难 |
| 0132 | 分割回文串 II | |||
| 1220 | 统计元音字母序列的数目 | Python | 动态规划 | 困难 |
| 0338 | 比特位计数 | Python | 位运算、动态规划 | 简单 |
| 0801 | 使序列递增的最小交换次数 | Python | 动态规划 | 中等 |
| 0871 | 最低加油次数 | |||
| 0045 | 跳跃游戏 II | Python | 贪心、数组、动态规划 | 中等 |
| 0813 | 最大平均值和的分组 | |||
| 0887 | 鸡蛋掉落 | Python | 数学、二分查找、动态规划 | 困难 |
| 0256 | 粉刷房子 | |||
| 0265 | 粉刷房子 II | |||
| 1473 | 粉刷房子 III | |||
| 0975 | 奇偶跳 | |||
| 0403 | 青蛙过河 | Python | 数组、动态规划 | 困难 |
| 1478 | 安排邮筒 | |||
| 1230 | 抛掷硬币 | |||
| 0410 | 分割数组的最大值 | Python | 二分查找、动态规划 | 困难 |
| 1751 | 最多可以参加的会议数目 II | |||
| 1787 | 使所有区间的异或结果为零 | |||
| 0121 | 买卖股票的最佳时机 | Python | 数组、动态规划 | 简单 |
| 0122 | 买卖股票的最佳时机 II | Python | 数组、贪心算法 | 简单 |
| 0123 | 买卖股票的最佳时机 III | Python | 数组、动态规划 | 困难 |
| 0188 | 买卖股票的最佳时机 IV | Python | 数组、动态规划 | 困难 |
| 0309 | 最佳买卖股票时机含冷冻期 | Python | 数组、动态规划 | 中等 |
| 0714 | 买卖股票的最佳时机含手续费 | Python | 贪心、数组、动态规划 | 中等 |
双串线性 DP 问题
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 1143 | 最长公共子序列 | Python | 字符串、动态规划 | 中等 |
| 0712 | 两个字符串的最小ASCII删除和 | |||
| 0718 | 最长重复子数组 | Python | 数组、二分查找、动态规划、滑动窗口、哈希函数、滚动哈希 | 中等 |
| 0583 | 两个字符串的删除操作 | Python | 字符串、动态规划 | 中等 |
| 0072 | 编辑距离 | Python | 字符串、动态规划 | 困难 |
| 0044 | 通配符匹配 | Python | 贪心、递归、字符串、动态规划 | 困难 |
| 0010 | 正则表达式匹配 | Python | 递归、字符串、动态规划 | 困难 |
| 0097 | 交错字符串 | |||
| 0115 | 不同的子序列 | Python | 字符串、动态规划 | 困难 |
| 0087 | 扰乱字符串 |
矩阵线性 DP 问题
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0118 | 杨辉三角 | Python | 数组 | 简单 |
| 0119 | 杨辉三角 II | Python | 数组 | 简单 |
| 0120 | 三角形最小路径和 | Python | 数组、动态规划 | 中等 |
| 0064 | 最小路径和 | Python | 数组、动态规划、矩阵 | 中等 |
| 0174 | 地下城游戏 | |||
| 0221 | 最大正方形 | Python | 数组、动态规划、矩阵 | 中等 |
| 0931 | 下降路径最小和 | |||
| 0576 | 出界的路径数 | Python | 动态规划 | 中等 |
| 0085 | 最大矩形 | |||
| 0363 | 矩形区域不超过 K 的最大数值和 | |||
| 面试题 17.24 | 最大子矩阵 | |||
| 1444 | 切披萨的方案数 |
无串线性 DP 问题
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 1137 | 第 N 个泰波那契数 | Python | 记忆化搜索、数学、动态规划 | 简单 |
| 0650 | 只有两个键的键盘 | Python | 数学、动态规划 | 中等 |
| 0264 | 丑数 II | Python | 哈希表、数学、动态规划、堆(优先队列) | 中等 |
| 0279 | 完全平方数 | Python | 广度优先搜索、数学、动态规划 | 中等 |
| 0343 | 整数拆分 | Python | 数学、动态规划 | 中等 |
相关文章:

LeetCode练习七:动态规划上:线性动态规划
文章目录一、 动态规划基础知识1.1 动态规划简介1.2 动态规划的特征1.2.1 最优子结构性质1.2.2 重叠子问题性质1.2.3 无后效性1.3 动态规划的基本思路1.4 动态规划基础应用1.4.1 斐波那契数1.4.2 爬楼梯1.4.3 不同路径1.5 个人总结二、记忆化搜索2.1 记忆化搜索简介2.2 记忆化搜…...

基于正点原子F407开发版和SPI接口屏移植touchgfx完整教程(一)
一、相关软件包安装 1、打开cubemx包管理器 2、安装F4软件包 3、安装touchgfx软件包 二、工程配置 1、新建工程 2、sys配置 3、rcc配置 4、crc配置 5、添加touchgfx软件包 6、配置touchgfx软件包 将width和height改为自己屏幕尺寸 7、生成工程 三、代码修改 1、将屏幕相关驱…...

Linux--进程间通信
前言 上一篇相关Linux文章已经时隔2月,Linux的学习也相对于来说是更加苦涩;无妨,漫漫其修远兮,吾将上下而求索。 下面该片文章主要是对进程间通信进行介绍,还对管道,消息队列,共享内存,信号量都…...

hadoop伪分布式集群搭建
基于hadoop 3.1.4 一、准备好需要的文件 1、hadoop-3.1.4编译完成的包 链接: https://pan.baidu.com/s/1tKLDTRcwSnAptjhKZiwAKg 提取码: ekvc 2、需要jdk环境 链接: https://pan.baidu.com/s/18JtAWbVcamd2J_oIeSVzKw 提取码: bmny 3、vmware安装包 链接: https://pan.baidu…...

Qt 中的信息输出机制:QDebug、QInfo、QWarning、QCritical 的简单介绍和用法
Qt 中的信息输出机制介绍QDebug在 Qt 中使用 qDebug输出不同类型的信息浮点数:使用 %!f(MISSING) 格式化符号输出浮点数布尔值:使用 %! (MISSING)和 %! (MISSING)格式化符号输出布尔值对象:使用 qPrintable() 函数输出对象的信息qInfoqWarnin…...

C++读写excel文件的的第三方库
一、比较流行的库 1. OpenXLSX 用于读取、写入、创建和修改 Microsoft Excel (.xlsx) 文件的 C 库。 2. xlnt xlnt 是一个现代 C 库,用于操作内存中的电子表格以及从 XLSX 文件读取/写入它们,如ECMA 376 第 4 版中所述。xlnt 1.0 版的首次公开发布是在 …...
【关于Linux中----多线程(一)】
文章目录认识线程创建线程线程优点和缺点创建一批线程终止线程线程的等待问题认识线程 在一个程序里的一个执行路线就叫做线程(thread)。更准确的定义是:线程是“一个进程内部的控制序列”一切进程至少都有一个执行线程线程在进程内部运行&a…...

2023年全国最新安全员精选真题及答案34
百分百题库提供安全员考试试题、建筑安全员考试预测题、建筑安全员ABC考试真题、安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.(单选题)物料提升机附墙架设置要符合设计要求,但…...

数据出境是什么意思?我国数据出境合规要求是什么?
随着经济全球化深入以及云计算等技术的发展,数据在全球范围跨境流动。数据跨境在促进经济增长、加速创新的同时,对数据主权、数据权属、个人信息保护等一系列问题逐渐浮出水面。今天我们就先来了解一下数据出境是什么意思?我国数据出境合规要…...
Liunx——Git工具使用
目录 1)使用 git 命令行安装 git 2)在 Gitee 创建仓库 创建仓库 3)Linux克隆仓库到本地 4)提交代码三板斧: 1.三板斧第一招: git add 2.三板斧第二招: git commit 3.三板斧第三招: git push 5)所遇…...

微软语音合成工具+基于Electron + Vue + ElementPlus + Vite 构建并能将文字转换为语音 MP3
微软语音合成工具基于Electron Vue ElementPlus Vite 构建并能将文字转换为语音 MP3 资源下:微软语音合成工具基于ElectronVueElementPlusVite构建并能将文字转换为语音MP3资源-CSDN文库 本文将介绍如何使用微软语音合成工具和前端技术栈进行开发,…...
Mongodb学习笔记2
文章目录前言一、搭建项目二、开始编写java代码1. 新增2.查询3. 修改4. 删除5.根据条件查询6. 关联查询7. 索引相关总结前言 MongoTemplate 相关操作 CRUD,聚合查询等; 一、搭建项目 springboot项目创建引入mongo 依赖docker 安装好mongo数据库配置yml 链接mongo spring:dat…...

学习Tensorflow之基本操作
学习Tensorflow之基本操作Tensorflow基本操作1. 创建张量(1) 创建标量(2) 创建向量(3) 创建矩阵(4) shape属性(5) 判别张量类型(6) 列表和ndarray转张量2. 创建特殊张量(1) tf.ones与tf.ones_like(2) tf.zeros与tf.zeros_like(3) tf.fill(3) tf.random.normal(4) tf.random.uni…...
《Spring系列》第2章 解析XML获取Bean
一、基础代码 Spring加载bean实例的代码 public static void main(String[] args) throws IOException {// 1.获取资源Resource resource new ClassPathResource("bean.xml");// 2.获取BeanFactoryDefaultListableBeanFactory factory new DefaultListableBeanFa…...

小红书20230326暑假实习笔试
第一题:加密 小明学会了一种加密方式。他定义suc(x)为x在字母表中的后继,例如a的后继为b,b的后继为c… (即按字母表的顺序后一个)。特别的,z的后继为a。对于一个原字符串S,将其中每个字母x都替…...
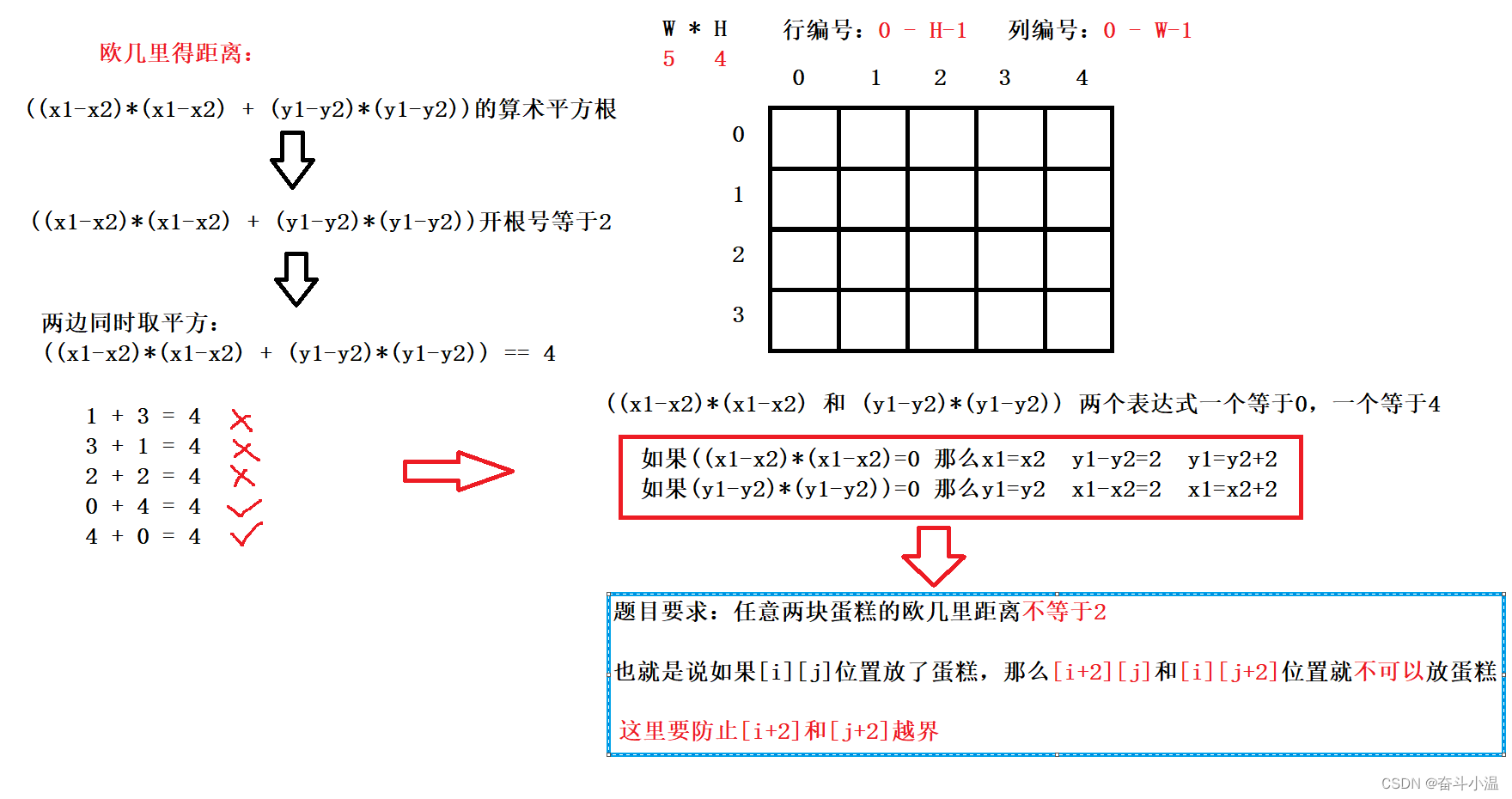
【java】不要二、把字符串转成整数
目录 🔥一、编程题 1.不要二 2.把字符串转换成整数 🔥一、编程题 1.不要二 链接:不要二_牛客题霸_牛客网 (nowcoder.com) 描述:二货小易有一个W*H的网格盒子,网格的行编号为0~H-1,网格的列编号为0~W-1…...

数据的质量管控工作
数据的质量管控工作,整个工作应该围绕启动阶段制定的目标进行。适当引入一些质量管控工具可帮助我们更高效的完成工作。 第一步、数据剖析 首先应该进行已知数据问题的评估,这里评估的范围也应控制本轮管控的目标范围内。其次,通过对数据进行…...

【SpringBoot笔记29】SpringBoot集成RabbitMQ消息队列
这篇文章,主要介绍SpringBoot如何集成RabbitMQ消息队列。 目录 一、集成RabbitMQ 1.1、引入amqp依赖 1.2、添加连接信息 1.3、添加RabbitMQ配置类...

前端架构师-week2-脚手架架构设计和框架搭建
将收获什么 脚手架的实现原理 Lerna的常见用法 架构设计技巧和架构图绘制方法 主要内容 学习如何以架构师的角度思考基础架构问题 多 Package 项目管理痛点和解决方案,基于 Lerna 脚手架框架搭建 imooc-cli 脚手架需求分析和架构设计,架构设计图 附赠内…...

CMake项目实战指令详细分析
CMake是一个跨平台的自动化构建系统,可以用简单的语句来描述所有平台的编译过程。CMake可以输出各种各样的编译文件,如Makefile、VisualStudio等。 CMake主要是编写CMakeLists.txt文件,然后用cmake命令将CMakeLists.txt文件转化为make所需要的…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
