关于最小二乘法
最小二乘法的核心思想简单而优雅:我们希望找到一条最佳的曲线,使其尽可能贴近所有的数据点。想象一下,当你在画布上描绘一条线,目标是让这条线与点的距离最小。数学上,这可以表示为:

在这个公式中,yi 是你观察到的值,f(xi) 则是你预测的值。通过调整模型的参数,我们努力去缩小这个误差的平方和,直到找到最完美的曲线。
多项式回归
如果说线性回归是最小二乘法的基础,那么多项式回归则为它增添了丰富的层次。通过将数据点拟合成一条曲线,我们可以捕捉到更复杂的趋势。比如,二次回归模型能够揭示数据中潜藏的非线性关系,让我们看到更真实的画面。
非线性最小二乘法
生活中的许多现象并不是线性的,这时非线性最小二乘法便应运而生。它能处理如指数、对数等更为复杂的关系,为我们打开新的视野。使用牛顿法、拟牛顿法等优化算法,我们能够精准地找到适合的参数,揭示数据的深层次关系。
加权最小二乘法
在某些情况下,数据的可靠性并不相同。加权最小二乘法允许我们为每个观测值赋予不同的权重。这就像是在选举中,有些选票比其他选票更有影响力。通过这种方式,我们能够更精准地反映数据的重要性。
应用的广阔天地
最小二乘法的应用场景几乎无处不在。它在社会科学中帮助我们分析教育与收入之间的关系;在经济学中,它帮助预测通货膨胀率和GDP增长;在工程领域,它优化了信号处理和控制系统的设计。甚至在医学研究中,它为评估治疗效果与患者特征的关系提供了有力支持。
Python 实现
接下来,我们来看看如何用Python实现简单的线性回归,利用最小二乘法来拟合数据。
代码示例
import numpy as np
import matplotlib.pyplot as plt# 创建一些示例数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([2.2, 2.8, 3.6, 4.5, 5.1])# 计算最小二乘法的参数
A = np.vstack([x, np.ones(len(x))]).T
m, b = np.linalg.lstsq(A, y, rcond=None)[0]# 绘制结果
plt.scatter(x, y, color='blue', label='数据点')
plt.plot(x, m*x + b, color='red', label='拟合线')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('最小二乘法线性回归')
plt.show()print(f"斜率: {m}, 截距: {b}")
代码解析
- 数据准备:首先,我们创建了一组示例数据点。
x是自变量,y是因变量。 - 构建设计矩阵:我们将自变量和常数项组合成一个设计矩阵 AAA,以便进行线性回归。
- 计算最小二乘法参数:使用 NumPy 的
lstsq函数,我们计算出最佳拟合线的斜率 mmm 和截距 bbb。 - 绘图:最后,我们用 Matplotlib 绘制数据点和拟合线,使结果一目了然。
现代数据科学中的重要性
在当今这个信息爆炸的时代,数据的海洋中充满了复杂性与不确定性。最小二乘法作为一种基础工具,依然具有不可替代的地位。它不仅使我们能够从纷繁复杂的数据中提炼出有价值的信息,更为许多机器学习算法提供了理论基础。它的易用性和高效性使得初学者能够快速上手,而其深厚的理论支持又让研究者得以深入探索。
这个看似简单的工具,实则蕴含着深刻的数学智慧。希望这篇文章能让你在日后的数据探索中,感受到最小二乘法的力量与魅力,助你在复杂的世界中找到那条最优的路径。
相关文章:

关于最小二乘法
最小二乘法的核心思想简单而优雅:我们希望找到一条最佳的曲线,使其尽可能贴近所有的数据点。想象一下,当你在画布上描绘一条线,目标是让这条线与点的距离最小。数学上,这可以表示为: 在这个公式中ÿ…...

国产OpenEuler与Centos全面之比较
OpenEuler 和 CentOS 都是流行的 Linux 发行版,但它们有一些关键的区别。以下是 OpenEuler 和 CentOS 的全面比较: 1. 起源和支持: - OpenEuler:由华为公司支持,中国开源社区主导开发的操作系统,旨在构建一…...

Java面试题一
一、Java语言有哪些特性? Java语言具有多种特性,这些特性使得Java成为一种广泛使用的编程语言。以下是Java语言的一些主要特性: 面向对象(Object-Oriented): Java是一种纯面向对象的编程语言。它支持类&…...
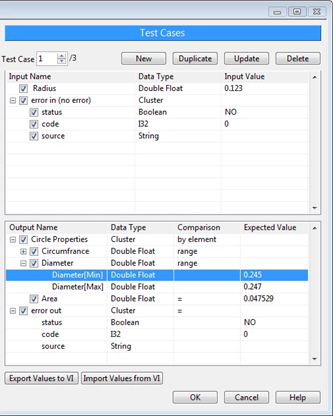
LabVIEW提高开发效率技巧----自动化测试和持续集成
在大型项目中,自动化测试和持续集成是提高开发效率和代码质量的关键手段。通过这些技术,开发者能够在开发的早期阶段快速发现问题,减少后期调试的工作量,并且能够确保代码的稳定性和可维护性。以下是这两个概念如何在LabVIEW开发中…...

开源链动 2+1 模式 S2B2C 商城小程序:激活 KOC,开启商业新征程
摘要:本文深入探讨了 KOC 在立体连接中的重要性,以及如何通过开源链动 21 模式 S2B2C 商城小程序发现和找到更多的 KOC。强调了历史积累强关系和快速强化强关系的方法,并阐述了该商城小程序在推动商业发展中的关键作用。 一、引言 在当今竞争…...

什么是Node.js?
为什么JavaScript可以在浏览器中被执行? 在浏览器中我们加载了一些待执行JS代码,这些字符串要当中一个代码去执行,是因为浏览器中有JavaScript的解析引擎,它的存在我们的代码才能被执行。 不同的浏览器使用不同的javaScript解析引…...

即插即用篇 | DenseNet卷土重来! YOLOv8 引入全新密集连接卷积网络 | ECCV 2024
本改进已同步到YOLO-Magic框架! 本文重新审视了密集连接卷积网络(DenseNets),并揭示了其在主流的ResNet风格架构中被低估的有效性。我们认为,由于未触及的训练方法和传统设计元素没有完全展现其能力,DenseNets的潜力被忽视了。我们的初步研究表明,通过连接实现的密集连接…...
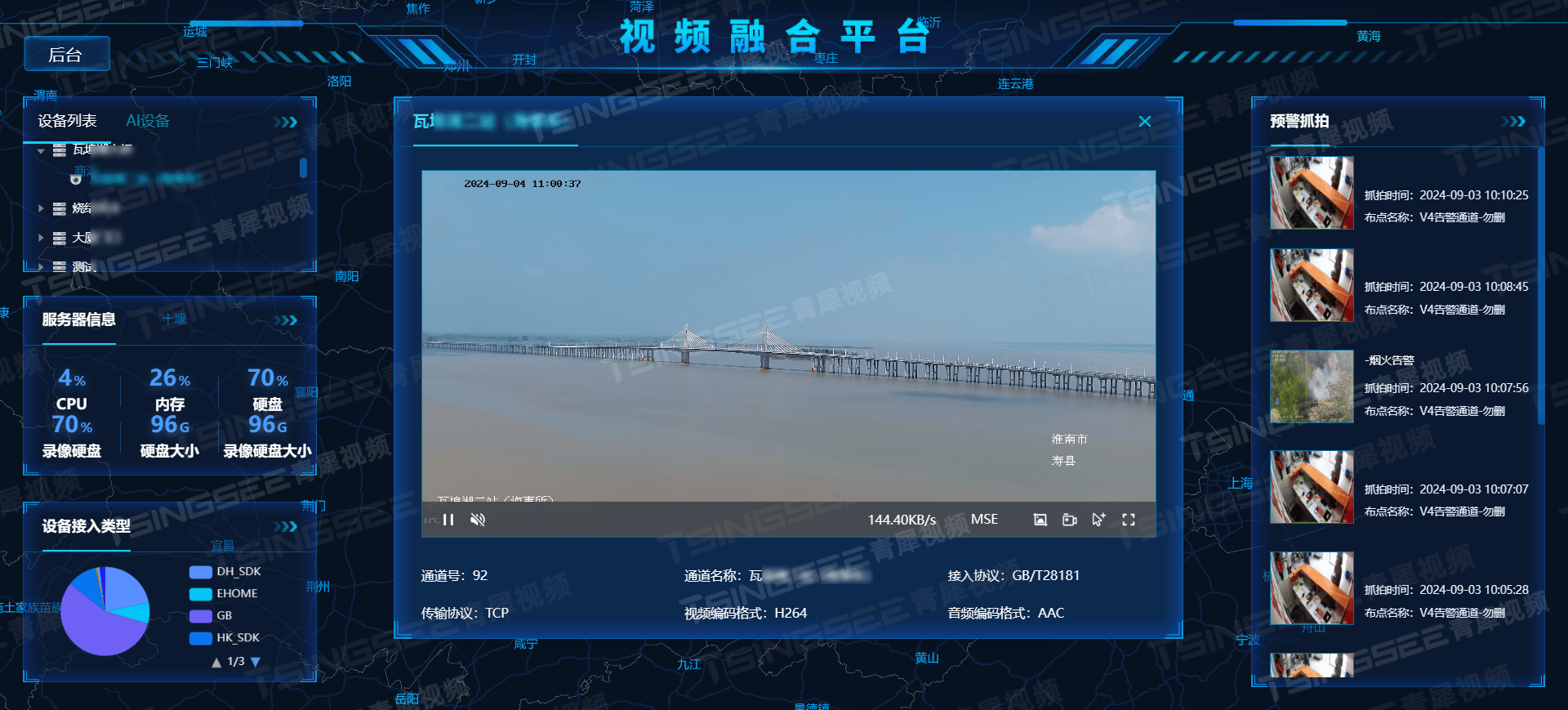
智能监控,守护绿色能源:EasyCVR在电站视频监控中心的一站式解决方案
随着科技的飞速发展,视频监控技术在社会安全、企业管理及智慧城市建设等领域中扮演着越来越重要的角色。特别是在电力行业中,电站作为能源供应的关键设施,其安全性和稳定性至关重要。传统的人工监控方式已难以满足现代电站复杂多变的运行需求…...

【BUG】静读天下|静读天下无法设置段间距解决方案
【BUG】静读天下|静读天下无法设置段间距解决方案 文章目录 【BUG】静读天下|静读天下无法设置段间距解决方案前言解决办法 凑质量分静读天下的特点与优势功能布局与使用技巧个人使用心得结语 前言 03-23 求助|关于排版的问题【静读天下吧】_…...

希捷电脑硬盘好恢复数据吗?探讨可能性、方法以及注意事项
在数字化时代,数据已成为我们生活和工作中不可或缺的一部分。希捷电脑硬盘作为数据存储的重要设备,承载着大量的个人文件、工作资料以及珍贵回忆。然而,面对硬盘故障或误操作导致的数据丢失,许多用户不禁要问:希捷电脑…...

java通过webhook给飞书发送群消息
现在使用飞书的人越来越多了,飞书有一个最大的好处,可以使用webhook简便的发送群消息。而在工作中,也经常会因为一些运维方面的工作,需要给飞书发送群消息,来实时提醒相关负责人,及时处理工作。 一、先看一下效果吧&a…...

每日一题——第一百零九题
题目:进制转换合集。任意r进制与十进制之间的转换 #include<stdio.h> #include<stdlib.h> #include<string.h> #include<ctype.h> long stringToDecimal(const char* str, int base); void convertToBaseR(int num, int r);int main() {ch…...

街头摊贩检测系统源码分享
街头摊贩检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of Computer Vis…...

服务器数据恢复—SAN环境下LUN映射出错导致文件系统一致性出错的数据恢复案例
服务器数据恢复环境: SAN环境下一台存储设备中有一组由6块硬盘组建的RAID6磁盘阵列,划分若干LUN,MAP到不同业务的SOLARIS操作系统服务器上。 服务器故障: 用户新增了一台服务器,将存储中的某个LUN映射到新增加的这台服…...

深度学习:自然语言处理的基本原理
概念: 自然语言处理(Natural Language Processing,简称NLP)是人工智能和语言学领域的一个分支,它致力于研究如何让计算机能够理解、解释和生成人类语言,以及如何实现人与计算机之间的有效通信。自然语言处理…...

Win10 Chrome浏览器被强制绑定主页的解决办法
Win10 Chrome浏览器被强制绑定主页的解决办法 背景 刚刚重装的系统默认是某杀毒软件,使用浏览器时发现浏览器主页老是hao123,还改不了。于是卸载了此杀毒软件,换了别的。发现还是解决不了浏览器主页被绑定且改不了的问题 体现 chrome://se…...

【UE5】将2D切片图渲染为体积纹理,最终实现使用RT实时绘制体积纹理【第四篇-着色器投影-接收阴影部分】
上一章中实现了体积渲染的光照与自阴影,那我们这篇来实现投影 回顾 勘误 在开始本篇内容之前,我已经对上一章中的内容的错误进行了修改。为了确保不会错过这些更正,同时也避免大家重新阅读一遍,我将在这里为大家演示一下修改的…...

Shell脚本基础——实训项目任务
项目一 项目实训 (初始Shell脚本) 项目一 项目实训 (初始Shell脚本)项目实施任务一 输入输出重定向任务二 数据输入输出操作任务三 Shell变量操作任务四 算术运算符操作任务五 设置环境变量 【实训任务】 本实训的主要任务是通过编写简单的shell脚本,完成使用数据…...
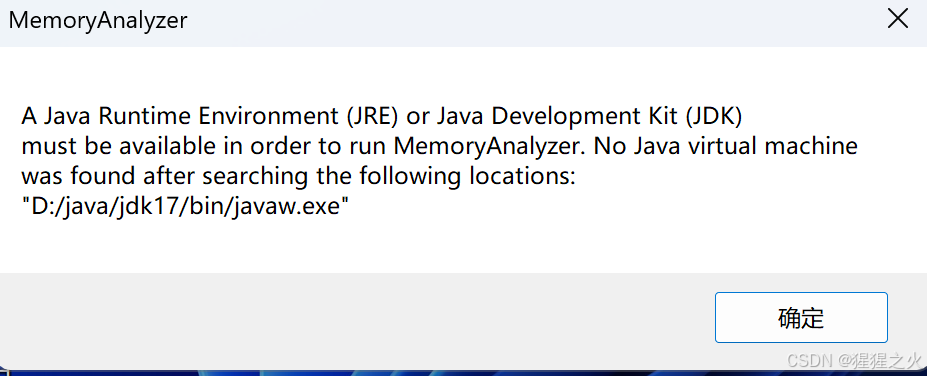
Eclipse Memory Analyzer (MAT)提示No java virtual machine was found ...解决办法
1,下载mat后安装,打开时提示 jdk版本低,需要升级到jdk17及以上版本,无奈就下载了jdk17,结果安装后提示没有jre环境,然后手动生成jre目录,命令如下: 进入jdk17目录:执行&…...

【C++篇】深度剖析C++ STL:玩转 list 容器,解锁高效编程的秘密武器
文章目录 C list 容器详解:从入门到精通前言第一章:C list 容器简介1.1 C STL 容器概述1.2 list 的特点 第二章:list 的构造方法2.1 常见构造函数2.1.1 示例:不同构造方法2.1.2 相关文档 第三章:list 迭代器的使用3.1 …...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
