Acwing 最小生成树
最小生成树
最小生成树:由n个节点,和n-1条边构成的无向图被称为G的一棵生成树,在G的所有生成树中,边的权值之和最小的生成树,被称为G的最小生成树。(换句话说就是用最小的代价把n个点都连起来)
- Prim 算法(普利姆)
-
- 朴素版Prim(时间复杂度 O ( n 2 ) O(n^2) O(n2),适用于稠密图;
-
- 堆优化版Prim(时间复杂度 O ( m l o g n ) O(m log n) O(mlogn),适用于稀疏图),基本不用;
- Kruskal算法,适用于稀疏图,时间复杂度 O ( m l o g m ) O(m log m) O(mlogm).$
如果是稠密图,通常选用朴素版Prim算法,因为其思路比较简洁,代码比较短;如果是稀疏图,通常选用Kruskal算法,因为其思路比Prim简单清晰。堆优化版的Prim通常不怎么用。
1.Prim
朴素Prim
与朴素dijkstra思想几乎一样,只不过Prim算法的距离指得是点到最小生成树的集合的距离,而Dijkstra算法的距离是点到起点的距离。适合用于稠密图
Prim 算法过程:
- 初始化 dist 数组,表示各点到最小生成树的距离。开始时设为无穷大(INF)。
- 使用贪心策略,每次选取距离集合最近的点 t,并将其加入最小生成树。
- 若该点距离 INF 且不是第一个节点,表示图不连通,直接返回 INF。
- 更新其余未加入集合的点与最小生成树的最短距离。
- 最终返回最小生成树的总权值,若图不连通则输出 impossible。
实现思路:
- 初始化各点到集合的距离INF;
- n次循环,每次找到集合外且距离集合最近的点t,需要先判断除第一个点外找到的距离最近的点t距离是不是INF;
-
- 若是则不存在最小生成树了,结束;否则还可能存在,继续操作,用该点t来更新其它点到集合的距离(这里就是和Dijkstra最主要的区别),然后将该点t加入集合;
- 关于集合到距离最近的点:实际上就是不在集合的点与集合内的点的各个距离的最小值,每次加入新的点都会尝试更新一遍(dist[j] = min(dist[j],g[t][j]).在Dijkstra中是dist[j] - min(dits[j],dist[t] + g[t][j]));

板子:
const int N = 510, INF = 0x3f3f3f3f; // 定义最大节点数 N 和无穷大 INF
int g[N][N], dist[N]; // g[i][j] 表示从节点 i 到节点 j 的边权,dist[i] 表示当前生成树到节点 i 的最短距离
bool st[N]; // st[i] 表示节点 i 是否已经加入到最小生成树中int n, m; // n 表示节点数量,m 表示边的数量// 返回最小生成树的权值之和。如果图不连通,返回 INF
int prim() {memset(dist, 0x3f, sizeof dist); // 初始化所有节点的最短距离为 INF(即无穷大)int res = 0; // 最终的最小生成树权值之和// Prim 算法的核心,循环 n 次,每次找到一个未加入集合的最近节点for (int i = 0; i < n; i++) {int t = -1; // 用于记录当前找到的距离最小的节点// 找到距离当前生成树最近的未加入集合的节点for (int j = 1; j <= n; j++) {if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;}// 如果当前是第一个节点或者找到的节点距离集合为 INF,说明图不连通if (i && dist[t] == INF) return INF; // 无法构成最小生成树if (i) res += dist[t]; // 将该节点的边权值加入最终结果中// 更新其他未加入集合的节点到生成树的最短距离for (int j = 1; j <= n; j++) {dist[j] = min(dist[j], g[t][j]); // 使用该节点 t 更新其他节点的最短距离}st[t] = true; // 标记该节点已经加入生成树}return res; // 返回最小生成树的总权值
}
Acwing 858.Prim 算法求最小生成树

注意:本题干未设起点所以要迭代n次,并且图中可能存在负的自环,因此计算最小生成树的总距离要在更新各点到集合距离之前。且该图为无向图,含重边,则构建边需要注意。
具体实现代码(详解版):
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 510, INF = 0x3f3f3f3f; // 定义最大节点数 N 和无穷大 INF
int g[N][N], dist[N]; // g[i][j] 表示从节点 i 到节点 j 的边权,dist[i] 表示当前生成树到节点 i 的最短距离
bool st[N]; // st[i] 表示节点 i 是否已经加入到最小生成树中int n, m; // n 表示节点数量,m 表示边的数量// 返回最小生成树的权值之和。如果图不连通,返回 INF
int prim() {memset(dist, 0x3f, sizeof dist); // 初始化所有节点的最短距离为 INF(即无穷大)int res = 0; // 最终的最小生成树权值之和// Prim 算法的核心,循环 n 次,每次找到一个未加入集合的最近节点for (int i = 0; i < n; i++) {int t = -1; // 用于记录当前找到的距离最小的节点// 找到距离当前生成树最近的未加入集合的节点for (int j = 1; j <= n; j++) {if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;}// 如果当前是第一个节点或者找到的节点距离集合为 INF,说明图不连通if (i && dist[t] == INF) return INF; // 无法构成最小生成树if (i) res += dist[t]; // 将该节点的边权值加入最终结果中// 更新其他未加入集合的节点到生成树的最短距离for (int j = 1; j <= n; j++) {dist[j] = min(dist[j], g[t][j]); // 使用该节点 t 更新其他节点的最短距离}st[t] = true; // 标记该节点已经加入生成树}return res; // 返回最小生成树的总权值
}int main() {cin >> n >> m; // 输入节点数 n 和边数 mmemset(g, 0x3f, sizeof g); // 初始化邻接矩阵,所有边权值设为无穷大(表示节点间无边)// 输入每条边的信息,构建邻接矩阵while (m--) {int a, b, c;cin >> a >> b >> c;g[a][b] = g[b][a] = min(g[a][b], c); // 无向图,所以 g[a][b] 和 g[b][a] 相同}int t = prim(); // 调用 Prim 算法计算最小生成树的权值// 输出结果。如果返回的是 INF,说明图不连通,输出 "impossible"if (t == INF) puts("impossible");else cout << t << endl; // 否则输出最小生成树的权值return 0;
}堆优化Prim:思路和堆优化的Dijkstra思路基本一样,且基本不用,对于稀疏图,不如用Kruskal,这里略过
2. Kruskal
适用于稀疏图,时间复杂度 O ( m l o g m ) O(m log m) O(mlogm).Kruskal 算法是求解无向连通图的 最小生成树(MST)的经典算法。它的核心思想是通过贪心策略,按权值从小到大逐步选择边,确保不会产生环,直到选出 n-1 条边为止。整个过程涉及使用 并查集 来判断是否形成环
- 先将所有的边按照权重,从小到大排序;
- 从小到大枚举每条边(a,b,w)若a,b不连通,则将这条边加入集合中(将a点和b点连接起来)实质上是一个并查集的应用(两点之间加边,看两点是否存在一个连通块)
- 无需用邻接表、邻接矩阵存储图,直接使用结构体,表示边及其权值

板子:
const int N = 200010, INF = 0x3f3f3f3f;
int p[N]; // 并查集的父节点数组
int n, m; // n 表示节点数,m 表示边数// 边的结构体,表示一条边及其权值
struct Edge {int a, b, w; // a, b 为连接的两个节点,w 为权值// 重载小于运算符,用于按边权值升序排序bool operator<(const Edge &W) const {return w < W.w;}
} edges[N]; // 存储所有边// 并查集:寻找节点 x 所在集合的根节点
int find(int x) {if (p[x] != x) p[x] = find(p[x]); // 路径压缩,找到根节点并直接连接return p[x];
}// Kruskal 算法求最小生成树
int kruskal() {sort(edges, edges + m); // 按照边的权值升序排序for (int i = 1; i <= n; i++) p[i] = i; // 初始化并查集,每个节点的父节点是自己int res = 0, cnt = 0; // res 存储最小生成树的权值之和,cnt 记录最小生成树的边数// 遍历所有边for (int i = 0; i < m; i++) {int a = edges[i].a, b = edges[i].b, w = edges[i].w;// 找到两个节点的根节点a = find(a), b = find(b);if (a != b) { // 如果两点不在同一个集合中,说明它们不连通p[a] = b; // 将两点所在的集合合并res += w; // 累加这条边的权值cnt++; // 增加计数}}// 如果使用的边数不足 n-1,则说明图不连通,无法构成最小生成树if (cnt < n - 1) return INF;else return res; // 返回最小生成树的权值
}
具体实现代码(详解版):
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 200010, INF = 0x3f3f3f3f;
int p[N]; // 并查集的父节点数组
int n, m; // n 表示节点数,m 表示边数// 边的结构体,表示一条边及其权值
struct Edge {int a, b, w; // a, b 为连接的两个节点,w 为权值// 重载小于运算符,用于按边权值升序排序bool operator<(const Edge &W) const {return w < W.w;}
} edges[N]; // 存储所有边// 并查集:寻找节点 x 所在集合的根节点
int find(int x) {if (p[x] != x) p[x] = find(p[x]); // 路径压缩,找到根节点并直接连接return p[x];
}// Kruskal 算法求最小生成树
int kruskal() {sort(edges, edges + m); // 按照边的权值升序排序for (int i = 1; i <= n; i++) p[i] = i; // 初始化并查集,每个节点的父节点是自己int res = 0, cnt = 0; // res 存储最小生成树的权值之和,cnt 记录最小生成树的边数// 遍历所有边for (int i = 0; i < m; i++) {int a = edges[i].a, b = edges[i].b, w = edges[i].w;// 找到两个节点的根节点a = find(a), b = find(b);if (a != b) { // 如果两点不在同一个集合中,说明它们不连通p[a] = b; // 将两点所在的集合合并res += w; // 累加这条边的权值cnt++; // 增加计数}}// 如果使用的边数不足 n-1,则说明图不连通,无法构成最小生成树if (cnt < n - 1) return INF;else return res; // 返回最小生成树的权值
}int main() {cin >> n >> m; // 输入节点数和边数for (int i = 0; i < m; i++) {int a, b, w;cin >> a >> b >> w; // 输入每条边的两个端点 a, b 和边的权值 wedges[i] = {a, b, w}; // 存储边的信息}int t = kruskal(); // 调用 Kruskal 算法if (t == INF) puts("impossible"); // 如果返回值为 INF,说明图不连通else cout << t << endl; // 否则输出最小生成树的权值return 0;
}Kruskal 算法的核心思想:
- 贪心策略:每次选择权值最小的边,且不形成环;
- 并查集:用于快速检查两个节点是否已经连通,以及合并不同的连通集合。
3.对比总结

相关文章:

Acwing 最小生成树
最小生成树 最小生成树:由n个节点,和n-1条边构成的无向图被称为G的一棵生成树,在G的所有生成树中,边的权值之和最小的生成树,被称为G的最小生成树。(换句话说就是用最小的代价把n个点都连起来) Prim 算法…...

VIM简要介绍
安装 大多数 Linux 发行版和 macOS 都预装了 VIM。如果没有,你可以通过包管理器安装: Ubuntu/Debian: sudo apt-get install vimFedora: sudo dnf install vimmacOS: brew install vim(使用 Homebrew)Windows: 可以从 VIM 官网下…...

.NET 6.0 使用log4net配置日志记录方法
1.包管理器引入相关包 2.添加Log4net文件夹和log4net.config配置文件(配置文件属性设为始终复制)。 3.替换 log4net.config的内容(3.1与3.2选择一个就好,只是创建日志文件有所区别) 3.1: <?xml version"1.0" encoding"utf-8"?> <configuration…...

Unity角色控制及Animator动画切换如走跑跳攻击
Unity角色控制及 Animator动画切换如走跑跳攻击 目录 Unity角色控制及 一、 概念 1、角色控制 1) CharacterController(角色控制器) 2) CapsuleCollider + Rigidbody(使用物理刚体控制) 2、角色动画-Animation、Animator 1) 旧版动画系统...

JSP+Servlet+Mybatis实现列表显示和批量删除等功能
前言 使用JSP回显用户列表,可以进行批量删除(有删除确认步骤),和修改用户数据(用户数据回显步骤)使用servlet处理传递进来的请求参数,并调用dao处理数据并返回使用mybatis,书写dao层…...

Cannot read properties of undefined (reading ‘upgrade‘)
前端开发工具:VSCODE 报错信息: INFO Starting development server...10% building 2/2 modules 0 active ERROR TypeError: Cannot read properties of undefined (reading upgrade)TypeError: Cannot read properties of undefined (reading upgrade…...

javaJUC基础
JUC基础知识 多线程 管程 Monitor,也就是平时所说的锁。Monitor其实是一种同步机制,它的义务是保证(同一时间)只有一个线程可以访问被保护的数据和代码块,JVM中同步是基于进入和退出监视器(Monitor管程对…...

std::distance 函数介绍
std::distance 是 C 标准库中的一个函数模板,用于计算两个迭代器之间的距离。它的主要作用是返回从第一个迭代器到第二个迭代器之间的元素数量。这个函数对于不同类型的迭代器(如随机访问、双向、前向等)都能有效工作。 函数原型 template …...

如何在Windows和Linux之间实现粘贴复制
第一步 sudo apt-get autorremove open-vm-tools第二步 sudo apt-get update第三步 sudo apt-get install open-vm-tools-desktop第四步 一直按Y,希望执行 Y第四步 重启 reboot然后可以实现粘贴复制。...

【第十七章:Sentosa_DSML社区版-机器学习之异常检测】
【第十七章:Sentosa_DSML社区版-机器学习之异常检测】 机器学习异常检测是检测数据集中的异常数据的算子,一种高效的异常检测算法。它和随机森林类似,但每次选择划分属性和划分点(值)时都是随机的,而不是根…...

【Vue】为什么 Vue 不使用 React 的分片更新?
第一,首先时间分片是为了解决 CPU 进行大量计算的问题,因为 React 本身架构的问题,在默认的情况下更新会进行很多的计算,就算使用 React 提供的性能优化 API,进行设置,也会因为开发者本身的问题,…...
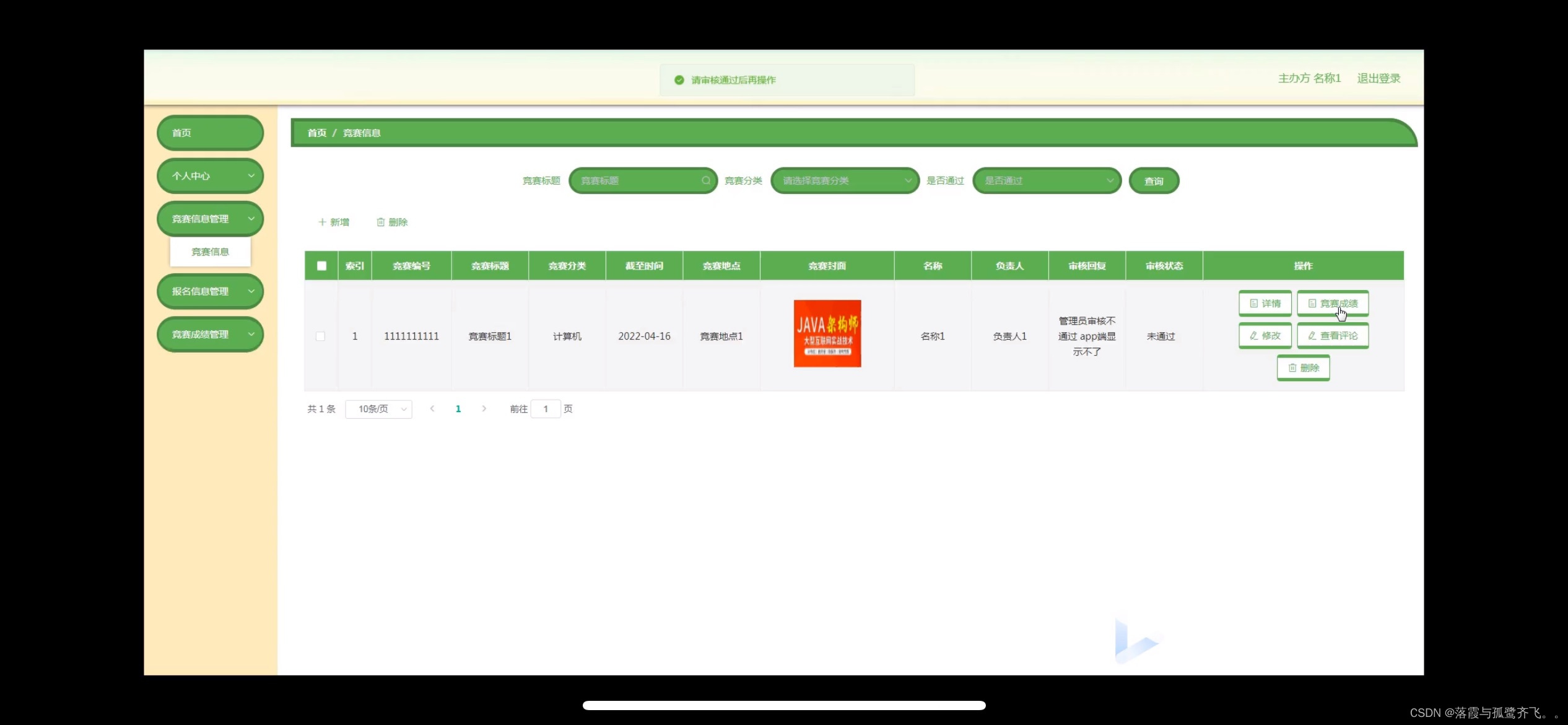
大学生科技竞赛系统小程序的设计
管理员账户功能包括:系统首页,个人中心,用户管理,主办方管理,公告栏管理,竞赛分类管理,竞赛信息管理,报名信息管理,竞赛成绩管理 微信端账号功能包括:系统首…...

什么是聚集索引?
什么是聚集索引? 1、聚集索引的特点2、如何确定聚集索引3、性能优势 💖The Begin💖点点关注,收藏不迷路💖 聚集索引是一种特殊的索引,它直接包含了表中的所有数据行。所以,通过聚集索引…...
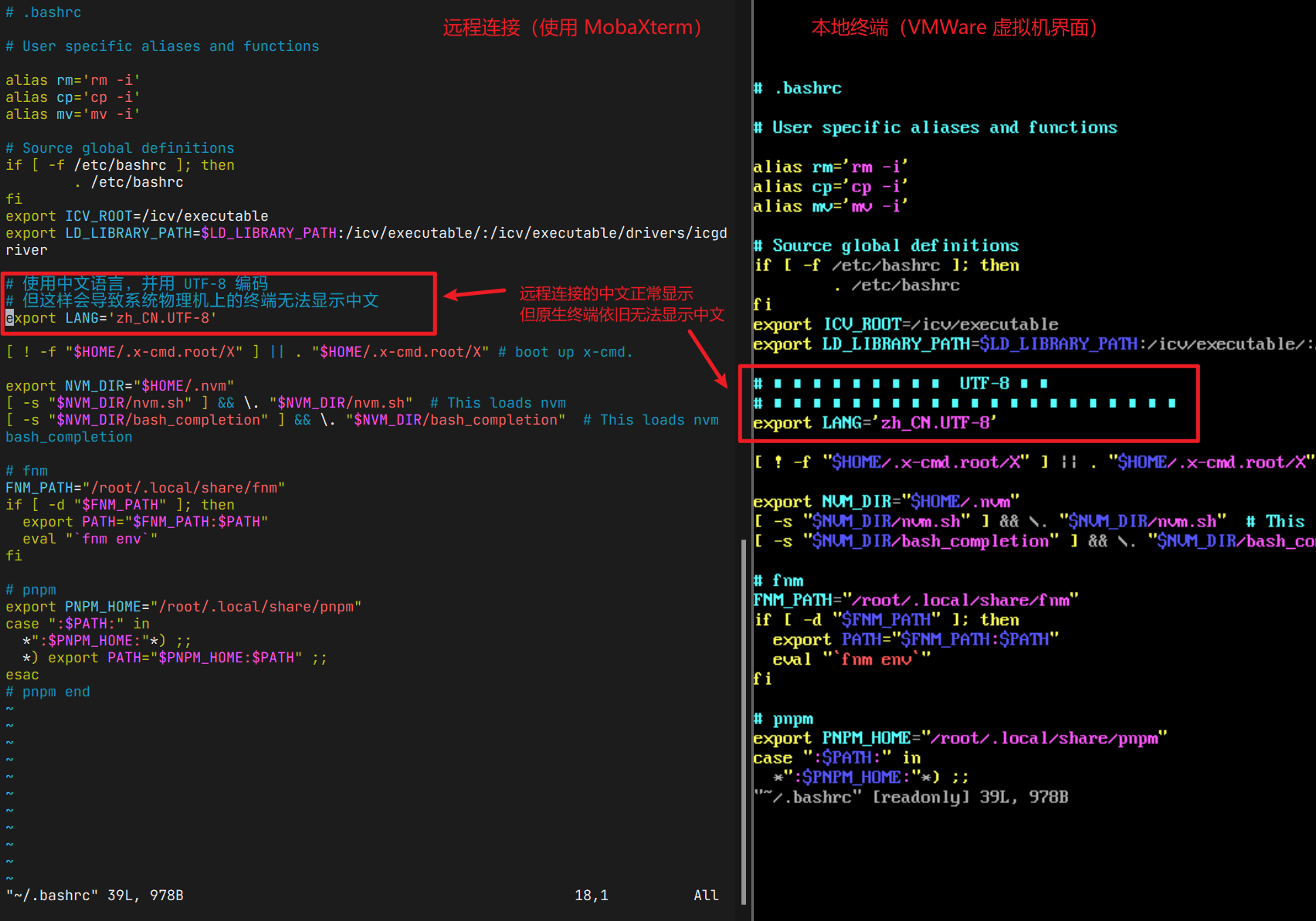
Centos/fedora/openEuler 终端中文显示配置
注意:这里主要解决的是图形界面、远程登录界面的中文乱码问题 系统原生的终端(如虚拟机系统显示的终端),由于使用的是十分原始的 TTY 终端,使用点阵字体进行显示,点阵字体不支持中文,因此无法显…...

使用kaggle命令下载数据集和模型
点击用户头像,点击Settings: 找到API,点击create new token,将自动下载kaggle.json: 在用户目录下创建.kaggle文件夹,并将下载的kaggle.json文件移动到该文件夹: cd ~ mv Downloads/kaggle.j…...

生信初学者教程(十一):数据校正
介绍 批次效应在生物学数据分析中是一个普遍存在的问题,它指的是由于实验过程中非生物学因素(如样本处理时间、实验条件、测序平台等)的差异,导致实验结果中混入与研究目标不相关的变异。在比较对照组和实验组时,这些非生物学因素可能引入额外的噪声,影响对生物学问题真实…...

JS设计模式之桥接模式:搭建跨越维度的通路
引言 在软件开发中,我们经常遇到需要对不同的抽象类进行不同的实现的情况,而传统的对象嵌套并不是一个优雅且可扩展的解决方案,因此这正是桥接模式的用武之地。桥接模式通过将抽象与实现分离,使得它们可以独立变化,从…...
苹果电脑系统重磅更新——macOS Sequoia 15 系统 新功能一 览
有了 macoS Sequoia,你的工作效率将再次提升:快速调整桌面布局,一目了然地浏览网页重点,还可以通过无线镜像功能操控你的iPhone。 下面就来看看几项出色新功能,还有能够全面发挥这些功能的 App 和游戏。 macOS Sequo…...

DoppelGanger++:面向数据库重放的快速依赖关系图生成
doi:DoppelGanger: Towards Fast Dependency Graph Generation for Database Replay,点击前往 文章目录 1 简介2 架构概述3 依赖关系图3.1 符号和问题定义3.2 无 IT(k) 图3.3 无 OT 图表3.4 无 OTIT 图表3.5 无 IT[OT] 图表3.6 输出确定性保证 4 重复向后…...

Linux(含麒麟操作系统)如何实现多显示器屏幕采集录制
技术背景 在操作系统领域,很多核心技术掌握在国外企业手中。如果过度依赖国外技术,在国际形势变化、贸易摩擦等情况下,可能面临技术封锁和断供风险。开发国产操作系统可以降低这种风险,确保国家关键信息基础设施的稳定运行。在一…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
