信息学奥赛一本通 1375:骑马修栅栏(fence) | 洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences
【题目链接】
ybt 1375:骑马修栅栏(fence)
洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences
【题目考点】
1. 图论:欧拉回路
- 欧拉回路存在的条件:图中所有顶点的度都是偶数
- 欧拉路径存在的条件:图中只有两个度为奇数的顶点。而且这两个顶点是欧拉路径的起点与终点。
求解欧拉回路使用Hierholzer算法
复杂度:O(V+E)O(V+E)O(V+E)
【解题思路】
该图是无向图,顶点就是图中的顶点,栅栏是边。
“栅栏都是连通的”,意味着这是一个无向连通图。
“使每个栅栏都恰好被经过一次”,就是每条边都经过一次。该问题为求欧拉路径。可以使用Hierholzer算法解决。
“两顶点间可能有多个栅栏”意味着可能有重边,但Hierholzer算法可以处理有重边或自环的图。
“输出500进制表示法中最小的一个”,即为输出字典序最小的欧拉路径顶点序列。
只需要在实现Hierholzer算法时,包括选择起始顶点或某顶点的邻接点时,尽量选择编号较小的顶点来访问即可。
在输入边时,统计顶点编号的最大值,作为总顶点数量。
首先从小到大遍历所有顶点
- 如果存在奇数度的顶点,选择该顶点作为起始点。
- 如果不存在奇数度的顶点,那么所有顶点的度都是偶数,任选顶点作为起始点。这里选择1号顶点为起始点。
从起始顶点出发,进行深搜,使用Hierholzer算法求欧拉路径。为了满足条件,必须按顶点编号从小到大访问一个顶点的所有邻接点。
可以使用邻接矩阵或邻接表完成该题。
【题解代码】
解法1:邻接矩阵
#include<bits/stdc++.h>
using namespace std;
#define N 505
int edge[N][N], n, m, deg[N];//n:顶点数 m:边数 deg[i]:顶点i的度
stack<int> stk;
void dfs(int u)//Hierholzer算法
{for(int v = 1; v <= n; ++v){if(edge[u][v]){edge[u][v]--;edge[v][u]--;dfs(v);}}stk.push(u);
}
int main()
{int f, t, st = 1;//st:起点 cin >> m;for(int i = 1; i <= m; ++i){cin >> f >> t;n = max(n, max(f, t));edge[f][t]++;edge[t][f]++;deg[f]++;deg[t]++;}for(int v = 1; v <= n; ++v)//如果找到奇数度顶点,就从奇数度顶点出发,否则从1出发 {if(deg[v] % 2 == 1){st = v;break;}}dfs(st);while(stk.empty() == false){cout << stk.top() << endl;stk.pop();}return 0;
}
解法2:邻接表
#include<bits/stdc++.h>
using namespace std;
#define N 505
#define M 1050
struct Node
{int v, e;//v:顶点 e:边编号 Node(){}Node(int a, int b):v(a), e(b){}
};
int n, m, beg[N], deg[N];//n:顶点数 m:边数 deg[i]:顶点i的度 beg[i]:顶点i的邻接点从edge[i][beg[i]]开始
bool vis[M];//vis[i]:边i是否已访问过
vector<Node> g[N];
stack<int> stk;
bool cmp(Node a, Node b)
{return a.v < b.v;
}
void dfs(int u)//Hierholzer算法
{for(int &i = beg[u]; i < g[u].size(); ++i){int v = g[u][i].v, e = g[u][i].e;if(vis[e] == false){vis[e] = true;dfs(v);}}stk.push(u);
}
int main()
{int f, t, st = 1;//st:起点 cin >> m;for(int i = 1; i <= m; ++i){cin >> f >> t;n = max(n, max(f, t));g[f].push_back(Node(t, i));g[t].push_back(Node(f, i));deg[f]++;deg[t]++;}for(int v = 1; v <= n; ++v)sort(g[v].begin(), g[v].end(), cmp);for(int v = 1; v <= n; ++v){//如果找到奇数度顶点,就从奇数度顶点出发,否则从1出发 if(deg[v] % 2 == 1){st = v;break;}}dfs(st);while(stk.empty() == false){cout << stk.top() << endl;stk.pop();}return 0;
}
相关文章:
 | 洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences)
信息学奥赛一本通 1375:骑马修栅栏(fence) | 洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences
【题目链接】 ybt 1375:骑马修栅栏(fence) 洛谷 P2731 [USACO3.3]骑马修栅栏 Riding the Fences 【题目考点】 1. 图论:欧拉回路 欧拉回路存在的条件:图中所有顶点的度都是偶数欧拉路径存在的条件:图中只有两个度为奇数的顶点…...
Spring Boot 应用的打包和发布
1. 创建项目(example-fast) 基于 Spring Boot 创建一个 WEB 项目 example-fast。 2. 编译打包 2.1 采用 IDEA 集成的 Maven 环境来对 Spring Boot 项目编译打包,可谓是超级 easy 2.2 mvn 命令打包 # mvn clean 清理编译 # install 打包 #…...

linux:iptables (3) 命令行操练(一)
目录 1.命令行手册查缺补漏 2.开始练习,从最陌生的参数练习开启 2.1 --list-rules -S :打印链或所有链中的规则 2.2 --zero -Z 链或所有链中的零计数器 2.3 --policy -P 修改默认链的默认规则 2.4 --new -N 接下来练习添加和删除自定义链 1.命令行手册查缺补…...
 与synchronized(class) 有啥区别)
synchronized(this) 与synchronized(class) 有啥区别
前言 synchronized(this) 与 synchronized(class) 相同处:均对代码加锁,实现互斥性。synchronized(this) 与 synchronized(class) 区别:作用域不同。 synchronized (this) synchronized(this)使用的是对象锁。this为关键词,表示…...

BOSS直拒、失联招聘,消失的“金三银四”,失业的测试人出路在哪里?
裁员潮涌,经济严冬。最近很多测试人过得并不好,行业缩水对测试岗位影响很直接干脆,究其原因还是测试门槛在IT行业较低,同质化测试人员比较多。但实际上成为一位好测试却有着较高的门槛,一名优秀的测试应当对产品的深层…...

华为OD机试【密室逃生游戏】
密室逃生游戏 题目 小强增在参加《密室逃生》游戏,当前关卡要求找到符合给定 密码 K(升序的不重复小写字母组 成) 的箱子, 并给出箱子编号,箱子编号为 1~N 。 每个箱子中都有一个 字符串 s ,字符串由大写字…...

【Python学习笔记(六)】json解析模块的使用
json解析模块的使用 前言 json 是一种轻量级的数据交换格式,通过对象和数组的组合来表示数据。在 Python3 中可以使用 json 模块来对 json 数据进行编解码。 json 模块 是 Python 标准库模块,无需手动安装,可以直接导入 import json # 导入…...

《Spring系列》第3章 基于注解管理Bean
基于注解方式管理Bean 1.通过注解管理Bean 1) 基础注解 Component Service Controller Repository 2) 基于XML的注解扫描 a> 引入依赖 spring-aop-5.1.5.RELEASE.jarb> 开启组件扫描 最简单的开启注解 <context:component-scan base-package"com.jianan&q…...
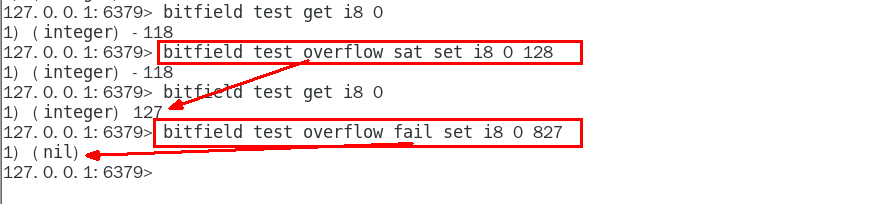
【Redis】十大数据类型(下篇)
文章目录redis位图(bitmap) --- 底子还是string基本命令图示setbit key offset value setbit 键 偏移位 只能零或者1getbit key offset 查看获取字符串长度 strlen统计key中包含1的个数 bitcount keybitop 统计两个比特key是否都为1技术落地:打卡签到,频…...
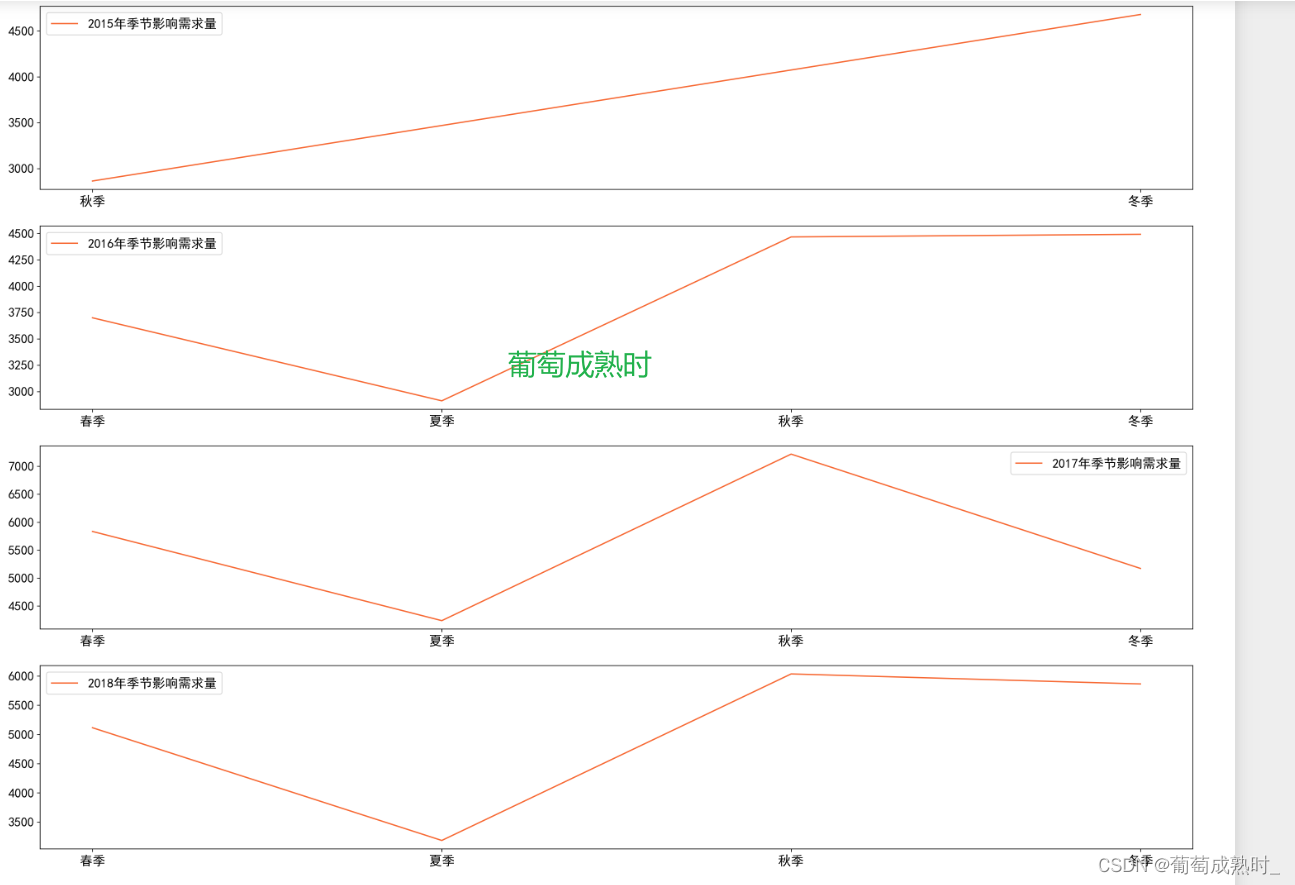
【第十一届“泰迪杯”数据挖掘挑战赛】B题产品订单的数据分析与需求预测“解题思路“”以及“代码分享”
【第十一届泰迪杯B题产品订单的数据分析与需求预测产品订单的数据分析与需求预测 】第一大问代码分享(后续更新LSTMinformer多元预测多变量模型) PS: 代码全写有注释,通俗易懂,包看懂!!!&…...

Python入门到高级【第一章】
预计更新第一章. Python 简介 Python 简介和历史Python 特点和优势安装 Python 第二章. 变量和数据类型 变量和标识符基本数据类型:数字、字符串、布尔值等字符串操作列表、元组和字典 第三章. 控制语句和函数 分支结构:if/else 语句循环结构&#…...

【泰凌微TLSR8258 zigbee】OTA升级操作方法
目录 程序启动模式多地址启动模式Bootloader 启动模式多地址启动模式 Flash 分布Bootloader 启动模式Flash分布模式OTA升级OTA初始化OTA ServerOTA ClientOTA升级固件生成程序启动模式 在介绍OTA升级操作方法前,我们先介绍一下程序的启动模式,以及不同启动模式的优缺点。 多…...

网络基础设施监控
在过去的几十年里,网络基础设施在规模和功能方面都变得复杂起来。不断增长的业务需求和不断增长的技术能力推动了这种快速增长,监控网络基础设施以确保其最佳性能和最大效率已成为任何希望成为行业领跑者的组织不可或缺的优先事项。 什么是网络基础设施…...

OPNET Modeler 例程——创建一个包交换网络
文章目录一、例程简介二、创建新的包格式三、创建新的链路模型四、创建中心交换节点模型五、创建中心交换节点的进程模型六、创建周边节点模型七、创建周边节点进程模块八、创建网络模型九、收集统计量十、配置并仿真总结一、例程简介 本例程将仿真一个简单的包交换网络&#…...

JSON 基础结构
什么是JSON JSON,说白了就是JavaScript用来处理数据的一种格式,这种格式非常简单易用。 JSON,大部分都是用来处理JavaScript和web服务器端之间的数据交换,把后台web服务器的数据传递到前台,然后使用JavaScript进行处…...

雷达基础知识
雷达频率划分 以下是按照频率和波长划分雷达频段的表格: 波段名称频率范围(GHz)波长范围(cm)应用领域VHF0.03 - 0.3100 - 10气象雷达、空管雷达、航空雷达UHF0.3 - 3100 - 10航空雷达、海上雷达、地面雷达、火控雷达…...
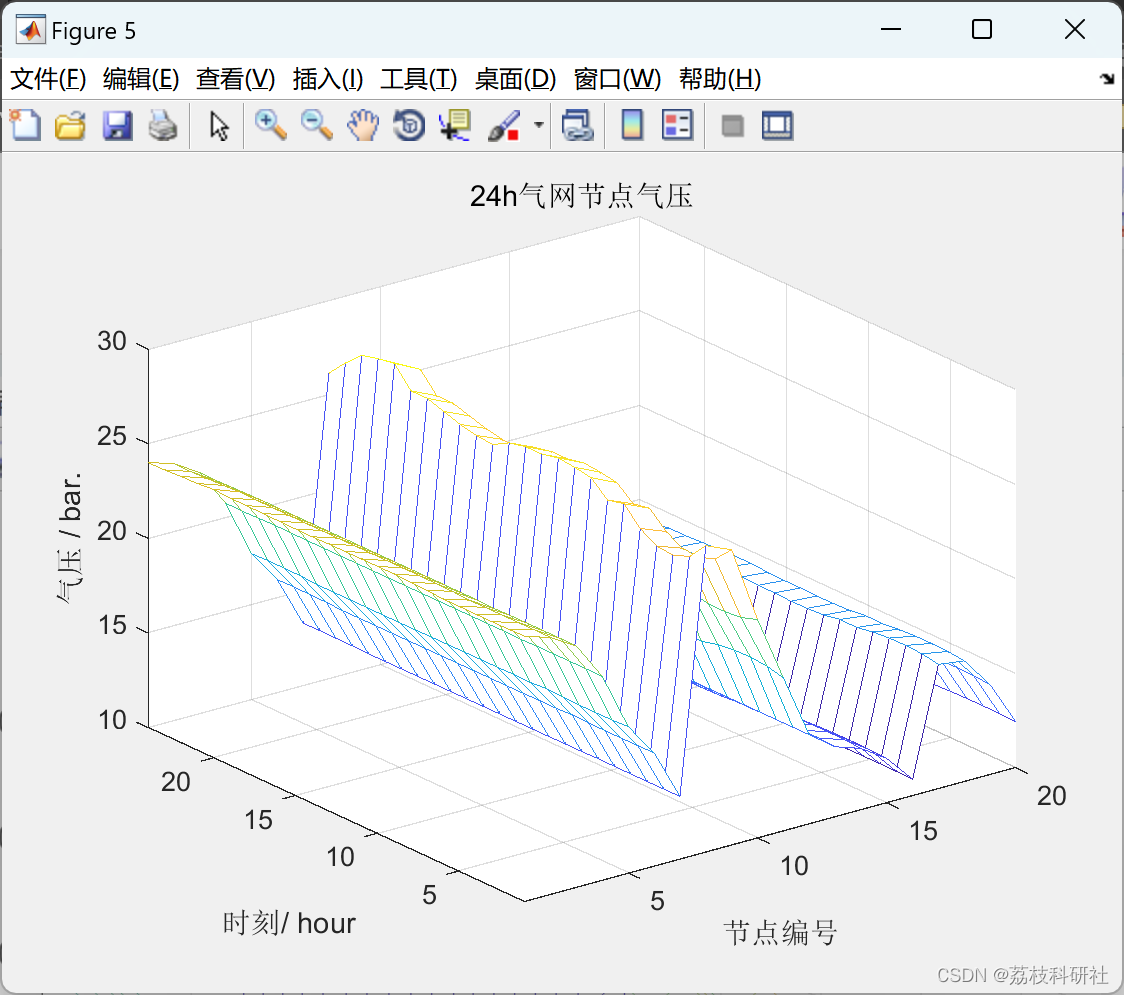
【二阶锥规划】考虑气电联合需求响应的气电综合能源配网系统协调优化运行【IEEE33节点】(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
qt 编译器 调试器
电脑版本:win10 64位 qt版本:based on Qt 5.14.0(msvc 2017, 32位) Qt Creator 4.11.0 qt安装包:qt-opensource-windows-x86-5.9.9.exe 安装过程一路next,安装完成后,默认使用的…...

低代码平台助力AIGC:让人工智能技术更加普及和高效
今年人工智能的风是吹了一波又一波,从ChatGPT到文心一言,短短四个多月的时间,GPT完成了从3.0、3.5到4.0的推新发布,一步步刷新了民众对于目前人工智能技术发展的认知底线,让人们直观地感受到了人工智能技术的蓬勃发展。…...

Qt中Model/View结构
Qt中Model/View结构 Model/View框架的核心思想是模型(数据)与视图(显示)相分离,模型对外提供标准接口存取数据,不关心数据如何显示,视图自定义数据的显示方式,不关心数据如何组织存…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
