当前位置： 首页 > news >正文

【计算机网络 - 基础问题】每日 3 题（二十五）

news 2026/2/8 21:15:33

✍个人博客：Pandaconda-CSDN博客
📣专栏地址：http://t.csdnimg.cn/fYaBd
📚专栏简介：在这个专栏中，我将会分享 C++ 面试中常见的面试题给大家~
❤️如果有收获的话，欢迎点赞👍收藏📁，您的支持就是我创作的最大动力💪
📝推荐参考地址：https://www.xiaolincoding.com/（这个大佬的专栏非常有用！）

73. TCP 三次握手过程是怎样的？

TCP 是面向连接的协议，所以使用 TCP 前必须先建立连接，而建立连接是通过三次握手来进行的。三次握手的过程如下图：

在这里插入图片描述

74. 如何在 Linux 系统中查看 TCP 状态？

TCP 的连接状态查看，在 Linux 可以通过 netstat -napt 命令查看。

在这里插入图片描述

75. 为什么是三次握手？不是两次、四次？

TCP 建立连接时，通过三次握手能防止历史连接的建立，能减少双方不必要的资源开销，能帮助双方同步初始化序列号。序列号能够保证数据包不重复、不丢弃和按序传输。

不使用「两次握手」和「四次握手」的原因：

  • 「两次握手」：无法防止历史连接的建立，会造成双方资源的浪费，也无法可靠的同步双方序列号；
  • 「四次握手」：三次握手就已经理论上最少可靠连接建立，所以不需要使用更多的通信次数。

相关文章：

【计算机网络 - 基础问题】每日 3 题（二十五）

✍个人博客：Pandaconda-CSDN博客 📣专栏地址：http://t.csdnimg.cn/fYaBd 📚专栏简介：在这个专栏中，我将会分享 C 面试中常见的面试题给大家~ ❤️如果有收获的话，欢迎点赞👍收藏&…...

编程日记 2024/9/27 23:09:54

【第十八章：Sentosa_DSML社区版-机器学习之协同过滤】

【第十八章：Sentosa_DSML社区版-机器学习之协同过滤】 1.算子介绍 协同过滤是推荐系统中常用的一种方法。该算法旨在填补用户-产品关联矩阵中缺少的项。在算法中，用户和产品都是通过一组少量的潜在因素描述，这些潜在因素可以用于预测用户-产…...

编程日记 2024/9/27 23:07:52

TDOA方法求二维坐标的MATLAB代码演示与讲解

引言 时间差定位（Time Difference of Arrival, TDOA）是一种用于确定信号源位置的技术，广泛应用于无线通信、声学定位等领域。通过测量信号到达多个接收器的时间差，可以计算出信号源的二维坐标。本文将通过MATLAB代码演示如何使用TDOA方法来求解二维坐标。 TDOA原理 TDOA…...

编程日记 2024/9/27 23:06:51

基于微信的原创音乐小程序的设计与实现+ssm论文源码调试讲解

第二章 开发工具及关键技术介绍 2.1 JAVA技术 Java主要采用CORBA技术和安全模型，可以在互联网应用的数据保护。它还提供了对EJB（Enterrise JavaBeans）的全面支持，java servlet AI，JS（java server ages&…...

编程日记 2024/9/27 23:05:50

基于大数据技术的颈椎病预防交流与数据分析及可视化系统

作者：计算机学姐 开发技术：SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等，“文末源码”。 专栏推荐：前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码 精品专栏：Java精选实战项目…...

编程日记 2024/9/27 23:02:46

Spring MVC中实现一个文件上传和下载功能

说到文件上传和下载，相信每个开发者都有或多或少的接触过文件上传的功能吧，文件上传和下载是我们在学习计算机网络应用常见的一个功能，主要涉及到用户和服务器之间的数据传输。 我们来对文件上传和下载功能的进行相关概述吧！ 文…...

编程日记 2024/9/27 23:01:45

Webpack 介绍

Webpack 介绍 Date: August 29, 2024 全文概要 Webpack概念： Webpack是一个静态的模块化的打包工具，可以为现代的 JavaSript 应用程序进行打包。 1-静态：Webpack可以将代码打包成最终的静态资源 2-模块化：webpack支持各种模块…...

编程日记 2024/9/27 23:00:42

在Linux实时监控某个应用是否运行，未运行，执行运行命令

1、shell脚本(每隔30秒检测一次) 脚本要注意的地方是：在Nodepad编辑的时候要使用Unix（LF）格式，避免在Linux无法执行命令 #!/bin/bash# RabbitMQ进程名称（可能需要根据你的安装进行调整） RABBITMQ_PROCE…...

编程日记 2024/9/27 22:59:41

Serilog文档翻译系列（六） - 可用的接收器、增强器、格式化输出

01、提供的接收器 Serilog 使用接收器将日志事件以各种格式写入存储。许多接收器由更广泛的 Serilog 社区开发和支持；可以通过在 NuGet 上搜索 serilog 标签找到。 02、增强器 日志事件可以通过多种方式增强属性。通过 NuGet 提供了一些预构建的增强器&#xff…...

编程日记 2024/9/27 22:57:39

傅里叶级数在机器人中的应用（动力学参数辨识）

B站首发！草履虫都能看懂的【傅里叶变换】讲解，清华大学李永乐老师教你如何理解傅里叶变换，辨清美颜和变声原理，！！_哔哩哔哩_bilibiliB站首发！草履虫都能看懂的【傅里叶变换】讲解，清…...

编程日记 2024/9/27 22:56:38

前端框架Vue、React、Angular、Svelte对比

在对比 React、Vue.js、Angular 和 Svelte 时，除了在高层次的特性上有显著差异，它们在核心设计理念和底层实现机制上也有明显的不同。为了清晰地理解这些框架，我们可以从以下几个方面来分析它们的核心不同点和底层不同点。 1. 框架类型和设计…...

编程日记 2024/9/27 22:55:37

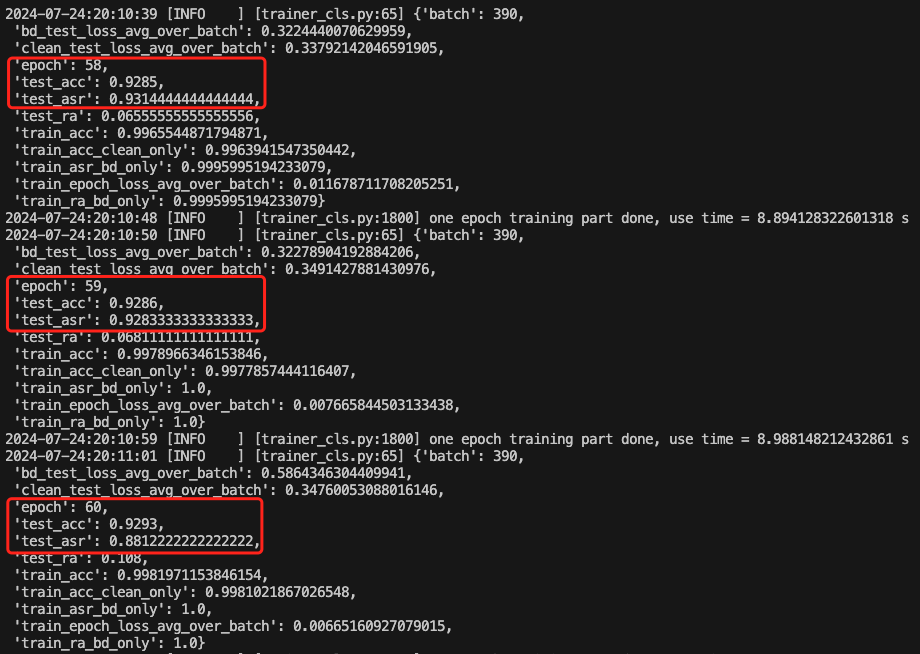
深度学习后门攻击分析与实现（二）

前言 在本系列的第一部分中，我们已经掌握了深度学习中的后门攻击的特点以及基础的攻击方式，现在我们在第二部分中首先来学习深度学习后门攻击在传统网络空间安全中的应用。然后再来分析与实现一些颇具特点的深度学习后门攻击方式。 深度学习与网络空间…...

编程日记 2024/9/27 22:54:36

boost 的lockfree 使用

boost 的lockfree 使用 // test.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。 // #define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <mutex> #include <memory> #include <condition_variable> #include <…...

编程日记 2024/9/27 22:52:35

基于Hexo个人博客界面优化

基于Hexo个人博客界面优化 怎么搭建个人博客 选择主题 经过多个对比&#xff0c;选择简单一点的的yilia 1.将主题文件下载解压到 你的博客目录的 themes下 下载yilia主题文件 2.改写配置 打开你的_config.yml #theme: landscape 这是原来的&#xff0c;改成下面这个 theme: yil…...

编程日记 2024/9/27 22:50:33

vue3+ts不能将类型“Timeout”分配给类型“null”不能将类型“Timeout”分配给类型number

在设置有setTimeout() 函数时&#xff0c;一般是需要进行清除计时器操作的&#xff1b; 常用的做法是定义一个全局变量timer&#xff0c;在onMounted或者有需要的地方进行赋值&#xff0c;在onBeforeUnmount进行clear&#xff0c;一般在定义timer变量时&#xff0c;使用 numbe…...

编程日记 2024/9/27 22:49:32

如何给多台Linux机器设置时间同步

文章目录 1&#xff0c;使用chrony时间同步服务1.1 修改chrony配置文件 2&#xff0c;使用ntpdate服务 1&#xff0c;使用chrony时间同步服务 Centos7默认已安装&#xff0c;另外基于centos7的统信OS&#xff0c;中科OS也会默认安装这个。如果你机器上没有这个服务&#xff0c…...

编程日记 2024/9/27 22:48:31

忘写return有什么现象？

使用C语言&#xff0c;一直觉得没有return无所谓&#xff0c;直到被制裁。。 参考&#xff1a; 非void函数缺失返回值导致crash或结果异常的分析 - 知乎 (zhihu.com) 可以分析出&#xff1a; 没有写return 的话&#xff0c;eax的内容是在预期之外的。 例如更新参考内容的解…...

编程日记 2024/9/27 22:47:30

大数据新视界 --大数据大厂之 Druid 实时数据分析平台在大数据中的应用

&#x1f496;&#x1f496;&#x1f496;亲爱的朋友们&#xff0c;热烈欢迎你们来到 青云交的博客&#xff01;能与你们在此邂逅&#xff0c;我满心欢喜&#xff0c;深感无比荣幸。在这个瞬息万变的时代&#xff0c;我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

编程日记 2024/9/27 22:46:29

MySQL --基本查询（下）

文章目录 3.Update3.1将孙悟空同学的数学成绩变更为 80 分3.2将曹孟德同学的数学成绩变更为 60 分&#xff0c;语文成绩变更为 70 分3.3将总成绩倒数前三的 3 位同学的数学成绩加上 30 分3.4将所有同学的语文成绩更新为原来的 2 倍 4.Delete4.1删除数据4.1.1删除孙悟空同学的考…...

编程日记 2024/9/27 22:42:08

vue3实现自定义主题色切换功能

目录 1.添加theme样式文件2.引入样式文件3.使用变量设置css样式4.设置主题样式5.切换方法 1.添加theme样式文件 文件内容如下&#xff1a; html[data-theme"light"]{--text-color: #000000;/* 写需要切换的样式 */ } html[data-theme"dark"]{--text-color…...

编程日记 2024/9/27 22:41:07

day52 ResNet18 CBAM

在深度学习的旅程中&#xff0c;我们不断探索如何提升模型的性能。今天&#xff0c;我将分享我在 ResNet18 模型中插入 CBAM&#xff08;Convolutional Block Attention Module&#xff09;模块&#xff0c;并采用分阶段微调策略的实践过程。通过这个过程&#xff0c;我不仅提升…...

编程新知 2025/11/9 1:27:18

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达

先前我们总结了浏览器选区模型的交互策略&#xff0c;并且实现了基本的选区操作&#xff0c;还调研了自绘选区的实现。那么相对的&#xff0c;我们还需要设计编辑器的选区表达&#xff0c;也可以称为模型选区。编辑器中应用变更时的操作范围&#xff0c;就是以模型选区为基准来…...

编程新知 2026/1/16 16:34:26

centos 7 部署awstats 网站访问检测

一、基础环境准备&#xff08;两种安装方式都要做&#xff09; bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats&#xff0…...

编程新知 2026/1/23 8:33:56

【Go语言基础【12】】指针：声明、取地址、解引用

文章目录 零、概述&#xff1a;指针 vs. 引用&#xff08;类比其他语言&#xff09;一、指针基础概念二、指针声明与初始化三、指针操作符1. &&#xff1a;取地址&#xff08;拿到内存地址&#xff09;2. *&#xff1a;解引用&#xff08;拿到值&#xff09; 四、空指针&am…...

编程新知 2025/6/21 2:18:57

MySQL 8.0 事务全面讲解

以下是一个结合两次回答的 MySQL 8.0 事务全面讲解&#xff0c;涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容&#xff0c;并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念&#xff08;ACID&#xff09; 事务是…...

编程新知 2025/9/19 22:12:36

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案

目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后&#xff0c;迭代器会失效&#xff0c;因为顺序迭代器在内存中是连续存储的&#xff0c;元素删除后&#xff0c;后续元素会前移。 但一些场景中&#xff0c;我们又需要在执行删除操作…...

编程新知 2025/9/30 8:10:20

Proxmox Mail Gateway安装指南：从零开始配置高效邮件过滤系统

&#x1f49d;&#x1f49d;&#x1f49d;欢迎莅临我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐&#xff1a;「storms…...

编程新知 2026/1/17 14:57:41

在 Spring Boot 中使用 JSP

jsp&#xff1f; 好多年没用了。重新整一下 还费了点时间&#xff0c;记录一下。 项目结构&#xff1a; pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

编程新知 2026/2/4 11:39:13

通过MicroSip配置自己的freeswitch服务器进行调试记录

之前用docker安装的freeswitch的&#xff0c;启动是正常的&#xff0c; 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

编程新知 2026/2/6 14:23:05

Linux中《基础IO》详细介绍

目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改&#xff0c;实现简单cat命令 输出信息到显示器&#xff0c;你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

编程新知 2026/2/3 4:42:54