算法训练第四十四天|完全背包理论 、518. 零钱兑换 II、377. 组合总和 Ⅳ
第九章 动态规划part06
- 完全背包理论基础
- 完全背包
- C++测试代码
- 总结
- 518. 零钱兑换 II
- 题目描述
- 思路
- 总结
- 377. 组合总和 Ⅳ
- 题目描述
- 思路
- 总结
完全背包理论基础
参考:https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html
完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
同样leetcode上没有纯完全背包问题,都是需要完全背包的各种应用,需要转化成完全背包问题,所以我这里还是以纯完全背包问题进行讲解理论和原理。
在下面的讲解中,我依然举这个例子:
背包最大重量为4。
物品为:

每件商品都有无限个!
问背包能背的物品最大价值是多少?
01背包和完全背包唯一不同就是体现在遍历顺序上,所以本文就不去做动规五部曲了,我们直接针对遍历顺序经行分析!
首先在回顾一下01背包的核心代码
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
dp状态图如下:
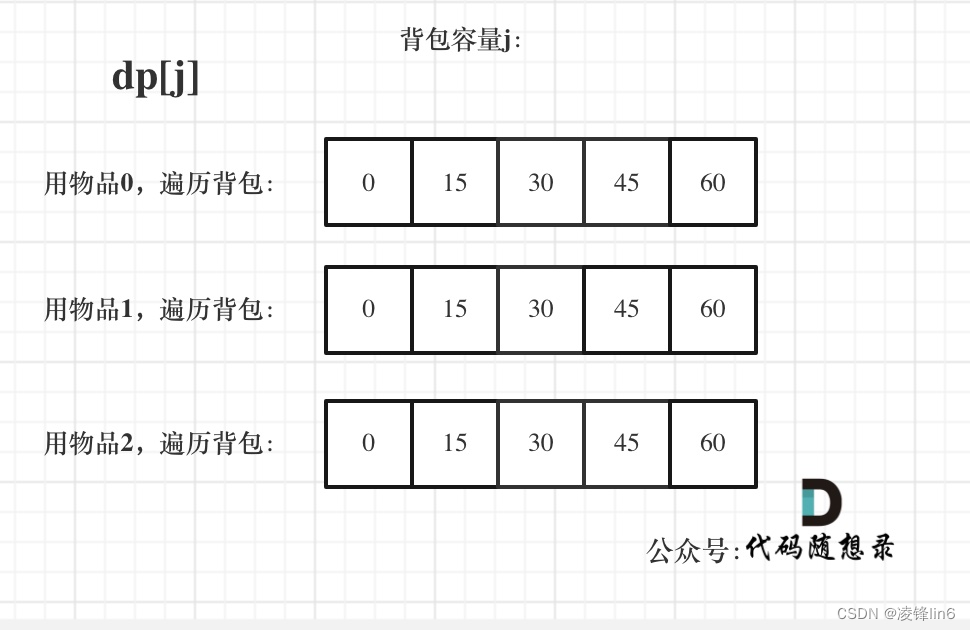
其实还有一个很重要的问题,为什么遍历物品在外层循环,遍历背包容量在内层循环?
这个问题很多题解关于这里都是轻描淡写就略过了,大家都默认 遍历物品在外层,遍历背包容量在内层,好像本应该如此一样,那么为什么呢?
难道就不能遍历背包容量在外层,遍历物品在内层?
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
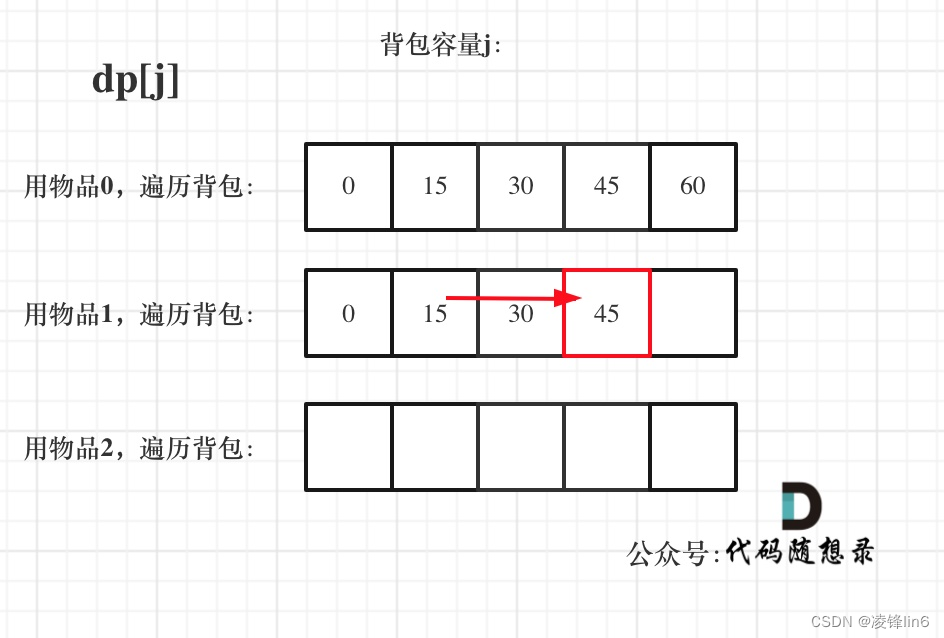
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
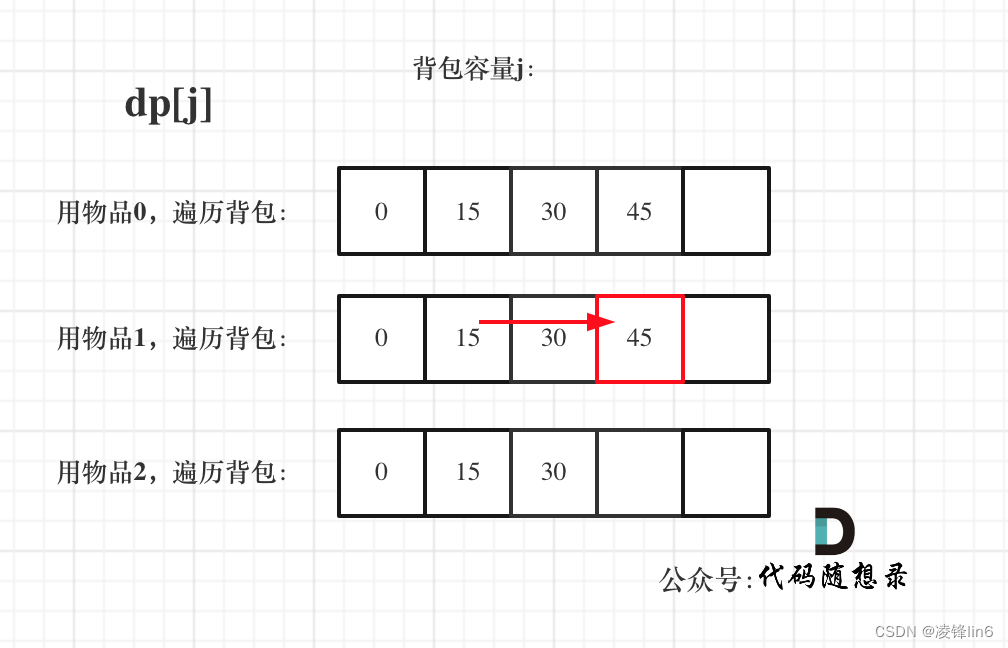
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值(这个值就是下标j之前所对应的dp[j])。
先遍历背包在遍历物品,代码如下:
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量for(int i = 0; i < weight.size(); i++) { // 遍历物品if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}cout << endl;
}
C++测试代码
完整的C++测试代码如下:
// 先遍历物品,在遍历背包
void test_CompletePack() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}
int main() {test_CompletePack();
}
// 先遍历背包,再遍历物品
void test_CompletePack() {vector<int> weight = {1, 3, 4};vector<int> value = {15, 20, 30};int bagWeight = 4;vector<int> dp(bagWeight + 1, 0);for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量for(int i = 0; i < weight.size(); i++) { // 遍历物品if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}
int main() {test_CompletePack();
}
总结
细心的同学可能发现,全文我说的都是对于纯完全背包问题,其for循环的先后循环是可以颠倒的!
但如果题目稍稍有点变化,就会体现在遍历顺序上。
如果问装满背包有几种方式的话? 那么两个for循环的先后顺序就有很大区别了,而leetcode上的题目都是这种稍有变化的类型。
这个区别,我将在后面讲解具体leetcode题目中给大家介绍,因为这块如果不结合具题目,单纯的介绍原理估计很多同学会越看越懵!
别急,下一篇就是了!哈哈
最后,又可以出一道面试题了,就是纯完全背包,要求先用二维dp数组实现,然后再用一维dp数组实现,最后在问,两个for循环的先后是否可以颠倒?为什么? 这个简单的完全背包问题,估计就可以难住不少候选人了。
518. 零钱兑换 II
题目链接:518. 零钱兑换 II
参考:https://programmercarl.com/0518.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2II.html
题目描述
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
- 输入: amount = 5, coins = [1, 2, 5]
- 输出: 4
解释: 有四种方式可以凑成总金额:
- 5=5
- 5=2+2+1
- 5=2+1+1+1
- 5=1+1+1+1+1
示例 2:
- 输入: amount = 3, coins = [2]
- 输出: 0
- 解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
- 输入: amount = 10, coins = [10]
- 输出: 1
注意,你可以假设:
- 0 <= amount (总金额) <= 5000
- 1 <= coin (硬币面额) <= 5000
- 硬币种类不超过 500 种
- 结果符合 32 位符号整数
思路
这是一道典型的背包问题,一看到钱币数量不限,就知道这是一个完全背包。
但本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
注意题目描述中是凑成总金额的硬币组合数,为什么强调是组合数呢?
例如示例一:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
如果问的是排列数,那么上面就是两种排列了。
组合不强调元素之间的顺序,排列强调元素之间的顺序。 其实这一点我们在讲解回溯算法专题的时候就讲过了哈。
那我为什么要介绍这些呢,因为这和下文讲解遍历顺序息息相关!
回归本题,动规五步曲来分析如下:
- 确定dp数组以及下标的含义
dp[j]:凑成总金额j的货币组合数为dp[j]
- 确定递推公式
dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加。
所以递推公式:dp[j] += dp[j - coins[i]];
这个递推公式大家应该不陌生了,我在讲解01背包题目的时候在这篇494. 目标和 中就讲解了,求装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];
- dp数组如何初始化
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。
那么 dp[0] = 1 有没有含义,其实既可以说 凑成总金额0的货币组合数为1,也可以说 凑成总金额0的货币组合数为0,好像都没有毛病。
但题目描述中,也没明确说 amount = 0 的情况,结果应该是多少。
这里我认为题目描述还是要说明一下,因为后台测试数据是默认,amount = 0 的情况,组合数为1的。
下标非0的dp[j]初始化为0,这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]
dp[0]=1还说明了一种情况:如果正好选了coins[i]后,也就是j-coins[i] == 0的情况表示这个硬币刚好能选,此时dp[0]为1表示只选coins[i]存在这样的一种选法。
- 确定遍历顺序
本题中我们是外层for循环遍历物品(钱币),内层for遍历背包(金钱总额),还是外层for遍历背包(金钱总额),内层for循环遍历物品(钱币)呢?
完全背包的两个for循环的先后顺序都是可以的。
但本题就不行了!
因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
那么本题,两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}
假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}
背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
可能这里很多同学还不是很理解,建议动手把这两种方案的dp数组数值变化打印出来,对比看一看!(实践出真知)
- 举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
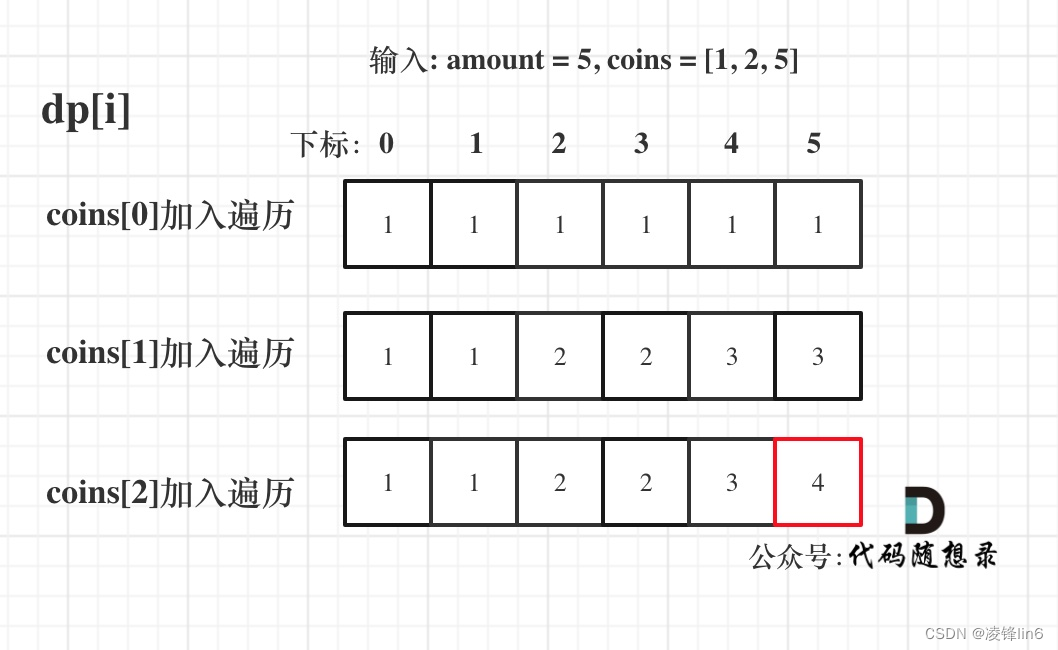
最后红色框dp[amount]为最终结果。
以上分析完毕,C++代码如下:
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包dp[j] += dp[j - coins[i]];}}return dp[amount];}
};
总结
本题的递推公式,其实我们在494. 目标和 中就已经讲过了,而难点在于遍历顺序!
在求装满背包有几种方案的时候,认清遍历顺序是非常关键的。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
可能说到排列数录友们已经有点懵了,后面Carl还会安排求排列数的题目,到时候在对比一下,大家就会发现神奇所在!
377. 组合总和 Ⅳ
题目链接:377. 组合总和 Ⅳ
参考:https://programmercarl.com/0377.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C%E2%85%A3.html
题目描述
难度:中等
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
- nums = [1, 2, 3]
- target = 4
- 所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
思路
本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列!
弄清什么是组合,什么是排列很重要。
组合不强调顺序,(1,5)和(5,1)是同一个组合。
排列强调顺序,(1,5)和(5,1)是两个不同的排列。
大家在公众号里学习回溯算法专题的时候,一定做过这两道题目回溯算法:39.组合总和和回溯算法:40.组合总和II 会感觉这两题和本题很像!
但其本质是本题求的是排列总和,而且仅仅是求排列总和的个数,并不是把所有的排列都列出来。
如果本题要把排列都列出来的话,只能使用回溯算法爆搜。
动规五部曲分析如下:
- 确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
- 确定递推公式
dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导出来。
因为只要得到nums[j],排列个数dp[i - nums[j]],就是dp[i]的一部分。
求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
- dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
至于dp[0] = 1 有没有意义呢?
其实没有意义,所以我也不去强行解释它的意义了,因为题目中也说了:给定目标值是正整数! 所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
至于非0下标的dp[i]应该初始为多少呢?
初始化为0,这样才不会影响dp[i]累加所有的dp[i - nums[j]]。
- 确定遍历顺序
个数可以不限使用,说明这是一个完全背包。
得到的集合是排列,说明需要考虑元素之间的顺序。
本题要求的是排列,那么这个for循环嵌套的顺序可以有说法了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
- 举例来推导dp数组
我们再来用示例中的例子推导一下:

如果代码运行处的结果不是想要的结果,就把dp[i]都打出来,看看和我们推导的一不一样。
以上分析完毕,C++代码如下:
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);dp[0] = 1;for (int i = 0; i <= target; i++) { // 遍历背包for (int j = 0; j < nums.size(); j++) { // 遍历物品if (i - nums[j] >= 0 && dp[i] < INT_MAX - dp[i - nums[j]]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
};
C++测试用例有两个数相加超过int的数据,所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。
总结
求装满背包有几种方法,递归公式都是一样的,没有什么差别,但关键在于遍历顺序!
本题与动态规划:518.零钱兑换II就是一个鲜明的对比,一个是求排列,一个是求组合,遍历顺序完全不同。
如果对遍历顺序没有深度理解的话,做这种完全背包的题目会很懵逼,即使题目刷过了可能也不太清楚具体是怎么过的。
相关文章:

算法训练第四十四天|完全背包理论 、518. 零钱兑换 II、377. 组合总和 Ⅳ
第九章 动态规划part06完全背包理论基础完全背包C测试代码总结518. 零钱兑换 II题目描述思路总结377. 组合总和 Ⅳ题目描述思路总结完全背包理论基础 参考:https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%…...
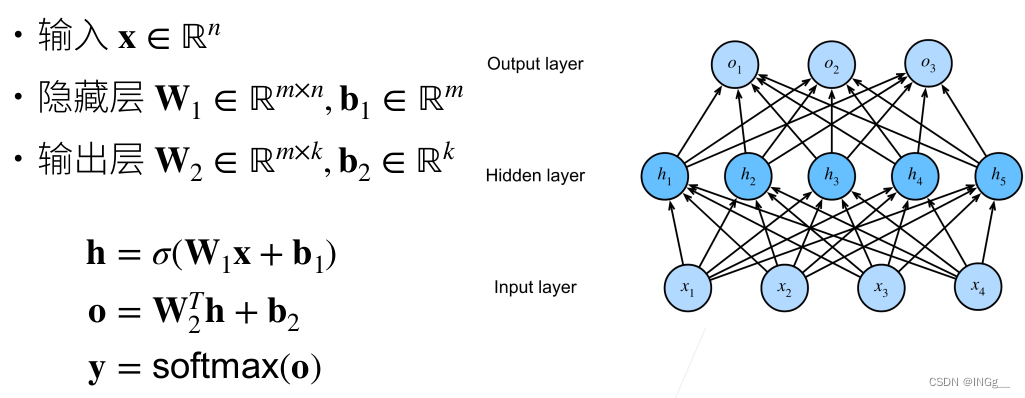
0x06多层感知机
感知机 感知机形象的来看就是我们接触过的一个只有两个部分组成(输出和输入)组成的最简单的神经网络之一。 给定输入x,权重w和偏移b以及一个感知函数,感知机就能输出: 这个函数可以形象的用作二分类问题,…...
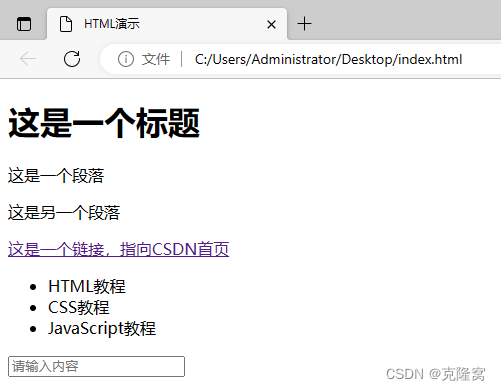
HTML是什么?HTML简介
HTML 英文全称是 Hyper Text Markup Language,中文译为“超文本标记语言”,专门用来设计和编辑网页。 使用 HTML 编写的文件称为“HTML 文档”,一般后缀为.html(也可以使用.htm,不过比较少见)。HTML 文档是…...

Linux定时服务
目录 1、定时器操作 2.cron表达式的语法规则 参考链接 1、定时器操作 sudo crontab -e 【选择2】 进入进行配置【需要按下 i 】 #sh /home/xx/crontabsh/test.sh的意思是,让sh解释器调用test.sh脚本,到达定时执行任务的效果 # 每一分钟执行一次 *…...

sgi_stl源码学习,官方文档3.2.3String package字符串封装,未完待续
https://www.boost.org/sgi/stl/character_traits.html char_traits<char> char_traits<wchar_t>traits翻译为特征、特性类,一般是指某种类型的特性类应该提供的一组接口、类型定义。 web页面描述了一些接口要求。感觉没有什么特别的。直接看代码吧 c…...
:基础知识)
从JavaScript到Java(一):基础知识
Hello World Java和JavaScript虽然有不同的特点,但在一些概念和知识点上是相似的。本文从JavaScript开发者的角度出发,帮助你理解Java基础知识(反过来也行)。 // 解释型 console.log("Hello, World!");// 编译型 pub…...

Android编舞者类Choreographer小结
Android编舞者类Choreographer小结 作用 编舞者类的作用主要是控制绘制节奏,用于发起一次vsync垂直同步信号的监听,当垂直同步信号来的时候会回调注册的Runnable或者FramCallback Choreographer对象获取 Choreographer对象是通过它的getInstance方法…...

大专升本科难度大吗 需要考哪些科目
大专学历可以通过自考和成考提升学历到本科,自考的考试科目有12-16门左右,考试内容不难,但是考试周期长,需要考生通过所有课程才能申请毕业。成考专升本考试科目有政治,外语和专业课,考试内容简单ÿ…...

考研复试-英语问答+解答
每个问题2~3min 一、 1.考官问问题,没听明白 I’m sorry, I didn’t hear that clearly. May I ask you to repeat it, please? Sorry, I have no clear idea about this question for now, but I will think about it later. And if possible, I want to discuss …...
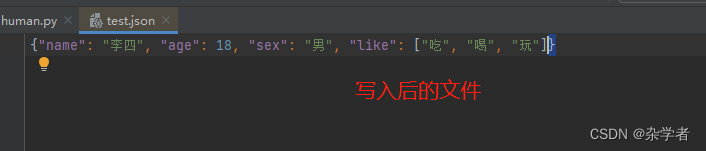
python 文件相关的操作 常用函数(读文件、写文件、文件的追加内容、修改文件内容、复制文件、按行读取文件、with open) json文件的读取
常用函数:open(打开文件),read(读文件到程序中),write(写程序中的变量到文件),close(关闭文件) 示例1:读文件(…...

python 系列 06 -生成及解析二维码
0 说明 二维码不止一种,本文介绍最常见的QR二维码。由于不能发二维码截图,所以所有的执行结果都隐去了。完整版本可以移步到此查看:https://vblogs.cn/momo1938/article?id0407576070659864 1 安装包 python 可以使用qrcode来生成二维码&…...

2023第二届中国绿色钢铁国际峰会
会议背景 钢铁是当今世界上最常用的金属,普遍应用于世界各国基础设施建设与机械、汽车、飞机、船舶、家电等产品的生产制造中。但是,随着各国政府与行业净零排放目标的确立,钢铁行业的减排降碳也成为了关注焦点。据世界钢铁协会称,…...
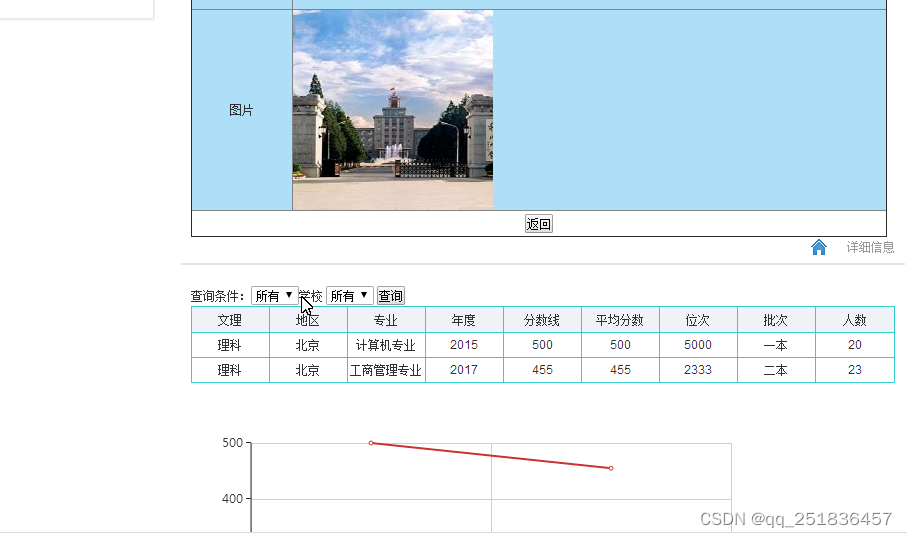
java 高考志愿填报系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目
一、源码特点 java 高考志愿填报系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0…...
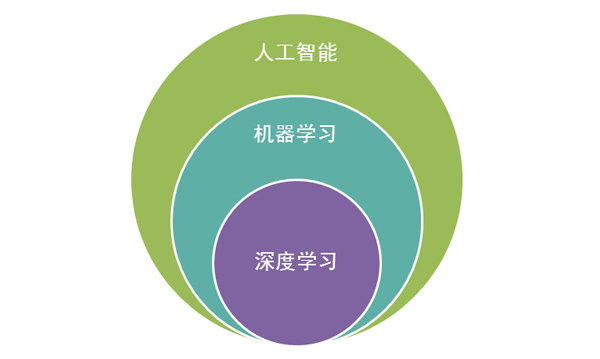
机器学习 vs 深度学习:了解两者的异同
在人工智能领域中,机器学习和深度学习是两个重要的概念。尽管它们都可以用于处理复杂的数据和任务,但它们在其基本原理、算法和应用方面有着显著的不同之处。在本文中,我们将详细介绍机器学习和深度学习的定义、原理、算法和应用,…...
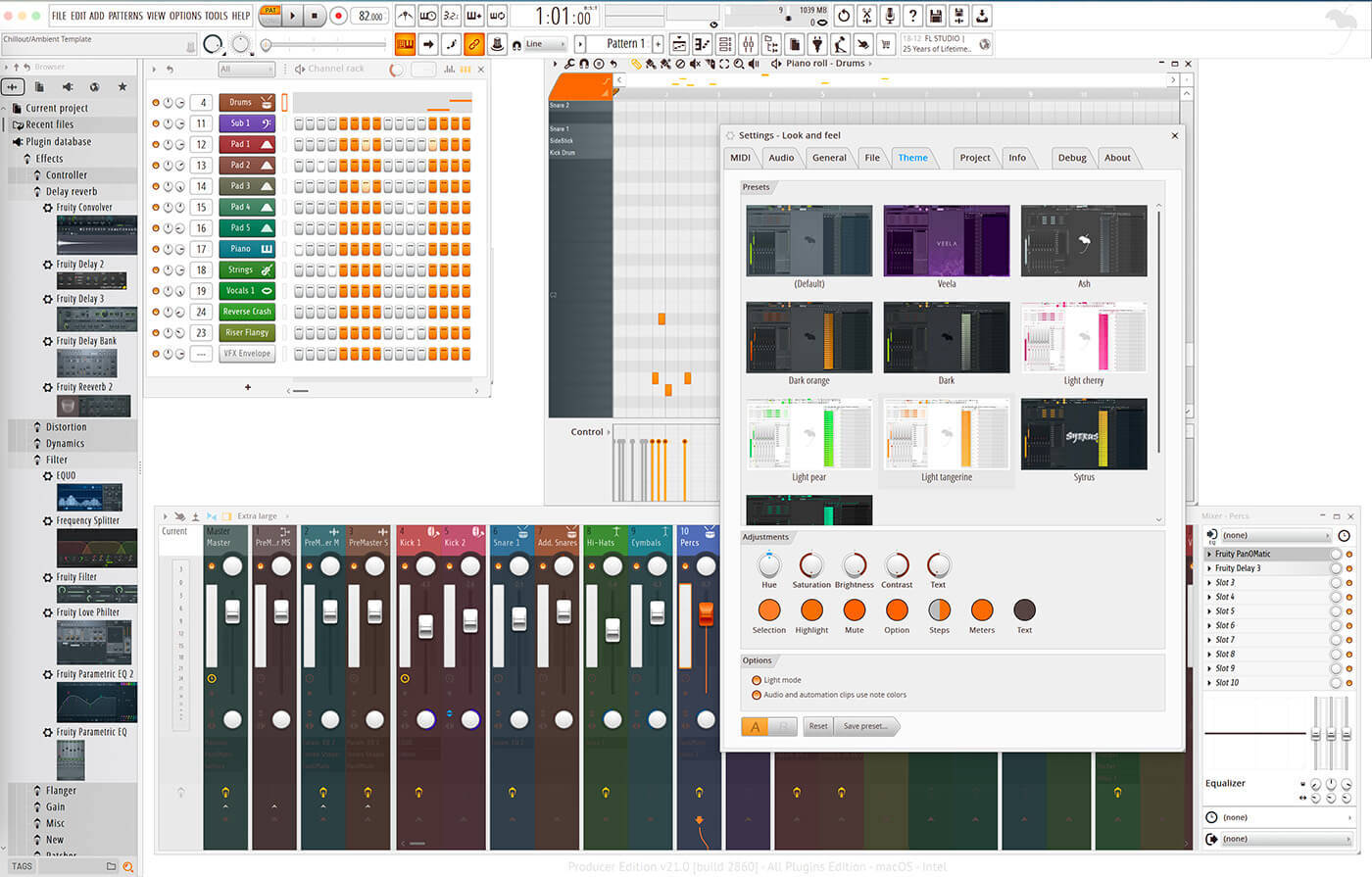
流行的 DAW编曲软件FL Studio 21 有什么新功能?
FL Studio 21 对流行的 DAW 和音乐制作软件进行了多项更新。最重要的变化包括:更快、更精确的音频包络和带有自动交叉推子的增益控制;一个能够标记、制作自定义颜色的标签和访问在线内容的新浏览器,以及一个带有可视化和擦除功能的内嵌音频播…...
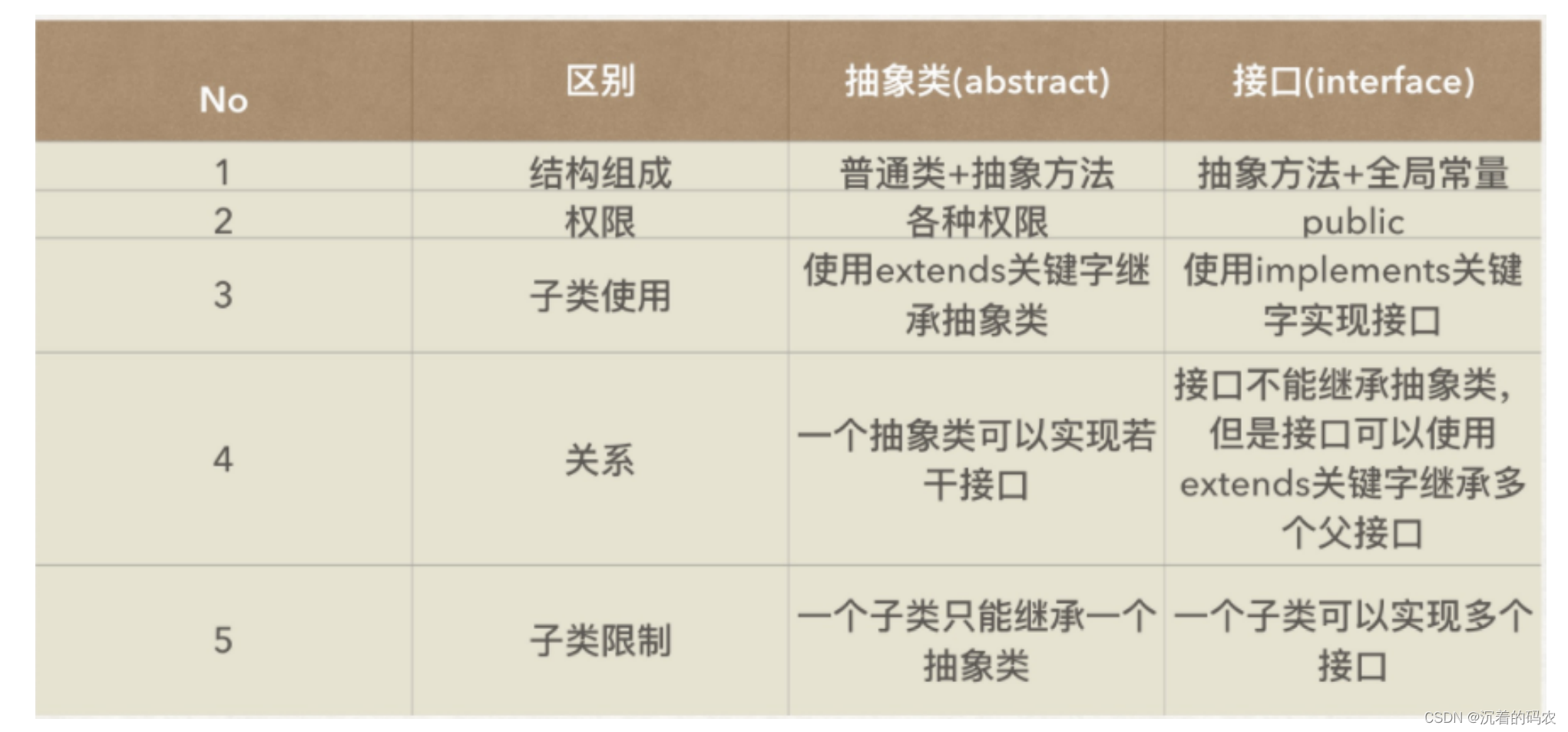
【Java】抽象类和接口
抽象类和接口抽象类抽象类的概念抽象类语法抽象类的注意事项抽象类的作用接口接口的概念语法规则接口使用接口注意实现多个接口接口间的继承接口使用实例给对象数组排序Clonable 接口和深拷贝浅拷贝深拷贝抽象类和接口的区别抽象类 抽象类的概念 在面向对象的概念中ÿ…...
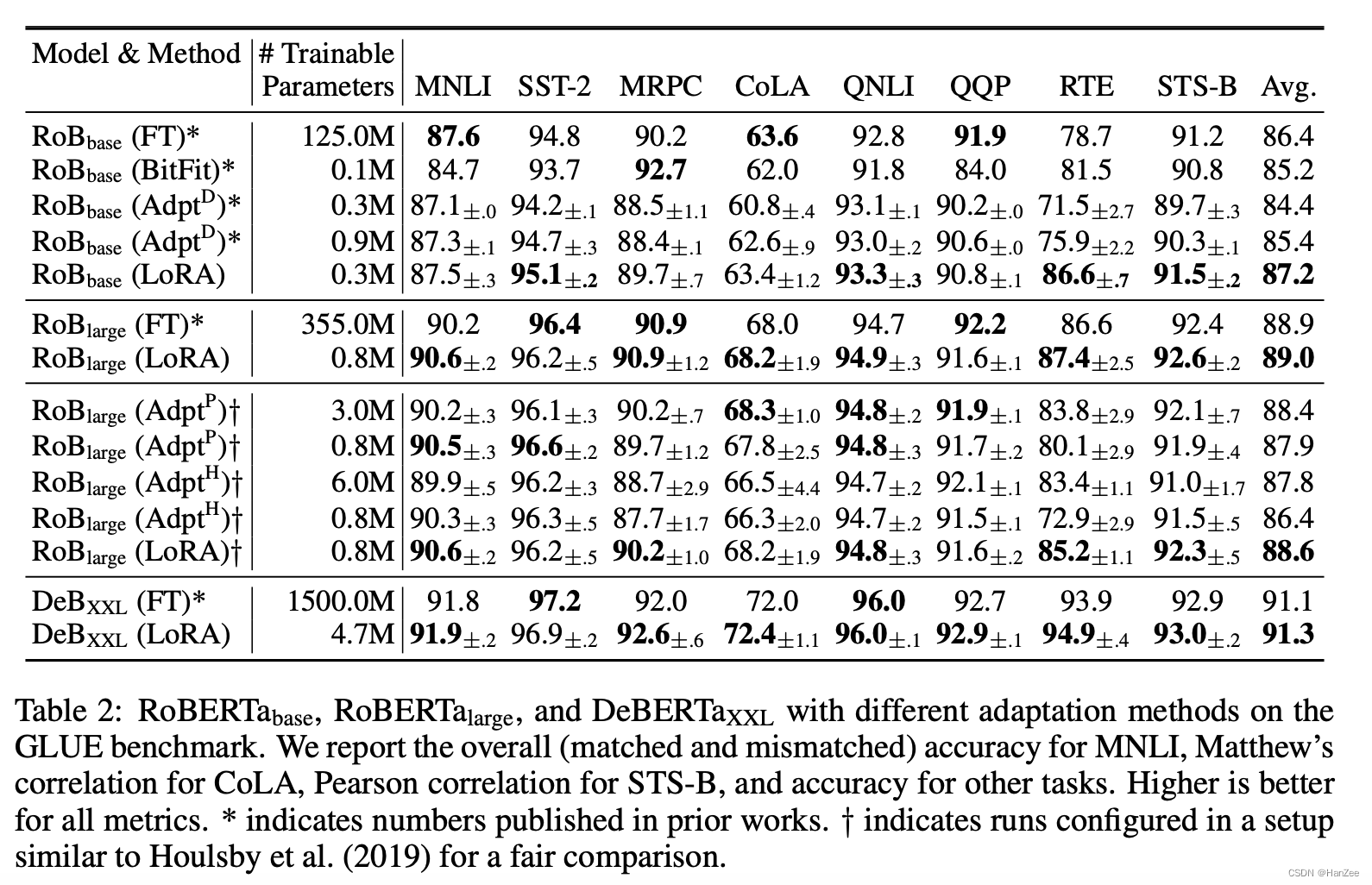
Lora:Low-Rank Adapation of Large Language models
Lora:Low-Rank Adapation of Large Language modelsIntroductionMethodExperiment代码Introduction 这篇论文最初与21.06上传与arXiv,作者指出在当时,NLP的一个重要范式是先训练一个通用领域的模型然后在通过微调适应不同的领域与数据&#…...
洛谷-P8466 [Aya Round 1 A] 幻想乡扑克游戏
题目:P8466 [Aya Round 1 A] 幻想乡扑克游戏 题目描述: 题目描述 斗地主是一种使用 �A 到 �K 加上大小王的共 5454 张扑克牌来进行的游戏,其中大小王各一张,其它数码牌各四张。在斗地主中,牌的…...

HBase性能优化方法总结
1. 表的设计 1.1 Pre-Creating Regions 默认情况下,在创建HBase表的时候会自动创建一个region分区,当导入数据的时候,所有的HBase客户端都向这一个region写数据,直到这个region足够大了才进行切分。一种可以加快批量写入速度的方…...
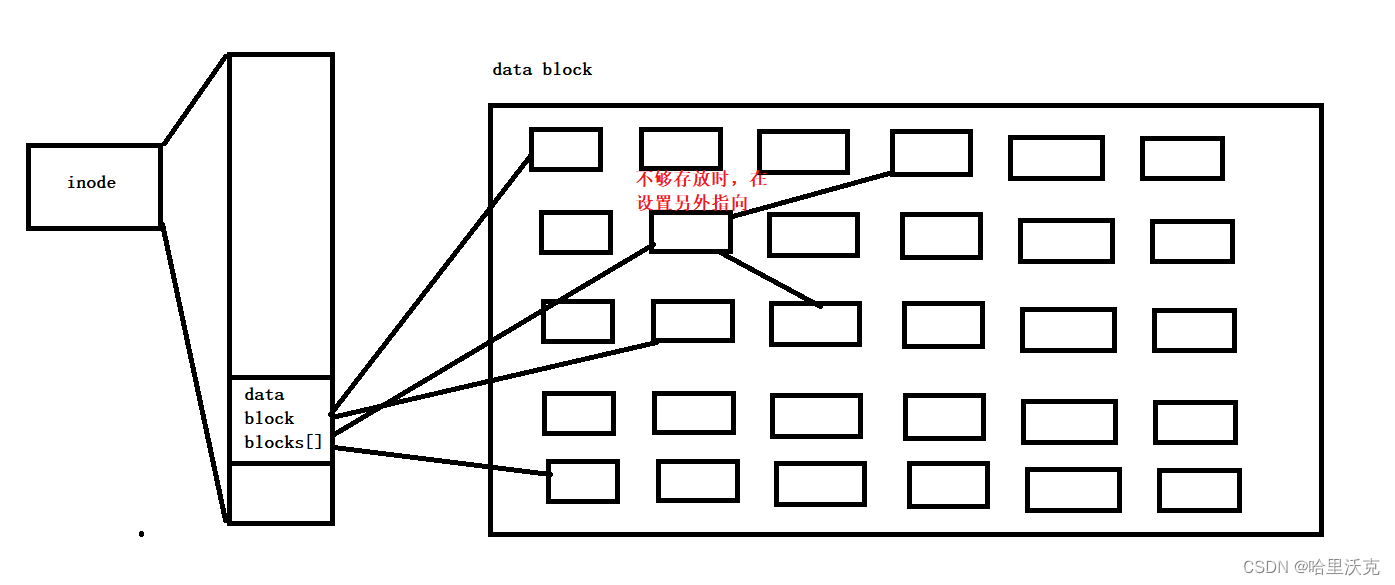
Linux基础内容(16)—— 文件系统
Linux基础内容(15)—— 缓冲区https://blog.csdn.net/m0_63488627/article/details/129824563?spm1001.2014.3001.5501 目录 1.基础知识 2.磁盘的存储原理 1.物理结构 2.存储结构 3.逻辑结构 1.基础知识 之前介绍的全是进程打开的文件是如何执行…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
