Web 3.0 介绍
Web 3.0 是互联网的下一代发展阶段,通常被称为去中心化的网络。它与目前的 Web 2.0(以社交媒体、云计算和中心化平台为主导)不同,强调用户对数据和内容的更多掌控,依靠区块链、加密货币、去中心化应用(DApps)等技术来实现。这些特性将带来更透明、安全和自主的互联网体验。
Web 3.0 的核心特性:
-
去中心化:
- 与 Web 2.0 中的数据集中在大公司服务器上不同,Web 3.0 使用区块链等去中心化技术,将数据分布式存储。这意味着用户不再依赖于少数公司(如 Google、Facebook)来获取和控制信息。
-
数据所有权:
- 在 Web 3.0 中,用户对他们的数据拥有完全控制权,数据存储在分布式网络中,用户可以决定是否分享数据,如何使用,并通过智能合约自动化处理授权。
-
信任与安全:
- 区块链技术确保数据不可篡改,所有交易、信息交互都通过共识机制验证,降低了数据泄露和网络攻击的风险。去中心化身份(DID)让用户可以通过加密密钥来管理自己的数字身份,避免依赖于中央机构。
-
智能合约与自动化:
- Web 3.0 广泛使用智能合约,这是一种自动执行的程序,当满足预定条件时,合约会自动执行,无需第三方干预。智能合约广泛应用于去中心化金融(DeFi)、去中心化自治组织(DAO)等场景。
-
无信任系统:
- Web 3.0 系统基于密码学技术实现,用户无需依赖信任中心化的中介机构(如银行或平台),而是通过技术本身保证安全性与透明度。
-
开放性:
- Web 3.0 通过去中心化协议构建,开发者和用户可以自由参与,不受中心化平台的限制。任何人都可以开发、发布或参与 Web 3.0 应用。
-
语义网:
- Web 3.0 引入了语义网(Semantic Web)的概念,通过增强机器理解能力,使得互联网可以处理更复杂的查询,理解数据之间的关系,从而提供更精准的搜索和个性化推荐。
Web 3.0 的应用场景:
-
去中心化金融(DeFi):
- Web 3.0 支持去中心化金融应用,通过区块链技术提供金融服务,如借贷、支付、交易等,用户不再需要通过传统银行和中介,而是通过智能合约直接参与。
-
去中心化应用(DApps):
- DApps 是运行在去中心化网络上的应用程序,通常由区块链作为基础设施,不受传统服务器的控制。它们可以应用于游戏、社交媒体、内容分发等领域。
-
去中心化自治组织(DAO):
- DAO 是一种由智能合约驱动的组织,管理权由参与者持有的代币决定,所有决策通过投票来达成,无需中央领导机构。
-
NFT 和数字资产:
- Web 3.0 支持不可替代代币(NFT)和其他数字资产的创建和交易,这为艺术品、音乐、虚拟地产等数字内容的所有权和分发提供了全新的方式。
Web 3.0 的挑战:
- 技术门槛:尽管区块链技术在 Web 3.0 中至关重要,但其学习和开发门槛较高,导致广泛普及需要时间。
- 可扩展性:去中心化网络的效率可能比中心化网络低,尤其是在处理大量数据和交易时。
- 法规与合规:由于 Web 3.0 的去中心化特性,监管面临挑战,如何平衡去中心化与合法合规是重要议题。
总结:
Web 3.0 是互联网的未来发展方向,通过去中心化、用户自主权、智能合约等特性,重新定义了网络的结构和运作方式。这不仅改变了我们如何互动、分享和存储数据,还开创了更多自主性与透明度的新时代。
参考文献:
- (
Statista R - Recognizing the Best
)
相关文章:

Web 3.0 介绍
Web 3.0 是互联网的下一代发展阶段,通常被称为去中心化的网络。它与目前的 Web 2.0(以社交媒体、云计算和中心化平台为主导)不同,强调用户对数据和内容的更多掌控,依靠区块链、加密货币、去中心化应用(DApp…...

一起搭WPF界面之界面切换绑定
一起搭WPF界面之界面切换绑定 前言界面填充总结 前言 在主界面中定义Grid网格,界面网格化后,可以模块化搭建界面进行填充。 界面填充 总结 提示:这里对文章进行总结: 例如:以上就是今天要讲的内容,本文仅…...

css 数字比汉字要靠上
这个问题通常是由于数字字体的下排的问题造成的,也就是数字的底部边缘位置比汉字的顶部边缘位置更靠下。为了解决这个问题,可以尝试以下几种方法: 使用CSS的vertical-align属性来调整对齐方式。例如,可以将数字的对齐方式设置为to…...

sentinel原理源码分析系列(三)-启动和初始化
本文是sentinel原理源码分析系列第三篇,分析sentinel启动和初始化 启动/初始化 sentinel初始化分两块,静态初始和适配器(包括aop) 静态初始 1. Root EntranceNode 如果我们用一栋楼类比资源调用,root EntranceNode好比一栋楼的大门&…...

计算机网络(九) —— Tcp协议详解
目录 一,关于Tcp协议 二,Tcp报头字段解析 2.0 协议字段图示 2.1 两个老问题 2.2 16位窗口大小 2.3 32位序号和确认序号 2.4 6个标记位 三,Tcp保证可靠性策略 3.1 确认应答机制(核心) 3.2 超时重传机制 3.3 …...

跨境支付专业术语
跨境支付 跨境支付是指支付或者清结算过程发生在两个及以上的国家地区之间、实现了资金跨国跨地区转移的支付行为。 境外本地支付 境外本地支付是指支付和清结算过程同时发生在单个国家或地区境内,资金在本国家或地区内部转移的支付行为。 国际汇款 国际汇款指跨…...

多级目录SQL分层查询
需求:有多级目录,而目录的层级是不固定的,如下图所示: 数据结构: sql语句: <select id"getList" resultType"com.hikvision.idatafusion.dhidata.bean.vo.knowledgebase.KnowledgeBaseT…...
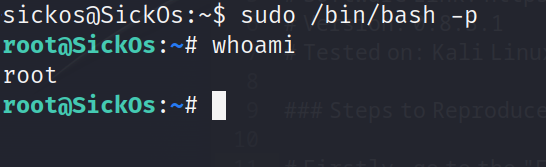
VulnHub-SickOs1.1靶机笔记
SickOs1.1靶机笔记 概述 Vulnhub的靶机sickos1.1 主要练习从互联网上搜取信息的能力,还考察了对代理使用,目录爆破的能力,很不错的靶机 靶机地址: 链接: https://pan.baidu.com/s/1JOTvKbfT-IpcgypcxaCEyQ?pwdytad 提取码: yt…...

【Python】数据可视化之点线图
目录 散点图 气泡图 时序图 关系图 散点图 Scatterplot(散点图)是一种用于展示两个变量之间关系的图表类型。在散点图中,每个观测值(或数据点)都被表示为一个点,其中横轴(…...

jupyter使用pytorch
1、激活环境 以下所有命令都在Anaconda Prompt中操作。 conda activate 环境名称我的环境名称是myenv 如果不知道自己的pytorch配在哪个环境,就用下面方法挨个试。 2、安装jupyter 1、安装 pip install jupyter2、如果已经安装,检查jupyter是否已…...

Electron 安装以及搭建一个工程
安装Node.js 在使用Electron进行开发之前,需要安装 Node.js。 官方建议使用最新的LTS版本。 检查 Node.js 是否正确安装: # 查看node版本 node -v # 查看npm版本 npm -v注意 开发者需要在开发环境安装 Node.js 才能编写 Electron 项目,但是…...

羽毛类型检测系统源码分享
羽毛类型检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of Computer Vis…...
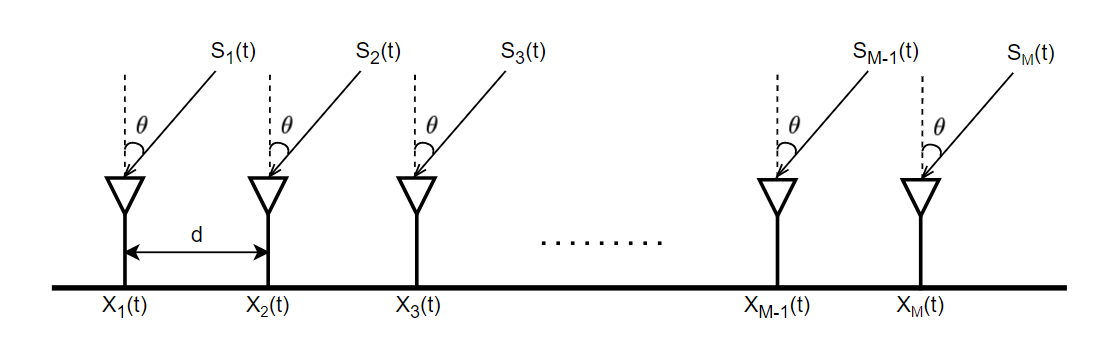
Xiaojie雷达之路---doa估计(dbf、capon、music算法)
Hello,大家好,我是Xiaojie,欢迎大家能够和Xiaojie来一起学习毫米波雷达知识,本篇文章主要是介绍一下雷达信号处理中的dbf、capon、music测角算法,一起来看看吧!!! 前言 本文从信号模型、dbf原理、capon原理、music原理以及代码仿真进行展开描述。 信号模型 阵列接收到…...
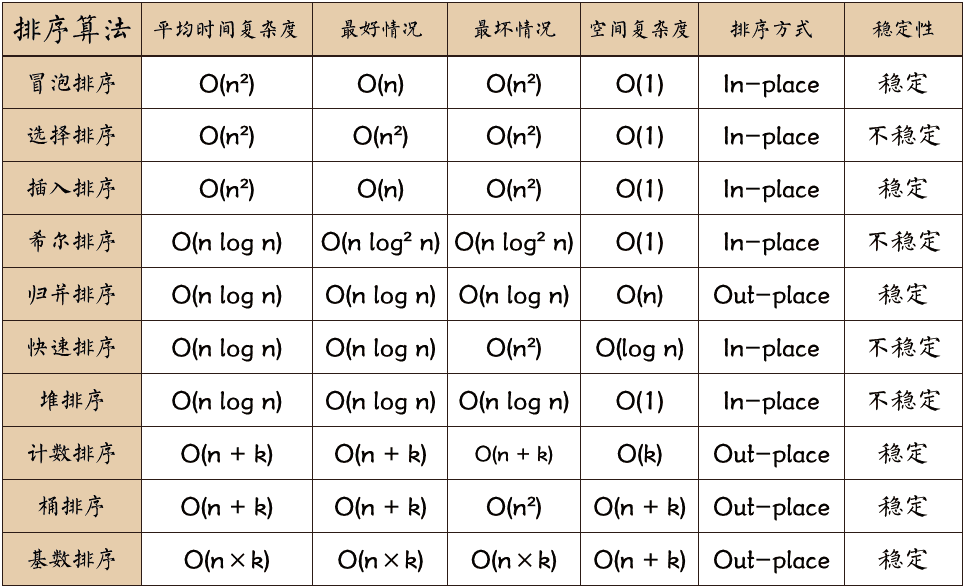
十大排序算法总结
完整文档见 排序算法总结——语雀文档 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破…...
大厂AI必备数据结构与算法——链表(三)详细文档
冲冲冲!开干 神马!神马!神马,一向让我们学习起来抓耳挠腮的数据结构课程竟然也有教程?还那么详细??真的假的? 那么好,胡广告诉你是假的,哈哈哈哈哈哈哈哈哈…...

一键自动化配置OpenHarmony编译环境
一、概述 本工程旨在对Ubuntu一键初始化配置环境,解决OpenHarmony的编译依赖问题,基于本脚本配置后配合一键下载OpenHarmony代码便能轻松掌控OpenHarmony的下载、编译。 当前建议使用稳定分支Itopen-2.0-Release,该分支是经过多次测试OK的&…...
数据集例子)
不同领域的常见 OOD(Out-of-Distribution)数据集例子
以下是几个来自不同领域的常见 OOD(Out-of-Distribution)数据集例子,这些数据集常用于测试和研究模型在分布变化或分布外数据上的泛化能力: 1. 计算机视觉领域 CIFAR-10 vs. CIFAR-10-C / CIFAR-100-C: 描述:CIFAR-10…...

gRPC协议简介
gRPC 是谷歌开源的一套 RPC 协议框架。主要做两件事情:一是数据编码,二是请求映射。 数据编码 数据编码顾名思义就是在将请求的内存对像转化成可以传输的字节流发给服务端,并将收到的字节流再转化成内存对像。方法有很多,常见的…...

[dp+dfs]砝码称重
题目描述 现有 n n n 个砝码,重量分别为 a 1 , a 2 , … , a n a_1, a_2, \ldots,a_n a1,a2,…,an ,在去掉 m m m 个砝码后,问最多能称量出多少不同的重量(不包括 0 0 0 )。 输入格式 第一行为有两个整数…...
)
MYSQL-查看表中字段属性语法(三)
查看表中字段全部信息 show full columns from database_name.table_name; show full columns from table_name;示例 mysql> show full columns from world.city; ----------------------------------------------------------------------------------------------------…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
