胤娲科技:AI界的超级充电宝——忆阻器如何让LLM告别电量焦虑

当AI遇上“记忆橡皮擦”,电量不再是问题!
嘿,朋友们,你们是否曾经因为手机电量不足而焦虑得像个无头苍蝇?想象一下,如果这种“电量焦虑”也蔓延到了AI界,
特别是那些聪明绝顶但“耗电如喝水”的大型语言模型(LLM),比如OpenAI的ο1系列,那场面得多壮观!
每周只能发几十条消息?这哪是AI助手,简直是“限量版聊天机器人”嘛!但别担心,科技界的“脑洞大师”们可不会坐视不管。

最近,Nature杂志就像变魔术一样,甩出了一篇论文,里面提到的“线性对称自选择式14bit动力学分子忆阻器”,简直就是AI界的“超级充电宝”!
这玩意儿听起来高大上,其实你可以把它想象成一块超级智能的“记忆橡皮擦”。不过,它擦的不是你脑中的记忆,而是电路中的“电量焦虑”。
有了它,AI模型就能像吃了菠菜的大力水手一样,力量满满,再也不怕“电量低”的警告弹窗了!
挑战:AI也怕“迷宫”?
你知道吗?AI在处理复杂任务时,经常会遇到一个叫“向量-矩阵乘法”(VMM)的“计算迷宫”。这迷宫里的路弯弯曲曲,一不小心就会迷路。

传统的硬件就像个路痴,走进去就出不来了。但别担心,我们的“记忆橡皮擦”忆阻器,就是那把能打开迷宫之门的金钥匙!
解决方案:忆阻器的“记忆魔法”大显神威
想象一下,你手里有一块神奇的橡皮擦,它能记住你擦掉的每一个字,而且永远不会忘记。这就是忆阻器的魅力所在!
它不仅能限制电流,还能记住之前通过的电荷量,简直就是电路中的“记忆大师”。
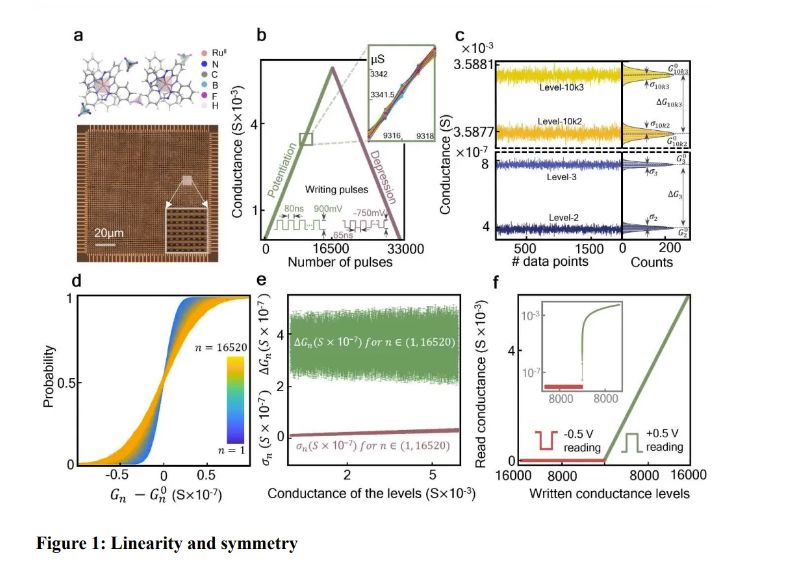
现在,这块“记忆橡皮擦”被做成了一个64×64的交叉开关矩阵,就像是一个超级大的迷宫地图。AI模型只要拿着这张地图,就能轻松找到VMM的出口,再也不用担心迷路了。
而且,这张地图还特别省电,比那些传统的电子计算机要高效得多,简直就是AI界的“节能标兵”!
深入探索:从“创生之柱”到“无限脑洞”
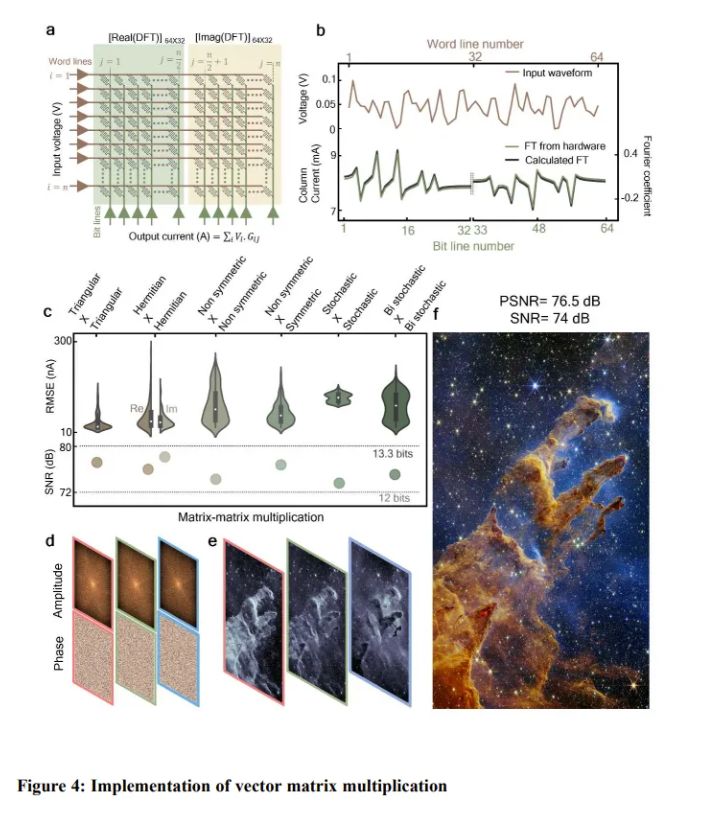
为了证明这块“记忆橡皮擦”的厉害之处,科学家们还做了一个有趣的实验。他们用忆阻器重建了韦伯望远镜观测到的“创生之柱”图像。
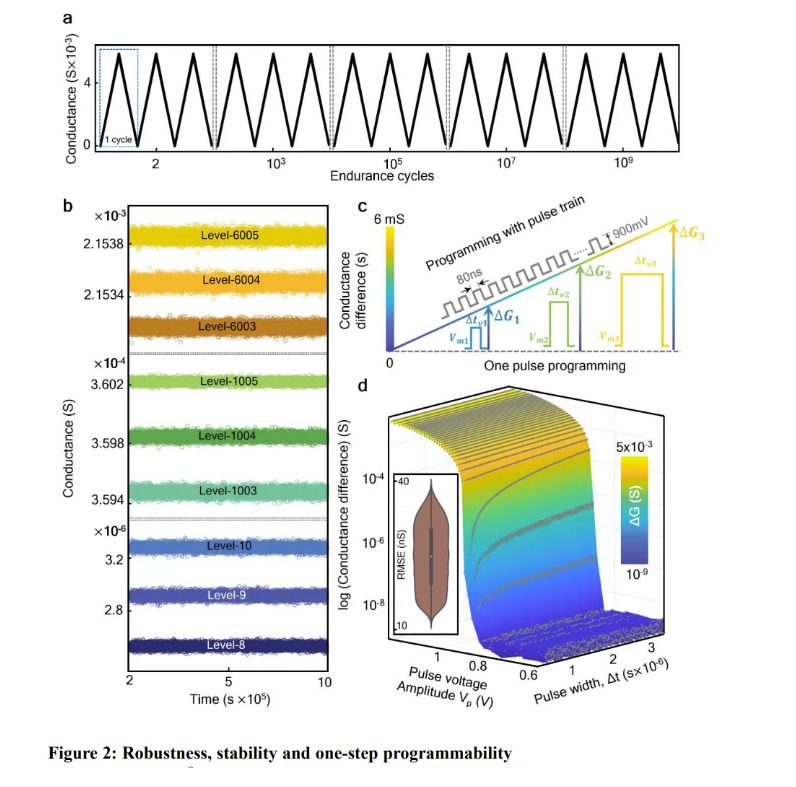
就像是用一块神奇的橡皮擦,把模糊的图片擦得清晰无比。这不仅仅是一个实验的成功,更是对未来AI应用的一次大胆畅想。
AI界的“电力革命”,从“电量焦虑”到“自由飞翔”
朋友们,看到这里,你是不是已经对这块“记忆橡皮擦”充满了期待?它就像AI界的“超级充电宝”,让LLM等大型语言模型彻底告别“电量焦虑”,自由地在知识的海洋中翱翔。
未来已来,让我们拥抱这个充满无限可能的时代。相信在不久的将来,AI将不再受限于电量和成本,而是成为我们生活中最得力的助手和伙伴。
而这一切的起点,正是那块看似不起眼、却拥有无限魔力的“记忆橡皮擦”——忆阻器!

相关文章:

胤娲科技:AI界的超级充电宝——忆阻器如何让LLM告别电量焦虑
当AI遇上“记忆橡皮擦”,电量不再是问题! 嘿,朋友们,你们是否曾经因为手机电量不足而焦虑得像个无头苍蝇?想象一下,如果这种“电量焦虑”也蔓延到了AI界, 特别是那些聪明绝顶但“耗电如喝水”的…...

前端大模型入门:使用Transformers.js手搓纯网页版RAG(二)- qwen1.5-0.5B - 纯前端不调接口
书接上文,本文完了RAG的后半部分,在浏览器运行qwen1.5-0.5B实现了增强搜索全流程。但受限于浏览器和模型性能,仅适合于研究、离线和高隐私场景,但对前端小伙伴来说大模型也不是那么遥不可及了,附带全部代码,…...

K-means聚类分析对比
K-means聚类分析,不同K值聚类对比,该内容是关于K-means聚类分析的,主要探讨了不同K值对聚类结果的影响。K-means聚类是一种常见的数据分析方法,用于将数据集划分为K个不同的类别。在这个过程中,选择合适的K值是非常关键…...

tar命令:压缩、解压的好工具
一、命令简介 用途: tar 命令用于创建归档文件(tarball),以及从归档文件中提取文件。 标签: 文件管理,归档。 特点: 归档文件可以保留原始文件和目录的层次结构,通常使用 .tar …...

Mac电脑上最简单安装Python的方式
背景 最近换了一台新的 MacBook Air 电脑,所有的开发软件都没有了,需要重新配环境,而我现在最常用的开发程序就是Python。这篇文章记录一下我新Mac电脑安装Python的全过程,也给大家一些思路上的提醒。 以下是我新电脑的配置&…...

Linux基础命令cd详解
cd(change directory)命令是 Linux 中用于更改当前工作目录的基础命令。它没有很多复杂的参数,但它的使用非常频繁。以下是 cd 命令的详细说明及示例。 基本语法 cd [选项] [路径] 常用选项 -L : 使用逻辑路径(默认选项&…...

【大模型对话 的界面搭建-Open WebUI】
Open WebUI 前身就是 Ollama WebUI,为 Ollama 提供一个可视化界面,可以完全离线运行,支持 Ollama 和兼容 OpenAI 的 API。 github网址 https://github.com/open-webui/open-webui安装 第一种 docker安装 如果ollama 安装在同一台服务器上&…...

如何在算家云搭建text-generation-webui(文本生成)
一、text-generation-webui 简介 text-generation-webui 是一个流行的用于文本生成的 Gradio Web UI。支持 transformers、GPTQ、AWQ、EXL2、llama.cpp (GGUF)、Llama 模型。 它的特点如下, 3 种界面模式:default (two columns), notebook, chat支持多…...

【Java SE】初遇Java,数据类型,运算符
🔥博客主页🔥:【 坊钰_CSDN博客 】 欢迎各位点赞👍评论✍收藏⭐ 1. Java 概述 1.1 Java 是什么 Java 是一种高级计算机语言,是一种可以编写跨平台应用软件,完全面向对象的程序设计语言。Java 语言简单易学…...

XSS(内含DVWA)
目录 一.XSS的攻击方式: 1. 反射型 XSS(Reflected XSS) 2. 存储型 XSS(Stored XSS) 3. DOM型 XSS(DOM-based XSS) 总结 二..XSS的危害 三.常见的XSS方式 1.script标签 四.常见基本过滤方…...

【SpringCloud】环境和工程搭建
环境和工程搭建 1. 案例介绍1.1 需求1.2 服务拆分服务拆分原则服务拆分⽰例 2. 项目搭建 1. 案例介绍 1.1 需求 实现⼀个电商平台(不真实实现, 仅为演⽰) ⼀个电商平台包含的内容⾮常多, 以京东为例, 仅从⾸⻚上就可以看到巨多的功能 我们该如何实现呢? 如果把这些功能全部…...

基于Java开发的(控制台)模拟的多用户多级目录的文件系统
多级文件系统 1 设计目的 为了加深对文件系统内部功能和实现过程的理解,设计一个模拟的多用户多级目录的文件系统,并实现具体的文件物理结构、目录结构以及较为完善的文件操作命令集。 2 设计内容 2.1系统操作 操作命令风格:本文件系统的…...

tailwindcss group-hover 不生效
无效 <li class"group"><div class"tw-opacity-0 group-hover:tw-opacity-100" /> </li>配了tw前缀,group要改成tw-group // tailwind.config.jsmodule.exports {prefix: "tw-", }<li class"tw-group&q…...
)
python环境配置问题(个人经验)
很久没配置 python 新环境了,最近新项目需要进行配置,在配置过程中发现了不少问题,记录下。 问题1:fatal error: longintrepr.h: 没有那个文件或目录 这个问题的原因是新环境的 python 版本(3.10以上)与本地的版本(3.8.x)差异过…...

BERT训练之数据集处理(代码实现)
目录 1读取文件数据 2.生成下一句预测任务的数据 3.预测下一个句子 4.生成遮蔽语言模型任务的数据 5.从词元中得到遮掩的数据 6.将文本转化为预训练数据集 7.封装函数类 8.调用 import os import random import torch import dltools 1读取文件数据 def _read_wiki(data_d…...
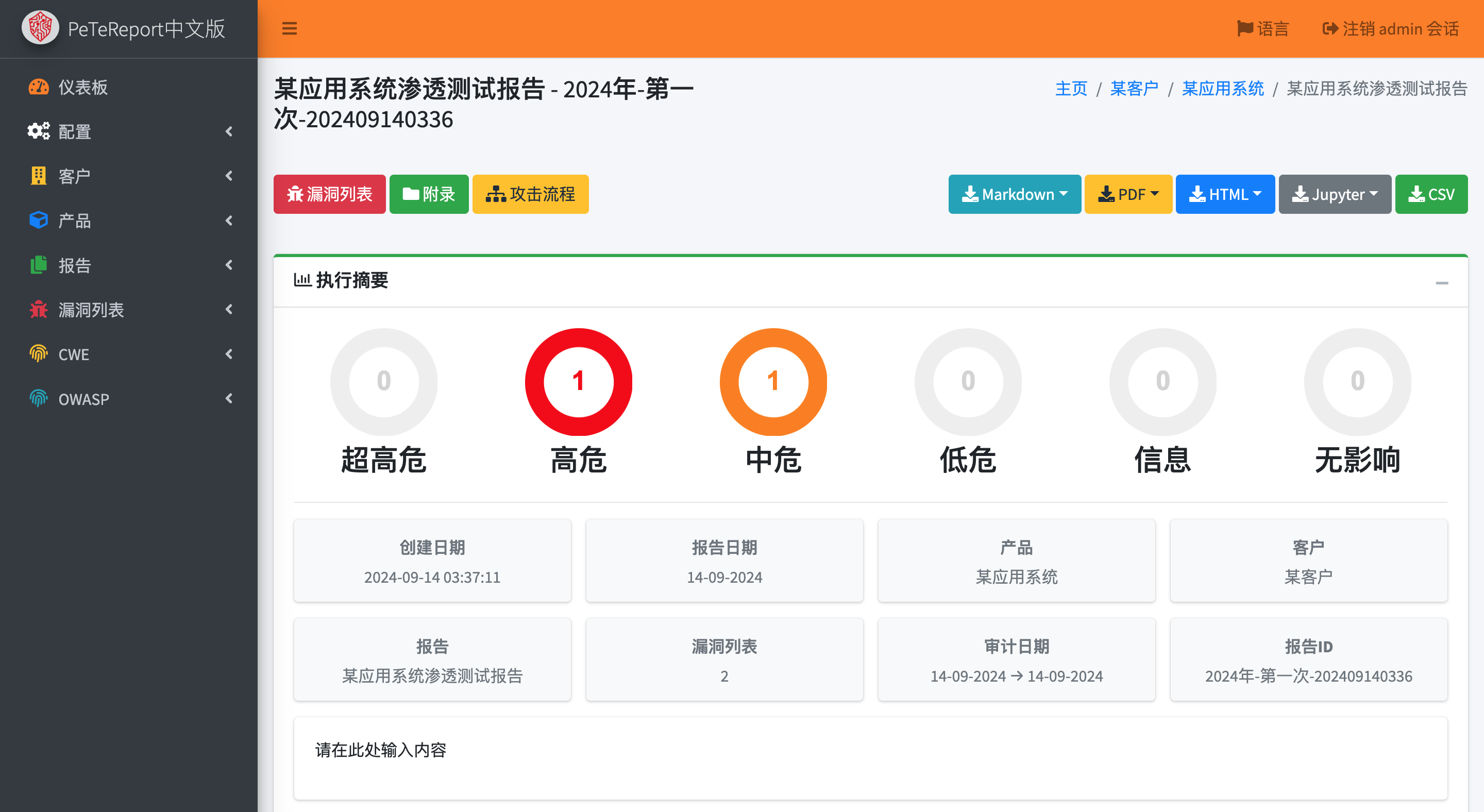
一款辅助渗透测试过程,让渗透测试报告一键生成
《网安面试指南》http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247484339&idx1&sn356300f169de74e7a778b04bfbbbd0ab&chksmc0e47aeff793f3f9a5f7abcfa57695e8944e52bca2de2c7a3eb1aecb3c1e6b9cb6abe509d51f&scene21#wechat_redirect 《Java代码审…...

力扣最热一百题——颜色分类
目录 题目链接:75. 颜色分类 - 力扣(LeetCode) 题目描述 示例 提示: 解法一:不要脸用sort Java写法: 运行时间 解法二:O1指针 Java写法: 重点 运行时间 C写法:…...
2024年工业制造企业CRM研究报告:需求清单、市场格局、案例分析
我国是世界上产业体系最完备的国家,拥有全球规模最大、门类最齐全的生产制造体系,在500种主要工业产品中,有四成以上产品产量位居全球第一。2023年制造业增加值达33万亿元,占世界的比重稳定在30%左右,我国制造业增加值…...

Spring MVC参数接收 总结
1. 简介 Spring MVC可以简化从前端接收参数的步骤。 2. Param传参 通过设定函数入参和添加标记来简化接受: //参数接收 RequestMapping("product") ResponseBody //接受/product?productgoods&id123 //1.名称必须相同,2.不传值不会不…...

Docekrfile和docker compose编写指南及注意事项
Dockerfile 基础语法 我们通过编写dockerfile,将每一层要做的事情使用语法固定下来,之后运行指令就可以通过docker来制作自己的镜像了。 构建镜像的指令:docker build /path -t imageName:tag 注意,docker build后的path必须是dockerfile…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
