UVa The Morning after Halloween 万圣节后的早晨 双向BFS
题目链接:The Morning after Halloween
题目描述:
给定一个二维矩阵,图中有障碍物和字母,你需要把小写字母移动到对应的大写字母位置,不同的小写字母可以同时移动(上下左右四个方向或者保持不动 ),但是移动之后两个字母不能重合,同时移动后不能是两个字母发生了位置的交换。
上图给出了一种情况即该情况下的四种合法移动。
同时题目保证任意一个2×22\times22×2的子区域中一定至少含有一个障碍物,同时边界一定是障碍物。
题解:
我们可以把每个矩阵的看成一个状态进行BFSBFSBFS但是这样状态的个数比较多。
由于题目保证了很小的区域有障碍这也就变相说明了题目可以到达的点并不会很多,所以我们可以把每个可以经过的点进行编号,然后记录字母落在点的编号的三元组(缺少的字母用000来表示,这意味着点的编号需要从111开始),然后将三元组看成是状态,而每一次移动看成是一条边,这样我们只需要进行BFSBFSBFS即可找到目标状态的最少移动次数(在移动的时候,我们需要判断是否违反规则,例如移动后两个字母在同一个位置,或者移动导致两个相邻的字母发生的交换)。由于本题的目标状态也是已知的,那么我们可以使用双向BFSBFSBFS也就是从目标状态和初始状态同时进行BFSBFSBFS当在中间的某个状态相遇的时候,就意味着找到了最少花费,在代码中我们只需要两个队列就可以实现双向BFSBFSBFS一个放入初始状态进行搜索,一个放入目标状态进行搜索。
为什么需要双向BFSBFSBFS?双向BFSBFSBFS通常情况下能够让时间复杂度下降。原理实际上是因为每一次都选择含有较少的节点进行扩展,这样能一定程度上节省时间。
双向BFSBFSBFS的代码应该是每次选择较小的队列进行扩展,而不是轮流进行扩展(如果是轮流进行扩展那么实际上和单向BFSBFSBFS没有太大的差别)。
代码:
#include <bits/stdc++.h>const int DIRECTION_NUM = 5;
const int MAXH = 16 + 1;
const int MAXW = 16 + 1;
const int MAX_NODE = MAXH * MAXW;using namespace std;int w, h, n, nodeNum;
char g[MAXH][MAXW];
int dx[] = {0, 1, -1, 0, 0};
int dy[] = {0, 0, 0, 1, -1};
vector<int> es[MAX_NODE];
int nodeId[MAXH][MAXW];
map<char, int> s, t;
int dis[MAX_NODE][MAX_NODE][MAX_NODE];
int inQ[MAX_NODE][MAX_NODE][MAX_NODE];struct State
{int a, b, c; //最多三个字母位置的结点编号State() {}State(int a, int b, int c) : a(a), b(b), c(c) {}State& operator=(map<char, int> &rhs){a = b = c = 0;auto iter = rhs.begin();for (size_t i = 0; i < n; i++) {if (i == 0) { a = iter->second; }else if (i == 1) { b = iter->second; }else if (i == 2) { c = iter->second; }iter++;}return *this;}
}st, ed;void buildGraph()
{nodeNum = 1;s.clear();t.clear();for (int i = 0; i < MAX_NODE; i++) { es[i].resize(0); }for (int i = 0; i < h; i++) {for (int j = 0; j < w; j++) {if (g[i][j] == '#') { continue; }nodeId[i][j] = nodeNum++;if (islower(g[i][j])) {s[g[i][j]] = nodeId[i][j];} else if (isupper(g[i][j])) {t[g[i][j]] = nodeId[i][j];}}}st = s;ed = t;es[0].push_back(0);for (int i = 0; i < h; i++) {for (int j = 0; j < w; j++) {if (g[i][j] == '#') { continue; }for (int k = 0; k < DIRECTION_NUM; k++) {int nx = i + dx[k];int ny = j + dy[k];if (g[nx][ny] == '#') { continue; }es[nodeId[i][j]].push_back(nodeId[nx][ny]);}}}
}bool conflict(int newA, int newB, int a, int b) { return (newA == newB && newA != 0) || (newA == b && newB == a && newA != 0 && newB != 0); }int bfs(queue<State> &q, int nowQ)
{int size = q.size();int a, b, c;while(size--) {State now = q.front();q.pop();a = now.a, b = now.b, c = now.c;for (auto newA : es[a]) {for (auto newB : es[b]) {if (conflict(newA, newB, a, b)) { continue; }for (auto newC : es[c]) {if (conflict(newA, newC, a, c) || conflict(newB, newC, b, c)) { continue; }if (inQ[newA][newB][newC] == nowQ) { continue; }if (inQ[newA][newB][newC] == 3 - nowQ) { // 在另一个队列中cout << dis[newA][newB][newC] + dis[a][b][c] + 1 << endl;return 0;}dis[newA][newB][newC] = dis[a][b][c] + 1;inQ[newA][newB][newC] = nowQ;q.push({newA, newB, newC});}}}}return -1;
}void dBfs()
{queue<State> qs;queue<State> qt;memset(inQ, 0, sizeof(inQ));qs.push(st);qt.push(ed);dis[st.a][st.b][st.c] = 0;inQ[st.a][st.b][st.c] = 1;dis[ed.a][ed.b][ed.c] = 0;inQ[ed.a][ed.b][ed.c] = 2;while (!qs.empty() && !qt.empty()) {if (qs.size() < qt.size()) { // 优先选择队列短的队列进行bfsif(bfs(qs, 1) != -1) { return; }}else {if(bfs(qt, 2) != -1) { return; };}}
}int main()
{ios::sync_with_stdio(false);while(cin >> w >> h >> n) {if (w == 0 && h == 0 && n == 0) { break; }cin.get(); //读取末尾的换行for (int i = 0; i < h; i++) { cin.getline(g[i], MAXW); } // cin.getline读取的数据末尾没有'\n', cin.getline会保证末尾有结束符0,所以最多读取MAXW-1个有效字符buildGraph();dBfs();}return 0;
}相关文章:

UVa The Morning after Halloween 万圣节后的早晨 双向BFS
题目链接:The Morning after Halloween 题目描述: 给定一个二维矩阵,图中有障碍物和字母,你需要把小写字母移动到对应的大写字母位置,不同的小写字母可以同时移动(上下左右四个方向或者保持不动 ࿰…...
)
Connext DDS属性配置参考大全(3)
Transport传输dds.participant.logging.time_based_logging.process_received_messagedds.participant.logging.time_based_logging.process_received_message.timeout...
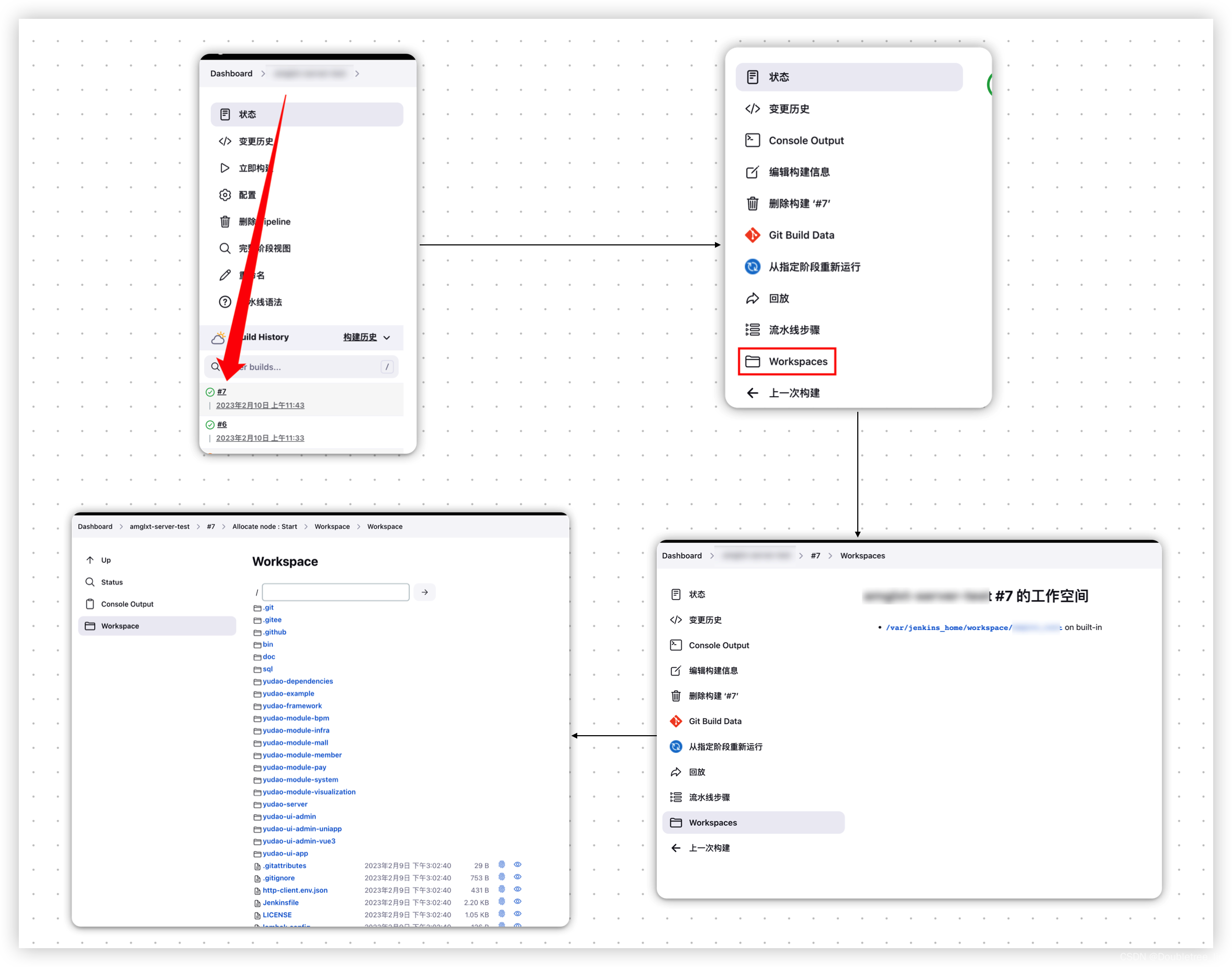
Docker-安装Jenkins-使用jenkins发版Java项目
文章目录0.前言环境背景1.操作流程1.1前期准备工作1.1.1环境变量的配置1.2使用流水线的方式进行发版1.2.1新建流水线任务1.2.2流水线操作工具tools步骤stages步骤1:拉取代码编译步骤2:发送文件并启动0.前言 学海无涯,旅“途”漫漫,“途”中小记ÿ…...

spring 中的 Bean 是否线程安全
文章目录结论1、spring中的Bean从哪里来?2、spring中什么样的Bean存在线程安全问题?3、如何处理spring Bean的线程安全问题?结论 其实,Spring 中的 Bean 是否线程安全,其实跟 Spring 容器本身无关。Spring框架中没有提…...
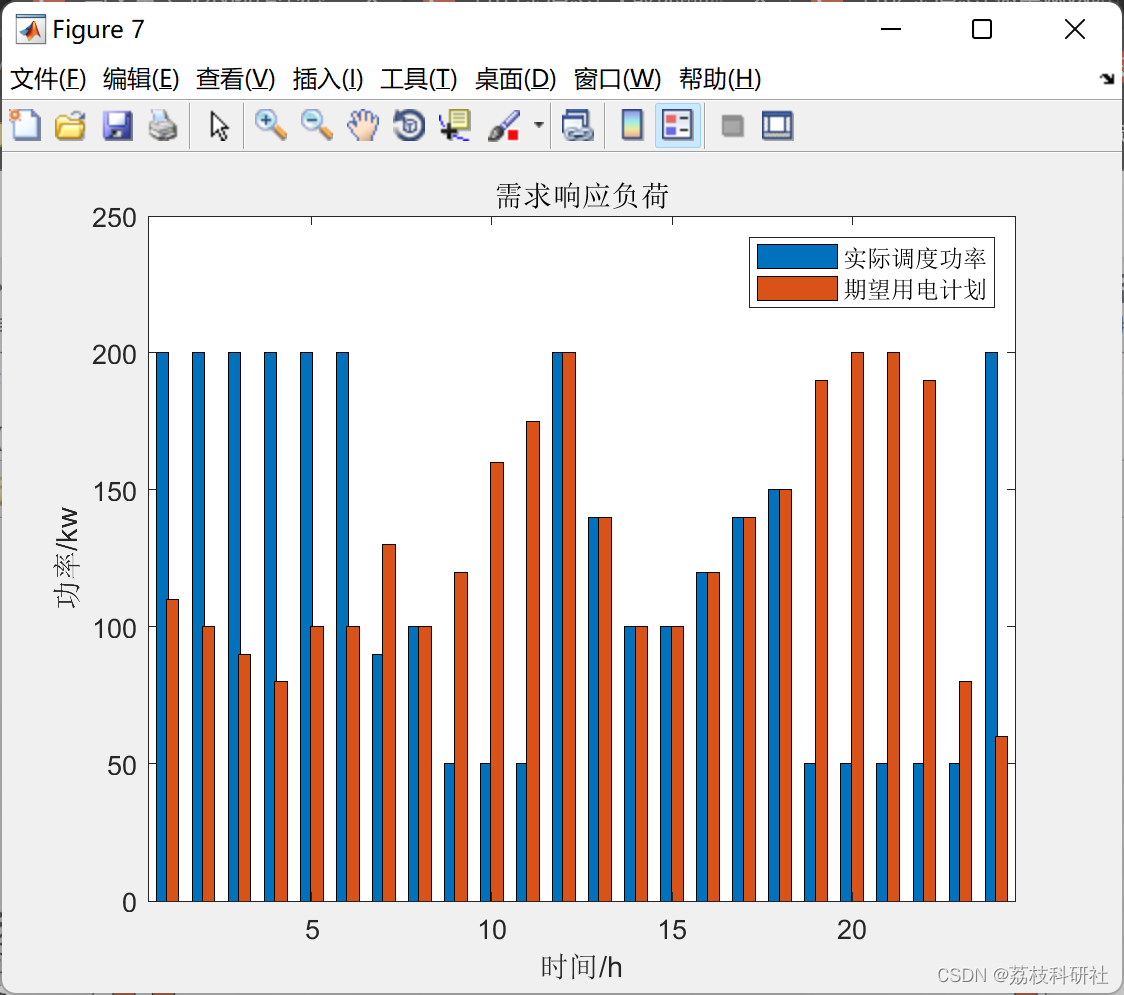
微电网两阶段鲁棒优化经济调度方法[3]【升级优化版本】(Matlab代码实现)
💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑…...

C++入门教程||C++ 数据类型||C++ 变量类型
C 数据类型 使用编程语言进行编程时,需要用到各种变量来存储各种信息。变量保留的是它所存储的值的内存位置。这意味着,当您创建一个变量时,就会在内存中保留一些空间。 您可能需要存储各种数据类型(比如字符型、宽字符型、整型…...
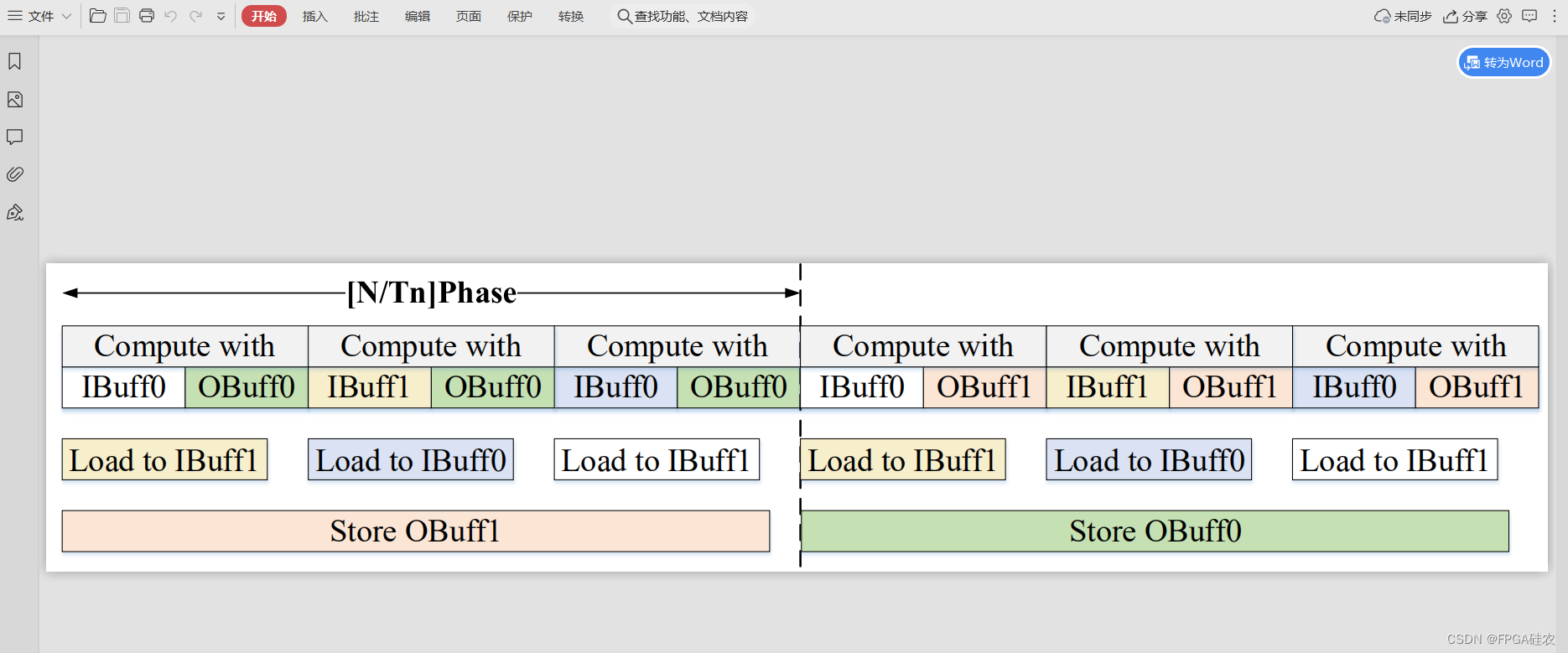
【visio使用技巧】图片导出pdf时去掉多余空白
问题 在visio导出pdf格式的图片时,往往会存在多余的白边,如下图所示: 解决方法 依次点击:菜单栏→文件→选项→自定义功能区→勾选“开发工具”→确定。 依次点击菜单栏→开发工具→显示ShapeSheet→页→Print Properties→将…...

Rust语言之Option枚举类型
概述 Option是Rust语言设计中最重要的枚举类型之一,它编码了其它语言中空值与非空值的概念,差异在于,Rust不会允许你像其它语言一样以非空值的方式来使用一个空值,这避免了很多错误。Option在标准库中的定义如下: pu…...
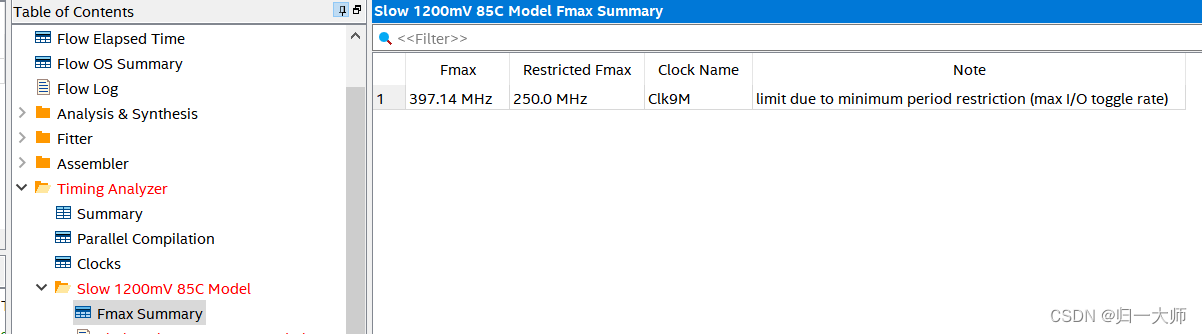
基于TimeQuest时序优化原理和方法
💡 回顾基于RTL逻辑时序优化的基本思路,在关键路径中插入寄存器来优化时序 分析最坏路径 通过前面对TimeQuest软件的理解,基本上可以找到关键路径,此文章主要对关键路径时序进行优化,使设计达到时序要求,以…...

LeetCode第332场周赛
2023.2.12LeetCode第332场周赛 6354. 找出数组的串联值 思路 双指针模拟,两个指针相遇的时候要特判 算法 class Solution { public:long long findTheArrayConcVal(vector<int>& nums) {long long ans 0;int i 0, j nums.size() - 1;while (i <…...

2023-2-12刷题情况
字母板上的路径 题目描述 我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。 在本题里,字母板为board [“abcde”, “fghij”, “klmno”, “pqrst”, “uvwxy”, “z”],如下所示。 我们可以按下面的指令规则行动…...

拉普拉斯矩阵
拉普拉斯算子 Δff(xi1,yj)f(xi−1,yj)f(xi,yj1)f(xi,yj−1)−4f(xi,yj)∑(k,l)∈N(i,j)(f(xk,yl)−f(xi,yj))\begin{aligned} \Delta f & f\left(x_{i1}, y_j\right) f\left(x_{i-1},y_j\right) f\left(x_i,y_{j1}\right)f\left(x_i,y_{j-1}\right) - 4f\left(x_i,y_j\r…...
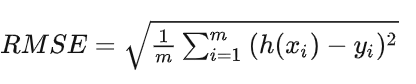
Top-1错误率、Top-5错误率等常见的模型算法评估指标解析
Top-1 错误率:指预测输出的概率最高的类别与人工标注的类别相符的准确率,就是你预测的label取最后概率向量里面最大的那一个作为预测结果,如过你的预测结果中概率最大的那个分类正确,则预测正确,否则预测错误。比如预测…...

Urho3D 容器类型
Urho3D实现了自己的字符串类型和模板容器,而不是使用STL。其基本原理如下: 在某些情况下提高了性能,例如使用PODVector类时。保证字符串和容器的二进制大小,以允许例如嵌入Variant对象内。减少了编译时间。直接命名和实现&#x…...
: 循环结构程序设计)
C语言学习笔记(四): 循环结构程序设计
while语句 定义 While语句是C语言中的循环语句,它按条件循环执行语句,直到条件不满足为止 语法格式如下: while(condition) {//循环体内容; }使用实例 求123…100 include <stdio.h> int main(){int i 1, sum 0;while (i<100){sum i …...

02 OpenCV图像通道处理
1 通道提取与合并 在数字图像处理中,图像通道是指一个图像中的颜色信息被分离为不同的颜色分量。常见的图像通道包括RGB通道、灰度通道、HSV通道等。 RGB通道是指将图像分离为红色、绿色和蓝色三个颜色通道,每个通道表示相应颜色的亮度。这种方式是最常…...
微信小程序图书馆座位预约管理系统
开发工具:IDEA、微信小程序服务器:Tomcat9.0, jdk1.8项目构建:maven数据库:mysql5.7前端技术:vue、uniapp服务端技术:springbootmybatis本系统分微信小程序和管理后台两部分,项目采用…...

有限元分析学习一
系列文章目录 有限元分析学习一 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录系列文章目录前言一、有限元方法的简单介绍1.1 有限元的基础概念1.2 有限元软件发展历史1.3 有限元软件二、弹性力学的简单介绍2.1.…...

android avb2.0 总结
1、android vbmeta结构深入解析 2、android libavb深入解读 看完结构与代码,进一步了解了avb 比如vbmeta的结构、5种描述符、hash公钥签名存储位置 多层vbmeta结构、无vbmeta分区的验证逻辑、hash计算对比、公钥验证、签名验签、5种描述符体的处理 但是还有一些问题没有解决 如…...

聊天机器人-意图识别类,开源库推荐
随着人工智能和自然语言处理技术的不断发展,聊天机器人在商业、教育、医疗等领域的应用越来越广泛。因此,开源聊天机器人代码库也逐渐成为了热门话题。 开源聊天机器人代码库可以帮助开发者快速构建功能强大的聊天机器人,而不必从头开始编写…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
