力扣9.25
2306. 公司命名
给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下:
从 ideas 中选择 2 个 不同 名字,称为 ideaA 和 ideaB 。
交换 ideaA 和 ideaB 的首字母。
如果得到的两个新名字 都 不在ideas 中,那么 ideaA ideaB(串联 ideaA 和 ideaB ,中间用一个空格分隔)是一个有效的公司名字。
否则,不是一个有效的名字。
返回 不同 且有效的公司名字的数目。
数据范围
2 <= ideas.length <= 5 * 1041 <= ideas[i].length <= 10ideas[i]由小写英文字母组成ideas中的所有字符串 互不相同
分析
将字母按开头分类,放入 v e c t o r vector vector中,预处理每个开头对应的集合中的单词在和后面的字母交换首字母后仍然合法的单词的数量,放在 c n t [ i ] [ j ] cnt[i][j] cnt[i][j]中( c n t [ i ] [ j ] cnt[i][j] cnt[i][j]表示以 i i i开头的单词集中若和字符j交换首字母后仍然合法的单词数目),外层循环遍历所有的单词,内存循环遍历字母序比当前单词首字母小的字母,若能交换,则 r e s res res加上 c n t cnt cnt对应的值。
代码
typedef long long LL;
class Solution {
public:const static int N = 35, M = 5e4 + 5;// unordered_map<string, bool> vis;unordered_set<string> st;int cnt[N][N];vector<string> idea[N];long long distinctNames(vector<string>& ideas) {for(auto v : ideas) {// vis[v] = true;st.insert(v);idea[v[0] - 'a'].push_back(v);}for(int i = 'a' - 'a'; i <= 'z' - 'a'; i ++ ) {for(int j = 'a'; j <= 'z'; j ++ ) {for(auto k : idea[i]) {string ts = k;ts[0] = j;// if(!vis[ts]) cnt[i][j - 'a'] ++ ;if(!st.count(ts)) cnt[i][j - 'a'] ++ ;}}}LL res = 0;for(int i = 'a' - 'a'; i <= 'z' - 'a'; i ++ ) {for(auto s : idea[i]) {for(int j = 0; j < i; j ++ ) {string ts = s;ts[0] = char(j + 'a');if(st.count(ts)) continue;res += cnt[j][i];}}}return res * 2;}
};
740. 删除并获得点数
给你一个整数数组 nums ,你可以对它进行一些操作。
每次操作中,选择任意一个 nums[i] ,删除它并获得 nums[i] 的点数。之后,你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。
开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。
数据范围
1 <= nums.length <= 2 * 1041 <= nums[i] <= 104
分析
将每个数字出现的个数用cnt数组记录,令dp[i][0]表示不删除值为i的数获得点数最大值,dp[i][1]表示删除值为i的数获得点数最大值,状态转移如下
- d p [ i ] [ 0 ] = m a x ( d p [ i − 1 ] [ 1 ] , d p [ i − 1 ] [ 0 ] ) dp[i][0]=max(dp[i-1][1],dp[i-1][0]) dp[i][0]=max(dp[i−1][1],dp[i−1][0])
- d p [ i ] [ 1 ] = d p [ i − 1 ] [ 0 ] + c n t [ i ] ∗ i dp[i][1]=dp[i-1][0]+cnt[i]*i dp[i][1]=dp[i−1][0]+cnt[i]∗i
代码
class Solution {
public:const static int N = 1e4 + 5;int cnt[N];int dp[N][2];int n;int deleteAndEarn(vector<int>& nums) {n = nums.size();for(int i = 0; i < n; i ++ ) cnt[nums[i]] ++ ;for(int i = 1; i <= N - 5; i ++ ) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]);dp[i][1] = dp[i - 1][0] + cnt[i] * i;}int res = 0;for(int i = 0; i <= N - 5; i ++ ) {res = max(res, dp[i][0]);res = max(res, dp[i][1]);}return res;}
};
120. 三角形最小路径和
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
数据范围
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
分析
简单DP,注意在边界的情况
代码
class Solution {
public:const static int N = 205;int dp[N][N];int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size();for(int i = 0; i < n; i ++ ) {for(int j = 0; j <= i; j ++ ) {if(j == 0) dp[i + 1][j + 1] = dp[i][j + 1] + triangle[i][j]; else if(j == i) dp[i + 1][j + 1] = dp[i][j] + triangle[i][j]; else dp[i + 1][j + 1] = min(dp[i][j + 1], dp[i][j]) + triangle[i][j];}}int res = 0x3f3f3f3f;for(int i = 0; i < n; i ++ ) res = min(res, dp[n][i + 1]);return res;}
};
相关文章:

力扣9.25
2306. 公司命名 给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下: 从 ideas 中选择 2 个 不同 名字,称为 ideaA 和 ideaB 。 交换 ideaA 和 ideaB 的首字母。 如果得到的两个新名字 都 不在ideas 中,那么 …...

从零开始之AI面试小程序
从零开始之AI面试小程序 文章目录 从零开始之AI面试小程序前言一、工具列表二、开发部署流程1. VMWare安装2. Centos安装3. Centos环境配置3.1. 更改子网IP3.2. 配置静态IP地址 4. Docker和Docker Compose安装5. Docker镜像加速源配置6. 部署中间件6.1. MySQL部署6.2. Redis部署…...
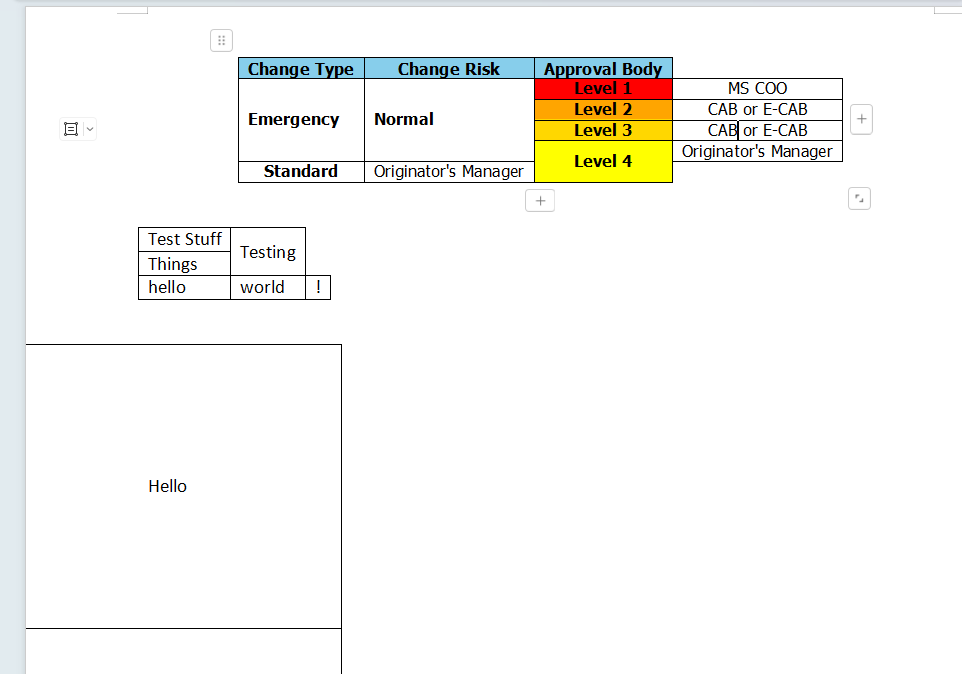
Html2OpenXml:HTML转化为OpenXml的.Net库,轻松实现Html转为Word。
推荐一个开源库,轻松实现HTML转化为OpenXml。 01 项目简介 Html2OpenXml 是一个开源.Net库,旨在将简单或复杂的HTML内容转换为OpenXml组件。 该项目始于2009年,最初是为了将用户评论转换为Word文档而设计的 随着时间的推移,Ht…...

HumanNeRF:Free-viewpoint Rendering of Moving People from Monocular Video 精读
1. 姿态估计和骨架变换模块 人体姿态估计:HumanNeRF 通过已知的单目视频对视频中人物的姿态进行估计。常见的方法是通过人体姿态估计器(如 OpenPose 或 SMPL 模型)提取人物的骨架信息,获取 3D 关节的位置信息。这些关节信息可以帮…...
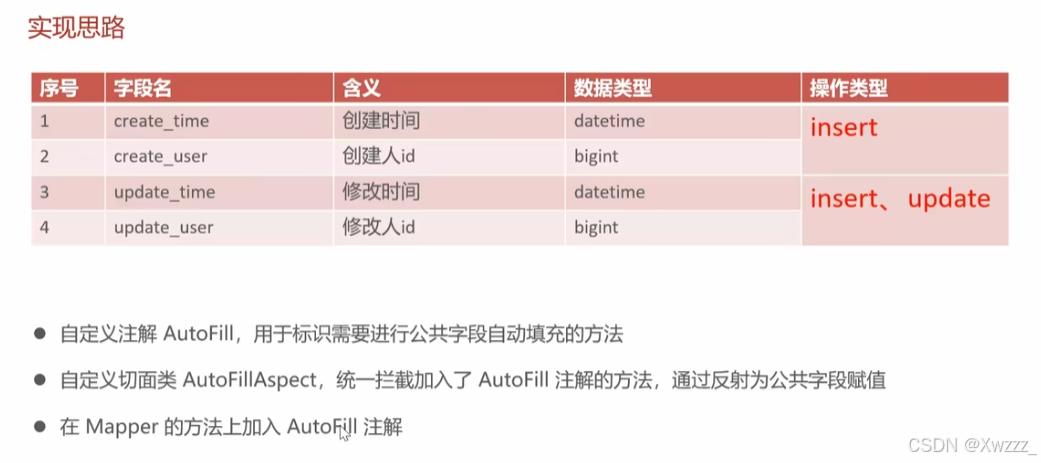
Springboot中基于注解实现公共字段自动填充
1.使用场景 当我们有大量的表需要管理公共字段,并且希望提高开发效率和确保数据一致性时,使用这种自动填充方式是很有必要的。它可以达到一下作用 统一管理数据库表中的公共字段:如创建时间、修改时间、创建人ID、修改人ID等,这些…...

Android 已经过时的方法用什么新方法替代?
过时修正举例 (Kotlin): getColor(): resources.getColor(R.color.white) //已过时// 修正后:ContextCompat.getColor(this, R.color.white) getDrawable(): resources.getDrawable(R.mipmap.test) //已过时//修正后:ContextCompat.getDrawable(this, R.mipmap.test) //…...

【RocketMQ】MQ与RocketMQ介绍
🎯 导读:本文介绍了消息队列(MQ)的基本概念及其在分布式系统中的作用,包括实现异步通信、削峰限流和应用解耦等方面的优势,并对ActiveMQ、RabbitMQ、RocketMQ及Kafka四种MQ产品进行了对比分析,涵…...
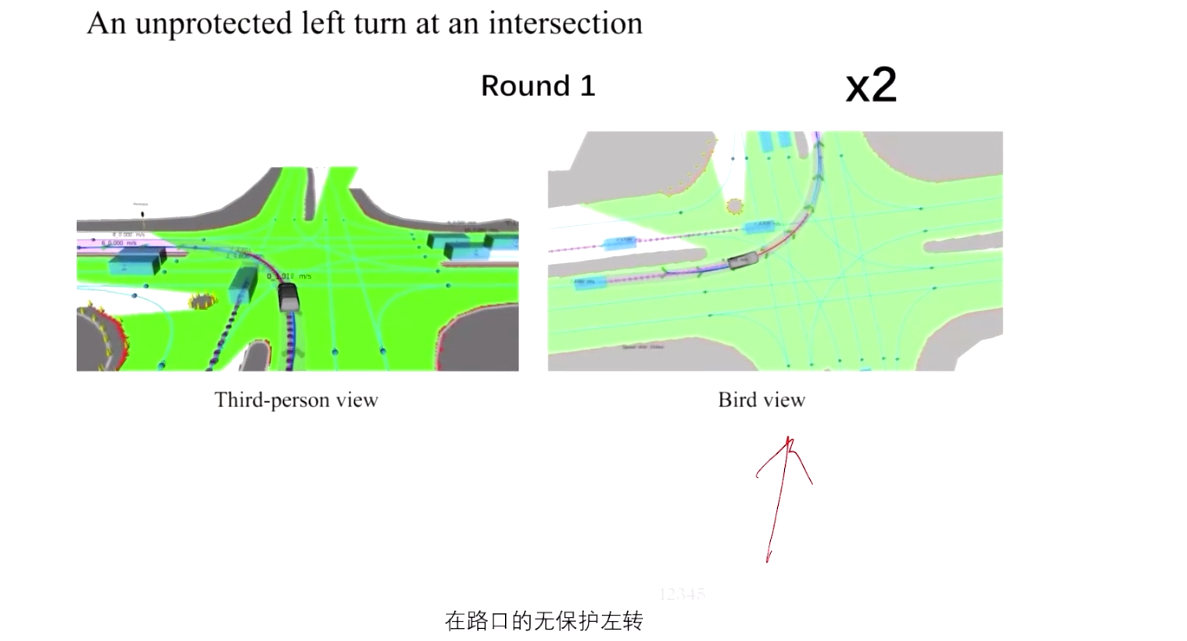
【笔记】自动驾驶预测与决策规划_Part4_时空联合规划
文章目录 0. 前言1. 时空联合规划的基本概念1.1 时空分离方法1.2 时空联合方法 2.基于搜索的时空联合规划 (Hybrid A* )2.1 基于Hybrid A* 的时空联合规划建模2.2 构建三维时空联合地图2.3 基于Hybrid A*的时空节点扩展2.4 Hybrid A* :时空节…...

Linux指令收集
文件和目录操作 ls: 列出目录内容。 -l 显示详细信息。-a 显示隐藏文件(以.开头的文件)。cd: 改变当前工作目录。 cd ~ 返回主目录。cd .. 上移一级目录。pwd: 显示当前工作目录。mkdir: 创建目录。 mkdir -p path/to/directory 创建多级目录。rmdir: 删…...
)
《C++并发编程实战》笔记(五)
五、内存模型和原子操作 5.1 C中的标准原子类型 原子操作是不可分割的操作,它或者完全做好,或者完全没做。 标准原子类型的定义在头文件<atomic>中,类模板std::atomic<T>接受各种类型的模板实参,从而创建该类型对应…...
)
在Python中实现多目标优化问题(5)
在Python中实现多目标优化问题 在Python中实现多目标优化,除了传统的进化算法(如NSGA-II、MOEA/D)和机器学习辅助的方法之外,还有一些新的方法和技术。以下是一些较新的或较少被提及的方法: 1. 基于梯度的多目标优化…...
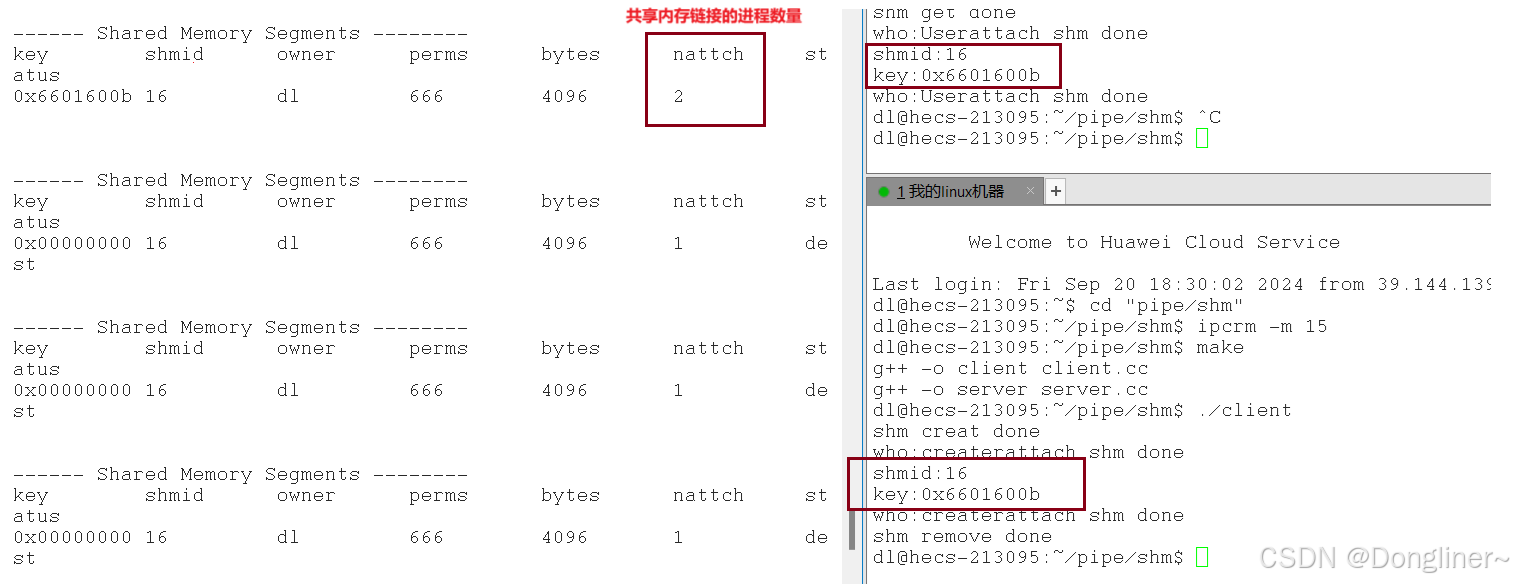
【Linux:共享内存】
共享内存的概念: 操作系统通过页表将共享内存的起始虚拟地址映射到当前进程的地址空间中共享内存是由需要通信的双方进程之一来创建但该资源并不属于创建它的进程,而属于操作系统 共享内存可以在系统中存在多份,供不同个数,不同进…...

今年Java回暖了吗
今年回暖了吗 仅结合师兄和同学的情况 BG 大多双非本 少部分211本 985硕 去年十月一之前 基本转正都失败 十月一之前0 offer 只有很少的人拿到美团 今年十月一之前 有HC的基本都转正了(美团、字节等),目前没有HC的说也有机会(…...

a = Sw,其中a和w是向量,S是矩阵,求w等于什么?w可以写成关于a和S的什么样子的公式
给定公式: a S w a S w aSw 其中: a a a 是已知向量, S S S 是已知矩阵, w w w 是未知向量。 我们的目标是求解 w w w,即将 w w w 表示为 a a a 和 S S S 的函数。 情况 1:矩阵 S S S 可逆 如果矩…...

多线程事务管理:Spring Boot 实现全局事务回滚
多线程事务管理:Spring Boot 实现全局事务回滚 在日常开发中,我们常常会遇到需要在多线程环境下进行数据库操作的场景。这类操作的挑战在于如何保证多个线程中的数据库操作要么一起成功,要么一起失败,即 事务的原子性。尤其是在多个线程并发执行的情况下,确保事务的一致性…...
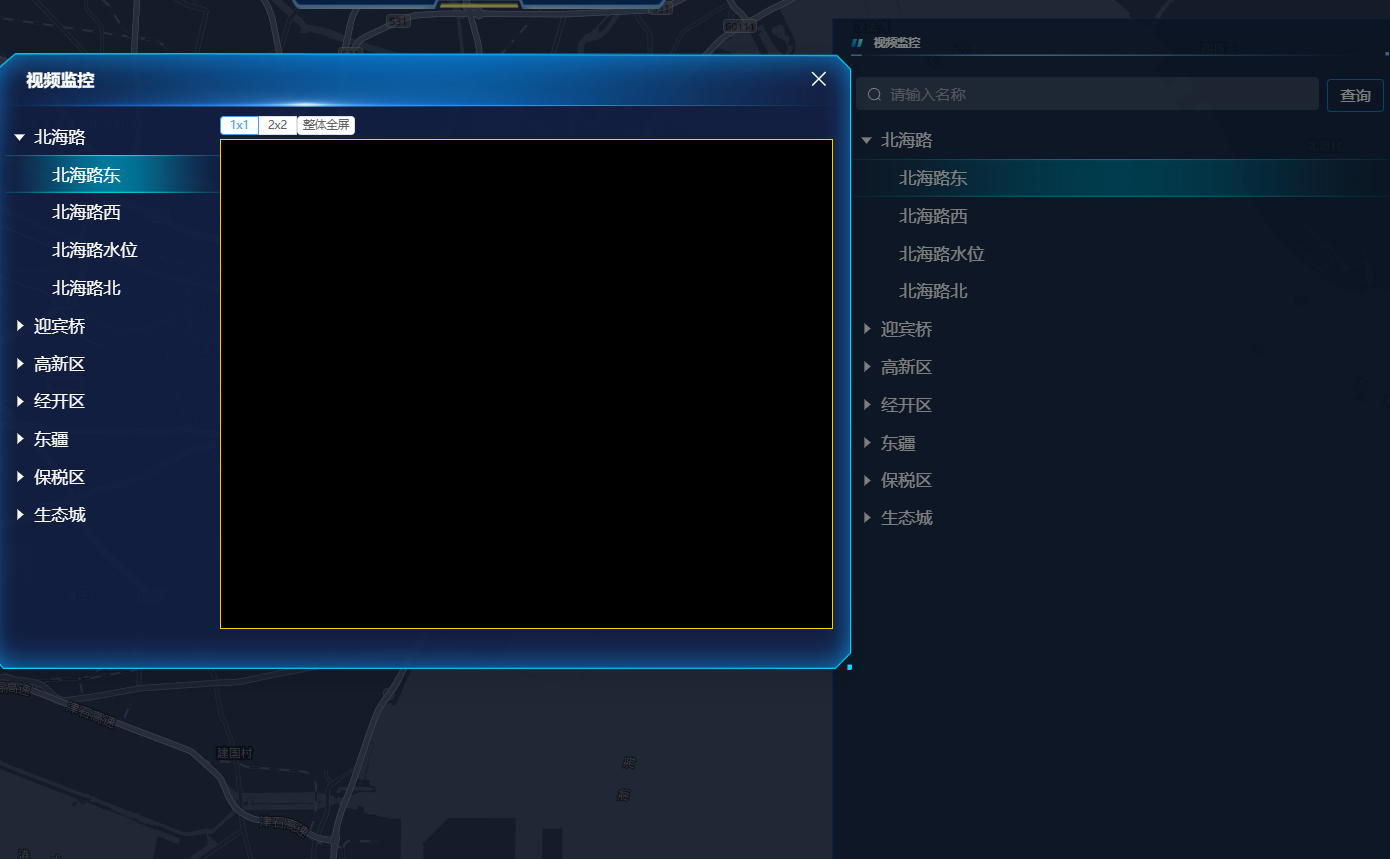
Vue3 中集成海康 H5 监控视频播放功能
🌈个人主页:前端青山 🔥系列专栏:Vue篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来Vuet篇专栏内容:Vue-集成海康 H5 监控视频播放功能 目录 一、引言 二、环境搭建 三、代码解析 子组件部分 1.…...

Linux: eBPF: libbpf-bootstrap-master 编译
文章目录 简介编译运行展示输出展示:简介 这个是使用libbpf的一个例子; 编译 如果是一个可以联网的机器,这个libbpf-bootstrap的编译就方便了,完全是自动化的下载依赖文件;如果没有,就只能自己准备这些个软件。 需要:libbpf-static; [root@RH8-LCP c]# makeLIB …...
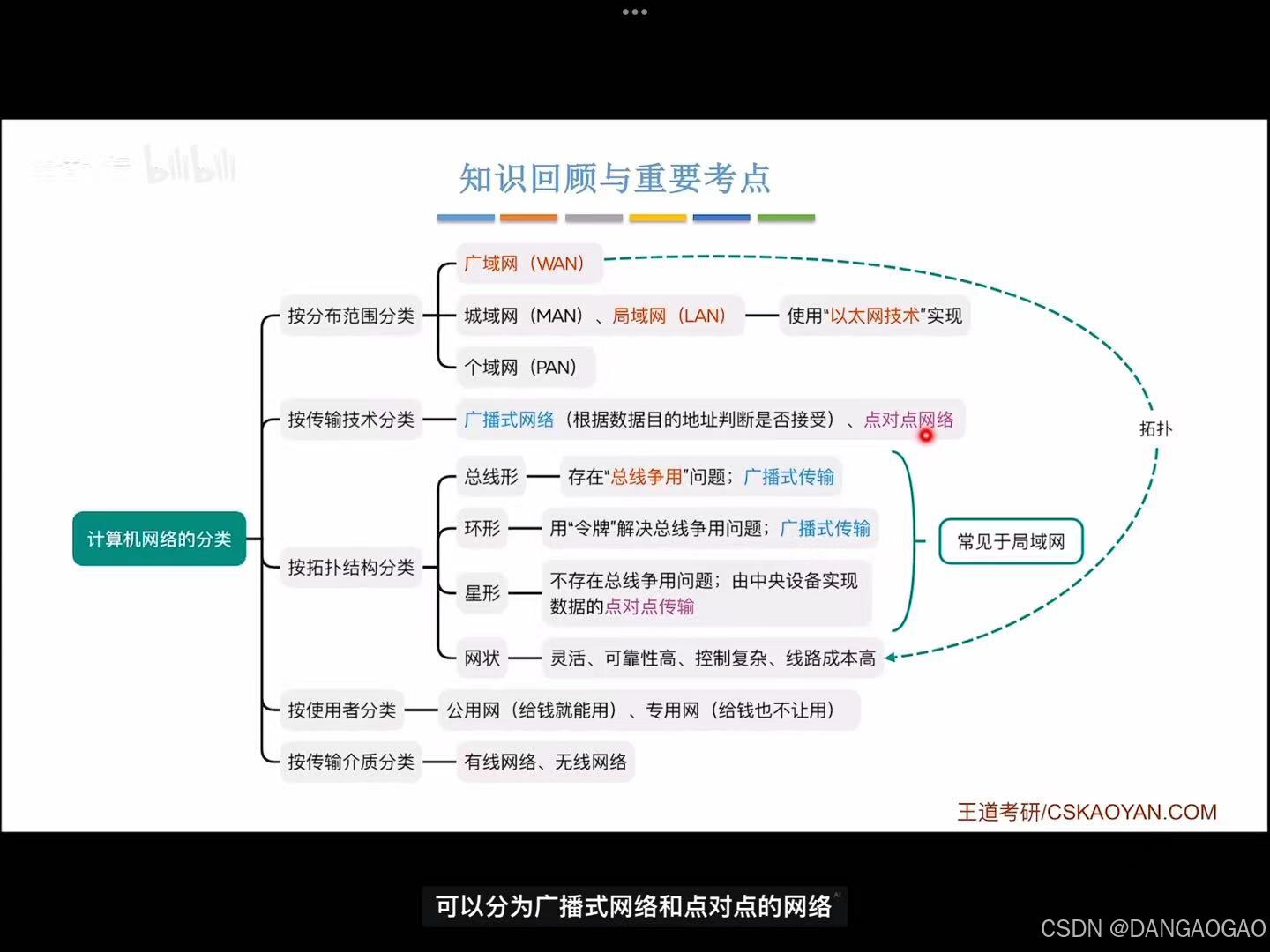
1.1.4 计算机网络的分类
按分布范围分类: 广域网(wan) 城域网(man) 局域网(lan) 个域网(pan) 注意:如今局域网几乎采用“以太网技术实现”,因此“以太网”几乎成了“局域…...

周家庄智慧旅游小程序
项目概述 周家庄智慧旅游小程序将通过数字化手段提升游客的旅游体验,依托周家庄的自然与文化资源,打造智慧旅游新模式。该小程序将结合虚拟现实(VR)、增强现实(AR)和人工智能等技术,提供丰富的…...

【在Linux世界中追寻伟大的One Piece】命名管道
目录 1 -> 命名管道 1.1 -> 创建一个命名管道 1.2 -> 匿名管道与命名管道的区别 1.3 -> 命名管道的打开规则 1.4 -> 例子 1 -> 命名管道 管道应用的一个限制就是只能在具有共同祖先(具有亲缘关系)的进程间通信。如果我们想在不相关的进程之间交换数据&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...
