本省第一所!新大学,揭牌!
9月26日,海南艺术职业学院举行揭牌仪式,标志着海南省第一所公办艺术类高等职业院校正式揭牌成立。海南省旅文厅党组成员、副厅长刘成出席揭牌仪式,省教育厅党组成员、副厅长邢孔政在揭牌仪式上宣读省人民政府同意设立海南艺术职业学院的批复。

刘成在致辞中强调,建设海南艺术职业学院是省委省政府立足海南自由贸易港建设大局,推动文化旅游融合发展,提升海南文化软实力的重大决策部署。学院的成立将为海南培养更多高素质的艺术人才,为文化旅游事业注入新的活力。
今年6月,据教育部公布的全国高校名单显示,海南艺术职业学院获批设立,依托海南省旅游和文化广电体育厅丰富的行业资源优势,整合海南省文化艺术学校、海南省琼剧院、海南省文化馆、海南省艺术研究所、海南省非遗保护中心等力量,利用丰富的艺术创作、演出、展示、培训、研究及非遗保护等行业资源,进一步扩大学院的办学规模,不断充实学院师资力量、实践平台、就业渠道等办学条件。同时,积极吸纳海南省文化艺术骨干企业、龙头企业以及新兴文化产业领域的代表企业或行业协会参与建设,助力学院高质量发展。
该校今年首批设置戏曲表演专业(琼剧方向)、音乐表演专业(器乐方向)2个五年一贯制专业,面向全省招收70名初中毕业生。2025年拟新增招录舞蹈表演(中国舞表演方向)、音乐表演(声乐方向)、室内艺术设计、人物形象设计四个专业。
海南艺术职业学院的揭牌,标志着海南艺术职业教育迈向新高度。未来,海南艺术职业学院将紧紧围绕海南自由贸易港建设需求,培养具有国际视野、创新精神和实践能力的艺术人才。
相关文章:

本省第一所!新大学,揭牌!
9月26日,海南艺术职业学院举行揭牌仪式,标志着海南省第一所公办艺术类高等职业院校正式揭牌成立。海南省旅文厅党组成员、副厅长刘成出席揭牌仪式,省教育厅党组成员、副厅长邢孔政在揭牌仪式上宣读省人民政府同意设立海南艺术职业学院的批复。…...

企业微信(企微)审批与影刀RPA结合
企业微信审批与影刀RPA结合 效果先看视频: 影刀与企业微信审批结合 具体步骤: 1、登录企微管理后台,新建一个审批流。 添加模板→自定义模板,根据需求添加审批节点。 添加完之后,回到审批界面,可以看…...

新手教学系列——用 VSCode 实现高效远程开发
随着软件开发环境日益复杂,远程开发已成为许多开发者的日常工作方式。尤其当项目需要直接在服务器上运行或本地计算资源有限时,能够使用一款便捷、强大的工具至关重要。在众多 IDE 中,VSCode 因其轻量、灵活且支持丰富插件,成为远程开发的理想选择。本文将详细介绍如何通过…...

[uni-app]小兔鲜-04推荐+分类+详情
热门推荐 新建热门推荐组件, 动态设置组件的标题 <template><!-- 推荐专区 --><view class"panel hot"><view class"item" v-for"item in list" :key"item.id">... ...<navigator hover-class"none&…...
PHP人才机遇桥梁招聘求职全能系统小程序源码
人才机遇桥梁 —— 招聘求职全能系统全解析 💼🚀 🌉 搭建人才与机遇的桥梁 在这个竞争激烈的职场环境中,找到一份心仪的工作或招募到合适的人才,往往不是一件容易的事。但幸运的是,我们有了“人才机遇桥梁…...

计算机毕业设计Hadoop+Spark抖音可视化 抖音舆情监测 预测算法 抖音爬虫 抖音大数据 情感分析 NLP 自然语言处理 Hive 机器学习 深度学习
Python抖音可视化开题报告 一、研究背景与意义 随着移动互联网的迅猛发展,短视频平台如抖音已成为人们日常生活中不可或缺的一部分。抖音以其独特的算法和内容推荐机制,吸引了数以亿计的用户。然而,随着用户规模的不断扩大,如何…...

Linux 学习 awk 和sed 命令使用
awk 命令 awk 是一种处理文本文件的语言,是一个强大的文本分析工具。 awk 通过提供编程语言的功能,如变量、数学运算、字符串处理等,使得对文本文件的分析和操作变得非常灵活和高效。 之所以叫 awk 是因为其取了三位创始人 Alfred Aho&#x…...

双端搭建个人博客
1. 准备工作 确保你的两个虚拟机都安装了以下软件: 虚拟机1(Web服务器): Apache2, PHP虚拟机2(数据库服务器): MariaDB2. 安装步骤 虚拟机1(Web服务器) 安装Apache2和PHP 更新系统包列表: sudo apt update安装Apache2: sudo apt install apache2 -y安装PHP及其Apac…...

PHP 面向对象编程
PHP 面向对象编程 PHP 是一种流行的服务器端脚本语言,广泛用于 web 开发。它支持多种编程范式,包括面向对象编程(OOP)。面向对象编程是一种编程风格,它使用“对象”来设计软件,其中对象是数据和行为的集合…...

应急响应(1)-同事电脑
一、现象 重要时间节点,同事反馈桌面有鼠标移动、随机断网;发现登录账户多了一个,由于电脑长时间没有更改过密码,导致忘记密码无法登录。随机联系进行应急处理。 二、排查 2.1、密码重置/删除 由于同事忘记密码导致无法进行登录…...

class 023 随机快速排序
这篇文章是看了“左程云”老师在b站上的讲解之后写的, 自己感觉已经能理解了, 所以就将整个过程写下来了。 这个是“左程云”老师个人空间的b站的链接, 数据结构与算法讲的很好很好, 希望大家可以多多支持左程云老师, 真心推荐. https://space.bilibili.com/8888480?spm_id_f…...

如何理解矩阵的复数特征值和特征向量?
实数特征值的直观含义非常好理解,它就是在对应的特征向量方向上的纯拉伸/压缩。 而复数特征值,我们可以把它放在复数域中理解。但是这里给出一个不那么简洁、但是更加直观的理解方式:把它放在实空间中。那么复数特征值表现的就是旋转等比放大…...

怎么查看网站是否被谷歌收录,查看网站是否被搜索引擎收录5个方法与步骤
要查看网站是否被谷歌(Google)或其他搜索引擎收录,是网站管理和SEO(搜索引擎优化)中的一个重要环节。以下是查看网站是否被搜索引擎收录5个方法与步骤,帮助您确认网站是否被搜索引擎成功索引: …...

Java工具--stream流
Java工具--stream流 过滤(filter)统计求最大最小和均值求和(sum)过滤后,对数据进行统计 遍历(map)规约(reduce)排序(sorted)去重(dist…...
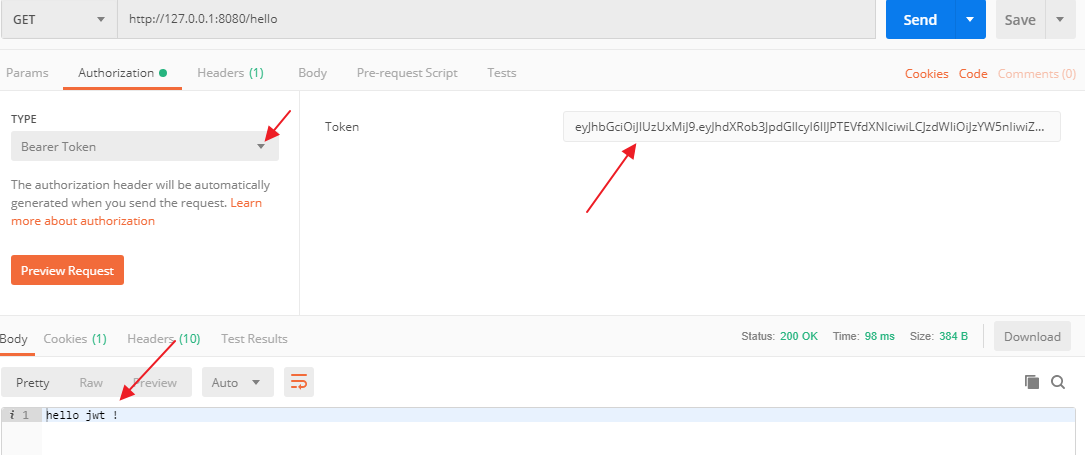
什么是 JWT?它是如何工作的?
松哥最近辅导了几个小伙伴秋招,有小伙伴在面小红书时遇到这个问题,这个问题想回答全面还是有些挑战,松哥结合之前的一篇旧文和大伙一起来聊聊。 一 无状态登录 1.1 什么是有状态 有状态服务,即服务端需要记录每次会话的客户端信…...

微信小程序使用picker,数组怎么设置默认值
默认先显示请选择XXX。然后点击弹出选择列表。如果默认value是0的话,他就直接默认显示数组的第一个了。<picker mode"selector" :value"planIndex" :range"planStatus" range-key"label" change"bindPlanChange&qu…...

Springboot生成树工具类,可通过 id/code 编码生成 2.0版本
优化工具类中,查询父级时便利多次的问题 import org.apache.commons.collections4.CollectionUtils; import org.apache.commons.lang3.mutable.MutableLong; import org.springframework.lang.NonNull; import org.springframework.lang.Nullable; import org.spri…...

17、CPU缓存架构详解高性能内存队列Disruptor实战
1.CPU缓存架构详解 1.1 CPU高速缓存概念 CPU缓存即高速缓冲存储器,是位于CPU与主内存间的一种容量较小但速度很高的存储器。CPU高速缓存可以分为一级缓存,二级缓存,部分高端CPU还具有三级缓存,每一级缓存中所储存的全部数据都是…...

算法训练营打卡Day18
目录 二叉搜索树的最小绝对差二叉搜索树中的众数二叉树的最近公共祖先额外练手题目 题目1、二叉搜索树的最小绝对差 力扣题目链接(opens new window) 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例: 思…...

【leetcode】169.多数元素
boyer-moore算法最简单理解方法: 假设你在投票选人 如果你和候选人(利益)相同,你就会给他投一票(count1),如果不同,你就会踩他一下(count-1)当候选人票数为0&…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
