计算机图形学14:三维图形的投影变换

作者:非妃是公主
专栏:《计算机图形学》
博客地址:https://blog.csdn.net/myf_666
个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩
文章目录
- 专栏推荐
- 专栏系列文章
- 序
- 一、三维图形的投影变换
- 二、平行投影
- 1. 正投影
- Ⅰ. 三视图
- ① 主视图
- ② 俯视图
- ③ 侧视图
- ④ 三视图效果展示
- Ⅱ. 正轴测图
- 2. 斜投影
- Ⅰ. 斜等测图
- Ⅱ. 斜二侧图
- 三、透视投影
- 1. 一点透视
- 四、三维观察基本流程
- the end……
专栏推荐
| 专栏名称 | 专栏地址 |
|---|---|
| 软件工程 | 专栏——软件工程 |
| 计算机图形学 | 专栏——计算机图形学 |
| 操作系统 | 专栏——操作系统 |
| 软件测试 | 专栏——软件测试 |
| 机器学习 | 专栏——机器学习 |
| 数据库 | 专栏——数据库 |
| 算法 | 专栏——算法 |
专栏系列文章
| 文章名称 | 文章地址 |
|---|---|
| 直线生成算法(DDA算法) | 计算机图形学01——DDA算法 |
| 中点BH算法绘制直线 | 计算机图形学02——中点BH算法 |
| 改进的中点BH算法 | 计算机图形学03——改进的中点BH算法 |
| 中点Bresenham画椭圆 | 计算机图形学04——中点BH绘制椭圆 |
| 中点BH算法绘制任意斜率直线 | 计算机图形学05——中点BH算法绘制任意斜率的直线 |
| 中点Bresenham画圆 | 计算机图形学06——中点BH算法画圆 |
| 有效边表法的多边形扫描转换 | 计算机图形学07——有效边表法绘制填充多边形 |
| 中点BH算法绘制抛物线 100x=y2100x = y^2100x=y2 | 计算机图形学08——中点BH绘制抛物线 |
| 二维观察之点的裁剪 | 计算机图形学09——二维观察之点裁剪 |
| 二维观察之线的裁剪 | 计算机图形学10——二维观察之线裁剪 |
| 二维观察之多边形的裁剪 | 计算机图形学11——二维观察之多边形裁剪 |
| 二维图形的几何变换 | 计算机图形学12——二维图形几何变换 |
| 三维图形的几何变换 | 计算机图形学13——三维图形几何变换 |
| 三维图形的投影变换 | 计算机图形学14——三维图形投影变换 |
序
计算机图形学(英语:computer graphics,缩写为CG)是研究计算机在硬件和软件的帮助下创建计算机图形的科学学科,是计算机科学的一个分支领域,主要关注数字合成与操作视觉的图形内容。虽然这个词通常被认为是指三维图形,事实上同时包括了二维图形以及影像处理。
一、三维图形的投影变换
三维图形的投影变换可分为两类:平行投影和透视投影。

二、平行投影
平行投影可分为两类:正投影和斜投影。

1. 正投影
其中正投影中又可以分为:三视图和正轴测图。
Ⅰ. 三视图
① 主视图

主视图是逆着y轴方向去看,所以y轴的坐标为0,进而变化矩阵如下:
Tzox=[1000000000100001]T_{zox}=\begin{bmatrix} 1&0&0&0\\ 0&0&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}\ Tzox=1000000000100001
由于主视图已经落在了xoz平面上,所以不需要其它操作。
代码实现如下:
/// <summary>
/// 将点转化为其次坐标
/// </summary>
/// <param name="vertex">点</param>
/// <returns>齐次坐标</returns>
Matrix vertex3D2qici(VERTEX3D vertex3D) {Matrix qiciVertex(4, 1);qiciVertex.matrix[0][0] = vertex3D.x;qiciVertex.matrix[1][0] = vertex3D.y;qiciVertex.matrix[2][0] = vertex3D.z;qiciVertex.matrix[3][0] = 1;return qiciVertex;
}VERTEX3D qici2vertex3D(Matrix qici) {VERTEX3D res;res.x = qici.matrix[0][0];res.y = qici.matrix[1][0];res.z = qici.matrix[2][0];return res;
}VERTEX3D mainViewTransform3D(VERTEX3D vertex3D) {Matrix qiciVertex = vertex3D2qici(vertex3D);Matrix transform; // 去掉y坐标变换矩阵transform.matrix[0][0] = 1;transform.matrix[1][1] = 0;transform.matrix[2][2] = 1;transform.matrix[3][3] = 1;Matrix qicires = dotMatrix(transform, qiciVertex);VERTEX3D res = qici2vertex3D(qicires); return res;
}
② 俯视图
俯视图逆着z轴的方向来看,因此需要将z轴上的坐标置为0,第一步变换矩阵如下:
Txoy=[1000010000000001]T_{xoy}=\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&0&0\\ 0&0&0&1\\ \end{bmatrix}\ Txoy=1000010000000001
同时由于最终要是的三个视图落在一个平面内(xoz平面),因此还需要对视图进行旋转,使得俯视图绕着x轴旋转-90度,第二度变换矩阵如下:
TRx=[10000cosθ−sinθ00sinθcosθ00001]=[100000100−1000001]T_{Rx}=\begin{bmatrix} 1&0&0&0\\ 0&cos\theta&-sin\theta&0\\ 0&sin\theta&cos\theta&0\\ 0&0&0&1\\ \end{bmatrix}=\begin{bmatrix} 1&0&0&0\\ 0&0&1&0\\ 0&-1&0&0\\ 0&0&0&1\\ \end{bmatrix} TRx=10000cosθsinθ00−sinθcosθ00001=100000−1001000001
此处 θ=−90∘\theta=-90^{\circ}θ=−90∘
最后还要将主视图和俯视图分开,保持一定间距,还要让俯视图向下平移一个单位向量 −z0-z_0−z0。
TTz=[10000100001−z00001]T_{Tz}=\begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&-z_0\\ 0&0&0&1\\ \end{bmatrix} TTz=10000100001000−z01
所以总变换矩阵如下:
p′=TTz⋅TRx⋅Txoy⋅pp'=T_{Tz}\cdot T_{Rx}\cdot T_{xoy}\cdot p p′=TTz⋅TRx⋅Txoy⋅p
VERTEX3D topViewTransform3D(VERTEX3D vertex3D) {Matrix qiciVertex = vertex3D2qici(vertex3D);Matrix transform1; // 去掉z坐标变换矩阵transform1.matrix[0][0] = 1;transform1.matrix[1][1] = 1;transform1.matrix[2][2] = 0;transform1.matrix[3][3] = 1;Matrix qicitmp = dotMatrix(transform1, qiciVertex); // 去掉z坐标VERTEX3D tmp = qici2vertex3D(qicitmp);tmp = rotationForXTransform3D(tmp, -90); // 沿x轴旋转90度tmp = transTransform3D(tmp, 0, 0, -100); // 向下平移-1个单位return tmp;
}
③ 侧视图
侧视图为逆着x轴看,所以要将x方向的坐标置为0:
Tyoz=[0000010000100001]T_{yoz}=\begin{bmatrix} 0&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} Tyoz=0000010000100001
同理,为了与主视图画在一个平面内,使侧视面绕z轴旋转90∘90^{\circ}90∘,如下:
TRx=[cosθ−sinθ00sinθcosθ0000100001]=[0−100100000100001]T_{Rx}=\begin{bmatrix} cos\theta&-sin\theta&0&0\\ sin\theta&cos\theta&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}=\begin{bmatrix} 0&-1&0&0\\ 1&0&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} TRx=cosθsinθ00−sinθcosθ0000100001=0100−100000100001
然后与主视图有一定间距,向x轴负方向平移−x0-x_0−x0,如下:
TTx=[100−x0010000100001]T_{Tx}=\begin{bmatrix} 1&0&0&-x_0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} TTx=100001000010−x0001
所以总变换矩阵如下:
p′=TTx⋅TRz⋅Tyoz⋅pp'=T_{Tx}\cdot T_{Rz}\cdot T_{yoz}\cdot p p′=TTx⋅TRz⋅Tyoz⋅p
实现代码如下:
VERTEX3D sideViewTransform3D(VERTEX3D vertex3D) {Matrix qiciVertex = vertex3D2qici(vertex3D);Matrix transform1; // 去掉x坐标变换矩阵transform1.matrix[0][0] = 0;transform1.matrix[1][1] = 1;transform1.matrix[2][2] = 1;transform1.matrix[3][3] = 1;Matrix qicitmp = dotMatrix(transform1, qiciVertex); // 去掉x坐标VERTEX3D tmp = qici2vertex3D(qicitmp);tmp = rotationForZTransform3D(tmp, 90); // 沿x轴旋转90度tmp = transTransform3D(tmp, -100, 0, 0); // 向x负方向平移-1个单位return tmp;
}
④ 三视图效果展示

测试效果代码:
void testThreeView() {VERTEX3D vertex3D_1 = { 100,100,100 };VERTEX3D vertex3D_2 = { 0,100,0 };VERTEX3D vertex3D_3 = { 200,100,0 };VERTEX3D vertex3D_4 = { 200,0,0 };// 主视图VERTEX3D res1 = mainViewTransform3D(vertex3D_1);VERTEX3D res2 = mainViewTransform3D(vertex3D_2);VERTEX3D res3 = mainViewTransform3D(vertex3D_3);VERTEX3D res4 = mainViewTransform3D(vertex3D_4);glBegin(GL_LINES);glVertex2f(-res1.x, res1.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res1.x, res1.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res1.x, res1.z);glVertex2f(-res4.x, res4.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res4.x, res4.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res4.x, res4.z);glEnd();// 上视图res1 = topViewTransform3D(vertex3D_1);res2 = topViewTransform3D(vertex3D_2);res3 = topViewTransform3D(vertex3D_3);res4 = topViewTransform3D(vertex3D_4);glBegin(GL_LINES);glVertex2f(-res1.x, res1.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res1.x, res1.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res1.x, res1.z);glVertex2f(-res4.x, res4.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res4.x, res4.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res4.x, res4.z);glEnd();// 侧视图res1 = sideViewTransform3D(vertex3D_1);res2 = sideViewTransform3D(vertex3D_2);res3 = sideViewTransform3D(vertex3D_3);res4 = sideViewTransform3D(vertex3D_4);glBegin(GL_LINES);glVertex2f(-res1.x, res1.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res1.x, res1.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res1.x, res1.z);glVertex2f(-res4.x, res4.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res2.x, res2.z);glVertex2f(-res4.x, res4.z);glVertex2f(-res3.x, res3.z);glVertex2f(-res4.x, res4.z);glEnd();cout << res1.x << " " << res1.z << endl;
}// 显示图形
void Display(void) {glClear(GL_COLOR_BUFFER_BIT); //用当前背景色填充窗口// 此处需增加调用基本图形生成函数glColor3f(0.0f, 0.0f, 0.0f); //设置当前的绘图颜色为红色glBegin(GL_LINES);glVertex2d(-400, 0);glVertex2d(400, 0);glVertex2d(0, 300);glVertex2d(0, -300);glEnd();glColor3f(1.0f, 0.0f, 0.0f); //设置当前的绘图颜色为红色testThreeView();glFlush(); //处理所有的OpenGL程序
}// 初始化OpenGL场景
void Initial() {glClearColor(1.0f, 1.0f, 1.0f, 1.0f); //设置窗口背景颜色为白色glMatrixMode(GL_PROJECTION); //设置投影参数gluOrtho2D(-400.0, 400.0, -300, 300.0); // 投影面上的模型坐标范围
}int main(int argc, char* argv[]) {//testTransTransform();//testScaleTransform3D();//testSymmetryForXTransform3D();//testSymmetryForYTransform3D();//testSymmetryForZTransform3D();//testSymmetryForXOYTransform3D();//testSymmetryForYOZTransform3D();//testSymmetryForZOXTransform3D();//testMiscutTransform3D();//testRotationForXTransform3D();//testRotationForYTransform3D();//testRotationForZTransform3D();//testThreeView();glutInit(&argc, argv); // glut初始化glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);//初始窗口显示模式glutInitWindowSize(800, 600); //设置窗口的尺寸glutInitWindowPosition(200, 200); //设置窗口的位置glutCreateWindow("基本图形生成"); //创建一个窗口glutDisplayFunc(Display); //设置当前窗口的显示回调函数Initial(); //完成窗口初始化glutMainLoop(); //启动主GLUT事件处理循环 return 0;
}
其中旋转函数的定义,见专栏中文章(计算机图形学:三维图形的几何变换),其中有关于用到的几何变换函数的详细定义。
Ⅱ. 正轴测图


三视图与正轴测都属于正投影,但各有优缺点,如下:

按照投影面与三个坐标轴之间的夹角,可以分为等轴测、正二侧、正三侧。

正轴测的变换矩阵与公式推导:






2. 斜投影
斜轴测图:将三维物体向一个单一的投影面做平行投影,但投影方向不垂直于投影面所得的平面图形。常用的斜轴侧图有斜等侧图和斜二侧图。

Ⅰ. 斜等测图
后面用到了补充……
Ⅱ. 斜二侧图
后面用到了补充……
三、透视投影









1. 一点透视


两点透视和三点透视较为复杂,在此不再展开介绍。
四、三维观察基本流程

这里还有些不懂,懂了的时候再来补充 hahaha~ ヾ(≧▽≦*)o
the end……
三维图形的几何变换到这里就要结束啦~~到此既是缘分,欢迎您的点赞、评论、收藏!关注我,不迷路,我们下期再见!!
😘😘😘 我是Cherries,一位计算机科班在校大学生,写博客用来记录自己平时的所思所想!
💞💞💞 内容繁杂,又才疏学浅,难免存在错误,欢迎各位大佬的批评指正!
👋👋👋 我们相互交流,共同进步!
注:本文由
非妃是公主发布于https://blog.csdn.net/myf_666,转载请务必标明原文链接:https://blog.csdn.net/myf_666/article/details/129877371
相关文章:

计算机图形学14:三维图形的投影变换
作者:非妃是公主 专栏:《计算机图形学》 博客地址:https://blog.csdn.net/myf_666 个性签:顺境不惰,逆境不馁,以心制境,万事可成。——曾国藩 文章目录专栏推荐专栏系列文章序一、三维图形的投…...
第二课)
【ChatGPT4】王老师零基础《NLP》(自然语言处理)第二课
我的已经在起、点开了书《王老师带我成为救世主》,那个更新及时 (1)---------------------------------------------------------------------------------------- 我: 1我/喜欢/吃/苹果,因为/它/们/很/好吃。 2 Th…...

设计模式之中介者模式在前端的应用
文章目录中介者模式在前端的应用场景1.实现组件之间的松耦合2. 实现异步请求的协同3. 实现事件驱动的编程模型4. 实现复杂交互的协调总结中介者模式在前端的应用场景 中介者模式是一种常见的设计模式,它可以将对象之间的通信集中处理,从而提高系统的可维…...

2023年还能入行程序员吗?工作3年以上的黑马老学员怎么说?
很多人觉得,毕业3年,不过是毕业第1年的重复,键盘Ctrl、C和V键磨损更严重了。妥妥属于光涨年龄,不涨经验;只涨体重,不涨工资…… 他们不理解,为什么同样的起跑线,有人发展神速&#…...

接收机的噪声来源与噪声分析
噪声分类 射频接收机中的噪声主要可以分为两类:内部噪声和外部噪声。 内部噪声 内部噪声主要来自于接收机内部的放大器、混频器、本振等元件所产生的噪声。根据不同的产生机制,内部噪声可以分为以下几类: a. 电感噪声:由于电感…...

Android FrameWork——SystemServer
Android系统在启动的时候有两个非常重要的进程,一个是Zygote,另一个就是system_server。SystemServer是系统用来启动service的入口,比如我们常用的AMS,WMS,PMS等等都是由它创建的。 system_server进程的启动 system_…...

婴儿推车ASTMF883测试
1.cpc认证是总称,cpc认证下边有很多的标准,常见的有ASTM F963(铅含量)、CPSIA(邻苯8P)、ASTM F833(婴儿车)等; 2.婴儿车ASTM认证是什么 2019年8月2日,美国消…...
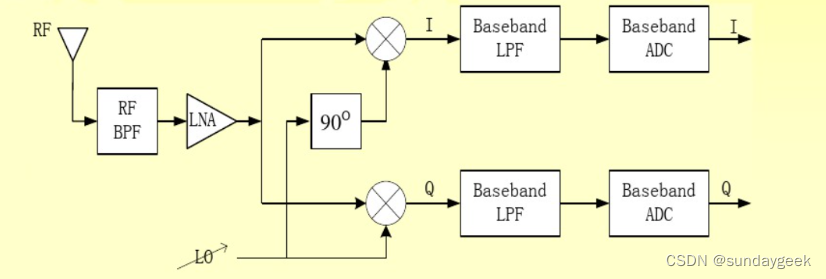
射频接收机概述
接收机架构 射频接收机架构是指电子设备中用于接收无线电信号的部分。它通常由前置放大器、中频放大器、混频器、局部振荡器和带通滤波器等组成。以下是一个基本的射频接收机架构: 前置放大器:前置放大器的作用是放大接收天线接收到的微弱无线电信号&am…...

实验三Numpy知识点总结
熟悉和使用NumPy模块 import numpy as np一、完成下列数组操作与运算。 (1)创建2行4列的数组arr_a,数组中的元素为0至7,要求用arange()函数创建。 arr_anp.arange(8) arr_a.resize(2,4) print(arr_a)[[0 1 2 3][4 5 6 7]]&…...

Code Review时学到的技巧之isAssignableFrom
🍊 Java学习:Java从入门到精通总结 🍊 深入浅出RocketMQ设计思想:深入浅出RocketMQ设计思想 🍊 绝对不一样的职场干货:大厂最佳实践经验指南 📆 最近更新:2023年4月1日 …...

IP协议以及相关技术
这里写目录标题前言正文IP基本认识IP的作用IP和MAC的关系IP地址的基础知识IP地址定义IP地址分类(IPv4)无分类IP地址CIDR子网掩码IPv6基础知识相关技术DNS域名解析ARPDHCPNATICMPIGMP总结参考连接前言 大家好,我是练习两年半的Java练习生,今天我们来讲一…...
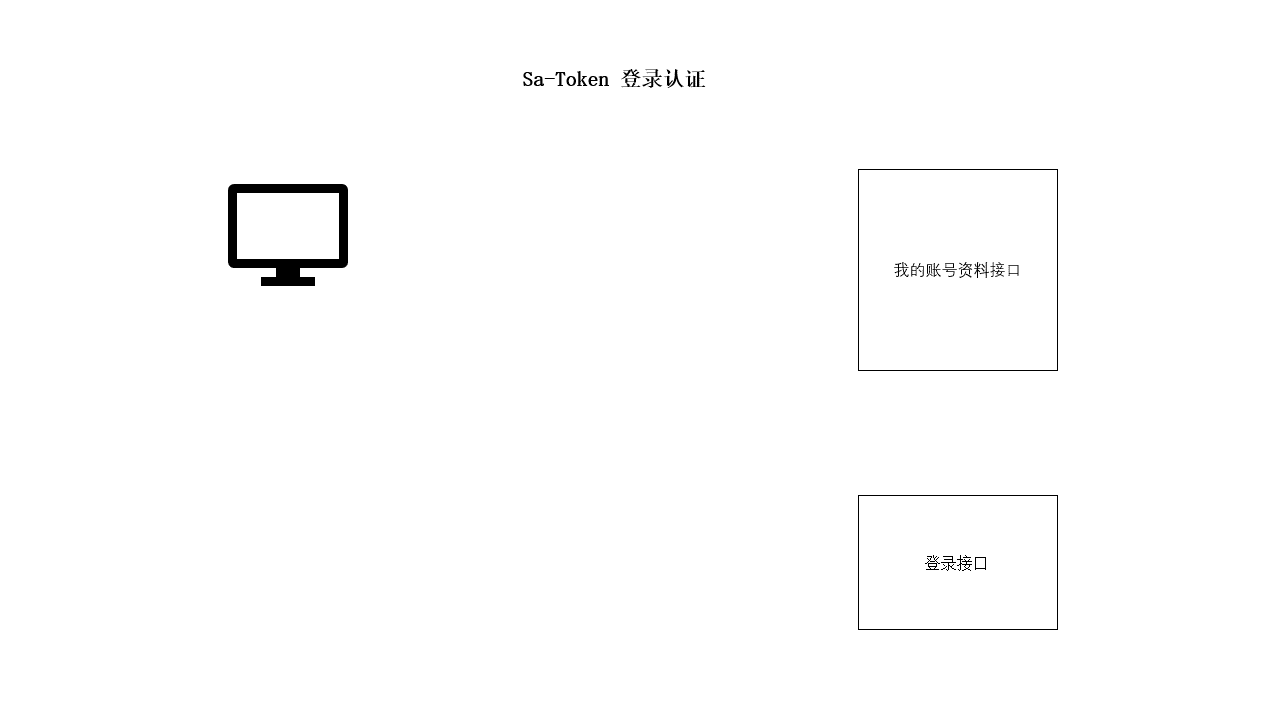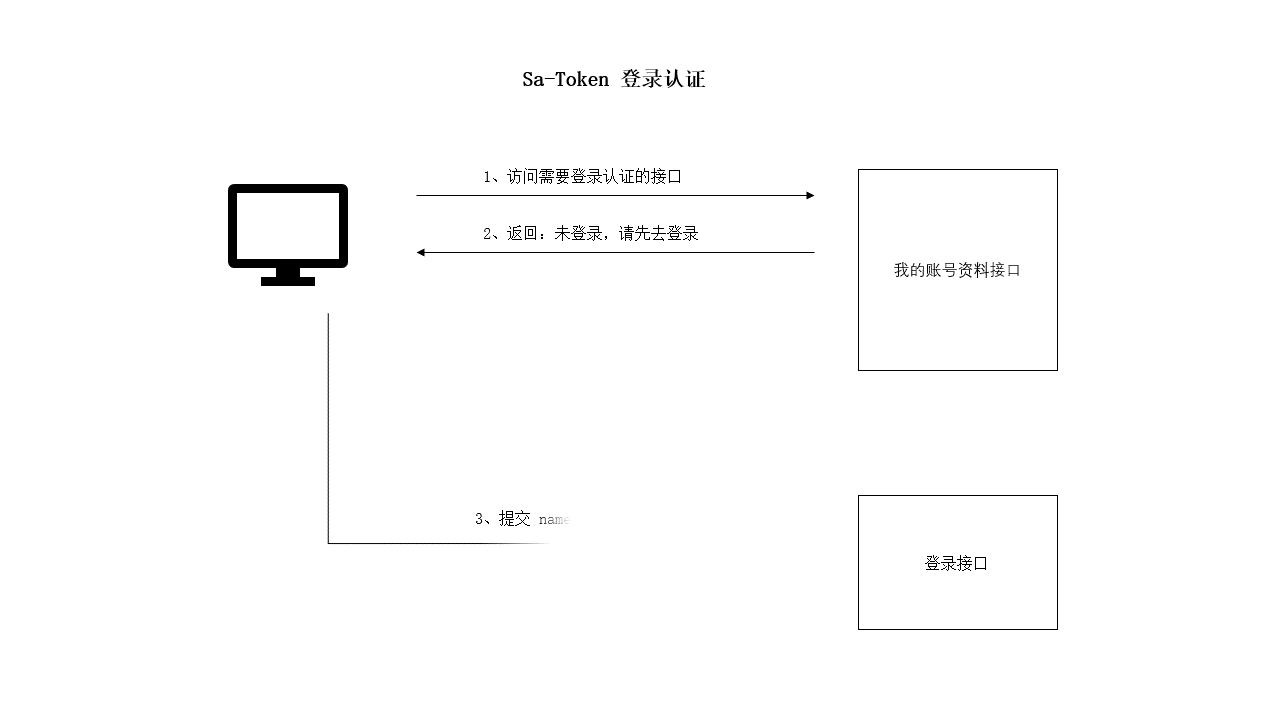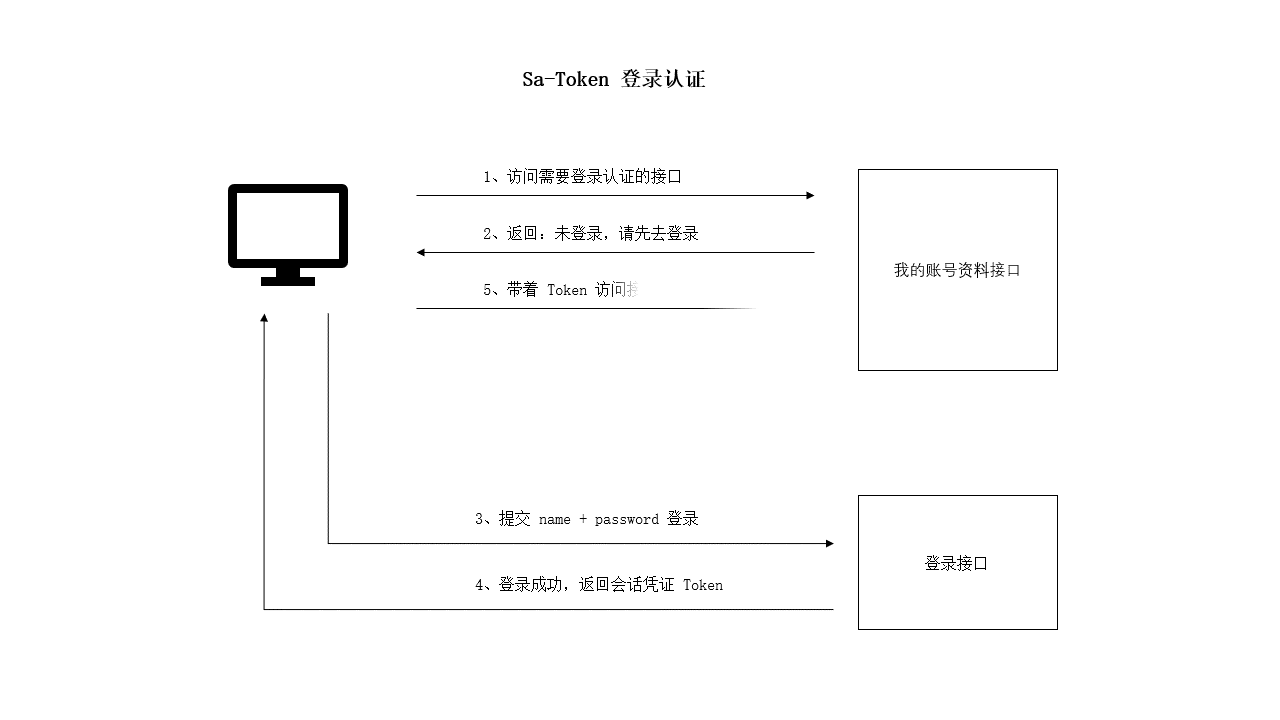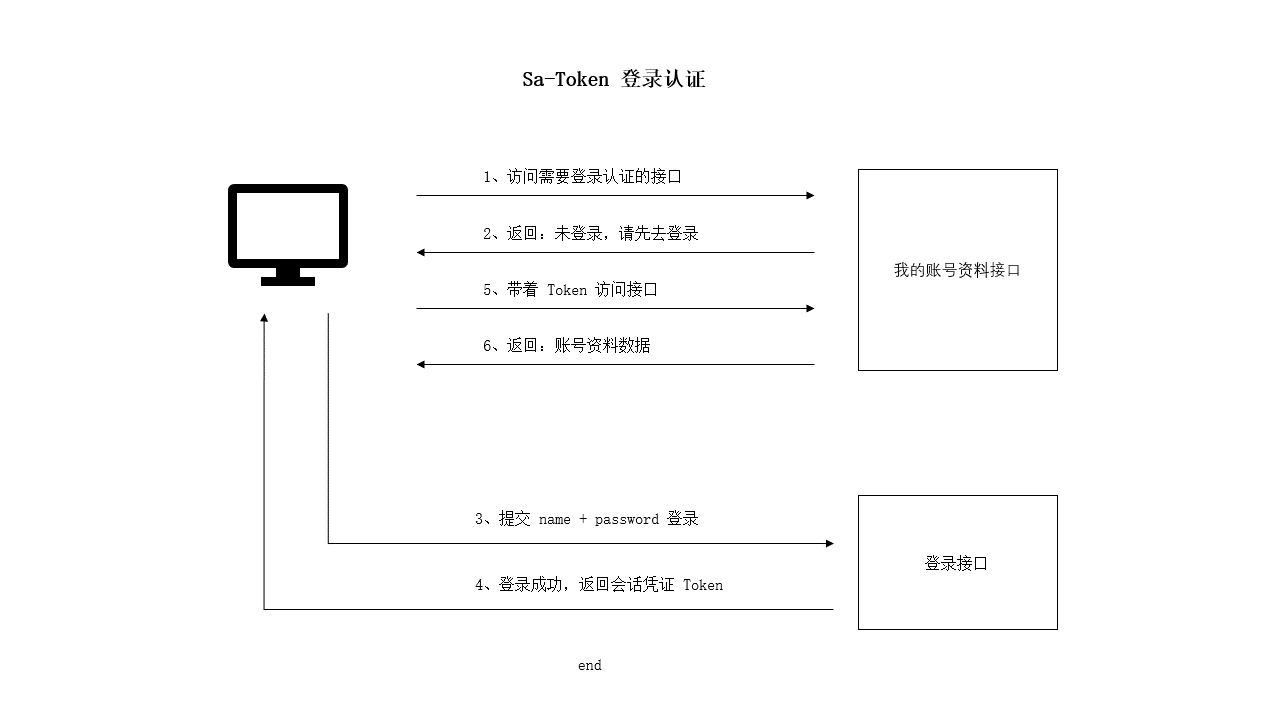
SpringBoot 项目使用 Sa-Token 完成登录认证
一、设计思路 对于一些登录之后才能访问的接口(例如:查询我的账号资料),我们通常的做法是增加一层接口校验: 如果校验通过,则:正常返回数据。如果校验未通过,则:抛出异…...

javaScript 蓝桥杯----梅楼封的一天
目录一、介绍二、目标1.函数入参要求:2.出参要求:三、输出示例1.示例一2.示例二3.示例三4.示例四5.示例五四、待完善代码五、知识点1.正则表达式2.split方法3.test方法4.match方法5.matchAll方法6.slice方法7.replace() 方法8.repeat方法六、答案一、介绍…...

谷粒商城笔记+踩坑(18)——购物车
目录 一、环境搭建 1.1、购物车模块初始化 1.2、动静资源处理 1.3、页面跳转配置 二、数据模型分析 2.1、购物车需求 2.1.1、离线购物车和在线购物车需求、数据库选择redis 2.1.2、购物车数据结构 2.2、模型类抽取,Cart和CartItem 2.3、Redis依赖和配置、…...
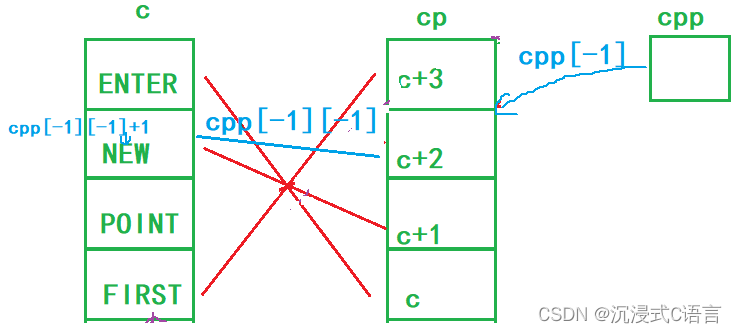
进阶C语言:指针笔试题
在学习完进阶C指针之后,可以来做一些笔试题来进行提升、巩固,小编在这里给大家分享几道比较有意思的笔试题 目录 一、笔试题1: 二、笔试题2 三、笔试题3: 四、笔试题4: 五、笔试题5: 编辑 六、笔试题…...

基于SSM(jsp)的宿舍管理系统
带项目源码和数据库文件 MySQL 导入即可用 可作为毕设参考 框架:SSM 1.1功能需求 本系统的设计目的是为了让老师可以随时随地的关注学生的在校情情况,方便老师对学生在校情况的添加、修改、删除和查询,实时关注学生的安全问题。该系统能…...

Java Web应用开发——作业四
一.单项选择题(共3题,30.0分) 1 如何获取一个 Cookie[]( ) A、 request.getCookies() B、 request.getCookie() C、 response.getCookies() D、 response.getCookie() 正确答案: A 2 ( )隐…...
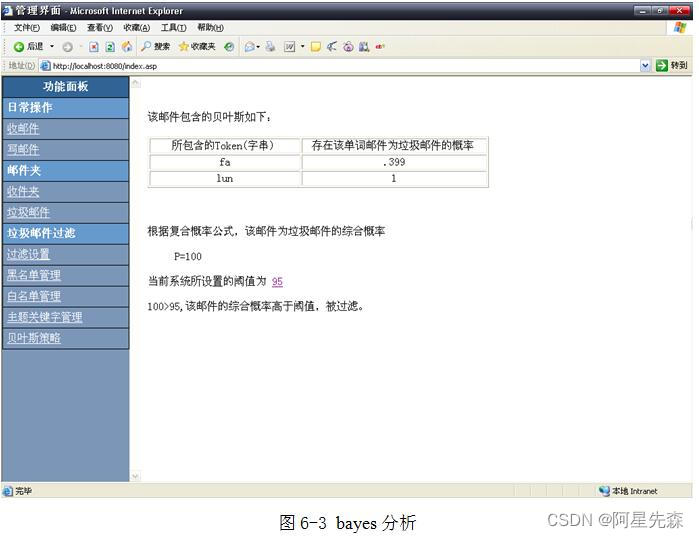
基于ASP的反垃圾邮件管理系统的设计与实现
随着Internet的迅速普及,电子邮件以其快捷、方便、低成本的特点逐渐成为人们进行信息交流的主要媒介之一,但是随之而来的垃圾邮件也越来越泛滥。垃圾邮件占用了有限的存储、计算和网络资源,耗费了用户大量的处理时间,影响和干扰了…...
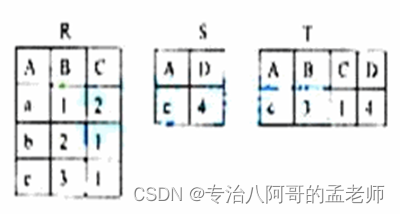
2010年9月计算机二级JAVA笔试试题及答案
一、选择题(每小题2分,共70分) 下列各题A)、B)、C)、D)四个选项中,只有一个选项是正确的。请将正确选项填涂在答题卡相应位置上,答在试卷上不得分。 (1&…...
博客让谷歌或是百度收录
参考以下大佬的博客教程 Hexo框架(六):SEO优化及站点被搜索引擎收录设置 | 你真是一个美好的人类 第一步 安装百度和 Google 的站点地图生成插件: npm install hexo-generator-baidu-sitemap --save npm install hexo-generator-sitemap --save 然后来…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

