人工智能与机器学习原理精解【28】
文章目录
- 随机森林
- 随机森林详解
- 随机森林的详细解释
- 1. 随机森林的基本概念、原理和应用场景、公式和计算
- 2. 随机森林在机器学习、深度学习等领域的重要性
- 3. 实际应用案例及其优势和局限性
- 4. 随机森林在解决实际问题中的价值和意义
- 随机森林局限性的详细归纳
- 随机森林主要的应用领域和具体场景
- 随机森林的算法过程
- 一、随机森林的算法过程
- 二、公式和计算
- 三、随机森林的优缺点
- Bootstrap抽样方法
- Bootstrap抽样方法的基本步骤包括:
- Bootstrap抽样方法的优点:
- Bootstrap抽样方法的局限性:
- 参考文献
随机森林
随机森林详解
随机森林的详细解释
1. 随机森林的基本概念、原理和应用场景、公式和计算
基本概念
随机森林(Random Forest)是一种集成学习方法,通过构建多个决策树(Decision Trees)并将它们的预测结果结合起来,从而提高模型的准确性和稳定性。随机森林可以用于分类和回归任务。
原理
随机森林的核心思想是通过“随机”和“集成”来构建一组决策树,并通过这些树的预测结果来形成最终预测。随机性体现在两个方面:一是数据集的随机选择(通过bootstrap抽样),二是特征选择的随机性。集成则是通过投票或平均的方式将多棵决策树的预测结果结合起来。
- Bootstrap抽样:从原始数据集中随机有放回地抽取子集,用于训练每棵决策树。
- 特征选择:在每个节点分裂时,从所有可用特征中随机选择一个子集,然后在这个子集上选择最优特征进行分裂。
应用场景
随机森林适用于分类和回归问题,广泛应用于金融分析、医疗健康、电子商务推荐系统等领域。例如,用于欺诈检测、垃圾邮件检测、文本情感分析、预测患者风险、房价预测等。
公式和计算
对于分类任务,最终预测结果是通过多数投票法得到的:
y ^ = majority_vote ( h 1 ( x ) , h 2 ( x ) , … , h N ( x ) ) \hat{y} = \text{majority\_vote}(h_1(x), h_2(x), \ldots, h_N(x)) y^=majority_vote(h1(x),h2(x),…,hN(x))
其中, h i ( x ) h_i(x) hi(x)是第 i i i棵决策树对输入 x x x的预测结果。
对于回归任务,最终预测结果是所有树预测结果的平均值:
y ^ = 1 N ∑ i = 1 N h i ( x ) \hat{y} = \frac{1}{N} \sum_{i=1}^{N} h_i(x) y^=N1i=1∑Nhi(x)
其中,( N ) 是决策树的数量。
2. 随机森林在机器学习、深度学习等领域的重要性
在机器学习领域
随机森林作为一种强大的集成学习方法,在机器学习领域具有重要地位。它通过结合多个决策树来克服单个决策树容易过拟合的问题,提高模型的准确性和稳定性。随机森林在处理高维数据、不平衡数据以及缺失值方面表现出色,且易于实现并行化,训练速度较快。
与深度学习的比较
虽然深度学习在处理复杂非线性问题时具有优势,但随机森林在某些方面更为灵活和高效。随机森林不需要复杂的网络结构调参,且对计算资源的要求相对较低。此外,随机森林能够给出特征的重要性评估,这在解释模型预测结果时非常有用。
3. 实际应用案例及其优势和局限性
实际应用案例
- 欺诈检测:在金融领域,随机森林用于识别欺诈交易,通过分析大量交易数据中的模式来预测哪些交易可能是欺诈行为。
- 医学诊断:在临床医学中,随机森林被用于疾病预测和风险评估,通过结合患者的多种临床信息来提高诊断的准确性。
- 房价预测:在房地产领域,随机森林用于预测房价,通过考虑房屋的位置、面积、装修情况等多个因素来给出房价的估计值。
优势
- 高准确性:通过集成多个决策树,随机森林通常比单个决策树更准确。
- 抗过拟合:由于引入了随机性,随机森林能够有效降低过拟合的风险。
- 特征重要性评估:能够方便地衡量每个特征对模型预测结果的重要性。
- 处理高维数据:无需进行复杂的特征选择或降维,可以直接处理高维数据。
局限性
- 计算资源消耗大:构建大量的决策树并集成它们的结果可能需要较多的计算资源。
- 模型可解释性不佳:虽然可以提供特征重要性评分,但整体上随机森林作为一个黑盒模型,其预测过程不如单一决策树那样直观易懂。
- 对参数敏感:模型性能对参数设置(如决策树的数量、特征子集的大小等)较为敏感,需要进行适当的参数调优。
4. 随机森林在解决实际问题中的价值和意义
随机森林在实际问题解决中展现出巨大的价值和意义。它不仅能够提高模型的预测准确性和稳定性,还能够处理复杂的数据集,包括高维数据、不平衡数据以及含有缺失值的数据。此外,随机森林提供的特征重要性评估功能有助于深入理解数据的内在结构和动态,为数据分析和模型优化提供有力支持。通过随机森林,数据科学家和领域专家能够更加准确地把握问题的本质,从而做出更加科学和合理的决策。
随机森林局限性的详细归纳
-
模型可解释性不足:
- 随机森林是一个黑盒模型,其内部决策过程相对复杂,难以直观理解。这导致在需要模型解释性的场合,如医学诊断、法律判决等,随机森林可能不是最佳选择。
- 尽管随机森林可以提供特征重要性评分,但这只是对整个模型贡献的一个大致衡量,并不能详细解释每个决策树的决策过程。
-
参数敏感性和调参困难:
- 随机森林的性能受到多个参数的影响,如决策树的数量、特征子集的大小、树的深度等。不恰当的参数设置可能导致模型性能大幅下降。
- 调参过程通常需要通过交叉验证等方法进行,这增加了模型的复杂性和计算成本。
-
计算资源消耗大:
- 当数据集非常大或特征维度非常高时,构建和训练大量的决策树可能会消耗大量的计算资源和时间。
- 尽管随机森林可以并行训练,但在某些情况下,硬件资源的限制仍然可能成为瓶颈。
-
对噪声和异常值敏感:
- 随机森林在处理包含噪声和异常值的数据时,可能会受到较大影响。这些异常数据可能会导致决策树做出错误的分裂决策,从而降低模型的整体性能。
- 尽管随机森林通过集成多个决策树来降低过拟合的风险,但在极端情况下,噪声和异常值仍然可能对模型产生不利影响。
-
缺乏创新性:
- 随机森林是一种相对成熟的算法,其基本原理和框架已经相对固定。这意味着在算法创新方面,随机森林可能不如一些新兴的深度学习算法具有潜力。
- 然而,这并不意味着随机森林没有应用价值,相反,它在许多实际应用中仍然表现出色。但在需要算法创新和突破的领域,可能需要考虑其他更先进的算法。
-
可能忽视数据中的非线性关系:
- 随机森林基于决策树的分裂规则,通常只能捕捉到数据中的线性或简单非线性关系。对于更复杂的数据结构,如高维空间中的非线性关系,随机森林可能无法充分捕捉。
- 在这种情况下,可能需要考虑使用其他能够处理复杂非线性关系的算法,如深度学习中的神经网络等。
综上所述,尽管随机森林在许多方面表现出色,但仍存在一些局限性。在实际应用中,需要根据具体问题的需求和数据的特性来选择合适的算法,并可能需要对随机森林进行适当的改进或优化以达到最佳效果。
随机森林主要的应用领域和具体场景
-
金融领域:
- 信用评估:利用随机森林分析客户的信用历史、收入情况、负债状况等,以评估客户的信用风险。
- 欺诈检测:通过随机森林识别异常交易模式,及时发现并预防金融欺诈行为。
- 投资决策:结合市场数据、公司财务报表等信息,利用随机森林预测股票价格、市场趋势,辅助投资决策。
-
医疗健康:
- 疾病预测:基于患者的临床数据(如年龄、性别、病史、检查结果等),利用随机森林预测患者患某种疾病的风险。
- 诊断辅助:结合医学影像、生理指标等数据,辅助医生进行疾病诊断,提高诊断准确性。
- 药物研发:在药物筛选、药效评估等阶段,利用随机森林分析大量实验数据,加速药物研发进程。
-
电子商务与零售:
- 商品推荐:基于用户的浏览历史、购买记录、兴趣偏好等,利用随机森林构建个性化推荐系统。
- 库存管理:通过分析销售数据、季节性因素等,预测商品需求,优化库存管理策略。
- 价格优化:利用随机森林分析市场竞争、消费者行为等数据,制定动态定价策略。
-
市场营销:
- 客户细分:基于客户的消费习惯、偏好、价值等,利用随机森林进行客户细分,制定针对性营销策略。
- 响应预测:预测客户对营销活动的响应概率,如购买意愿、参与度等,以优化营销资源配置。
- 广告投放:通过分析用户行为、兴趣等数据,利用随机森林优化广告投放策略,提高广告效果。
-
智能制造与物联网:
- 设备故障预测:结合传感器数据、运行历史等,利用随机森林预测设备故障风险,提前进行维护。
- 生产优化:通过分析生产过程中的各种参数(如温度、压力、速度等),优化生产流程,提高生产效率。
- 质量控制:利用随机森林分析产品质量数据,及时发现并处理质量问题,保障产品质量稳定。
-
环境保护与气候变化:
- 空气质量预测:结合气象数据、污染源信息等,利用随机森林预测空气质量变化,为环保决策提供依据。
- 生态系统评估:通过分析生物多样性、土地利用变化等数据,评估生态系统健康状况,为生态保护提供支持。
- 气候变化研究:利用随机森林分析历史气候数据,预测未来气候变化趋势,为应对气候变化提供科学依据。
综上所述,随机森林在金融、医疗健康、电子商务、市场营销、智能制造、环境保护等多个领域都有广泛的应用场景。其强大的数据处理能力和预测准确性为各领域提供了有力的决策支持。
随机森林的算法过程
一、随机森林的算法过程
随机森林的算法过程可以概括为以下几个步骤:
-
数据集的随机抽样:
- 使用Bootstrap抽样方法从原始数据集中随机有放回地抽取多个样本集,每个样本集的大小与原始数据集相同。这样,每个样本集都可能包含重复的样本,也可能不包含原始数据集中的某些样本。
-
特征的随机选择:
- 对于每个样本集,随机选择一部分特征用于构建决策树。这个特征子集的大小远小于原始特征集的大小,从而增加决策树之间的差异性。
-
构建决策树:
- 使用每个样本集和对应的特征子集构建决策树。在构建过程中,每个节点都基于特征子集中的最佳特征进行分裂,直到满足停止条件(如节点中的样本都属于同一类,或达到预设的树的最大深度等)。
-
集成决策树:
- 重复以上步骤,构建多棵决策树,形成随机森林。对于分类问题,通过投票的方式决定最终的分类结果;对于回归问题,计算所有决策树预测结果的平均值作为最终的预测结果。
二、公式和计算
在随机森林的算法过程中,虽然没有直接的数学公式来描述整个过程,但涉及到一些关键的公式和计算方法:
-
基尼不纯度公式:
- 用于度量样本集的不纯度,即样本集中各类别的分布情况。公式为:
Gini ( U ) = ∑ i = 1 C p ( u i ) ∗ ( 1 − p ( u i ) ) \text{Gini}(U) = \sum_{i=1}^{C} p(ui) * (1 - p(ui)) Gini(U)=i=1∑Cp(ui)∗(1−p(ui))
其中, C C C是类别总数, p ( u i ) p(ui) p(ui)是随机样本属于类别 i i i的概率。
- 用于度量样本集的不纯度,即样本集中各类别的分布情况。公式为:
-
熵公式:
- 与基尼不纯度类似,也是用于度量样本集的混乱程度。公式为:
H ( U ) = − ∑ i = 1 C p ( u i ) ∗ log 2 p ( u i ) \text{H}(U) = - \sum_{i=1}^{C} p(ui) * \log_2 p(ui) H(U)=−i=1∑Cp(ui)∗log2p(ui)
- 与基尼不纯度类似,也是用于度量样本集的混乱程度。公式为:
-
决策树构建过程中的特征选择:
- 在构建决策树时,需要选择最佳特征进行节点分裂。这通常基于基尼不纯度或熵的减少量来选择特征,即选择能够使节点分裂后基尼不纯度或熵最小化的特征。
-
集成结果计算:
- 对于分类问题,通过投票方式集成决策树的结果。具体来说,对于每个测试样本,统计所有决策树对其类别的预测结果,选择票数最多的类别作为最终的预测结果。
- 对于回归问题,计算所有决策树预测结果的平均值作为最终的预测结果。
三、随机森林的优缺点
-
优点:
- 实现简单,泛化能力强。
- 能够处理高维数据,不需要进行复杂的特征选择或降维。
- 对缺失值和异常值有一定的容忍性。
- 能够评估各个特征在分类问题上的重要性。
-
缺点:
- 模型可解释性相对较差,不如单个决策树直观。
- 在某些情况下,对参数设置较为敏感,需要进行适当的调参。
- 当数据集非常大或特征维度非常高时,构建和训练随机森林可能消耗较多的计算资源。
总的来说,随机森林是一种强大且灵活的机器学习算法,通过集成多个决策树来提高模型的准确性和稳定性。其算法过程涉及数据集的随机抽样、特征的随机选择、决策树的构建和集成等步骤,同时涉及到基尼不纯度、熵等关键公式的应用。在实际应用中,需要根据具体问题的需求和数据的特性来选择合适的算法参数和调优策略。
Bootstrap抽样方法
又称为自助法,是一种在统计领域中非常常用的技术。其核心思想是通过从原始数据中随机抽取样本(允许重复抽取同一个数据),来模拟新的样本集,从而估计我们感兴趣的统计量(如平均值、中位数或标准差等)。Bootstrap抽样方法由Bradley Efron于1979年提出,是一种非参数统计方法。
Bootstrap抽样方法的基本步骤包括:
-
收集样本数据:
- 从总体中随机抽取一定数量的样本数据,这些样本数据应当能够代表总体。
-
自助抽样:
- 使用有放回抽样的方法,从原始样本中抽取与原始样本相同大小的样本,组成一个自助样本。这意味着在每次抽样时,原始样本中的每个观测值都有可能被选中,且选中后会被放回原始样本中,以便在下次抽样时再次被选中。
-
重复抽样:
- 重复上述自助抽样的操作多次,通常重复抽样1000次或更多次,以产生足够多的自助样本。这些重复样本称为重新采样的样本。
-
统计量计算:
- 对于每个自助样本,计算感兴趣的统计量,比如平均值、中位数等。统计量可以是均值、中位数、方差等,具体根据问题的需求而定。
-
得到Bootstrap抽样分布:
- 将所有统计量的结果组成一个分布,即为Bootstrap抽样分布。这个分布描述了从原始数据中随机抽取样本时,统计量可能取到的所有可能值及其概率。
-
估计置信区间:
- 通过Bootstrap抽样分布,可以计算所感兴趣的统计量的置信区间,用于估计抽样误差和确定估计的精度。置信区间的计算方法有多种,如百分位数法、偏差校正法等。
Bootstrap抽样方法的优点:
-
灵活性高:
- 不需要对总体分布做出任何假设,适用于各种类型的数据。
-
鲁棒性强:
- 即使数据分布未知或存在异常值,Bootstrap方法也能够给出相对合理的估计。
-
直观易懂:
- 通过生成大量的自助样本,可以直观地展示如何通过抽样变异来理解统计量的不确定性。
Bootstrap抽样方法的局限性:
-
计算量大:
- 由于需要重复抽样和统计量计算,Bootstrap抽样在样本较大时可能需要较长的计算时间。
-
不能改变未知参数估计量的准确性:
- Bootstrap方法只是未知参数估计量的估计,不能改变其本身的准确性。
Bootstrap抽样方法因其简单和强大而广泛应用于科学研究、商业分析、工程问题等多个领域。例如,在经济学中,研究者可以使用Bootstrap方法来修正经济指标的预测;在金融领域,分析师可以利用Bootstrap抽样来评估和管理投资组合的风险。通过Bootstrap方法,研究者可以在不知道总体分布的情况下进行统计推断,从而更准确地理解数据的特性和规律。
参考文献
- 文心一言
相关文章:

人工智能与机器学习原理精解【28】
文章目录 随机森林随机森林详解随机森林的详细解释1. 随机森林的基本概念、原理和应用场景、公式和计算2. 随机森林在机器学习、深度学习等领域的重要性3. 实际应用案例及其优势和局限性4. 随机森林在解决实际问题中的价值和意义 随机森林局限性的详细归纳随机森林主要的应用领…...
)
StarRocks 中如何做到查询超时(QueryTimeout)
背景 本文基于 StarRocks 3.1.7 主要是分析以下两种超时设置的方式: SESSION 级别 SET query_timeout 10;SELECT sleep(20);SQL 级别 select /* SET_VAR(query_timeout10) */ sleep(20); 通过本文的分析大致可以了解到在Starrocks的FE端是如何进行Command的交互以及数据流走…...

Windows 开发工具使用技巧 Visual Studio使用安装和使用技巧 Visual Studio 快捷键
一、Visual Studio配置详解 1. 安装 Visual Studio 安装时,选择你所需要的组件和工作负载。Visual Studio 提供多种工作负载,例如: ASP.NET 和 Web 开发:用于 Web 应用的开发。 桌面开发(使用 .NET 或 C)…...

计算机网络-系分(5)
目录 计算机网络 DNS解析 DHCP动态主机配置协议 网络规划与设计 层次化网络设计 网络冗余设计 综合布线系统 1. 双栈技术 2. 隧道技术 3. 协议转换技术 其他网络技术 DAS(Direct Attached Storage,直连存储) NAS(Net…...

React Native使用高德地图
在React Native项目中使用高德地图,主要涉及到几个关键步骤:安装高德地图相关的React Native模块、配置项目、申请高德地图API Key、以及在实际组件中使用高德地图功能。以下是一个详细的步骤指南: 一、安装高德地图React Native模块 首先&…...

排序算法的理解
排序算法借鉴了数学里面的不等式的思想 计算机不能直接继承不等式的传递性特征,这个时候才用递归调用去人为的分成不同的部分。或者说,一部分已经大致排序好的数放在一边,另外一边再排。 这是由于计算机只能两两比较数字才会出现的情况。它…...

Yocto - 使用Yocto开发嵌入式Linux系统_04 使用Toaster来创建一个image
Using Toaster to Bake an Image 既然我们已经知道了如何在 Poky 中使用 BitBake 构建图像,那么接下来我们就来学习如何使用 Toaster 构建图像。我们将重点介绍 Toaster 最直接的使用方法,并介绍它的其他功能,让你了解它的能力。 Now that we…...

【C#生态园】后端服务与网络库:选择适合你游戏开发的利器
网络通信不再难题:六种常用游戏开发网络库详解 前言 随着网络游戏行业的蓬勃发展,对于实时多玩家游戏服务和网络通信库的需求也日益增长。在游戏开发中,选择合适的后端服务和网络库可以极大地影响游戏的性能、稳定性和用户体验。本文将介绍…...

计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-09-30
计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-09-30 目录 文章目录 计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-09-30目录1. Proof Automation with Large Language Models概览:论文研究背景:技术挑战:如何破局…...

【漏洞复现】JeecgBoot 积木报表 queryFieldBySql sql注入漏洞
》》》产品描述《《《 积木报表,是一款免费的企业级Web报表工具,像搭建积木一样在线设计报表!功能涵盖,数据报表、打印设计、图表报表、大屏设计等! 》》》漏洞描述《《《 JeecgBoot 积木报表 queryFieldBySq| 接口存在一个 SQL 注入漏洞&…...

Qt6 中相对于 Qt5 的新增特性及亮点
Qt 是一个领先的跨平台应用开发框架,涵盖了桌面、移动、嵌入式等多个平台。随着 Qt6 的发布,Qt 框架经历了重大升级和变革,带来了大量新特性和架构上的改进,使开发者可以更高效地开发现代化应用程序。本文将重点讨论 Qt6 相对于 Q…...

超轻巧modbus调试助手使用说明
一、使用说明 1.1 数据格式 和其他的modbus采集工具一样,本组件也支持各种数据格式,其实就是高字节低字节的顺序。一般是2字节表示一个数据,后面又有4字节表示一个数据,目前好像还有8字节表示一个数据的设备。不同厂家的设备对应…...

Percona Monitoring and Management
Percona Monitoring and Management (PMM)是一款开源的专用于管理和监控MySQL、MongoDB、PostgreSQL...

WarehouseController
目录 1、 WarehouseController 1.1、 //仓库信息设置 1.2、 /// 查询 1.3、 /// 删除 WarehouseController using QXQPS.Models; using QXQPS.Vo; using System; using System.Collections.Generic; using System.Linq; using System.Web; using System.Web.Mv…...

基于 STM32 单片机的温室物理无害生长系统
摘要 : 本系统主要由六大部分组成,分别为 STM32单片机控制模块、温湿度检测模块、风扇、臭氧消毒、温室补光灯、水利灌溉通道等基本设施。单片机可以通过 MOS 管这类的电力电子器件来实现对某些大功率设施的控制如温室内风扇通风系统、温室内定时补光、根据土壤温湿检测来进行…...

新版pycharm如何导入自定义环境
我们新的版本的pycharm的ui更改了,但是我不会导入新的环境了 我们先点击右上角的add interpreter 然后点击添加本地编译器 先导入这个bat文件 再点击load 我们就可以选择我们需要的环境了...

一文彻底搞懂多模态 - 多模态理解+视觉大模型+多模态检索
文章目录 技术交流多模态理解一、图像描述1. 基于编码器-解码器的方法2. 基于注意力机制的方法3. 基于生成对抗网络的方法 二、视频描述三、视觉问答 视觉大模型一、通用图像理解模型二、通用图像生成模型 多模态检索一、单模态检索二、多模态检索三、跨模态检索 最近这一两周看…...

提升效率的编程世界探索与体验
--- 在如今这个信息爆炸、竞争激烈的时代,工作效率对于程序员来说显得尤为重要。为了在日益繁忙的工作环境中脱颖而出,选择合适的编程工具成为了一个关键的决定。不同的工具各有其优势,有的擅长简化代码编写,有的则擅长自动化任…...

VMware tools菜单为灰色无法安装
这个工具之前为灰色,无法安装,导致无法实现跟主机的共享文件夹等操作。极为不便。 根据其他教程提示:看到软件是这个配置。 修改为自动检测,tools就可以安装了。之前没注意到。 也有说dvd光盘也要设置。但是经过我测试。只设置软…...
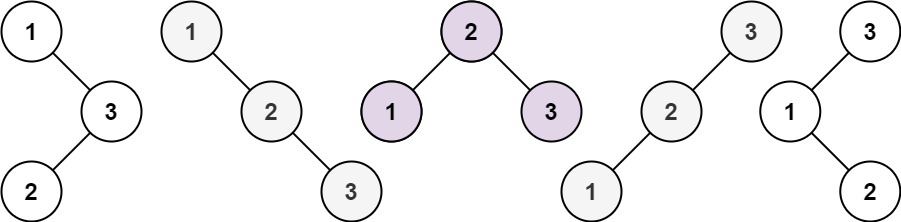
不相同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n 3 输出:5示例 2: 输入:n 1 输出:1提…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

【堆垛策略】设计方法
堆垛策略的设计是积木堆叠系统的核心,直接影响堆叠的稳定性、效率和容错能力。以下是分层次的堆垛策略设计方法,涵盖基础规则、优化算法和容错机制: 1. 基础堆垛规则 (1) 物理稳定性优先 重心原则: 大尺寸/重量积木在下…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
