当前位置： 首页 > news >正文

第九篇——数列和级数(二)：传销骗局的数学原理

news 2026/2/7 22:17:55

目录

  • 一、背景介绍
  • 二、思路&方案
  • 三、过程
    • 1.思维导图
    • 2.文章中经典的句子理解
    • 3.学习之后对于投资市场的理解
    • 4.通过这篇文章结合我知道的东西我能想到什么？
  • 四、总结
  • 五、升华

一、背景介绍

文章不长，但是道理深刻；相邻两个数的差值，决定了发展是无穷大还是无穷小；以及它在生活工作中的运用

二、思路&方案

  • 1.思维导图
  • 2.文章中经典的句子理解
  • 3.学习之后对于投资市场的理解
  • 4.通过这篇文章结合我知道的东西我能想到什么？

三、过程

1.思维导图

2.文章中经典的句子理解

  • 2.1.数列的求和，也就是所谓的级数
  • 2.2.老鼠仓的例子，很多人误以为只要从无限多的人身上挣钱，就能挣很多钱，这其实是不了解级数这个概念而产生的误解
  • 2.3.不仅仅是媒体，任何一个产品，要想成为爆款，都需要提升转发率P这个比例，也就是大家使用后满意，然后愿意主动宣传的比例

3.学习之后对于投资市场的理解

消息的发酵，会是踩踏和延迟的；再加上卡尼曼前景理论；上升的踩踏和下降的踩踏同样强烈；这就也是马太效应

4.通过这篇文章结合我知道的东西我能想到什么？

  • 1.从数学的视角，我们可以明辨很多东西，按道理办事，按逻辑办事
  • 2.任何事情，为别人着想是底层的逻辑

四、总结

  • 1.这个世界有多大，多宽广；你可以从数学视角去体会一下
  • 2.任何道理，都需要讲道理，讲逻辑

五、升华

数学是所有学科的顶层抽象；金融是所有行业的顶层智慧。
在这里插入图片描述

来自得到app中，吴军老师《数学通识50讲》详读总结

相关文章：

第九篇——数列和级数(二)：传销骗局的数学原理

目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么？ 四、总结五、升华 一、背景介绍 文章不长，但是道理深刻；相邻两个数的差值&#xf…...

编程日记 2024/10/3 0:48:39

docker如何查看容器的ip

要查看Docker容器的IP地址&#xff0c;可以使用以下几种方法&#xff1a; 使用docker inspect命令&#xff1a; docker inspect -f {{range .NetworkSettings.Networks}}{{.IPAddress}}{{end}} <容器ID或名称> 使用docker ps和docker inspect组合&#xff1a; 首先查看正…...

编程日记 2024/10/3 0:47:38

Mysql ONLY_FULL_GROUP_BY模式详解、group by非查询字段报错

文章目录 一、问题报错二、ONLY_FULL_GROUP_BY模式2.1、什么是ONLY_FULL_GROUP_BY&#xff1f;2.2、为什么要使用ONLY_FULL_GROUP_BY&#xff1f;2.3、查看sql_mode 三、解决方法3.1、关闭only_full_group_by模式3.1.1、方法一&#xff1a;关闭当前会话中的only_full_group_by3…...

编程日记 2024/10/3 0:45:35

设计模式（2）工厂模式

让一个工厂类去生产出对象 &#xff08;new &#xff09;来。 我们想要一个 形状&#xff0c;我们用工厂去生产出&#xff0c;圆形&#xff0c;方形。 package com.example.factory2;public interface Shape {void draw(); }public class Square implements Shape {Overridep…...

编程日记 2024/10/3 0:44:34

二分查找算法专题（1）

找往期文章包括但不限于本期文章中不懂的知识点&#xff1a; 个人主页&#xff1a;我要学编程(ಥ_ಥ)-CSDN博客 所属专栏&#xff1a; 优选算法专题 目录 二分查找算法的介绍 704. 二分查找 34. 在排序数组中查找元素的第一个和 最后一个位置 35. 搜索插入位置 69. x的平…...

编程日记 2024/10/3 0:40:31

ACP科普：SoS不是救命

Scrum of Scrums&#xff08;SoS&#xff09;是一种用于协调多个Scrum团队之间工作的扩展框架&#xff0c;特别适用于大型项目或组织中有多个团队同时进行开发的情况。它帮助团队在保持敏捷性的同时&#xff0c;解决跨团队的依赖和协调问题。以下是对Scrum of Scrums的详细介绍…...

编程日记 2024/10/3 0:39:30

C++：模拟实现vector

目录 成员变量与迭代器 size capacity empty 迭代器有关函数 实现默认成员函数的前置准备 reserve ​编辑 ​编辑 push_back 构造函数 无参构造 迭代器区间构造 n个val来进行构造 析构函数 拷贝构造函数 赋值重载 增删查改 clear resize pop_back inser…...

编程日记 2024/10/3 0:38:29

Leecode SQL 184. Department Highest Salary 找出tie

Department Highest Salary 注意&#xff01;要找出 tie 的 highest salary&#xff01; Write a solution to find employees who have the highest salary in each of the departments. Return the result table in any order. The result format is in the following ex…...

编程日记 2024/10/3 0:31:23

[Redis][典型运用][缓存]详细讲解

目录 0.什么是缓存&#xff1f;1.使用Redis作为缓存1.为什么用&#xff1f;2.如何用&#xff1f; 2.缓存的更新策略0.前言1.定期生成2.实时生成 3.缓存相关问题1.缓存预热(Cache Preheating)2.缓存穿透(Cache Penetration)3.缓存雪崩(Cache Avalanche)4.缓存击穿(Cache Breakdo…...

编程日记 2024/10/3 0:29:21

GPG error golang 1.19

1. 问题描述及原因分析 在飞腾2000的服务器&#xff0c;OS为Kylin Linux Advanced Server release V10环境下&#xff0c;docker版本为18.09.0&#xff08;docker-engine-18.09.0-101.ky10.aarch64&#xff09;&#xff0c;基于容器镜像golang:1.19编译新的容器镜像&#xff0…...

编程日记 2024/10/3 0:27:19

Linux如何查看每个文件及文件夹的大小

查看当前目录下每个文件夹的大小&#xff0c;包括其内部所有文件&#xff1a; du -sh *-s&#xff1a;仅显示每个文件夹的总大小&#xff0c;而不是每个文件。-h&#xff1a;以人类可读的格式显示。...

编程日记 2024/10/3 0:26:18

Word样式的同步与重置

有时候我们需要修改Word中的样式&#xff0c;实现排版的个性化。 如何同步样式到其他电脑上&#xff1f; Word中的样式是由Normal.dotm文件控制的&#xff0c;对样式所有的设置和修改&#xff0c;都会保存到这个问题件中&#xff0c;所以我们只需要在设置好样式以后&#xff…...

编程日记 2024/10/3 0:25:17

力扣 —— 跳跃游戏

题目一(中等) 给你一个非负整数数组 nums &#xff0c;你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标&#xff0c;如果可以&#xff0c;返回 true &#xff1b;否则&#xff0c;返回 false 。 示例 1&…...

编程日记 2024/10/3 0:22:14

SOCKS5代理和HTTP代理哪个快？深度解析两者的速度差异

在现代互联网环境中&#xff0c;使用代理IP已经成为了许多人日常生活和工作的必备工具。无论是为了保护隐私&#xff0c;还是为了访问某些特定资源&#xff0c;代理IP都扮演着重要的角色。今天&#xff0c;我们就来聊聊SOCKS5代理和HTTP代理&#xff0c;看看这两者到底哪个更快…...

编程日记 2024/10/3 0:21:13

工具介绍---效率高+实用

Visual Studio Code (VS Code) 功能特点&#xff1a; 智能代码提示&#xff1a;内置的智能代码提示功能可以自动完成函数、变量等的输入&#xff0c;提高代码编写速度。插件丰富&#xff1a;支持成千上万的扩展插件&#xff0c;例如代码片段、主题、Linting等&#xff0c;能够…...

编程日记 2024/10/3 0:20:12

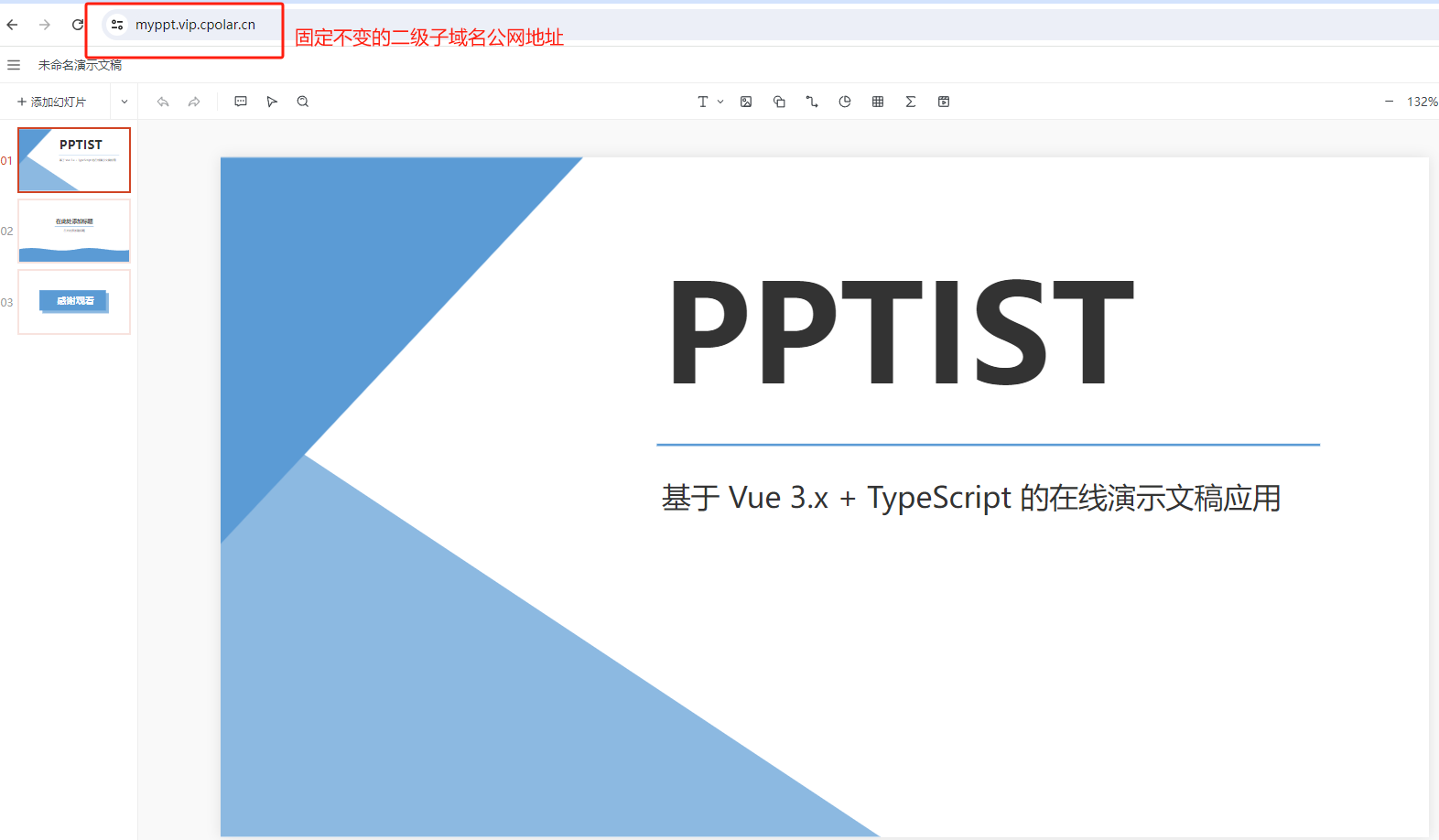
本地部署开源在线PPT制作与演示应用PPTist并实现异地远程使用

文章目录 前言1. 本地安装PPTist2. PPTist 使用介绍3. 安装Cpolar内网穿透4. 配置公网地址5. 配置固定公网地址 前言 本文主要介绍如何在Windows系统环境本地部署开源在线演示文稿应用PPTist&#xff0c;并结合cpolar内网穿透工具实现随时随地远程访问与使用该项目。 PPTist …...

编程日记 2024/10/3 0:15:08

leetcode_238:除自身以外数组的乘积

给你一个整数数组 nums&#xff0c;返回 数组 answer &#xff0c;其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法&#xff0c;且在 O(n) 时间复杂…...

编程日记 2024/10/3 0:13:06

网络协议详解--IPv6

IPv6产生背景 &#xff08;1&#xff09;地址空间的耗尽&#xff1a;因特网呈指数级发展&#xff0c;导致IPv4地址空间几乎耗尽。虽然采用了子网划分、CIDR和NAT地址转换技术&#xff0c;但这没有从根源解决地址耗尽的问题 &#xff08;2&#xff09;IP层安全需求的增长&#x…...

编程日记 2024/10/3 0:10:03

阿里云域名注册购买和备案

文章目录 1、阿里云首页搜索 域名注册2、点击 控制台3、域名控制台 1、阿里云首页搜索 域名注册 2、点击 控制台 3、域名控制台...

编程日记 2024/10/3 0:09:02

【经典机器学习算法】谱聚类算法及其实现（python）

&#x1f308; 个人主页&#xff1a;十二月的猫-CSDN博客 &#x1f525; 系列专栏&#xff1a; &#x1f3c0;深度学习_十二月的猫的博客-CSDN博客 &#x1f4aa;&#x1f3fb; 十二月的寒冬阻挡不了春天的脚步&#xff0c;十二点的黑夜遮蔽不住黎明的曙光 目录 1. 前言 2. 前…...

编程日记 2024/10/3 0:08:01

MPNet：旋转机械轻量化故障诊断模型详解python代码复现

目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块（MBFM） 2.2 残差注意力金字塔模块（RAPM） 2.2.1 空间金字塔注意力（SPA） 2.2.2 金字塔残差块（PRBlock） 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

编程新知 2026/2/7 5:16:28

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2026/2/6 23:18:59

高等数学（下）题型笔记（八）空间解析几何与向量代数

目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

编程新知 2026/1/28 9:04:29

【配置 YOLOX 用于按目录分类的图片数据集】

现在的图标点选越来越多&#xff0c;如何一步解决&#xff0c;采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集&#xff08;每个目录代表一个类别&#xff0c;目录下是该类别的所有图片&#xff09;&#xff0c;你需要进行以下配置步骤&#x…...

编程新知 2026/1/30 4:52:56

相机Camera日志分析之三十一：高通Camx HAL十种流程基础分析关键字汇总（后续持续更新中）

【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了：有对最普通的场景进行各个日志注释讲解，但相机场景太多，日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志，通过下列分类关键字搜索，即可清晰的分析不同场景的相机运行流程差异…...

编程新知 2025/11/20 7:13:43

uniapp中使用aixos 报错

问题&#xff1a; 在uniapp中使用aixos&#xff0c;运行后报如下错误&#xff1a; AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

编程新知 2025/11/29 21:26:48

Java面试专项一-准备篇

一、企业简历筛选规则 一般企业的简历筛选流程&#xff1a;首先由HR先筛选一部分简历后&#xff0c;在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如&#xff1a;Boss直聘&#xff08;招聘方平台&#xff09; 直接按照条件进行筛选 例如&#xff1a…...

编程新知 2026/1/26 19:10:48

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容

目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法&#xff0c;当前调用一个医疗行业的AI识别算法后返回…...

编程新知 2026/1/20 22:45:38

CSS设置元素的宽度根据其内容自动调整

width: fit-content 是 CSS 中的一个属性值&#xff0c;用于设置元素的宽度根据其内容自动调整&#xff0c;确保宽度刚好容纳内容而不会超出。 效果对比 默认情况&#xff08;width: auto&#xff09;&#xff1a; 块级元素&#xff08;如 <div>&#xff09;会占满父容器…...

编程新知 2025/10/16 16:03:09

DiscuzX3.5发帖json api

参考文章&#xff1a;PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下&#xff0c;适配我自己的需求 有一个站点存在多个采集站&#xff0c;我想通过主站拿标题&#xff0c;采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

编程新知 2025/11/25 17:20:50