python 实现点的多项式算法
点的多项式算法介绍
点的多项式算法通常指的是通过一组点(即数据点,通常包括自变量和因变量的值)来拟合一个多项式函数的方法。这种方法在数值分析、统计学、机器学习等领域中非常常见。下面是一些常见的多项式拟合算法:
1. 最小二乘法
最小二乘法是最常用的多项式拟合方法。它通过最小化误差的平方和(即残差平方和)来找到最佳的拟合多项式。具体步骤如下:
选择多项式的阶数:首先,你需要决定使用多少阶的多项式来拟合数据。阶数越高,多项式可能越能精确地通过每个数据点,但也可能导致过拟合。
建立方程组:对于给定的数据点 ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) (x_1,y_1),(x_2,y_2),…,(x_n,y_n) (x1,y1),(x2,y2),…,(xn,yn) 和一个 𝑚 阶多项式 p ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a m x m p(x)=a_0+a_1x+a_2x^2+⋯+a_mx^m p(x)=a0+a1x+a2x2+⋯+amxm,你可以为每个数据点建立一个方程,即 p ( x i ) = y i p(x_i)=y_i p(xi)=yi。然而,由于数据点通常不会完美地落在多项式上,你需要最小化残差 r i = p ( x i ) − y i r_i=p(x_i)−y_i ri=p(xi)−yi 的平方和。
解方程组:将残差平方和 S = ∑ i = 1 n r i 2 S=\sum_{i=1}^nr_i^2 S=∑i=1nri2最小化,通过求偏导数并令其为零,可以得到一个线性方程组,该方程组包含多项式系数 a 0 , a 1 , … , a m a_0,a_1,…,a_m a0,a1,…,am 作为未知数。
求解:解这个线性方程组,得到多项式的系数。
2. 数值方法
除了最小二乘法,还可以使用一些数值方法来求解多项式系数,如梯度下降法、牛顿法等。这些方法通过迭代地调整系数来最小化残差平方和。
3. 软件工具
在实际应用中,通常会使用专门的软件或库来执行多项式拟合,如Python的NumPy、SciPy、Matplotlib(通过NumPy的polyfit函数)或MATLAB的polyfit函数等。这些工具提供了方便的函数和接口,让用户可以轻松地拟合多项式并获取系数。
示例(Python)
使用NumPy的polyfit函数进行多项式拟合的示例:
import numpy as np
import matplotlib.pyplot as plt# 示例数据
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 0.8, 0.9, 0.1, -0.8, -1])# 拟合2阶多项式
coefficients = np.polyfit(x, y, 2)
polynomial = np.poly1d(coefficients)# 打印多项式系数
print(polynomial)# 绘制原始数据点和拟合曲线
xp = np.linspace(0, 5, 100)
plt.plot(x, y, 'o', xp, polynomial(xp), '-')
plt.show()
这段代码将拟合一个2阶多项式,并绘制原始数据点和拟合的曲线。
点的多项式算法python实现样例
下面是一个Python实现的多项式算法示例:
class Polynomial:def __init__(self, coefficients):self.coefficients = coefficientsdef __str__(self):terms = []degree = len(self.coefficients) - 1for i, coeff in enumerate(self.coefficients):if coeff != 0:if i < degree:terms.append(f"{coeff}x^{degree-i}")else:terms.append(str(coeff))return ' + '.join(terms)def __add__(self, other):if len(self.coefficients) > len(other.coefficients):longer = selfshorter = otherelse:longer = othershorter = selfresult = []for i in range(len(longer.coefficients)):if i < len(shorter.coefficients):result.append(longer.coefficients[i] + shorter.coefficients[i])else:result.append(longer.coefficients[i])return Polynomial(result)def __sub__(self, other):neg_other = Polynomial([-coeff for coeff in other.coefficients])return self.__add__(neg_other)def __mul__(self, other):result = [0] * (len(self.coefficients) + len(other.coefficients) - 1)for i in range(len(self.coefficients)):for j in range(len(other.coefficients)):result[i+j] += self.coefficients[i] * other.coefficients[j]return Polynomial(result)def evaluate(self, x):result = 0for i, coeff in enumerate(self.coefficients):result += coeff * (x ** (len(self.coefficients) - i - 1))return result# 示例用法
poly1 = Polynomial([1, 0, 2]) # 2x^2 + 1
poly2 = Polynomial([3, -1]) # -x + 3add_result = poly1 + poly2
sub_result = poly1 - poly2
mul_result = poly1 * poly2print(f"poly1: {poly1}") # 输出:poly1: 2x^2 + 1
print(f"poly2: {poly2}") # 输出:poly2: -x + 3
print(f"poly1 + poly2: {add_result}") # 输出:poly1 + poly2: 2x^2 - x + 4
print(f"poly1 - poly2: {sub_result}") # 输出:poly1 - poly2: 2x^2 + x - 2
print(f"poly1 * poly2: {mul_result}") # 输出:poly1 * poly2: -3x^3 + 6x^2 - x + 3print(f"poly1(2): {poly1.evaluate(2)}") # 输出:poly1(2): 9
这个示例中,Polynomial类实现了多项式的基本操作,包括加法、减法、乘法和求值。coefficients变量存储多项式的系数。__str__方法将多项式转换为可读字符串形式。__add__、__sub__和__mul__方法实现了多项式的加法、减法和乘法。evaluate方法用于求多项式在给定值下的结果。
示例使用了两个多项式poly1和poly2进行加法、减法和乘法操作,并计算了poly1在x=2处的值。
输出结果为:
poly1: 2x^2 + 1
poly2: -x + 3
poly1 + poly2: 2x^2 - x + 4
poly1 - poly2: 2x^2 + x - 2
poly1 * poly2: -3x^3 + 6x^2 - x + 3
poly1(2): 9
相关文章:

python 实现点的多项式算法
点的多项式算法介绍 点的多项式算法通常指的是通过一组点(即数据点,通常包括自变量和因变量的值)来拟合一个多项式函数的方法。这种方法在数值分析、统计学、机器学习等领域中非常常见。下面是一些常见的多项式拟合算法: 1. 最小…...
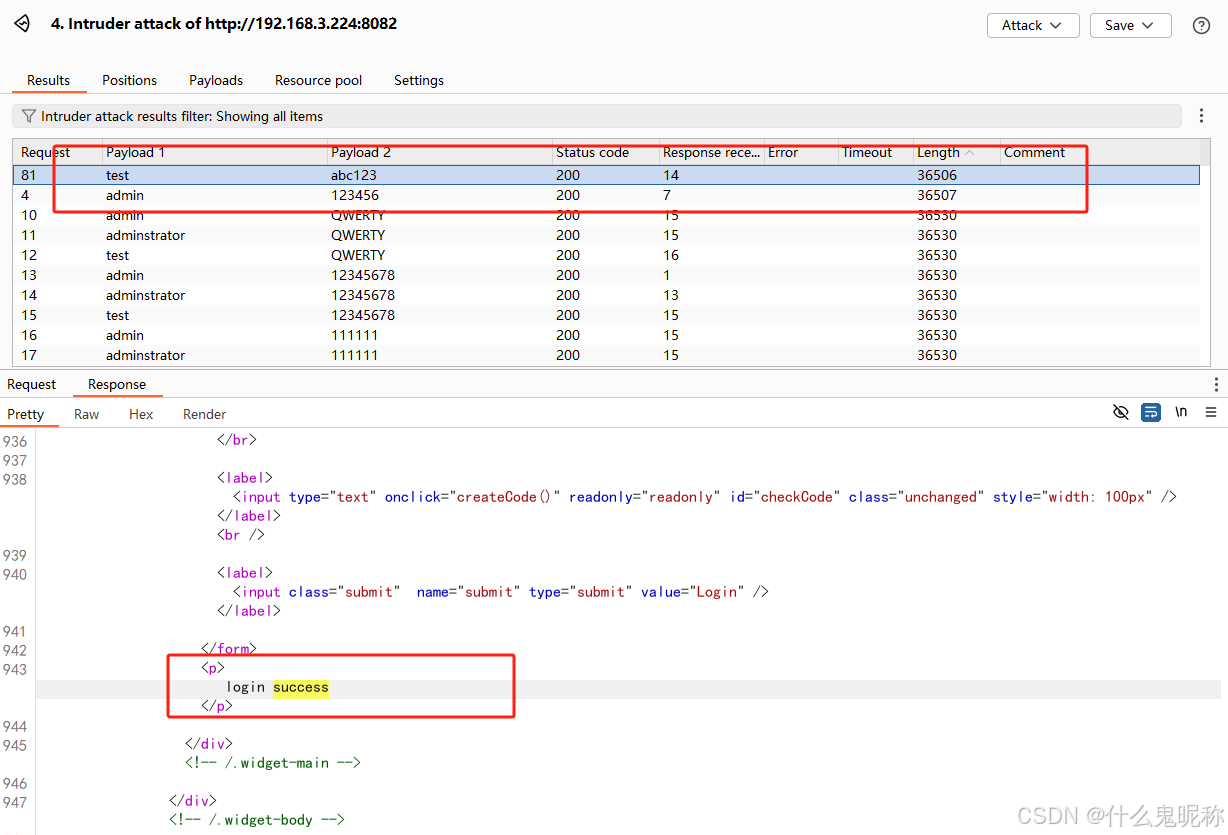
Pikachu-暴力破解-验证码绕过(on client)
访问页面, 从burpsuite 上看到返回的源代码; 验证码生成时通过 createCode 方法生成,在前端页面生成; 同时也是在前端做的校验; 直接验证;F12 -- 网络,随便输入个账号、密码、验证码࿰…...

【Spring】Bean 的生命周期:从实例化到销毁
实例化阶段: Bean的实例化是通过反射创建的。Spring根据Component、Bean或者XML中的<bean>元素配置,来确定要创建的Bean。 属性赋值阶段: 实例化完成后,Spring会进行依赖注入。包括将属性值注入到Bean的字段中,…...
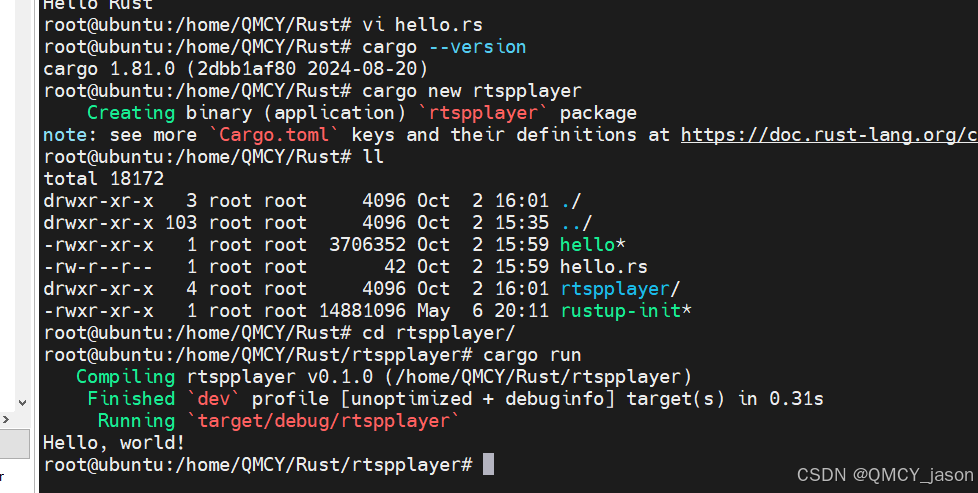
Ubuntu 安装RUST
官方给的是这样如下脚本 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh 太慢了 curl --proto https --tlsv1.2 -sSf https://sh.rustup.rs | sh -x 执行这个脚本后会给出对应的下载链接 如下图 我直接给出来 大多数应该都是这个 https://static.rust-…...

Android Compose的基本使用
前言: Compose这个东西呢,好处我没发现,坏处就是学习成本和低版本兼容. 不过,看在官方力推的份儿上,有空就学一下吧. 当初的kotlin,很多人说鸡肋(包括我)!现在不也咔咔用纯kotlin做项目吗?哈哈哈哈. 未来的事情,谁说得清呢? 首先创建一个专用的Compose项目 对没错!看到E…...
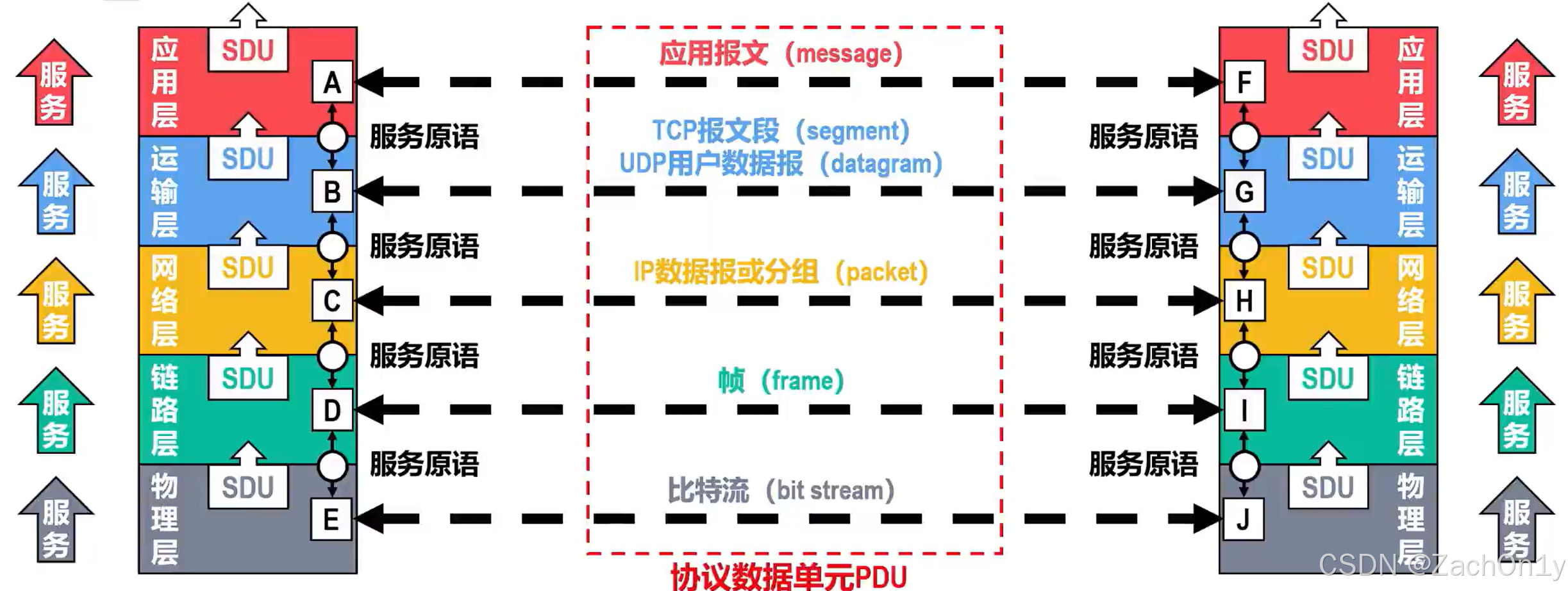
计算机网络:计算机网络体系结构 —— 专用术语总结
文章目录 专用术语实体协议服务服务访问点 SAP 服务原语 SP 协议数据单元 PDU服务数据单元 SDU 专用术语 实体 实体是指任何可以发送或接收信息的硬件或软件进程 对等实体是指通信双方处于相同层次中的实体,如通信双方应用层的浏览器进程和 Web 服务器进程。 协…...
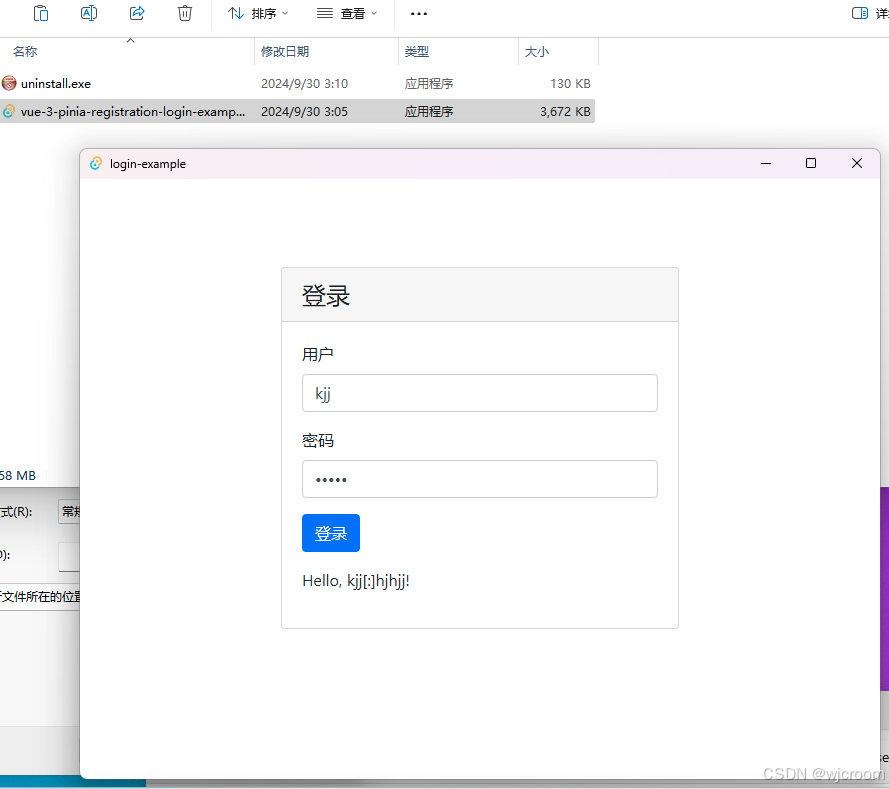
Rust的前端Tauri编程-基于JS框架的初步探索
上次的项目做完后,有一项遗憾,没有返回结果,而结果是一个html表格,我想用html直接在窗口显示,这时发现R里面包括slint没有很直接的方法,直接弹出浏览器有点太简单没有挑战。这是就被推送了他的竞争对手&…...
【Flume Kafaka实战】Using Kafka with Flume
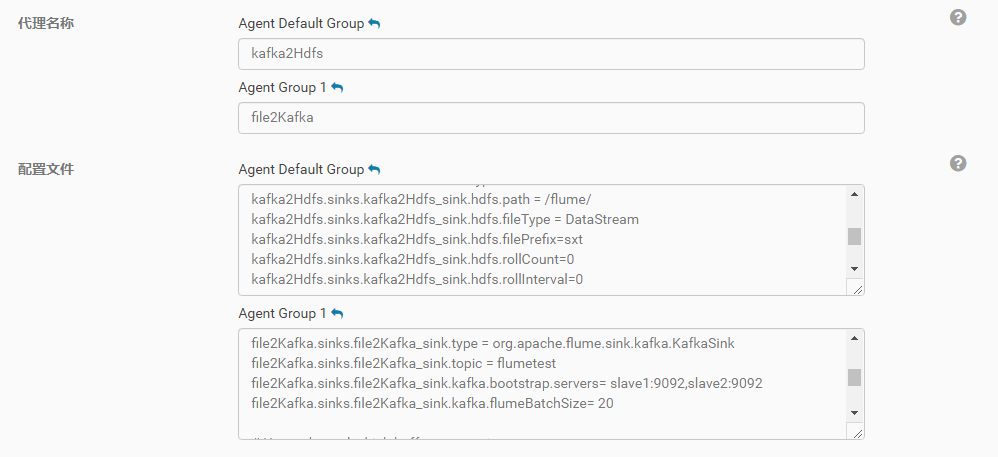
一 目标 在Cloudera Manager中创建两个Flume的Agent,Agent1从local file中获取内容,写入到kafka的队列中。Agent2以Agent1的sink作为source,将数据从kafka中读取出来,写入到HDFS中。 二 实战 2.1 Kafka Sink 第一步࿰…...
5G NR物理信号
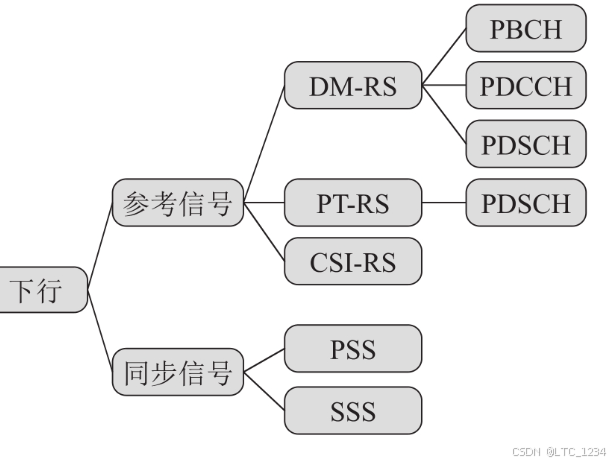
文章目录 NR 物理信号与LTE的区别上行参考信号DMRS (UL)SRSPT-RS(UL) 下行参考信号DMRS(DL)PT-RS(DL)CSI-RSPSSSSS NR 物理信号与LTE的区别 用SSS、CSI-RS和DMRS 取代了CRS信号。下行业务信道采用TM1波束赋形传输模式。基于SSB 或者CSI-RS进行RSRP和SINR测量。基于DMRS 进行共…...
Pikachu-Cross-Site Scripting-存储型xss
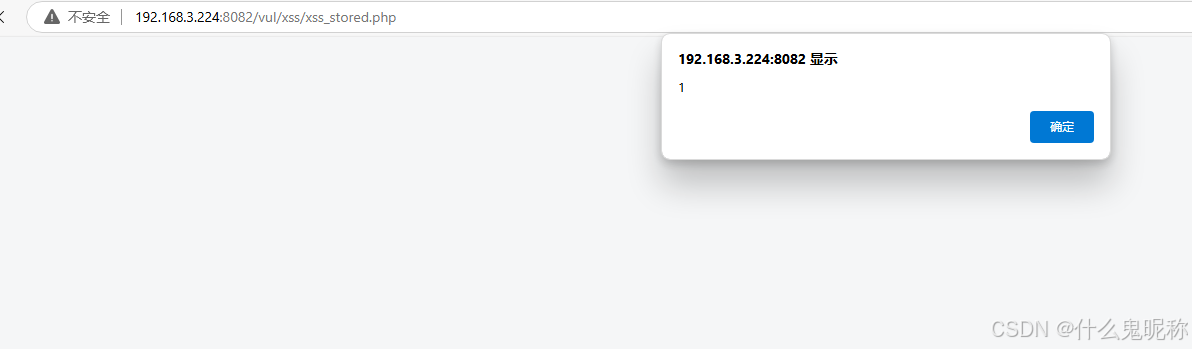
存储型xss ,随便输入点内容,都能保存下来;刷新后也不会丢失;输入特殊字符,也能原样返回; 查看代码,也可以看到输出结果直接原路返回,不做处理 构造payload <script>alert(1)…...
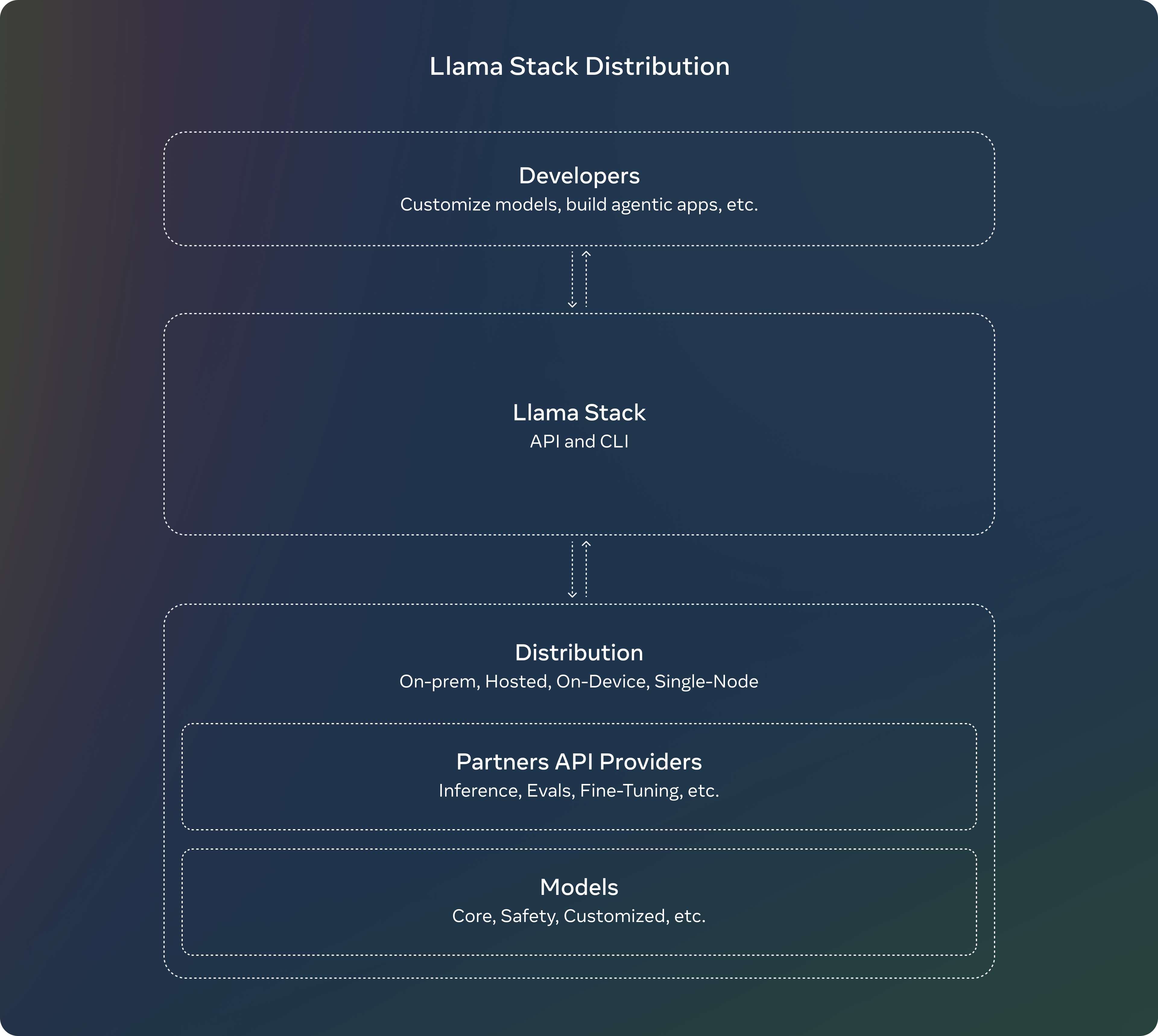
媲美GPT-4o mini的小模型,Meta Llama 3.2模型全面解读!
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,专注于分享AI全维度知识,包括但不限于AI科普,AI工…...

【leetcode】 45.跳跃游戏 ||
如果我们「贪心」地进行正向查找,每次找到可到达的最远位置,就可以在线性时间内得到最少的跳跃次数。 例如,对于数组 [2,3,1,2,4,2,3],初始位置是下标 0,从下标 0 出发,最远可到达下标 2。下标 0 可到达的…...
、yolo(txt)、voc(xml)标注格式的相互转换)
coco(json)、yolo(txt)、voc(xml)标注格式的相互转换
一般都是用labeleme进行标注 标注格式都是json 然后根据不同的格式进行数据标注转换: 1.逐个json转xml: 当我们在使用数据集训练计算机视觉模型时,常常会遇到有的数据集只给了单个的json annotation文件,而模型所需要的annotation是基于每…...
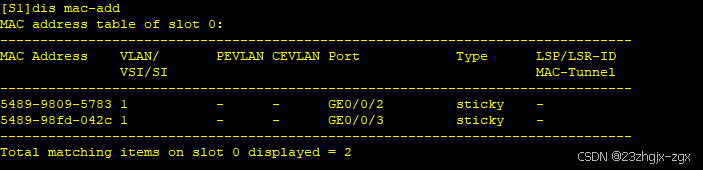
以太网交换安全:端口安全
一、端口安全介绍 端口安全是一种网络设备防护措施,通过将接口学习到的动态MAC地址转换为安全MAC地址(包括安全动态MAC和Sticky MAC),阻止除安全MAC和静态MAC之外的主机通过本接口和设备通信,从而增强设备的安全性。以…...
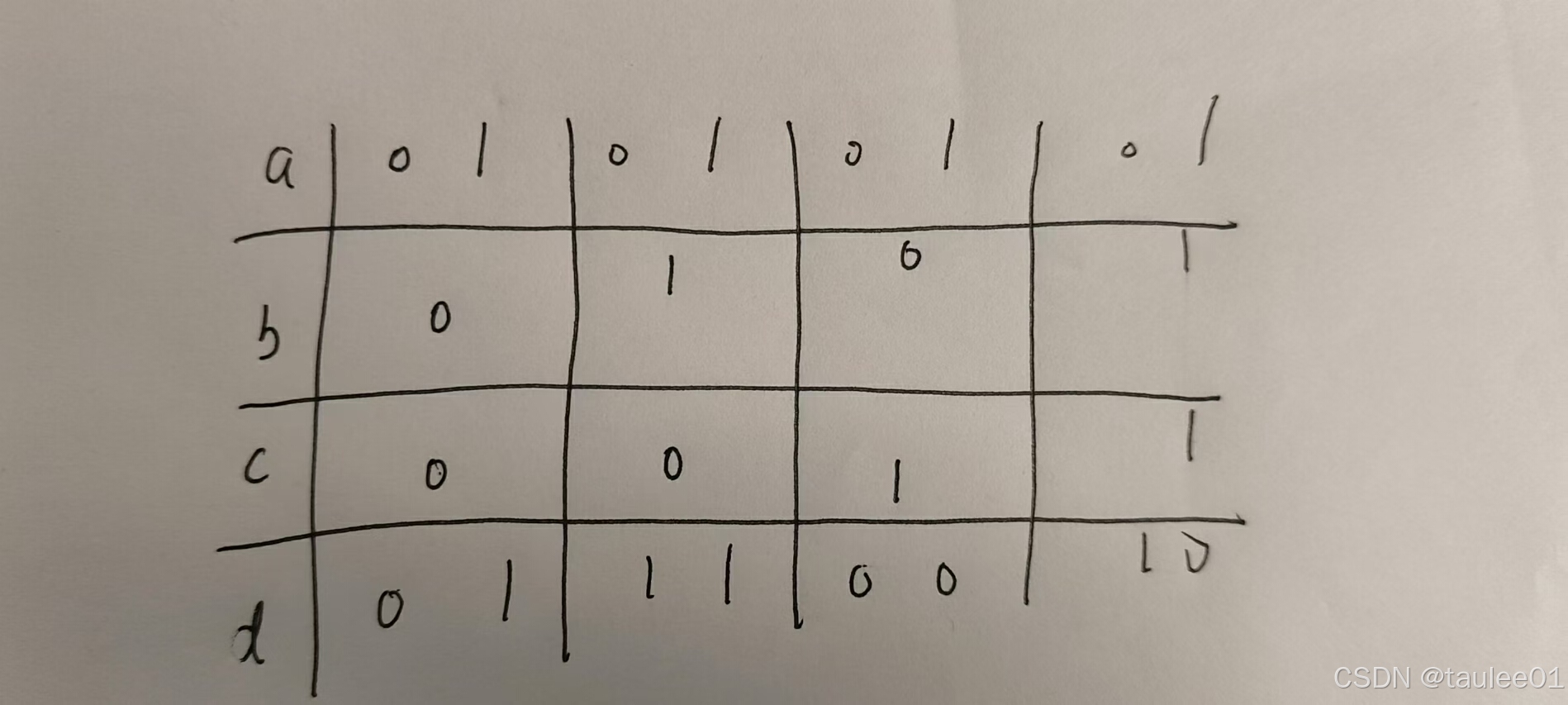
[题解] Codeforces Round 976 (Div. 2) A ~ E
A. Find Minimum Operations 签到. void solve() {int n, k;cin >> n >> k;if (k 1) {cout << n << endl;return;}int ans 0;while (n) {ans n % k;n / k;}cout << ans << endl; }B. Brightness Begins 打表发现, 翻转完后的序列为: 0…...
【零基础入门产品经理】学习准备篇 | 需要学一些什么呢?
前言: 零实习转行产品经理经验分享01-学习准备篇_哔哩哔哩_bilibili 该篇内容主要是对bilibili这个视频的观后笔记~谢谢美丽滴up主友情分享。 全文摘要:如何在0实习且没有任何产品相关经验下,如何上岸产品经理~ 目录 一、想清楚为什么…...

第四届机器人、自动化与智能控制国际会议(ICRAIC 2024)征稿
第四届机器人、自动化与智能控制国际会议(ICRAIC 2024)由湖南第一师范学院主办,南京师范大学、山东女子学院、爱迩思出版社(ELSP)协办。 大会将专注于机器人、数字化、自动化、人工智能等技术的开发和融合,…...
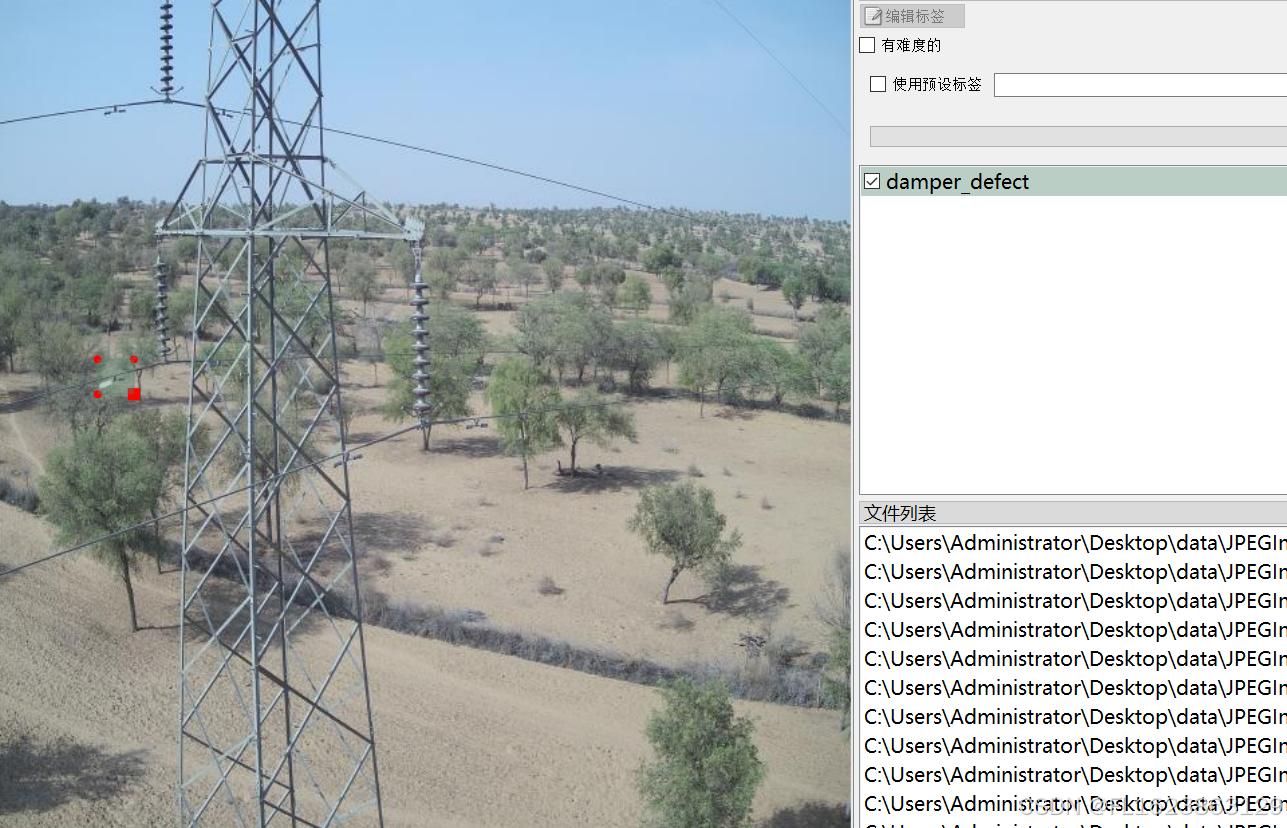
[数据集][目标检测]电力场景防震锤缺陷检测数据集VOC+YOLO格式705张1类别
重要说明:防震锤缺陷图片太难找,数据集里面存在大量单一场景图片,请仔细查看图片预览谨慎下载,此外数据集均为小目标检测,如果训练map偏低属于正常现象 数据集格式:Pascal VOC格式YOLO格式(不包含分割路径…...

【SpringBoot】
目录 一、Spring Boot概要 1. SpringBoot介绍 2. SpringBoot优点 3. SpringBoot缺点 4. 时代背景-微服务 二、Spring Boot 核心配置 1. Spring Boot配置文件分类 1.1 application.properties 1.2 application.yml 1.3 小结 2. YAML概述 3. YAML基础语法 3.1 注意事…...
Linux操作系统中MongoDB
1、什么是MongoDB 1、非关系型数据库 NoSQL,泛指非关系型的数据库。随着互联网web2.0网站的兴起,传统的关系数据库在处理web2.0网站,特别是超大规模和高并发的SNS类型的web2.0纯动态网站已经显得力不从心,出现了很多难以克服的问…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
