机器学习(1):机器学习的概念
1. 机器学习的定义和相关概念
机器学习之父 Arthur Samuel 对机器学习的定义是:在没有明确设置的情况下,使计算机具有学习能力的研究领域。
国际机器学习大会的创始人之一 Tom Mitchell 对机器学习的定义是:计算机程序从经验 E 中学习,解决某一任务 T,进行某一性能度量 P,通过 P 测定在 T 上的表现因经验 E 而提高。
机器学习是一种从数据生成规则、发现模型,来帮助我们预测、判断、分组和解决问题的技术
利用计算机的运算能力,从大量的数据中发现一个“函数”或“模型”,并通过它来模拟现实世界事物间的关系,从而实现预测、判断等目的
我们做机器学习项目,就是要选定一个算法,然后用数据训练机器,找到一族函数中最适合的那一个,形成模型。
虽然说我们希望机器最终能主动地去预测,但在此之前,机器具体选什么模型、如何训练、怎么调参,我们人类还是要在这个过程中给机器很多指导的
2. 机器学习和传统程序的区别?
- 机器学习:从已知数据中,通过不断试错、自我优化、自身总结,归纳出规则来。
- 传统程序:把已知的规则定义好后输入给机器。
3. 场景示例:
你周日约了小李、老王打牌,小李先来了,老王没来。你想打电话叫老王过来。小李说:“你别打电话啦,昨天老王喜欢的球队皇马输球了,他的项目在上个礼拜也没成功上线,再加上他儿子期末考试不及格,他肯定没心情来。
1. ”这种情况下,你觉得老王会来吗?
2. 一般情况下,我们都会觉得老王大概率不会来了。不过,你有想过我们是怎么得出这个结论的吗?
要预测老王的状况,我们就需要建立一个“预测老王会不会来”的函数,而“皇马输赢”、“项目情况”、“儿子成绩”都是输入到这个函数的自变量,我们设为 x1, x2, x3。这些自变量每一个发生变化,都会影响到函数的结果,也就是因变量 y。
相关文章:
:机器学习的概念)
机器学习(1):机器学习的概念
1. 机器学习的定义和相关概念 机器学习之父 Arthur Samuel 对机器学习的定义是:在没有明确设置的情况下,使计算机具有学习能力的研究领域。 国际机器学习大会的创始人之一 Tom Mitchell 对机器学习的定义是:计算机程序从经验 E 中学习&#…...
0. Pixel3 在Ubuntu22下Android12源码拉取 + 编译
0. Pixel3 在Ubuntu22下Android12源码拉取 编译 原文地址: http://www.androidcrack.com/index.php/archives/3/ 1. 前言 这是一个非常悲伤的故事, 因为一个意外, 不小心把之前镜像的源码搞坏了. 也没做版本管理,恢复不了了. 那么只能说是重新做一次. 再者以前的镜像太老旧…...

ip经过多个服务器转发会网速变慢吗
会的,IP经过多个服务器转发时,网速通常会变慢,主要原因包括: 增加的延迟: 每经过一个服务器,数据包就需要额外的时间进行处理和转发。这种处理时间和网络延迟会累积,导致整体延迟增加。 带宽限制…...

mongodb通过mongoimport导入JSON文件数据
目录 一、概念 二、mongoimport导入工具 三、导入命令 一、概念 MongoDB是一个流行的开源文档数据库,它支持JSON格式的文档,非常适合存储和处理大量的非结构化数据。在实际应用中,我们经常需要将大量的数据批量导入到MongoDB中。mongoimpo…...
【Qt】控件概述 (1)
控件概述 1. QWidget核心属性1.1核心属性概述1.2 enable1.3 geometry——窗口坐标1.4 window frame的影响1.4 windowTitle——窗口标题1.5 windowIcon——窗口图标1.6 windowOpacity——透明度设置1.7 cursor——光标设置1.8 font——字体设置1.9 toolTip——鼠标悬停提示设置1…...

ping基本使用详解
在网络中ping是一个十分强大的TCP/IP工具。它的作用主要为: 用来检测网络的连通情况和分析网络速度根据域名得到服务器 IP根据 ping 返回的 TTL 值来判断对方所使用的操作系统及数据包经过路由器数量。我们通常会用它来直接 ping ip 地址,来测试网络的连…...

Win10之解决:设置静态IP后,为什么自动获取动态IP问题(七十八)
简介: CSDN博客专家、《Android系统多媒体进阶实战》一书作者 新书发布:《Android系统多媒体进阶实战》🚀 优质专栏: Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏: 多媒体系统工程师系列【…...

【AI论文精读1】针对知识密集型NLP任务的检索增强生成(RAG原始论文)
目录 一、简介一句话简介作者、引用数、时间论文地址开源代码地址 二、摘要三、引言四、整体架构(用一个例子来阐明)场景例子:核心点: 五、方法 (架构各部分详解)5.1 模型1. RAG-Sequence Model2. RAG-Toke…...

踩坑spring cloud gateway /actuator/gateway/refresh不生效
版本 java version: 17 spring boot: 3.2.x spring cloud: 2023.0.3 现象 参考Spring Cloud Gateway -> Actuator API -> Refreshing the Route Cache 说明,先修改routes配置再调用/actuator/gateway/refresh,接口返回200 status,但…...

【STM32开发环境搭建】-3-STM32CubeMX Project Manager配置-自动生成一个Keil(MDK-ARM) 5的工程
目录 1 KEIL(MDK-ARM) 5 Project工程设置 2 MCU和嵌入式软件包的选择 3 Code Generator 3.1 STM32Cube Firmware Library Package 3.2 Generated files 3.3 HAL Settings 3.4 Template Settings 4 Advanced Settings 5 自动生成的KEIL(MDK-ARM) 5 Project工程目录 结…...

计算机毕业设计 Java酷听音乐系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

Java的学习(语法相关)
字符串存储的问题 char 和字符串都是字符的集合,它们之间的确有相似性,但在 Java 中它们有着不同的存储机制和处理方式。让我从 char 和 String 的本质区别入手来解释。 1. char 和 String 的区别 char 是基本类型:char 是 Java 中的基本数据…...

简单的springboot 编写Socket服务接口
简单的springboot 编写Socket服务接口 1.需求 我们项目中有部分老接口为票据接口,其中实现为java socket形式进行实现,但是其中大部分信息都是原始公司封装的包进行实现的,想要修改非常费劲,所以此处简单了解了一下socket&#…...

【Android 源码分析】Activity短暂的一生 -- 目录篇 (持续更新)
1. 前言 忽然有一天,我想要做一件事:去代码中去验证那些曾经被“灌输”的理论。 …...

VS Code使用Git Bash终端
Git Bash可以运行linux命令,在VS Code的终端界面,找到号旁边的箭头,就能直接切换了 当然,前提是安装了Git Bash,并且在资源管理器里,能鼠标右键出"Git Bash Here"...

移情别恋c++ ദ്ദി˶ー̀֊ー́ ) ——13.mapset(模拟实现)
1.对红黑树进行改造 1.1treenode模板参数改变 之前构建treenode模板参数传的是class k,class v(set为k,k;map是k,v),现在直接用T代替 template<class T> //这里直接传了T作为模板参数,T可能是pai…...

【C++】多态(下)
个人主页~ 多态(上)~ 多态 四、多态的原理1、虚表的存储位置2、多态的原理3、动态绑定和静态绑定 五、单继承和多继承关系的虚函数表1、单继承中的虚函数表2、多继承中的虚函数表 六、多态中的一些小tips 四、多态的原理 1、虚表的存储位置 class A {…...
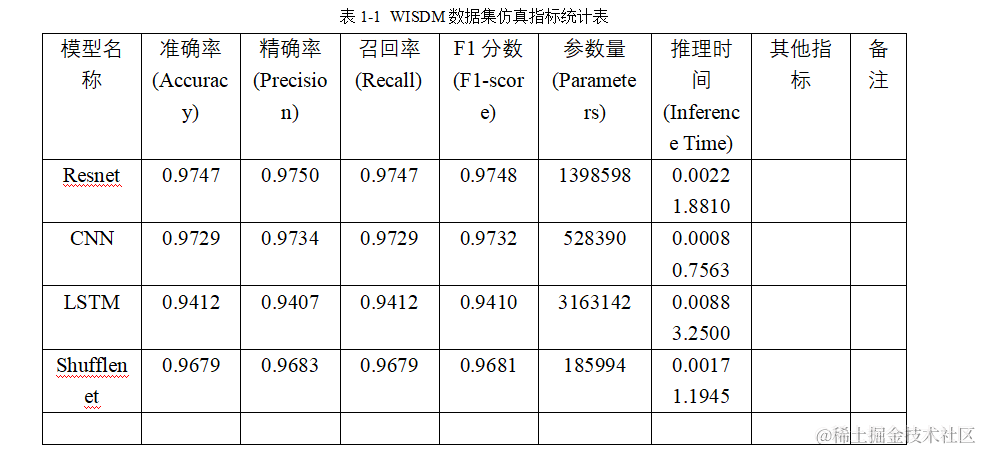
基于四种网络结构的WISDM数据集仿真及对比:Resnet、LSTM、Shufflenet及CNN
在上节中,我们已经详细介绍了WISDM数据集及如何使用CNN网络训练,得到了六个维度的模型仿真指标及五个维度的可视化分析,那么现在我们将训练模型推广到其他网路结构中去,通过仿真实验来对比一下不同网络之间对于WISDM数据集的训练效…...

【蚂蚁HR-注册/登录安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

【分布式微服务云原生】详解Redis的主从模式,主服务器挂了如何从多个从服务器选出新的主服务器
深入探索Redis主从模式:架构、故障转移与最佳实践 摘要: 本文深入探讨了Redis的主从复制模式,包括其工作原理、故障转移机制以及如何配置和管理这一模式。文章通过清晰的结构和实例代码,帮助读者理解如何在实际项目中应用Redis主…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
