决策树中联合概率分布公式解释说明
学习决策树时书本中有一公式 7-3 是:
P ( X = x i , Y = y j ) = p i j ( i = 1 , 2 , … , m , j = 1 , 2 , … , n ) P(X = x_i, Y = y_j) = p_{ij} \quad (i = 1, 2, \dots, m, \ j = 1, 2, \dots, n) P(X=xi,Y=yj)=pij(i=1,2,…,m, j=1,2,…,n)
这个公式表示的是随机变量 X X X 和 Y Y Y 的联合概率分布,其中 X X X 是一个随机变量,取值 x i x_i xi,而 Y Y Y 是另一个随机变量,取值 y j y_j yj。这些随机变量可以表示数据集的特征和对应的类别,联合概率描述了特定特征值和类别同时发生的概率。
公式的各部分解释:
-
P ( X = x i , Y = y j ) P(X = x_i, Y = y_j) P(X=xi,Y=yj):这是联合概率,表示随机变量 X X X 取值为 x i x_i xi,且随机变量 Y Y Y 取值为 y j y_j yj 的概率。这个联合概率表示了在同一时间下 X X X 和 Y Y Y 同时取到某个值的可能性。联合概率分布反映了这两个变量之间的相依关系。
-
p i j p_{ij} pij:这是联合概率的符号表示,代表了 X = x i X = x_i X=xi 且 Y = y j Y = y_j Y=yj 同时发生的概率。 p i j p_{ij} pij 是第 i i i 个 X X X 值和第 j j j 个 Y Y Y 值的联合概率。
-
i = 1 , 2 , … , m i = 1, 2, \dots, m i=1,2,…,m:这是随机变量 X X X 取的值的索引 i i i,表示 X X X 可以取 m m m 个不同的值。
-
j = 1 , 2 , … , n j = 1, 2, \dots, n j=1,2,…,n:这是随机变量 Y Y Y 取的值的索引 j j j,表示 Y Y Y 可以取 n n n 个不同的值。
联合概率的直观理解:
联合概率 P ( X = x i , Y = y j ) P(X = x_i, Y = y_j) P(X=xi,Y=yj) 衡量的是两个事件同时发生的概率。在机器学习的背景下, X X X 和 Y Y Y 可以分别表示输入特征和输出类别。例如, X X X 可能是表示特征的变量,而 Y Y Y 表示类别标签。联合概率反映了在特定输入下,输出某个类别的可能性。
举个例子,假设我们正在做一个邮件分类任务,其中 X X X 是邮件中包含的某个特定词语(如“offer”),而 Y Y Y 是该邮件的类别(垃圾邮件或正常邮件)。那么, P ( X = "offer" , Y = "垃圾邮件" ) P(X = \text{"offer"}, Y = \text{"垃圾邮件"}) P(X="offer",Y="垃圾邮件") 就表示邮件中出现“offer”这个词且该邮件为垃圾邮件的概率。
具体例子:
假设我们有一个简单的二元分类问题(比如垃圾邮件分类),数据集中的每个样本由两个特征 X 1 X_1 X1 和 X 2 X_2 X2 组成,且每个样本属于两个可能的类别之一 Y Y Y,分别是“垃圾邮件”和“正常邮件”。现在,我们定义联合概率分布:
- X 1 X_1 X1 可以取 x 1 x_1 x1 和 x 2 x_2 x2 两个值,分别表示邮件包含或不包含某个特定词汇(如“offer”)。
- X 2 X_2 X2 也可以取 x 1 x_1 x1 和 x 2 x_2 x2 两个值,表示邮件包含或不包含另一个特定词汇(如“free”)。
- Y Y Y 取 y 1 y_1 y1 表示垃圾邮件,取 y 2 y_2 y2 表示正常邮件。
联合概率分布中的各项值 P ( X = x i , Y = y j ) P(X = x_i, Y = y_j) P(X=xi,Y=yj) 代表了邮件中包含某些词语时,它属于垃圾邮件或正常邮件的概率。例如:
- P ( X = "offer" , Y = "垃圾邮件" ) = 0.3 P(X = \text{"offer"}, Y = \text{"垃圾邮件"}) = 0.3 P(X="offer",Y="垃圾邮件")=0.3:表示当邮件包含“offer”时,它被分类为垃圾邮件的概率为 30%。
- P ( X = "offer" , Y = "正常邮件" ) = 0.1 P(X = \text{"offer"}, Y = \text{"正常邮件"}) = 0.1 P(X="offer",Y="正常邮件")=0.1:表示当邮件包含“offer”时,它是正常邮件的概率为 10%。
联合概率计算的具体步骤
联合概率与条件概率的关系:
联合概率与条件概率有着密切的关系。通过联合概率,我们可以计算条件概率。条件概率表示在已知某一事件发生的情况下,另一个事件发生的概率。在我们的例子中,条件概率 P ( Y = 垃圾邮件 ∣ X = "offer" ) P(Y = \text{垃圾邮件} | X = \text{"offer"}) P(Y=垃圾邮件∣X="offer") 表示当我们已知邮件包含“offer”这个词时,它被分类为垃圾邮件的概率。条件概率可以通过联合概率计算得出:
P ( Y = y j ∣ X = x i ) = P ( X = x i , Y = y j ) P ( X = x i ) P(Y = y_j | X = x_i) = \frac{P(X = x_i, Y = y_j)}{P(X = x_i)} P(Y=yj∣X=xi)=P(X=xi)P(X=xi,Y=yj)
这个公式表示已知 X = x i X = x_i X=xi 时,发生 Y = y j Y = y_j Y=yj 的概率,可以通过 X = x i X = x_i X=xi 和 Y = y j Y = y_j Y=yj 同时发生的概率 P ( X = x i , Y = y j ) P(X = x_i, Y = y_j) P(X=xi,Y=yj) 除以 X = x i X = x_i X=xi 的边缘概率来计算。
总结:
公式 7-3 表示随机变量 X X X 和 Y Y Y 的联合概率分布。联合概率分布帮助我们了解多个变量之间的相依关系,是许多机器学习算法(包括决策树、贝叶斯分类器等)的基础。在具体任务中,联合概率可以帮助我们计算输入特征与输出标签之间的关联,并在此基础上进行分类或预测。
相关文章:

决策树中联合概率分布公式解释说明
学习决策树时书本中有一公式 7-3 是: P ( X x i , Y y j ) p i j ( i 1 , 2 , … , m , j 1 , 2 , … , n ) P(X x_i, Y y_j) p_{ij} \quad (i 1, 2, \dots, m, \ j 1, 2, \dots, n) P(Xxi,Yyj)pij(i1,2,…,m, j1,2,…,n) 这个公式表示的是随机变…...

计算机毕业设计 农场投入品运营管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

php email功能实现:详细步骤与配置技巧?
php email发送功能详细教程?如何使用php email服务? 无论是用户注册、密码重置,还是订单确认,电子邮件都是与用户沟通的重要手段。AokSend将详细介绍如何实现php email功能,并提供一些配置技巧,帮助你更好…...

MapBox Android版开发 6 关于Logo
MapBox Android版开发 6 关于Logo Logo的显示查看源码及思路(Logo)第一步第二步 隐藏Logo示例查看源码及思路(Info)第一步第二步 隐藏Logo和Info示例 看到有网友留言问如何移除Logo,今天看了下V9源码,发现M…...

2024年房市
24年8月15日,国家统计局公布,“7月末,商品房待售面积73926万平方米”。(原文链接:https://www.stats.gov.cn/sj/zxfb/202408/t20240815_1955982.html) 7.39亿平方存量商品房,估价均价1万每平,总价约&am…...

index索引
index索引: create index 【1】on 【2】(【3】) 1为索引名,通常为id_表名_列名。2为表名。3为列名。 CREATE INDEX id_account_id ON account(id); -- 根据id创建索引 CREATE INDEX id_account_idname on account(id,name); -- 创建组合索引 索…...

理解互联网链路:从本地ISP到Tier 1 ISP运营商
1. 互联网服务提供商(ISP) 互联网服务提供商(ISP)是指提供互联网接入服务的公司或组织。它们负责将用户连接到互联网,并提供相关的服务,如电子邮件、网站托管和其他在线服务。ISP可以分为不同的层级&#…...

基于元神操作系统实现NTFS文件操作(三)
1. 背景 本文主要介绍DBR的读取和解析,并提供了基于元神操作系统的实现代码。由于解析DBR的目的是定位到NTFS磁盘分区的元文件$Root进行文件操作,所以只解析了少量的部分,其它部分可以参考相关文档进行理解。 DBR存在于磁盘分区的第一个扇区…...

深度学习与数学归纳法
最近发现,深度学习可以分为两个主要的阶段,分别是前向推理以及反向传播,分别对应着网络的推理和参数训练两个步骤。其中推理有时候也称为归纳推理。 在做参数训练的时候,本质上是在利用历史数据求网络参数的先验分布; …...

《Linux从小白到高手》理论篇(六):Linux软件安装一篇通
List item 本篇介绍Linux软件安装相关的操作命令,看完本文,有关Linux软件安装相关操作的常用命令你就掌握了99%了。 Linux软件安装 RPM RPM软件的安装、删除、更新只有root权限才能使用;查询功能任何用户都可以操作;如果普通用…...
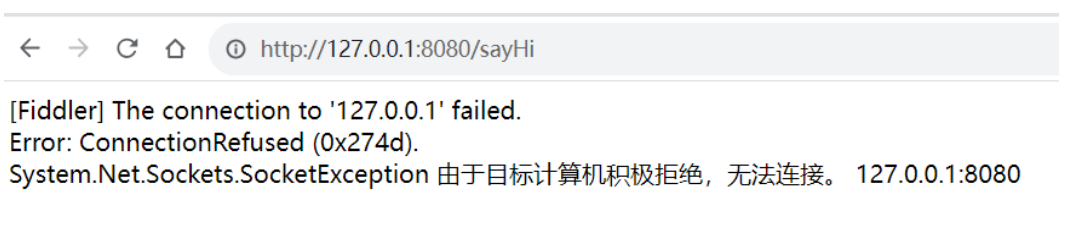
【Spring】运行Spring Boot项目,请求响应流程分析以及404和500报错
1. 运行项目 import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; SpringBootApplication public class Application { public static void main(String[] args) { SpringApplication.run(Appl…...
②EtherCAT转Modbus485RTU网关多路同步高速采集无需编程串口服务器
EtherCAT转Modbus485RTU网关多路同步高速采集无需编程串口服务器https://item.taobao.com/item.htm?ftt&id798036415719 EtherCAT 串口网关 EtherCAT 转 RS485 (接上一章) 自由协议通信步骤 (以MS-A2-1041为例) 接收与…...

matlab-对比两张图片的HSV分量的差值并形成直方图
%对比两张图片的HSV分量的差值并形成直方图,改个路径就能用,图片分辨率要一致 close all; clear all; clc; I1imread(E:\test\resources\image\1.jpg); I2imread(E:\test\resources\image\2.jpg); HSV1 rgb2ntsc(I1); HSV2 rgb2ntsc(I2); %HSV,HSV 代…...

微服务SpringGateway解析部署使用全流程
官网地址: Spring Cloud Gateway 目录 1、SpringGateway简介 1、什么是网关 2、为什么用网关【为了转发】 2、应用: 1.启动nacos 2.创建网关项目 3.网关配置1 4.网关配置2【了解】 5.过滤器配置【了解】 1、SpringGateway简介 核心功能有三个&…...

Solidity 存储和内存管理:深入理解与高效优化
在 Solidity 中,存储和内存管理是编写高效智能合约的关键组成部分。合约执行的每一步操作都可能涉及到数据的存储和读取,而这些操作对 gas 的消耗有很大影响。因此,理解 Solidity 的存储模型以及如何优化数据的管理对于合约的安全性、性能和成…...

机器学习篇-day02-KNN算法实现鸢尾花模型和手写数字识别模型
一. KNN简介 KNN思想 K-近邻算法(K Nearest Neighbor,简称KNN)。比如:根据你的“邻居”来推断出你的类别 KNN算法思想:如果一个样本在特征空间中的k 个最相似的样本中的大多数属于某一个类别,则该样本也属…...

【C++】STL--vector
1.vector的介绍 我们先来看看vector的文档介绍,实际中我们只要熟悉相关接口就好了。 成员函数 使用STL的三个境界:能用,明理,能扩展 ,那么下面学习vector,我们也是按照这个方法去学习 2 vector的使用 v…...

Java使用Redis的详细教程
Redis是一个基于内存的key-value结构数据库,即非关系型数据库,具有高性能、丰富的数据类型、持久化、高可用性和分布式等特点。在Java项目中,Redis通常用于缓存、分布式锁、计数器、消息队列和排行榜等场景。以下是在Java中使用Redis的详细教…...

严重 Zimbra RCE 漏洞遭大规模利用(CVE-2024-45519)
攻击者正在积极利用 CVE-2024-45519,这是一个严重的 Zimbra 漏洞,该漏洞允许他们在易受攻击的安装上执行任意命令。 Proofpoint 的威胁研究人员表示,攻击始于 9 月 28 日,几周前,Zimbra 开发人员发布了针对 CVE-2024-…...

php函数积累
对称函数 isset 判断数组arr中是否存在键key 返回值true/false isset(name,$arr) unset 删除数组中的键 需存在key不然抛出异常 unset($arr[name]) json_encode 数据转json格式 json_encode($arr) 一般形式 指定字符编码形式 json_decode json格式转原有数据格式 json_d…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
