【数据结构】二叉树<遍历>
【二叉树遍历】|-前序-中序-后序-层序-|
- <二叉树的遍历>
- 1.前序遍历【递归】
- 2.中序遍历【递归】
- 3.后序遍历【递归】
- 4.层序遍历【非递归】
- 4.1判断是否是完全二叉树
<二叉树的遍历>
在学习二叉树遍历之前我们先了解下二叉树的概念。
二叉树是:
1.空树
2.非空:根节点,根节点的左子树,根节点的右子树构造。
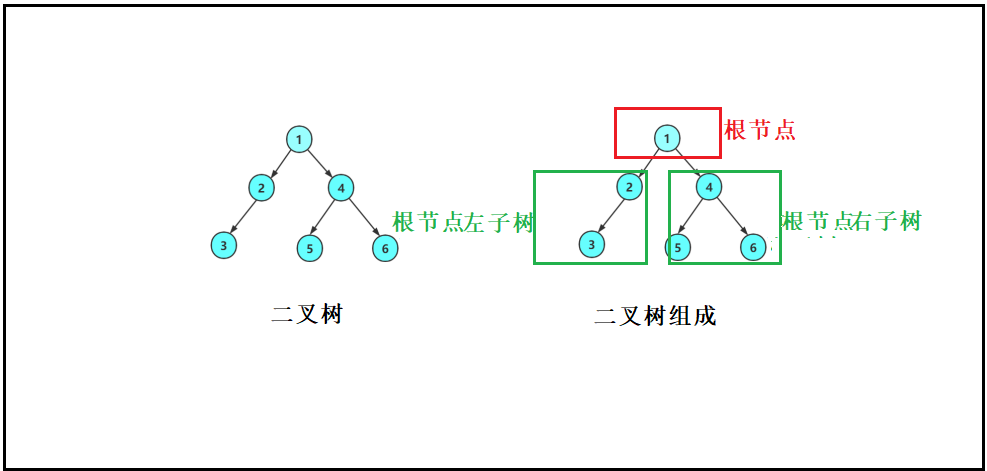
学习二叉树结构,最简单的方式就是遍历了。
二叉树的遍历就是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个节点只操作一次。
访问结点所做的操作依赖于具体的应用问题。
二叉树的遍历分为
1.<前序遍历>[Preorder Traversal]
访问根节点的操作发生在遍历左右子树之前。
也就是对于一个节点,它要求先访问这个节点的内容,然后再去遍历左子树,当左子树遍历完后,再遍历右子树。
2.<中序遍历>[Inorder Traversal]
访问根节点的操作发生在遍历其左右子树之中
也就是对于一个节点,它要求先遍历左子树,当左子树都遍历完,再回来访问节点里的内容,然后再遍历右子树。
3.<后续遍历>[Postorder Traversal]
访问根节点的操作发生在遍历其左右子树之后
也就是对于一个节点,它要求先遍历完左子树,再遍历完右子树,最后回来的时候再访问节点的内容。
4.<层序遍历>
层序遍历,顾名思义,一层一层的遍历即可。
从第一层开始遍历,遍历完第一层再遍历下一层。
我们为了好验证二叉树的遍历操作,手动创造一个二叉树,也就是下图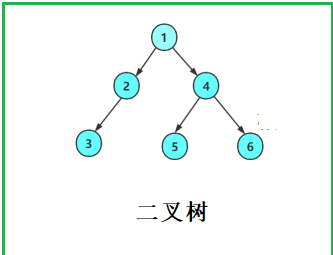
这样,用代码来实现就是这样:
#include <stdio.h>
#include <stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
BTNode* BuyNode(BTDataType x)
{BTNode* ret =(BTNode*)malloc(sizeof(BTNode));ret->data = x;ret->left = NULL;ret->right = NULL;return ret;
}
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}
1.前序遍历【递归】
我们为了真正展现前序遍历在二叉树中是如何实现的,将空节点也打印出来。这样就可以清晰的看出来遍历的过程。
// 二叉树前序遍历-<根节点-左子树-右子树>-
void PreOrder(BTNode* root)
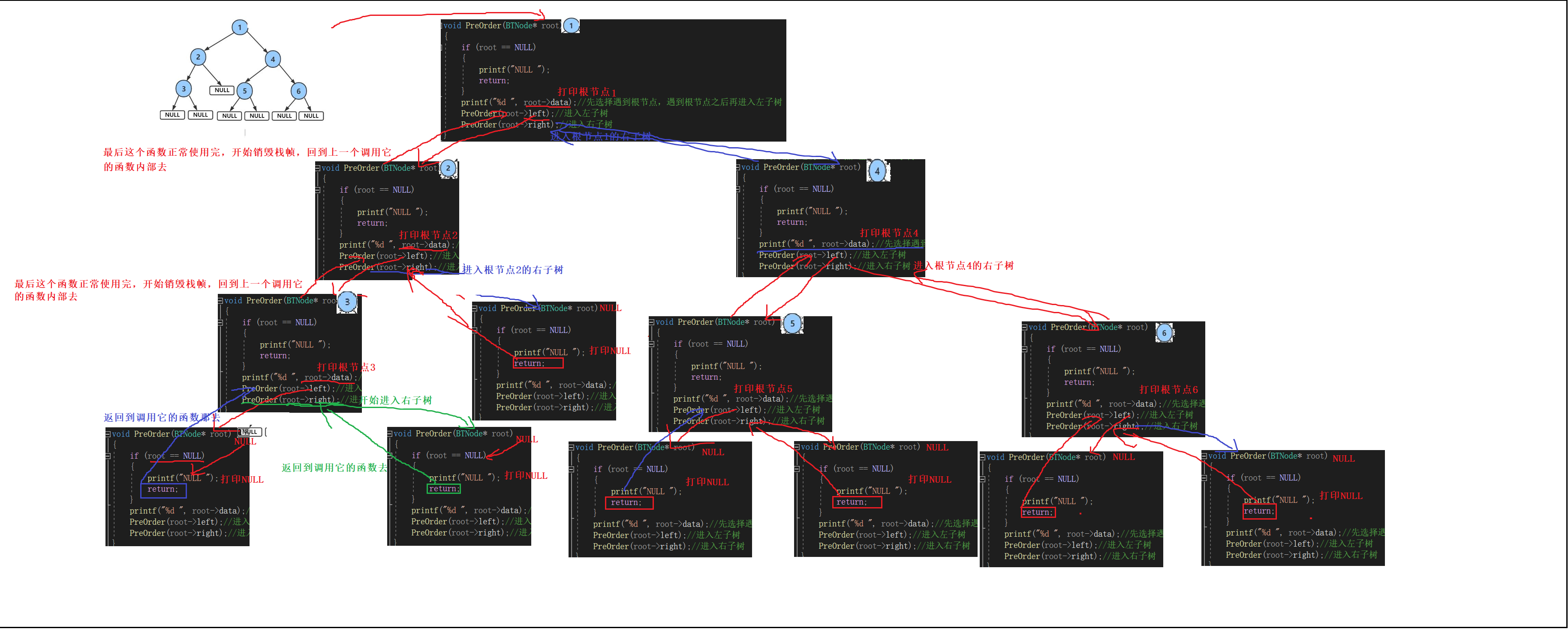
{if (root == NULL)//如果遇到空节点就返回{printf("NULL ");return;}printf("%d ", root->data);//先访问根节点内容,打印完节点内容后再进入左子树。PreOrder(root->left);//进入左子树PreOrder(root->right);//进入右子树
}
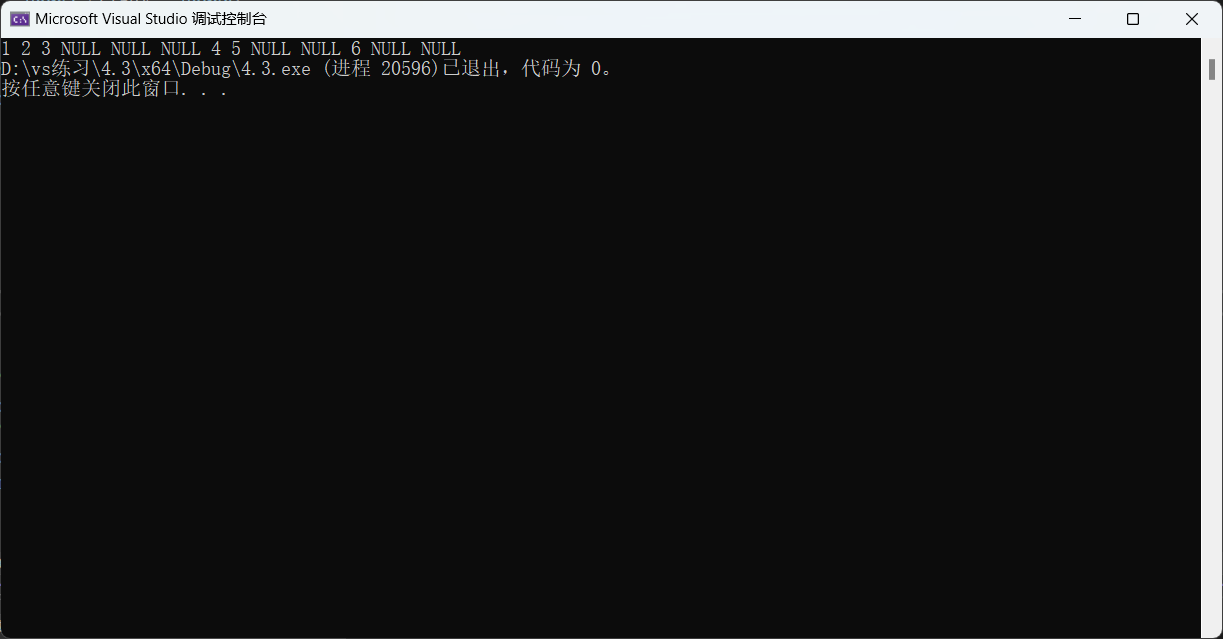
根据结果你能想明白怎么遍历的吗?
递归展开图:
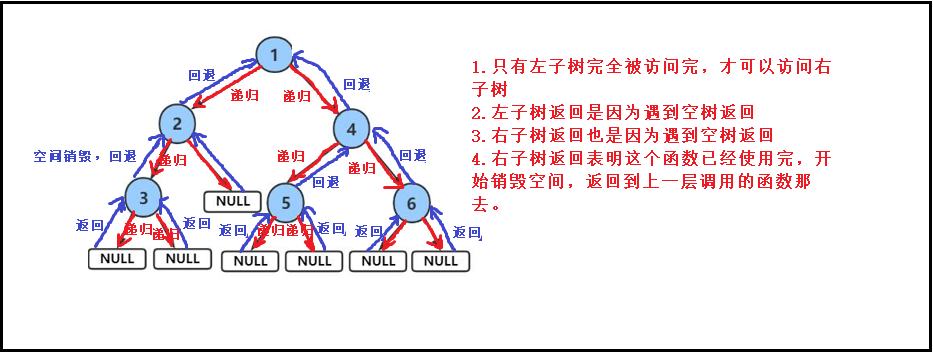
2.中序遍历【递归】
// 二叉树中序遍历
void InOrder(BTNode* root)
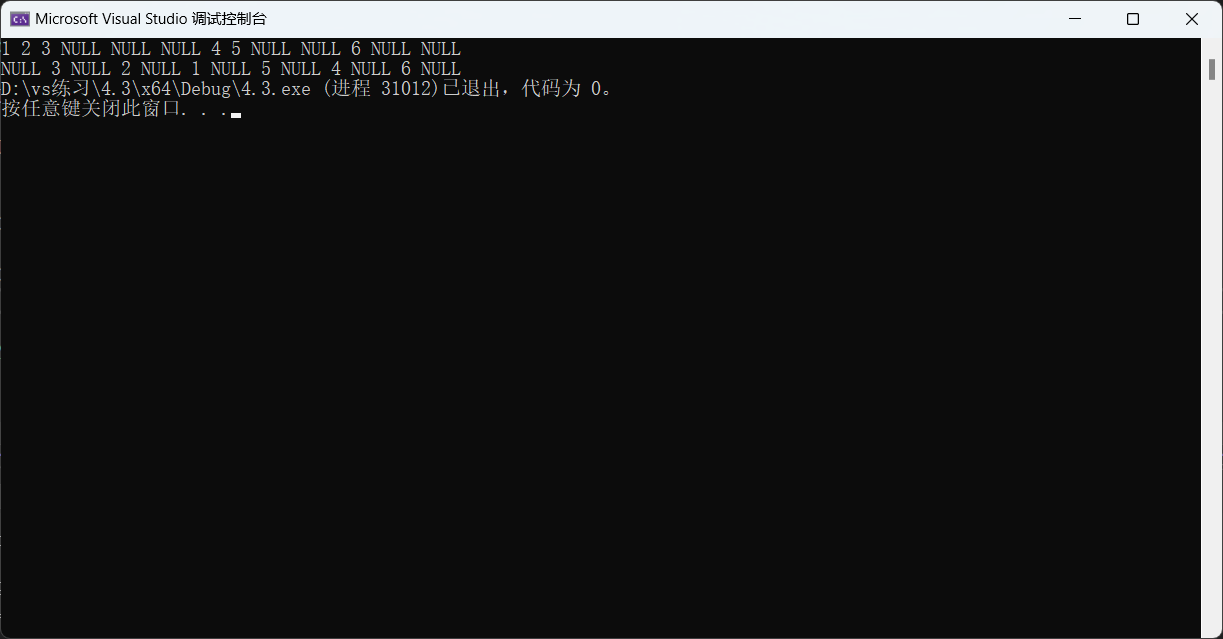
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);//先遍历左子树printf("%d ", root->data);//遍历完左子树后再访问节点内容InOrder(root->right);//访问完节点内容后再遍历右子树
}
递归展开图
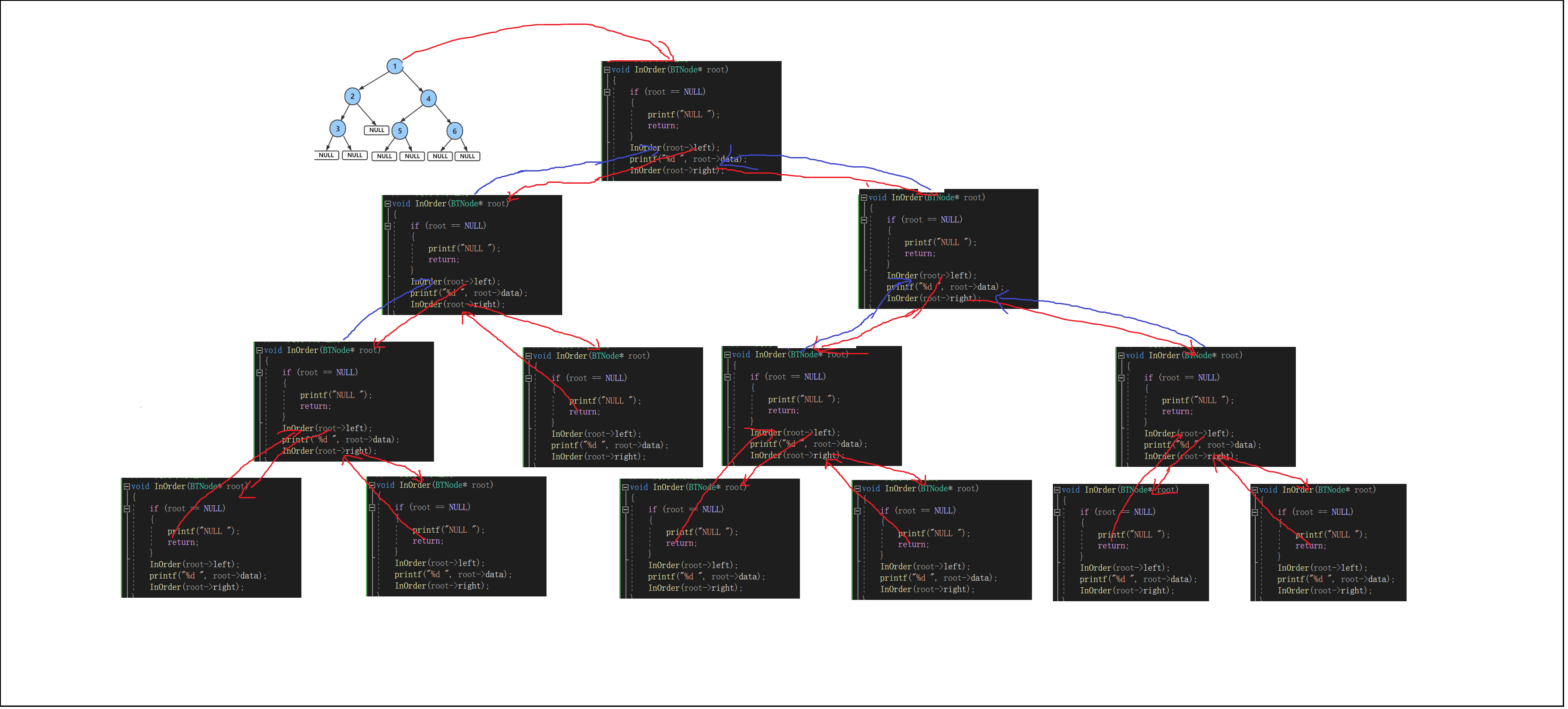
3.后序遍历【递归】
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

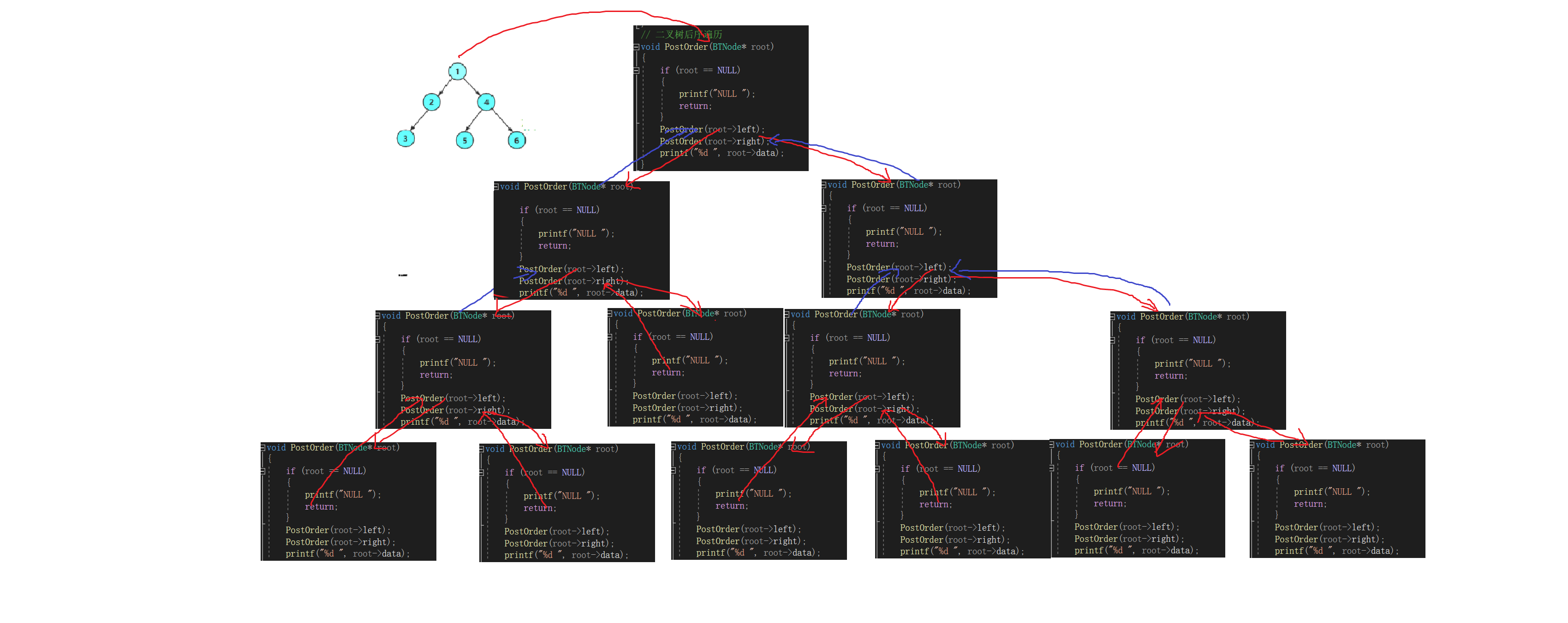
而后序遍历这种特点很适合用在二叉树的销毁上去。
因为相比较前序遍历,如果先销毁了节点,那它的左右子树就无法找到了。
但后续遍历不一样,后序遍历是先遍历左右子树,最后再访问节点。
所以我们只要使用后序遍历,先销毁左右子树,再销毁节点就可以了。
比如:二叉树的销毁
void BTreeDestroy(BTNode* root)
{if (root == NULL){return;}BTreeDestroy(root->left);//先销毁左子树BTreeDestroy(root->right);//再销毁右子树free(root);//最后再销毁节点root = NULL;
}
4.层序遍历【非递归】
上面三个都是属于递归形式的遍历,层序遍历是非递归的。
怎么进行层序遍历呢?
这个就需要用到队列来解决了。
思想:
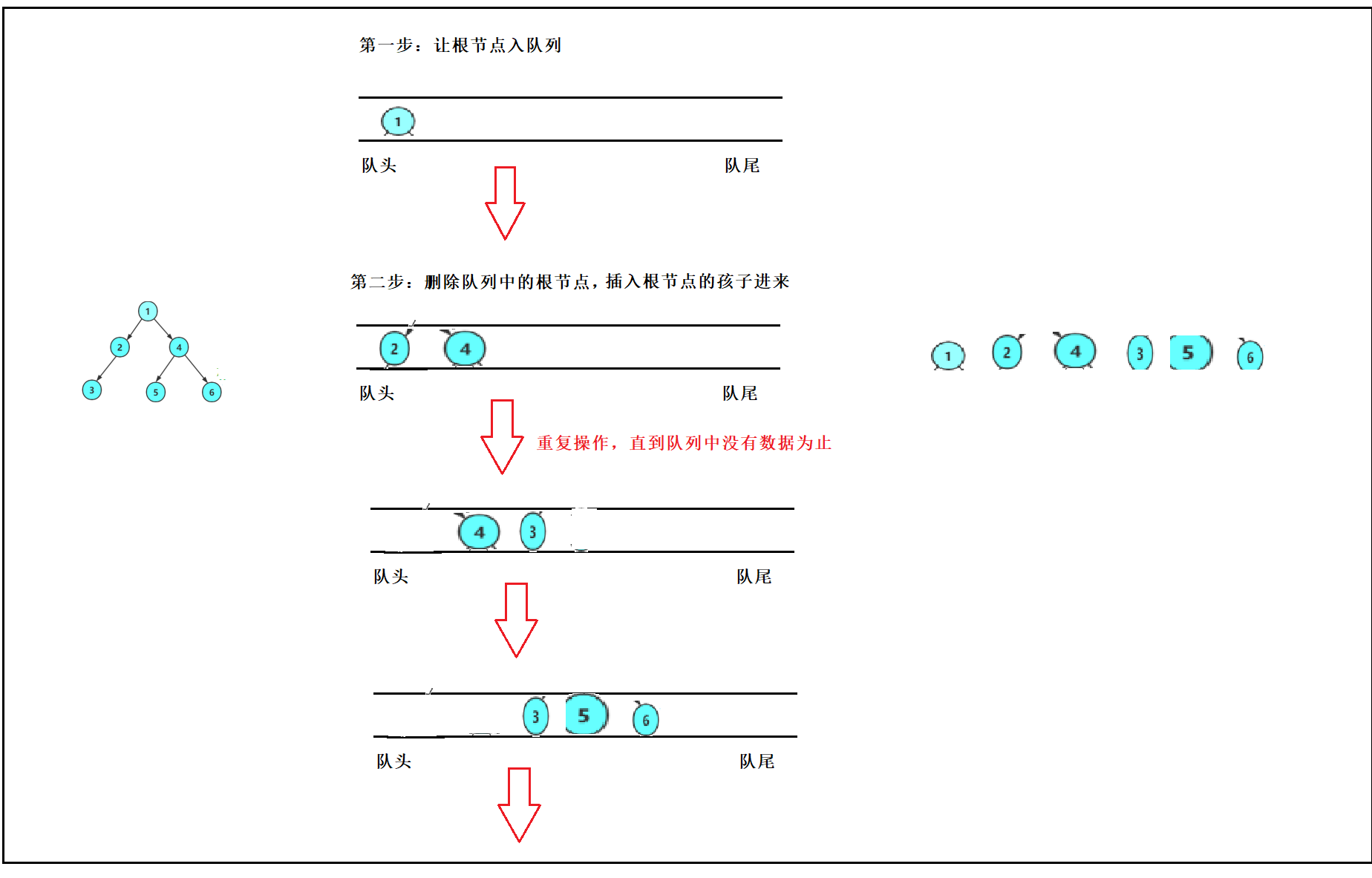
出上一层,带入下一层。
一开始让根节点入队列,那队列中就有元素存在,不是空队列了。
然后接下来就是不断的出队列中的根节点,每一次出队列中的根节点时,都要将
该根节点的孩子插入到队列的后面去。 也就是出根节点,带入它们的孩子进来。直到队列中没有数据为止。
不过注意的是,队列中不是真正节点,而是指向节点的指针,如果将节点插入进去,那怎么找到它们的孩子呢?
所以我们插入进入的是指向节点的指针。
typedef struct BTreeNode* QData;//注意这里将队列中元素的类型改成指向节点的指针
typedef struct QNode
{struct QNode* next;QData data;//队列的元素是指向节点的指针
}QNode;
//因为队列的数据结构操作需要找尾,这就需要传多个参数了,很麻烦,所以我们再分装个结构体将多个数据变成一个
typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;
void QueueInit(Queue *pq);//初始化队列
void QueueDestroy(Queue *pq);//销毁队列
void QueuePush(Queue*pq ,QData x);//入队,从队尾插入一个数据,尾删
void QueuePop(Queue *pq);//出队,从队头删除数据,头删
bool QueueEmpty(Queue *pq);//判断队列是否为空
int QueueSize(Queue*pq);//获得队列有效数据个数大小
QData QueueFront(Queue*pq);//获取队头数据
QData QueueBack(Queue*pq);//获取队尾数据
#include "queue.h"
void QueueInit(Queue* pq)//初始化队列
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}
void QueueDestroy(Queue* pq)//销毁队列
{QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;pq->size = 0;
}
void QueuePush(Queue* pq, QData x)//入队,从队尾插入一个数据,尾删
{assert(pq);
/* QNode* cur = pq->head;*/QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc");}newnode->data=x;newnode->next = NULL;if (pq->head == NULL){//赋值pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;//更新tail的位置pq->tail = newnode;}pq->size++;}
void QueuePop(Queue* pq)//出队,从队头删除数据,头删
{assert(pq);//头删之前需要判断链队列是否为空assert(pq->head!=NULL);QNode* next = pq->head->next;free(pq->head);pq->head = next;if (pq->head==NULL)//只管头删,最后再处理。{pq->tail=NULL;}pq->size--;
}bool QueueEmpty(Queue* pq)//判断队列是否为空----主要size的作用
{assert(pq);return pq->size == 0;//return pq->head=pq->tailk=NULL;
}
int QueueSize(Queue* pq)//获得队列有效数据个数大小
{assert(pq);return pq->size;
}QData QueueFront(Queue* pq)//获取队头数据
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QData QueueBack(Queue* pq)//获取队尾数据
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}以上是创建一个队列,接下来就是进行二叉树的层序遍历了。
void LevOlder(BTNode* root)//层序遍历--
{Queue q;//定义一个队列QueueInit(&q);//初始化队列//首先将根 指针插入到队列里去if (root){QueuePush(&q, root);}//再出上一层带入下一层while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);//保存一下这个要出队列的指向结点的指针QueuePop(&q);printf("%d ", front->data);//出完后再将它的孩子指针带入进来if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
4.1判断是否是完全二叉树
如何判断一个二叉树树是否是完全二叉树呢?
首先我们需要了解什么是完全二叉树
【完全二叉树】
1.前n-1层都是满的二叉树。
2.最后一层从左到右是连续的。
特点:
1.非空节点是连续的。
2.空节点也是连续的。
3.至多有一个度为1的节点。
我们根据完全二叉树非空节点都是连续的这一特性,来作下面的思路:
如果对完全二叉树进行层序遍历,那么第一次出现空节点的地方就是最后一个节点的后面。 而后面就不能再出现非空节点了,后面应该都是空。
所以我们可以做出这样判断:层序遍历二叉树,如果第一次出现空之后,再出现非空节点的一定不是完全二叉树,如果后面只有空则是完全二叉树。
不过要注意的是,这里的层序遍历与原来的层序遍历不一样,原来的层序遍历,只会将根节点插入到队列中去,不会将空节点插入到队中去,而现在需要将空节点也插入到队列中去,如果出队列中的元素,出出队列的是一个空节点,那么我们就可以进行判断,是否后面还会出现非空节点呢?
//判断是否是完全二叉树,利用完全二叉树性质--非空结点是连续的,一旦出现空,后面就不应该再出现空结点。所以利用层序遍历,当第一次出现
//空时,就可以进行判断后面是否会出现非空结点。这里不同与普通层序遍历,NULL也进队列,而且出队列的结点有两种可能一种为空,一种不为空,不像层序遍历只出非空结点
{
bool BTreeCompele(BTNode* root)
{Queue q;QueueInit(&q);if (root)//将根节点插入到队列中{QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//出队列中的元素if (front == NULL){break;}//如果front不为空,就将它的孩子插入到队列中去,空节点也插入进去,不需要讨论QueuePush(&q, front->left);QueuePush(&q, front->right);}//break 跳出来需要判断是否后面还会出现非空节点while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//出队列中的元素if (front)//如果队列中出的节点不为空节点{QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
相关文章:

【数据结构】二叉树<遍历>
【二叉树遍历】|-前序-中序-后序-层序-|<二叉树的遍历>1.前序遍历【递归】2.中序遍历【递归】3.后序遍历【递归】4.层序遍历【非递归】4.1判断是否是完全二叉树<二叉树的遍历> 在学习二叉树遍历之前我们先了解下二叉树的概念。 二叉树是: 1.空树 2.非空…...

linux查看硬件信息
dmidecode用于在linux下获取硬件信息,遵循SMBIOS/DMI标准,可获取包括BIOS、系统、主板、处理器、内存、缓存等等硬件信息 1、查看CPU信息cat /proc/cpuinfo、lscpu 型号:cat /proc/cpuinfo|grep name|cut -f2 -d:|uniq -c 物理核:…...

吐血整理,互联网大厂最常见的 1120 道 Java 面试题(带答案)整理
前言 作为一个 Java 程序员,你平时总是陷在业务开发里,每天噼里啪啦忙敲着代码,上到系统开发,下到 Bug 修改,你感觉自己无所不能。然而偶尔的一次聚会,你听说和自己一起出道的同学早已经年薪 50 万&#x…...
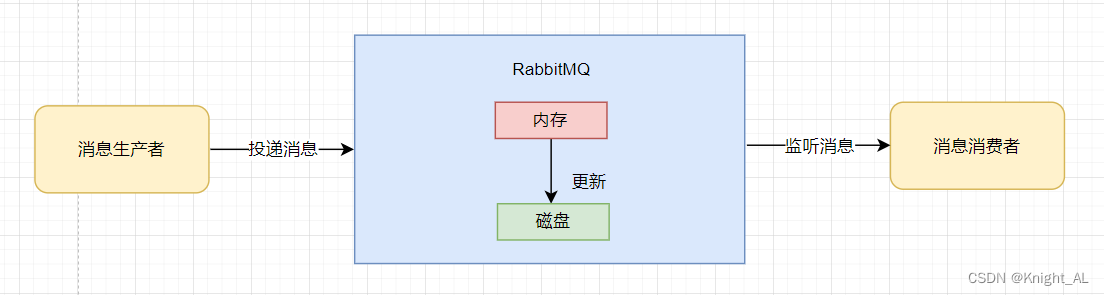
RabbitMQ如何避免消息丢失
目录1.生产者没有成功把消息发送到MQ2.RabbitMQ接收到消息之后丢失了消息3.消费者弄丢了消息前言 首先明确一点一条消息的传送流程:生产者->MQ->消费者 我们根据这三个依次讨论 1.生产者没有成功把消息发送到MQ 丢失的原因:因为网络传输的不稳定…...
)
做算法题的正确姿势(不断更新)
不停的反思自己,总结建议 做一道算法题,不能去死磕。 如果看一道题,半小时内,没有清晰的思路,就看题解!!!你可能觉得你有点思路,就往里死钻,结果可能就像进…...

p85 CTF夺旗-JAVA考点反编译XXE反序列化
数据来源 图片来源 Java 常考点及出题思路 考点技术:xxe,spel 表达式,反序列化,文件安全,最新框架插件漏洞等 设法间接给出源码或相关配置提示文件,间接性源码或直接源码体现等形式 https://www.cnblog…...

FastJson——JSO字符串与对象的相互转化
一、FastJson介绍 Fastjson是阿里巴巴的开源SON解析库它可以解析JSON格式的字符串,支持将java Bean序列化为ISON字符串,也可以从JSON字符串反序列化到JavaBean。 Fastjson的优点 速度快 fastjson相对其他JSON库的特点是快,从2011年fastj…...
《程序员面试金典(第6版)》面试题 08.08. 有重复字符串的排列组合(回溯算法,全排列问题)C++
题目描述 有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。 示例1: 输入:S “qqe” 输出:[“eqq”,“qeq”,“qqe”] 示例2: 输入:S “ab” 输出:[“ab”, “ba”] 提示: 字符都是英文字母。…...

k8s API限流——server级别整体限流和客户端限流
1. 背景 为了防止突发流量影响apiserver可用性,k8s支持多种限流配置,包括: MaxInFlightLimit,server级别整体限流Client限流EventRateLimit, 限制eventAPF,更细力度的限制配置 1.1 MaxInFlightLimit限流 apiserver…...

在华为做了三年软件测试被裁了,我该怎么办
近年来,随着经济环境的变化和企业战略的调整,员工被裁员的情况变得越来越普遍。无论是因为企业经营困难还是因为业务调整,员工们都可能面临被裁员的风险。如果你也遇到了这样的情况,那么你应该怎么办呢? 首先…...

Spring cloud 限流的多种方式
在频繁的网络请求时,服务有时候也会受到很大的压力,尤其是那种网络攻击,非法的。这样的情形有时候需要作一些限制。本文主要介绍了两种限流方法,感兴趣的可以了解一下 目录 一、实战基于 Spring cloud Gateway 的限流 二、基于阿…...
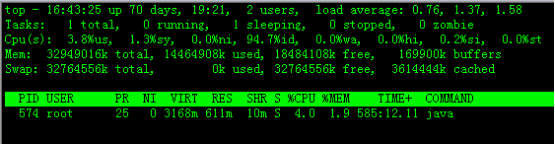
Linux命令·top
top命令是Linux下常用的性能分析工具,能够实时显示系统中各个进程的资源占用状况,类似于Windows的任务管理器。下面详细介绍它的使用方法。top是一个动态显示过程,即可以通过用户按键来不断刷新当前状态.如果在前台执行该命令,它将独占前台,直到用户终止…...

springmvc之系列文章
springmvc之编程步骤 springmvc初始化过程 用WebServlet和WebFilter干掉web.xml 没有web.xml怎么写web程序 一次GET请求在springmvc中是的处理流程 springMVC的handler都有哪些类型 springmvc主要组件简单介绍 springmvc 的Servlet WebApplicationContext springmvc 的…...
)
Matlab实现深度学习(附上完整仿真源码)
文章目录简单案例完整仿真代码下载简单案例 深度学习是一种能够自动学习和提取数据特征的机器学习方法,它已经在图像识别、语音识别、自然语言处理等领域取得了显著的成果。而Matlab作为一个强大的数学计算工具,也提供了丰富的深度学习工具箱࿰…...
我的谷歌书签
Form 表单 | Element Plusa Vue 3 based component library for designers and developershttps://element-plus.gitee.io/zh-CN/component/form.html#%E5%AF%B9%E9%BD%90%E6%96%B9%E5%BC%8F three.js exampleshttp://www.yanhuangxueyuan.com/threejs/examples/#software_geo…...
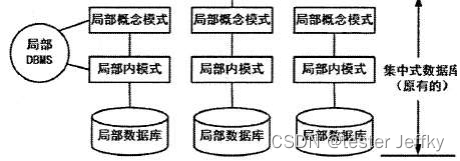
day3 数据库技术考点汇总
一、重点知识点 基本概念:三级模式-两级映像、数据库设计数据库模型:E-R模型、关系模型、关系代数(结合SQL语言)规范化:函数依赖、健与约束、范式、模式分解事务并发:并发三种问题、三级封锁协议数据库新技…...
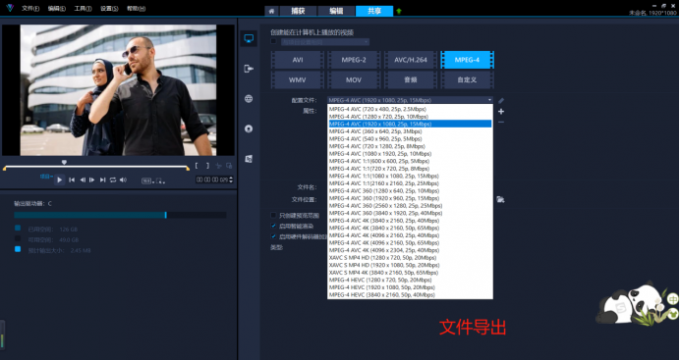
学剪辑难吗 如何使用会声会影2023做剪辑视频
很多剪辑初学者都问过一个问题,学剪辑难吗?其实不论学什么,只要用心学都不难,今天我们就来讲讲如何学做剪辑视频,感兴趣的小伙伴们不要走开!一、学剪辑难吗 其实学剪辑并不是件难事,但是需要掌握…...

django学习日记
1、虚拟环境 virtualenv "加虚拟环境名字" 在当前目录下创建一个虚拟环境 进入虚拟环境执行activate进入该虚拟环境,再执行deactivate退出虚拟环境 安装一个包来管理虚拟环境,每次创建虚拟环境都放到同一位置,以及在任意位置都可…...

在线教学视频课程如何防止学员挂机?
阿酷TONY / 2023-3-31 / 长沙 / 原创 / 要不?交个朋友吧? 在线教学视频课程如何防止学员挂机?siri:这是个有意思的问题哈~~~在线教育、在线企业培训机构通常是如何处理的呢? 答:在视频播放过程中,弹出问题…...

【Redis】安装配置
文章目录Redis简介Redis版本迭代Redis安装配置官网地址操作系统环境基础查看本地redis版本修改配置文件docker容器安装redis测试linux版Redis简介 简介 与传统数据库关系(mysql),Redis是key-value数据库(NoSQL一种),mysql是关系数据库。Redis数据操作主要…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

