《程序员面试金典(第6版)》 面试题 08.11. 硬币(动态规划,组合问题,C++)
题目描述
硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)
示例1:
- 输入: n = 5
输出:2
解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1
示例2:
- 输入: n = 10
输出:4
解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1
说明:
- 你可以假设:0 <= n (总金额) <= 1000000
解题思路与代码
这道题我拿到手上,就有了一种拿动态规划去解决它的冲动。所以让我们来看看这道题拿动态规划怎么去解决。
方法一 :动态规划
第一步,拿到这道题,先分析dp数组的下标以及含义是什么?
- 定义一个一维数组dp,其中dp[i]表示组成金额n的钱的不同表示方法的数量。
第二步,去确定状态转移方程式什么?
- 对于每一个币值(1,5,10,25),
依次从当前硬币的价值处开始遍历直到最大金额n处停止,一共有多少种方法,那么对于当前金额j,可以得出递推公式:dp[j] = (dp[j] + dp[j - 当前币值]) % 1000000007
第三步,去初始化dp数组
- 由于下一步的结果永远都是由上一步所去推出来的,所以我们要直到第一步的数值是多少,才好去做下面的推导
- 我们要将初始化dp[0]为1,因为有一种表示方法是使用0个硬币组成0分。其余元素初始化为0。
第四步,确定如何遍历dp数组。
- 我们要用一个双层的for循环去遍历这个dp数组,这是因为,我们一共有4种硬币的面值。所以我们要一次选择每一种面值的数额去作为其实遍历的点,直到达到题目要求的n时停止。
- 那么代码大概就是这样:
for(int& coin : coins)for(int i = coin; i < n+1; ++i)dp[i] = (dp[i] + dp[i - coin])%MOD;
第五步,举例推导dp数组
- 这一步自己在纸上画一画就好了
具体的解决代码如下:
class Solution {
public:int waysToChange(int n) {int MOD = 1000000007;vector<int> dp(n+1);vector<int> coins{1,5,10,25};dp[0] = 1;for(int& coin : coins)for(int i = coin; i < n+1; ++i)dp[i] = (dp[i] + dp[i - coin])%MOD;return dp[n];}
};

复杂度分析
时间复杂度:O(n),其中n为输入金额。这是因为代码中有两层循环,第一层循环遍历硬币,它是一个常数4(币值:1, 5, 10, 25),第二层循环遍历所有金额,从硬币面值到n。因此,总时间复杂度是O(4n),可以简化为O(n)。
空间复杂度:O(n),其中n为输入金额。代码中主要的空间消耗来自dp数组,它的大小为n + 1。因此,空间复杂度为O(n)。
总结
这道题是动态规划里的一道组合类问题。我尝试着把这道题往0-1背包去靠,结果有点费劲。不如就像我这么去解释。
不要硬生生的划分给0-1背包,这就是一道动态规划的组合问题而已。
难度确实始终,也很好理解。但你要往0-1背包去靠,那就很难理解了。我个人感觉。
相关文章:

《程序员面试金典(第6版)》 面试题 08.11. 硬币(动态规划,组合问题,C++)
题目描述 硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007) 示例1: 输入: n 5 输出:2 解释: 有两种方式可以凑成总金额: 55 511111 示例2: 输…...
实体商家做抖音运营如何做矩阵?
商家实体门店如何做好短视频矩阵?这是一个值得深入探讨的问题。在当今的数字化时代,短视频成为越来越多企业吸引用户、提高曝光度的一种重要方式,实体店也不例外。在本文中,我们将提供一些实用的建议,帮助实体店如何做…...
java 双列集合Map 万字详解
目录 一、前言 二、概述 三、特点 四、常用方法 1. V put(K key, V value) : Δ代码演示 : 2. V get(Object key) : Δ代码演示 : 3. V remove(Object key) : Δ代码演示 : 4. int size() : Δ代码演示 : 5. default V replace(K key, V value) : Δ代码演示 : 6. bo…...
【数据结构】二叉树<遍历>
【二叉树遍历】|-前序-中序-后序-层序-|<二叉树的遍历>1.前序遍历【递归】2.中序遍历【递归】3.后序遍历【递归】4.层序遍历【非递归】4.1判断是否是完全二叉树<二叉树的遍历> 在学习二叉树遍历之前我们先了解下二叉树的概念。 二叉树是: 1.空树 2.非空…...

linux查看硬件信息
dmidecode用于在linux下获取硬件信息,遵循SMBIOS/DMI标准,可获取包括BIOS、系统、主板、处理器、内存、缓存等等硬件信息 1、查看CPU信息cat /proc/cpuinfo、lscpu 型号:cat /proc/cpuinfo|grep name|cut -f2 -d:|uniq -c 物理核:…...

吐血整理,互联网大厂最常见的 1120 道 Java 面试题(带答案)整理
前言 作为一个 Java 程序员,你平时总是陷在业务开发里,每天噼里啪啦忙敲着代码,上到系统开发,下到 Bug 修改,你感觉自己无所不能。然而偶尔的一次聚会,你听说和自己一起出道的同学早已经年薪 50 万&#x…...
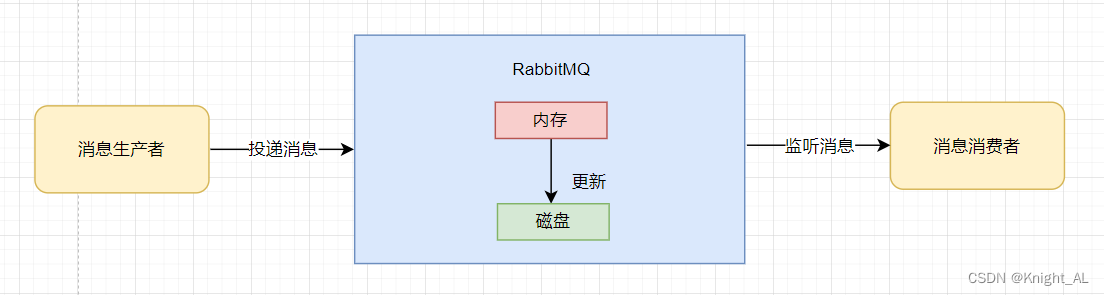
RabbitMQ如何避免消息丢失
目录1.生产者没有成功把消息发送到MQ2.RabbitMQ接收到消息之后丢失了消息3.消费者弄丢了消息前言 首先明确一点一条消息的传送流程:生产者->MQ->消费者 我们根据这三个依次讨论 1.生产者没有成功把消息发送到MQ 丢失的原因:因为网络传输的不稳定…...
)
做算法题的正确姿势(不断更新)
不停的反思自己,总结建议 做一道算法题,不能去死磕。 如果看一道题,半小时内,没有清晰的思路,就看题解!!!你可能觉得你有点思路,就往里死钻,结果可能就像进…...

p85 CTF夺旗-JAVA考点反编译XXE反序列化
数据来源 图片来源 Java 常考点及出题思路 考点技术:xxe,spel 表达式,反序列化,文件安全,最新框架插件漏洞等 设法间接给出源码或相关配置提示文件,间接性源码或直接源码体现等形式 https://www.cnblog…...

FastJson——JSO字符串与对象的相互转化
一、FastJson介绍 Fastjson是阿里巴巴的开源SON解析库它可以解析JSON格式的字符串,支持将java Bean序列化为ISON字符串,也可以从JSON字符串反序列化到JavaBean。 Fastjson的优点 速度快 fastjson相对其他JSON库的特点是快,从2011年fastj…...
《程序员面试金典(第6版)》面试题 08.08. 有重复字符串的排列组合(回溯算法,全排列问题)C++
题目描述 有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。 示例1: 输入:S “qqe” 输出:[“eqq”,“qeq”,“qqe”] 示例2: 输入:S “ab” 输出:[“ab”, “ba”] 提示: 字符都是英文字母。…...

k8s API限流——server级别整体限流和客户端限流
1. 背景 为了防止突发流量影响apiserver可用性,k8s支持多种限流配置,包括: MaxInFlightLimit,server级别整体限流Client限流EventRateLimit, 限制eventAPF,更细力度的限制配置 1.1 MaxInFlightLimit限流 apiserver…...

在华为做了三年软件测试被裁了,我该怎么办
近年来,随着经济环境的变化和企业战略的调整,员工被裁员的情况变得越来越普遍。无论是因为企业经营困难还是因为业务调整,员工们都可能面临被裁员的风险。如果你也遇到了这样的情况,那么你应该怎么办呢? 首先…...

Spring cloud 限流的多种方式
在频繁的网络请求时,服务有时候也会受到很大的压力,尤其是那种网络攻击,非法的。这样的情形有时候需要作一些限制。本文主要介绍了两种限流方法,感兴趣的可以了解一下 目录 一、实战基于 Spring cloud Gateway 的限流 二、基于阿…...
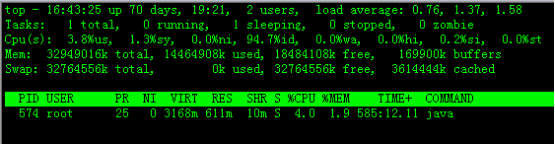
Linux命令·top
top命令是Linux下常用的性能分析工具,能够实时显示系统中各个进程的资源占用状况,类似于Windows的任务管理器。下面详细介绍它的使用方法。top是一个动态显示过程,即可以通过用户按键来不断刷新当前状态.如果在前台执行该命令,它将独占前台,直到用户终止…...

springmvc之系列文章
springmvc之编程步骤 springmvc初始化过程 用WebServlet和WebFilter干掉web.xml 没有web.xml怎么写web程序 一次GET请求在springmvc中是的处理流程 springMVC的handler都有哪些类型 springmvc主要组件简单介绍 springmvc 的Servlet WebApplicationContext springmvc 的…...
)
Matlab实现深度学习(附上完整仿真源码)
文章目录简单案例完整仿真代码下载简单案例 深度学习是一种能够自动学习和提取数据特征的机器学习方法,它已经在图像识别、语音识别、自然语言处理等领域取得了显著的成果。而Matlab作为一个强大的数学计算工具,也提供了丰富的深度学习工具箱࿰…...
我的谷歌书签
Form 表单 | Element Plusa Vue 3 based component library for designers and developershttps://element-plus.gitee.io/zh-CN/component/form.html#%E5%AF%B9%E9%BD%90%E6%96%B9%E5%BC%8F three.js exampleshttp://www.yanhuangxueyuan.com/threejs/examples/#software_geo…...
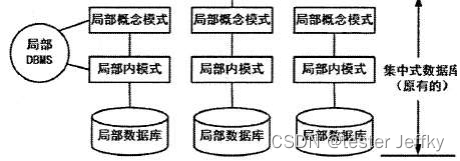
day3 数据库技术考点汇总
一、重点知识点 基本概念:三级模式-两级映像、数据库设计数据库模型:E-R模型、关系模型、关系代数(结合SQL语言)规范化:函数依赖、健与约束、范式、模式分解事务并发:并发三种问题、三级封锁协议数据库新技…...
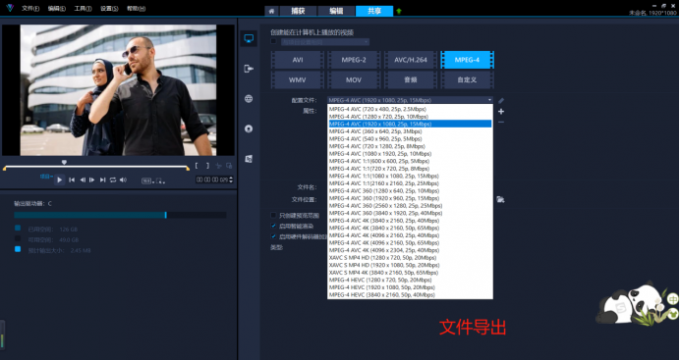
学剪辑难吗 如何使用会声会影2023做剪辑视频
很多剪辑初学者都问过一个问题,学剪辑难吗?其实不论学什么,只要用心学都不难,今天我们就来讲讲如何学做剪辑视频,感兴趣的小伙伴们不要走开!一、学剪辑难吗 其实学剪辑并不是件难事,但是需要掌握…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
