Leetcode: 0001-0010题速览
Leetcode: 0001-0010题速览
本文材料来自于LeetCode solutions in any programming language | 多种编程语言实现 LeetCode、《剑指 Offer(第 2 版)》、《程序员面试金典(第 6 版)》题解
遵从开源协议为知识共享 版权归属-相同方式共享 4.0 国际 公共许可证
研一在读备战就业,制此集合便于空闲时间浏览,有任何疑惑问题欢迎讨论,共同进步
目录
- Leetcode: 0001-0010题速览
- [1. 两数之和](https://leetcode.cn/problems/two-sum)
- 题目描述
- 解法
- 方法一:哈希表
- Python3
- Java
- C++
- [2. 两数相加](https://leetcode.cn/problems/add-two-numbers)
- 题目描述
- 解法
- 方法一:模拟
- Python3
- Java
- C++
- [3. 无重复字符的最长子串](https://leetcode.cn/problems/longest-substring-without-repeating-characters)
- 题目描述
- 解法
- 方法一:双指针 + 哈希表
- Python3
- Java
- C++
- [4. 寻找两个正序数组的中位数](https://leetcode.cn/problems/median-of-two-sorted-arrays)
- 题目描述
- 解法
- 方法一:分治
- Python3
- Java
- C++
- [5. 最长回文子串](https://leetcode.cn/problems/longest-palindromic-substring)
- 题目描述
- 解法
- 方法一:动态规划
- Python3
- Java
- C++
- [6. Z 字形变换](https://leetcode.cn/problems/zigzag-conversion)
- 题目描述
- 解法
- 方法一:模拟
- Python3
- Java
- C++
- [7. 整数反转](https://leetcode.cn/problems/reverse-integer)
- 题目描述
- 解法
- 方法一:数学
- Python3
- Java
- C++
- [8. 字符串转换整数 (atoi)](https://leetcode.cn/problems/string-to-integer-atoi)
- 题目描述
- 解法
- 方法一:遍历字符串
- Python3
- Java
- [9. 回文数](https://leetcode.cn/problems/palindrome-number)
- 题目描述
- 解法
- 方法一:反转一半数字
- Python3
- Java
- C++
- [10. 正则表达式匹配](https://leetcode.cn/problems/regular-expression-matching)
- 题目描述
- 解法
- 方法一:记忆化搜索
- Python3
- Java
- C++
1. 两数之和
题目描述
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104-109 <= nums[i] <= 109-109 <= target <= 109- 只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
难度:简单
标签:数组,哈希表
解法
方法一:哈希表
我们可以使用一个哈希表 d \textit{d} d 来存储每个元素及其对应的索引。
遍历数组 nums \textit{nums} nums,对于当前元素 nums [ i ] \textit{nums}[i] nums[i],我们首先判断 target − nums [ i ] \textit{target} - \textit{nums}[i] target−nums[i] 是否在哈希表 d \textit{d} d 中,如果在 d \textit{d} d 中,说明 target \textit{target} target 值已经找到,返回 target − nums [ i ] \textit{target} - \textit{nums}[i] target−nums[i] 的索引和 i i i 即可。
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n),其中 n n n 为数组 nums \textit{nums} nums 的长度。
Python3
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:d = {}for i, x in enumerate(nums):y = target - xif y in d:return [d[y], i]d[x] = i
Java
class Solution {public int[] twoSum(int[] nums, int target) {Map<Integer, Integer> d = new HashMap<>();for (int i = 0;; ++i) {int x = nums[i];int y = target - x;if (d.containsKey(y)) {return new int[] {d.get(y), i};}d.put(x, i);}}
}
C++
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int, int> d;for (int i = 0;; ++i) {int x = nums[i];int y = target - x;if (d.contains(y)) {return {d[y], i};}d[x] = i;}}
};
2. 两数相加
题目描述
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:

输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
难度:中等
标签:递归,链表,数学
解法
方法一:模拟
我们同时遍历两个链表 l 1 l_1 l1 和 l 2 l_2 l2,并使用变量 c a r r y carry carry 表示当前是否有进位。
每次遍历时,我们取出对应链表的当前位,计算它们与进位 c a r r y carry carry 的和,然后更新进位的值,最后将当前位的值加入答案链表。如果两个链表都遍历完了,并且进位为 0 0 0 时,遍历结束。
最后我们返回答案链表的头节点即可。
时间复杂度 O ( max ( m , n ) ) O(\max(m, n)) O(max(m,n)),其中 m m m 和 n n n 分别为两个链表的长度。我们需要遍历两个链表的全部位置,而处理每个位置只需要 O ( 1 ) O(1) O(1) 的时间。忽略答案的空间消耗,空间复杂度 O ( 1 ) O(1) O(1)。
Python3
## Definition for singly-linked list.
## class ListNode:
## def __init__(self, val=0, next=None):
## self.val = val
## self.next = next
class Solution:def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:dummy = ListNode()carry, curr = 0, dummywhile l1 or l2 or carry:s = (l1.val if l1 else 0) + (l2.val if l2 else 0) + carrycarry, val = divmod(s, 10)curr.next = ListNode(val)curr = curr.nextl1 = l1.next if l1 else Nonel2 = l2.next if l2 else Nonereturn dummy.next
Java
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode dummy = new ListNode(0);int carry = 0;ListNode cur = dummy;while (l1 != null || l2 != null || carry != 0) {int s = (l1 == null ? 0 : l1.val) + (l2 == null ? 0 : l2.val) + carry;carry = s / 10;cur.next = new ListNode(s % 10);cur = cur.next;l1 = l1 == null ? null : l1.next;l2 = l2 == null ? null : l2.next;}return dummy.next;}
}
C++
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode* dummy = new ListNode();int carry = 0;ListNode* cur = dummy;while (l1 || l2 || carry) {int s = (l1 ? l1->val : 0) + (l2 ? l2->val : 0) + carry;carry = s / 10;cur->next = new ListNode(s % 10);cur = cur->next;l1 = l1 ? l1->next : nullptr;l2 = l2 ? l2->next : nullptr;}return dummy->next;}
};
3. 无重复字符的最长子串
题目描述
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104s由英文字母、数字、符号和空格组成
难度:中等
标签:哈希表,字符串,滑动窗口
解法
方法一:双指针 + 哈希表
定义一个哈希表记录当前窗口内出现的字符,记 i i i 和 j j j 分别表示不重复子串的开始位置和结束位置,无重复字符子串的最大长度记为 ans。
遍历字符串 s 的每个字符 s [ j ] s[j] s[j],我们记为 c c c。若 s [ i . . j − 1 ] s[i..j-1] s[i..j−1] 窗口内存在 c c c,则 i i i 循环向右移动,更新哈希表,直至 s [ i . . j − 1 ] s[i..j-1] s[i..j−1] 窗口不存在 c,循环结束。将 c 加入哈希表中,此时 s [ i . . j ] s[i..j] s[i..j] 窗口内不含重复元素,更新 ans 的最大值。
最后返回 ans 即可。
时间复杂度 O ( n ) O(n) O(n),其中 n n n 表示字符串 s 的长度。
双指针算法模板:
for (int i = 0, j = 0; i < n; ++i) {while (j < i && check(j, i)) {++j;}// 具体问题的逻辑
}
Python3
class Solution:def lengthOfLongestSubstring(self, s: str) -> int:ss = set()ans = i = 0for j, c in enumerate(s):while c in ss:ss.remove(s[i])i += 1ss.add(c)ans = max(ans, j - i + 1)return ans
Java
class Solution {public int lengthOfLongestSubstring(String s) {boolean[] ss = new boolean[128];int ans = 0;for (int i = 0, j = 0; j < s.length(); ++j) {char c = s.charAt(j);while (ss[c]) {ss[s.charAt(i++)] = false;}ss[c] = true;ans = Math.max(ans, j - i + 1);}return ans;}
}
C++
class Solution {
public:int lengthOfLongestSubstring(string s) {bool ss[128]{};int ans = 0;for (int i = 0, j = 0; j < s.size(); ++j) {while (ss[s[j]]) {ss[s[i++]] = false;}ss[s[j]] = true;ans = max(ans, j - i + 1);}return ans;}
};
4. 寻找两个正序数组的中位数
题目描述
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
难度:困难
标签:数组,二分查找,分治
解法
方法一:分治
题目要求算法的时间复杂度为 O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n)),因此不能直接遍历两个数组,而是需要使用二分查找的方法。
如果 m + n m + n m+n 是奇数,那么中位数就是第 ⌊ m + n + 1 2 ⌋ \left\lfloor\frac{m + n + 1}{2}\right\rfloor ⌊2m+n+1⌋ 个数;如果 m + n m + n m+n 是偶数,那么中位数就是第 ⌊ m + n + 1 2 ⌋ \left\lfloor\frac{m + n + 1}{2}\right\rfloor ⌊2m+n+1⌋ 和第 ⌊ m + n + 2 2 ⌋ \left\lfloor\frac{m + n + 2}{2}\right\rfloor ⌊2m+n+2⌋ 个数的平均数。实际上,我们可以统一为求第 ⌊ m + n + 1 2 ⌋ \left\lfloor\frac{m + n + 1}{2}\right\rfloor ⌊2m+n+1⌋ 个数和第 ⌊ m + n + 2 2 ⌋ \left\lfloor\frac{m + n + 2}{2}\right\rfloor ⌊2m+n+2⌋ 个数的平均数。
因此,我们可以设计一个函数 f ( i , j , k ) f(i, j, k) f(i,j,k),表示在数组 n u m s 1 nums1 nums1 的区间 [ i , m ) [i, m) [i,m) 和数组 n u m s 2 nums2 nums2 的区间 [ j , n ) [j, n) [j,n) 中,求第 k k k 小的数。那么中位数就是 f ( 0 , 0 , ⌊ m + n + 1 2 ⌋ ) f(0, 0, \left\lfloor\frac{m + n + 1}{2}\right\rfloor) f(0,0,⌊2m+n+1⌋) 和 f ( 0 , 0 , ⌊ m + n + 2 2 ⌋ ) f(0, 0, \left\lfloor\frac{m + n + 2}{2}\right\rfloor) f(0,0,⌊2m+n+2⌋) 的平均数。
函数 f ( i , j , k ) f(i, j, k) f(i,j,k) 的实现思路如下:
- 如果 i ≥ m i \geq m i≥m,说明数组 n u m s 1 nums1 nums1 的区间 [ i , m ) [i, m) [i,m) 为空,因此直接返回 n u m s 2 [ j + k − 1 ] nums2[j + k - 1] nums2[j+k−1];
- 如果 j ≥ n j \geq n j≥n,说明数组 n u m s 2 nums2 nums2 的区间 [ j , n ) [j, n) [j,n) 为空,因此直接返回 n u m s 1 [ i + k − 1 ] nums1[i + k - 1] nums1[i+k−1];
- 如果 k = 1 k = 1 k=1,说明要找第一个数,因此只需要返回 n u m s 1 [ i ] nums1[i] nums1[i] 和 n u m s 2 [ j ] nums2[j] nums2[j] 中的最小值;
- 否则,我们分别在两个数组中查找第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数,设为 x x x 和 y y y。(注意,如果某个数组不存在第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数,那么我们将第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数视为 + ∞ +\infty +∞。)比较 x x x 和 y y y 的大小:
- 如果 x ≤ y x \leq y x≤y,则说明数组 n u m s 1 nums1 nums1 的第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数不可能是第 k k k 小的数,因此我们可以排除数组 n u m s 1 nums1 nums1 的区间 [ i , i + ⌊ k 2 ⌋ ) [i, i + \left\lfloor\frac{k}{2}\right\rfloor) [i,i+⌊2k⌋),递归调用 f ( i + ⌊ k 2 ⌋ , j , k − ⌊ k 2 ⌋ ) f(i + \left\lfloor\frac{k}{2}\right\rfloor, j, k - \left\lfloor\frac{k}{2}\right\rfloor) f(i+⌊2k⌋,j,k−⌊2k⌋)。
- 如果 x > y x > y x>y,则说明数组 n u m s 2 nums2 nums2 的第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数不可能是第 k k k 小的数,因此我们可以排除数组 n u m s 2 nums2 nums2 的区间 [ j , j + ⌊ k 2 ⌋ ) [j, j + \left\lfloor\frac{k}{2}\right\rfloor) [j,j+⌊2k⌋),递归调用 f ( i , j + ⌊ k 2 ⌋ , k − ⌊ k 2 ⌋ ) f(i, j + \left\lfloor\frac{k}{2}\right\rfloor, k - \left\lfloor\frac{k}{2}\right\rfloor) f(i,j+⌊2k⌋,k−⌊2k⌋)。
时间复杂度 O ( log ( m + n ) ) O(\log(m + n)) O(log(m+n)),空间复杂度 O ( log ( m + n ) ) O(\log(m + n)) O(log(m+n))。其中 m m m 和 n n n 分别是数组 n u m s 1 nums1 nums1 和 n u m s 2 nums2 nums2 的长度。
Python3
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:def f(i: int, j: int, k: int) -> int:if i >= m:return nums2[j + k - 1]if j >= n:return nums1[i + k - 1]if k == 1:return min(nums1[i], nums2[j])p = k // 2x = nums1[i + p - 1] if i + p - 1 < m else infy = nums2[j + p - 1] if j + p - 1 < n else infreturn f(i + p, j, k - p) if x < y else f(i, j + p, k - p)m, n = len(nums1), len(nums2)a = f(0, 0, (m + n + 1) // 2)b = f(0, 0, (m + n + 2) // 2)return (a + b) / 2
Java
class Solution {private int m;private int n;private int[] nums1;private int[] nums2;public double findMedianSortedArrays(int[] nums1, int[] nums2) {m = nums1.length;n = nums2.length;this.nums1 = nums1;this.nums2 = nums2;int a = f(0, 0, (m + n + 1) / 2);int b = f(0, 0, (m + n + 2) / 2);return (a + b) / 2.0;}private int f(int i, int j, int k) {if (i >= m) {return nums2[j + k - 1];}if (j >= n) {return nums1[i + k - 1];}if (k == 1) {return Math.min(nums1[i], nums2[j]);}int p = k / 2;int x = i + p - 1 < m ? nums1[i + p - 1] : 1 << 30;int y = j + p - 1 < n ? nums2[j + p - 1] : 1 << 30;return x < y ? f(i + p, j, k - p) : f(i, j + p, k - p);}
}
C++
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size(), n = nums2.size();function<int(int, int, int)> f = [&](int i, int j, int k) {if (i >= m) {return nums2[j + k - 1];}if (j >= n) {return nums1[i + k - 1];}if (k == 1) {return min(nums1[i], nums2[j]);}int p = k / 2;int x = i + p - 1 < m ? nums1[i + p - 1] : 1 << 30;int y = j + p - 1 < n ? nums2[j + p - 1] : 1 << 30;return x < y ? f(i + p, j, k - p) : f(i, j + p, k - p);};int a = f(0, 0, (m + n + 1) / 2);int b = f(0, 0, (m + n + 2) / 2);return (a + b) / 2.0;}
};
5. 最长回文子串
题目描述
给你一个字符串 s,找到 s 中最长的 回文 子串。
示例 1:
输入:s = “babad”
输出:“bab”
解释:“aba” 同样是符合题意的答案。
示例 2:
输入:s = “cbbd”
输出:“bb”
提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
难度:中等
标签:双指针,字符串,动态规划
解法
方法一:动态规划
我们定义 f [ i ] [ j ] f[i][j] f[i][j] 表示字符串 s [ i . . j ] s[i..j] s[i..j] 是否为回文串,初始时 f [ i ] [ j ] = t r u e f[i][j] = true f[i][j]=true。
接下来,我们定义变量 k k k 和 m x mx mx,其中 k k k 表示最长回文串的起始位置, m x mx mx 表示最长回文串的长度。初始时 k = 0 k = 0 k=0, m x = 1 mx = 1 mx=1。
考虑 f [ i ] [ j ] f[i][j] f[i][j],如果 s [ i ] = s [ j ] s[i] = s[j] s[i]=s[j],那么 f [ i ] [ j ] = f [ i + 1 ] [ j − 1 ] f[i][j] = f[i + 1][j - 1] f[i][j]=f[i+1][j−1];否则 f [ i ] [ j ] = f a l s e f[i][j] = false f[i][j]=false。如果 f [ i ] [ j ] = t r u e f[i][j] = true f[i][j]=true 并且 m x < j − i + 1 mx \lt j - i + 1 mx<j−i+1,那么我们更新 k = i k = i k=i, m x = j − i + 1 mx = j - i + 1 mx=j−i+1。
由于 f [ i ] [ j ] f[i][j] f[i][j] 依赖于 f [ i + 1 ] [ j − 1 ] f[i + 1][j - 1] f[i+1][j−1],因此我们需要保证 i + 1 i + 1 i+1 在 j − 1 j - 1 j−1 之前,因此我们需要从大到小地枚举 i i i,从小到大地枚举 j j j。
时间复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( n 2 ) O(n^2) O(n2)。其中 n n n 是字符串 s s s 的长度。
Python3
class Solution:def longestPalindrome(self, s: str) -> str:n = len(s)f = [[True] * n for _ in range(n)]k, mx = 0, 1for i in range(n - 2, -1, -1):for j in range(i + 1, n):f[i][j] = Falseif s[i] == s[j]:f[i][j] = f[i + 1][j - 1]if f[i][j] and mx < j - i + 1:k, mx = i, j - i + 1return s[k : k + mx]
Java
class Solution {public String longestPalindrome(String s) {int n = s.length();boolean[][] f = new boolean[n][n];for (var g : f) {Arrays.fill(g, true);}int k = 0, mx = 1;for (int i = n - 2; i >= 0; --i) {for (int j = i + 1; j < n; ++j) {f[i][j] = false;if (s.charAt(i) == s.charAt(j)) {f[i][j] = f[i + 1][j - 1];if (f[i][j] && mx < j - i + 1) {mx = j - i + 1;k = i;}}}}return s.substring(k, k + mx);}
}
C++
class Solution {
public:string longestPalindrome(string s) {int n = s.size();vector<vector<bool>> f(n, vector<bool>(n, true));int k = 0, mx = 1;for (int i = n - 2; ~i; --i) {for (int j = i + 1; j < n; ++j) {f[i][j] = false;if (s[i] == s[j]) {f[i][j] = f[i + 1][j - 1];if (f[i][j] && mx < j - i + 1) {mx = j - i + 1;k = i;}}}}return s.substr(k, mx);}
};
6. Z 字形变换
题目描述
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = “PAYPALISHIRING”, numRows = 3
输出:“PAHNAPLSIIGYIR”
示例 2:
输入:s = “PAYPALISHIRING”, numRows = 4
输出:“PINALSIGYAHRPI”
解释:
P I N
A L S I G
Y A H R
P I
示例 3:
输入:s = “A”, numRows = 1
输出:“A”
提示:
1 <= s.length <= 1000s由英文字母(小写和大写)、','和'.'组成1 <= numRows <= 1000
难度:中等
标签:字符串
解法
方法一:模拟
我们用一个二维数组 g g g 来模拟 Z Z Z 字形排列的过程,其中 g [ i ] [ j ] g[i][j] g[i][j] 表示第 i i i 行第 j j j 列的字符。初始时 i = 0 i=0 i=0,另外我们定义一个方向变量 k k k,初始时 k = − 1 k=-1 k=−1,表示向上走。
我们从左到右遍历字符串 s s s,每次遍历到一个字符 c c c,将其追加到 g [ i ] g[i] g[i] 中,如果此时 i = 0 i=0 i=0 或者 i = n u m R o w s − 1 i=numRows-1 i=numRows−1,说明当前字符位于 Z Z Z 字形排列的拐点,我们将 k k k 的值反转,即 k = − k k=-k k=−k。接下来,我们将 i i i 的值更新为 i + k i+k i+k,即向上或向下移动一行。继续遍历下一个字符,直到遍历完字符串 s s s,我们返回 g g g 中所有行拼接后的字符串即可。
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)。其中 n n n 为字符串 s s s 的长度。
Python3
class Solution:def convert(self, s: str, numRows: int) -> str:if numRows == 1:return sg = [[] for _ in range(numRows)]i, k = 0, -1for c in s:g[i].append(c)if i == 0 or i == numRows - 1:k = -ki += kreturn ''.join(chain(*g))
Java
class Solution {public String convert(String s, int numRows) {if (numRows == 1) {return s;}StringBuilder[] g = new StringBuilder[numRows];Arrays.setAll(g, k -> new StringBuilder());int i = 0, k = -1;for (char c : s.toCharArray()) {g[i].append(c);if (i == 0 || i == numRows - 1) {k = -k;}i += k;}return String.join("", g);}
}
C++
class Solution {
public:string convert(string s, int numRows) {if (numRows == 1) {return s;}vector<string> g(numRows);int i = 0, k = -1;for (char c : s) {g[i] += c;if (i == 0 || i == numRows - 1) {k = -k;}i += k;}string ans;for (auto& t : g) {ans += t;}return ans;}
};
7. 整数反转
题目描述
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
示例 1:
输入:x = 123
输出:321
示例 2:
输入:x = -123
输出:-321
示例 3:
输入:x = 120
输出:21
示例 4:
输入:x = 0
输出:0
提示:
-231 <= x <= 231 - 1
难度:中等
标签:数学
解法
方法一:数学
我们不妨记 m i mi mi 和 m x mx mx 分别为 − 2 31 -2^{31} −231 和 2 31 − 1 2^{31} - 1 231−1,则 x x x 的反转结果 a n s ans ans 需要满足 m i ≤ a n s ≤ m x mi \le ans \le mx mi≤ans≤mx。
我们可以通过不断地对 x x x 取余来获取 x x x 的最后一位数字 y y y,并将 y y y 添加到 a n s ans ans 的末尾。在添加 y y y 之前,我们需要判断 a n s ans ans 是否溢出。即判断 a n s × 10 + y ans \times 10 + y ans×10+y 是否在 [ m i , m x ] [mi, mx] [mi,mx] 的范围内。
若 x > 0 x \gt 0 x>0,那么需要满足 a n s × 10 + y ≤ m x ans \times 10 + y \leq mx ans×10+y≤mx,即 a n s × 10 + y ≤ ⌊ m x 10 ⌋ × 10 + 7 ans \times 10 + y \leq \left \lfloor \frac{mx}{10} \right \rfloor \times 10 + 7 ans×10+y≤⌊10mx⌋×10+7。整理得 ( a n s − ⌊ m x 10 ⌋ ) × 10 ≤ 7 − y (ans - \left \lfloor \frac{mx}{10} \right \rfloor) \times 10 \leq 7 - y (ans−⌊10mx⌋)×10≤7−y。
下面我们讨论上述不等式成立的条件:
- 当 a n s < ⌊ m x 10 ⌋ ans \lt \left \lfloor \frac{mx}{10} \right \rfloor ans<⌊10mx⌋ 时,不等式显然成立;
- 当 a n s = ⌊ m x 10 ⌋ ans = \left \lfloor \frac{mx}{10} \right \rfloor ans=⌊10mx⌋ 时,不等式成立的充要条件是 y ≤ 7 y \leq 7 y≤7。如果 a n s = ⌊ m x 10 ⌋ ans = \left \lfloor \frac{mx}{10} \right \rfloor ans=⌊10mx⌋ 并且还能继续添加数字,说明此时数字是最高位,即此时 y y y 一定不超过 2 2 2,因此,不等式一定成立;
- 当 a n s > ⌊ m x 10 ⌋ ans \gt \left \lfloor \frac{mx}{10} \right \rfloor ans>⌊10mx⌋ 时,不等式显然不成立。
综上,当 x > 0 x \gt 0 x>0 时,不等式成立的充要条件是 a n s ≤ ⌊ m x 10 ⌋ ans \leq \left \lfloor \frac{mx}{10} \right \rfloor ans≤⌊10mx⌋。
同理,当 x < 0 x \lt 0 x<0 时,不等式成立的充要条件是 a n s ≥ ⌊ m i 10 ⌋ ans \geq \left \lfloor \frac{mi}{10} \right \rfloor ans≥⌊10mi⌋。
因此,我们可以通过判断 a n s ans ans 是否在 [ ⌊ m i 10 ⌋ , ⌊ m x 10 ⌋ ] [\left \lfloor \frac{mi}{10} \right \rfloor, \left \lfloor \frac{mx}{10} \right \rfloor] [⌊10mi⌋,⌊10mx⌋] 的范围内来判断 a n s ans ans 是否溢出。若溢出,则返回 0 0 0。否则,将 y y y 添加到 a n s ans ans 的末尾,然后将 x x x 的最后一位数字去除,即 x ← ⌊ x 10 ⌋ x \gets \left \lfloor \frac{x}{10} \right \rfloor x←⌊10x⌋。
时间复杂度 O ( log ∣ x ∣ ) O(\log |x|) O(log∣x∣),其中 ∣ x ∣ |x| ∣x∣ 为 x x x 的绝对值。空间复杂度 O ( 1 ) O(1) O(1)。
Python3
class Solution:def reverse(self, x: int) -> int:ans = 0mi, mx = -(2**31), 2**31 - 1while x:if ans < mi // 10 + 1 or ans > mx // 10:return 0y = x % 10if x < 0 and y > 0:y -= 10ans = ans * 10 + yx = (x - y) // 10return ans
Java
class Solution {public int reverse(int x) {int ans = 0;for (; x != 0; x /= 10) {if (ans < Integer.MIN_VALUE / 10 || ans > Integer.MAX_VALUE / 10) {return 0;}ans = ans * 10 + x % 10;}return ans;}
}
C++
class Solution {
public:int reverse(int x) {int ans = 0;for (; x; x /= 10) {if (ans < INT_MIN / 10 || ans > INT_MAX / 10) {return 0;}ans = ans * 10 + x % 10;}return ans;}
};
8. 字符串转换整数 (atoi)
题目描述
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数。
函数 myAtoi(string s) 的算法如下:
- 空格:读入字符串并丢弃无用的前导空格(
" ") - 符号:检查下一个字符(假设还未到字符末尾)为
'-'还是'+'。如果两者都不存在,则假定结果为正。 - 转换:通过跳过前置零来读取该整数,直到遇到非数字字符或到达字符串的结尾。如果没有读取数字,则结果为0。
- 舍入:如果整数数超过 32 位有符号整数范围
[−231, 231 − 1],需要截断这个整数,使其保持在这个范围内。具体来说,小于−231的整数应该被舍入为−231,大于231 − 1的整数应该被舍入为231 − 1。
返回整数作为最终结果。
示例 1:
输入:s = "42"
输出:42
解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。
带下划线线的字符是所读的内容,插入符号是当前读入位置。
第 1 步:“42”(当前没有读入字符,因为没有前导空格)
^
第 2 步:“42”(当前没有读入字符,因为这里不存在 ‘-’ 或者 ‘+’)
^
第 3 步:“42”(读入 “42”)
^
示例 2:
输入:s = " -042"
输出:-42
解释:
第 1 步:“ -042”(读入前导空格,但忽视掉)
^
第 2 步:" -042"(读入 ‘-’ 字符,所以结果应该是负数)
^
第 3 步:" -042"(读入 “042”,在结果中忽略前导零)
^
示例 3:
输入:s = "1337c0d3"
输出:1337
解释:
第 1 步:“1337c0d3”(当前没有读入字符,因为没有前导空格)
^
第 2 步:“1337c0d3”(当前没有读入字符,因为这里不存在 ‘-’ 或者 ‘+’)
^
第 3 步:“1337c0d3”(读入 “1337”;由于下一个字符不是一个数字,所以读入停止)
^
示例 4:
输入:s = "0-1"
输出:0
解释:
第 1 步:“0-1” (当前没有读入字符,因为没有前导空格)
^
第 2 步:“0-1” (当前没有读入字符,因为这里不存在 ‘-’ 或者 ‘+’)
^
第 3 步:“0-1” (读入 “0”;由于下一个字符不是一个数字,所以读入停止)
^
示例 5:
输入:s = "words and 987"
输出:0
解释:
读取在第一个非数字字符“w”处停止。
提示:
0 <= s.length <= 200s由英文字母(大写和小写)、数字(0-9)、' '、'+'、'-'和'.'组成
难度:中等
标签:字符串
解法
方法一:遍历字符串
我们首先判断字符串是否为空,如果是,直接返回 0 0 0。
否则,我们需要遍历字符串,跳过前导空格,判断第一个非空格字符是否为正负号。
接着遍历后面的字符,如果是数字,我们判断添加该数字是否会导致整数溢出,如果会,我们根据正负号返回结果。否则我们将数字添加到结果中。继续遍历后面的字符,直到遇到非数字字符或者遍历结束。
遍历结束后,我们根据正负号返回结果。
时间复杂度 O ( n ) O(n) O(n),其中 n n n 为字符串的长度。我们只需要依次处理所有字符。空间复杂度 O ( 1 ) O(1) O(1)。
同面试题 67. 把字符串转换成整数。
Python3
class Solution:def myAtoi(self, s: str) -> int:if not s:return 0n = len(s)if n == 0:return 0i = 0while s[i] == ' ':i += 1# 仅包含空格if i == n:return 0sign = -1 if s[i] == '-' else 1if s[i] in ['-', '+']:i += 1res, flag = 0, (2**31 - 1) // 10while i < n:# 非数字,跳出循环体if not s[i].isdigit():breakc = int(s[i])# 溢出判断if res > flag or (res == flag and c > 7):return 2**31 - 1 if sign > 0 else -(2**31)res = res * 10 + ci += 1return sign * res
Java
class Solution {public int myAtoi(String s) {if (s == null) return 0;int n = s.length();if (n == 0) return 0;int i = 0;while (s.charAt(i) == ' ') {// 仅包含空格if (++i == n) return 0;}int sign = 1;if (s.charAt(i) == '-') sign = -1;if (s.charAt(i) == '-' || s.charAt(i) == '+') ++i;int res = 0, flag = Integer.MAX_VALUE / 10;for (; i < n; ++i) {// 非数字,跳出循环体if (s.charAt(i) < '0' || s.charAt(i) > '9') break;// 溢出判断if (res > flag || (res == flag && s.charAt(i) > '7'))return sign > 0 ? Integer.MAX_VALUE : Integer.MIN_VALUE;res = res * 10 + (s.charAt(i) - '0');}return sign * res;}
}
9. 回文数
题目描述
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
- 例如,
121是回文,而123不是。
示例 1:
输入:x = 121
输出:true
示例 2:
输入:x = -121
输出:false
解释:从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入:x = 10
输出:false
解释:从右向左读, 为 01 。因此它不是一个回文数。
提示:
-231 <= x <= 231 - 1
进阶:你能不将整数转为字符串来解决这个问题吗?
难度:简单
标签:数学
解法
方法一:反转一半数字
我们先判断特殊情况:
- 如果 x < 0 x \lt 0 x<0,那么 x x x 不是回文数,直接返回
false; - 如果 x > 0 x \gt 0 x>0 且 x x x 的个位数是 0 0 0,那么 x x x 不是回文数,直接返回
false; - 如果 x x x 的个位数不是 0 0 0,那么 x x x 可能是回文数,继续执行下面的步骤。
我们将 x x x 的后半部分反转,与前半部分进行比较,如果相等,那么 x x x 是回文数,否则 x x x 不是回文数。
举个例子,例如 x = 1221 x = 1221 x=1221,我们可以将数字后半部分从 “21” 反转为 “12”,并将其与前半部分 “12” 进行比较,因为二者相等,我们得知数字 x x x 是回文。
让我们看看如何将后半部分反转。
对于数字 1221 1221 1221,如果执行 1221 m o d 10 1221 \bmod 10 1221mod10,我们将得到最后一位数字 1 1 1,要得到倒数第二位数字,我们可以先通过除以 10 10 10 将最后一位数字从 1221 1221 1221 中移除, 1221 / 10 = 122 1221 / 10 = 122 1221/10=122,再求出上一步结果除以 10 10 10 的余数, 122 m o d 10 = 2 122 \bmod 10 = 2 122mod10=2,就可以得到倒数第二位数字。
如果继续这个过程,我们将得到更多位数的反转数字。
通过将最后一位数字不断地累乘到取出数字的变量 y y y 上,我们可以得到以相反顺序的数字。
在代码实现上,我们可以反复“取出” x x x 的最后一位数字,并将其“添加”到 y y y 的后面,循环直到 y ≥ x y \ge x y≥x,如果此时 x = y x = y x=y,或者 x = y / 10 x = y / 10 x=y/10,那么 x x x 就是回文数。
时间复杂度 O ( log 10 ( n ) ) O(\log_{10}(n)) O(log10(n)),其中 n n n 是 x x x。对于每次迭代,我们会将输入除以 10 10 10,因此时间复杂度为 O ( log 10 ( n ) ) O(\log_{10}(n)) O(log10(n))。空间复杂度 O ( 1 ) O(1) O(1)。
Python3
class Solution:def isPalindrome(self, x: int) -> bool:if x < 0 or (x and x % 10 == 0):return Falsey = 0while y < x:y = y * 10 + x % 10x //= 10return x in (y, y // 10)
Java
class Solution {public boolean isPalindrome(int x) {if (x < 0 || (x > 0 && x % 10 == 0)) {return false;}int y = 0;for (; y < x; x /= 10) {y = y * 10 + x % 10;}return x == y || x == y / 10;}
}
C++
class Solution {
public:bool isPalindrome(int x) {if (x < 0 || (x && x % 10 == 0)) {return false;}int y = 0;for (; y < x; x /= 10) {y = y * 10 + x % 10;}return x == y || x == y / 10;}
};
10. 正则表达式匹配
题目描述
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s 的,而不是部分字符串。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = “a*”
输出:true
解释:因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:
输入:s = “ab”, p = “."
输出:true
解释:".” 表示可匹配零个或多个(‘*’)任意字符(‘.’)。
提示:
1 <= s.length <= 201 <= p.length <= 20s只包含从a-z的小写字母。p只包含从a-z的小写字母,以及字符.和*。- 保证每次出现字符
*时,前面都匹配到有效的字符
难度:困难
标签:递归,字符串,动态规划
解法
方法一:记忆化搜索
我们设计一个函数 d f s ( i , j ) dfs(i, j) dfs(i,j),表示从 s s s 的第 i i i 个字符开始,和 p p p 的第 j j j 个字符开始是否匹配。那么答案就是 d f s ( 0 , 0 ) dfs(0, 0) dfs(0,0)。
函数 d f s ( i , j ) dfs(i, j) dfs(i,j) 的计算过程如下:
- 如果 j j j 已经到达 p p p 的末尾,那么如果 i i i 也到达了 s s s 的末尾,那么匹配成功,否则匹配失败。
- 如果 j j j 的下一个字符是
'*',我们可以选择匹配 0 0 0 个 s [ i ] s[i] s[i] 字符,那么就是 d f s ( i , j + 2 ) dfs(i, j + 2) dfs(i,j+2)。如果此时 i < m i \lt m i<m 并且 s [ i ] s[i] s[i] 和 p [ j ] p[j] p[j] 匹配,那么我们可以选择匹配 1 1 1 个 s [ i ] s[i] s[i] 字符,那么就是 d f s ( i + 1 , j ) dfs(i + 1, j) dfs(i+1,j)。 - 如果 j j j 的下一个字符不是
'*',那么如果 i < m i \lt m i<m 并且 s [ i ] s[i] s[i] 和 p [ j ] p[j] p[j] 匹配,那么就是 d f s ( i + 1 , j + 1 ) dfs(i + 1, j + 1) dfs(i+1,j+1)。否则匹配失败。
过程中,我们可以使用记忆化搜索,避免重复计算。
时间复杂度 O ( m × n ) O(m \times n) O(m×n),空间复杂度 O ( m × n ) O(m \times n) O(m×n)。其中 m m m 和 n n n 分别是 s s s 和 p p p 的长度。
Python3
class Solution:def isMatch(self, s: str, p: str) -> bool:@cachedef dfs(i, j):if j >= n:return i == mif j + 1 < n and p[j + 1] == '*':return dfs(i, j + 2) or (i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j))return i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j + 1)m, n = len(s), len(p)return dfs(0, 0)
Java
class Solution {private Boolean[][] f;private String s;private String p;private int m;private int n;public boolean isMatch(String s, String p) {m = s.length();n = p.length();f = new Boolean[m + 1][n + 1];this.s = s;this.p = p;return dfs(0, 0);}private boolean dfs(int i, int j) {if (j >= n) {return i == m;}if (f[i][j] != null) {return f[i][j];}boolean res = false;if (j + 1 < n && p.charAt(j + 1) == '*') {res = dfs(i, j + 2)|| (i < m && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.') && dfs(i + 1, j));} else {res = i < m && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.') && dfs(i + 1, j + 1);}return f[i][j] = res;}
}
C++
class Solution {
public:bool isMatch(string s, string p) {int m = s.size(), n = p.size();int f[m + 1][n + 1];memset(f, 0, sizeof f);function<bool(int, int)> dfs = [&](int i, int j) -> bool {if (j >= n) {return i == m;}if (f[i][j]) {return f[i][j] == 1;}int res = -1;if (j + 1 < n && p[j + 1] == '*') {if (dfs(i, j + 2) or (i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j))) {res = 1;}} else if (i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j + 1)) {res = 1;}f[i][j] = res;return res == 1;};return dfs(0, 0);}
};
相关文章:

Leetcode: 0001-0010题速览
Leetcode: 0001-0010题速览 本文材料来自于LeetCode solutions in any programming language | 多种编程语言实现 LeetCode、《剑指 Offer(第 2 版)》、《程序员面试金典(第 6 版)》题解 遵从开源协议为知识共享 版权归属-相同方式…...
计算机的错误计算(一百一十二)
摘要 计算机的错误计算(六十三)与(六十八)以及(六十九)分别探讨了大数与 附近数以及 附近数 的余切函数的计算精度问题。本节讨论余切序列(即迭代 )的计算精度问题。 余切序列是指…...
C++基础(7)——STL简介及string类
目录 1.STL简介 1.1什么是 1.2STL的历史版本 1.3STL的六大组件 编辑 1.4有用的网址 2.string类 2.1string的多种定义方式 2.2string的插入 2.2.1尾插(push_back) 2.2.2insert插入 2.3拼接(append) 2.4删除 2.4.1尾…...

配置Nginx以支持通过HTTPS回源到CDN
要配置Nginx以支持通过HTTPS回源到CDN,你需要确保Nginx已正确配置SSL,并且能够处理来自CDN的HTTPS请求。以下是一个简化的Nginx配置示例,它配置了SSL并设置了代理服务器参数以回源到CDN: server {listen 443 ssl;server_name you…...
yolov10+strongsort的目标跟踪实现
此次yolov10deepsort不论是准确率还是稳定性,再次超越了之前的yolodeepsort系列。 yolov10介绍——实时端到端物体检测 YOLOv10 是清华大学研究人员在 UltralyticsPython 清华大学的研究人员在 YOLOv10软件包的基础上,引入了一种新的实时目标检测…...
C# 字符与字符串
本课要点: 1、字符类Char的使用 2、字符串类String的使用 3、可变字符串****StringBuilder 4、常见错误 一 何时用到字符与字符串 问题: 输出C#**课考试最高分:**98.5 输出最高分学生姓名:张三 输出最高分学生性别&#x…...

在Ubuntu 16.04上使用LEMP安装WordPress的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 WordPress 是互联网上最流行的 CMS(内容管理系统)。它允许您在 MySQL 后端和 PHP 处理的基础上轻松设置灵…...

显示器放大后,大漠识图识色坐标偏移解决方法
原因分析: 显示器分辨率较高,DPI设置放大125% or 150% or 200%,游戏打开时也会默认会根据显示器的放大比例自行放大,但是大漠综合管理工具抓图不会放大; 解决方法: 1、大漠综合管理…...

C++容器之list基本使用
目录 前言 一、list的介绍? 二、使用 1.list的构造 2.list iterator的使用 3.list capacity 🥇 empty 🥇size 4.list element access 🥇 front 🥇 back 5.list modifiers 🥇 push_front 🥇 po…...
Redis-哨兵
概念 Redis Sentinel 相关名词解释 注意: 哨兵机制不负责存储数据,只是对其它的redis-server进程起到监控的作用哨兵节点,也会搞一个集合,防止一个挂了 ⼈⼯恢复主节点故障 用户监控: 实际开发中,对于服务器后端开发,监控程序,是很重要的 服务器长期运行,总会有一些意外,…...
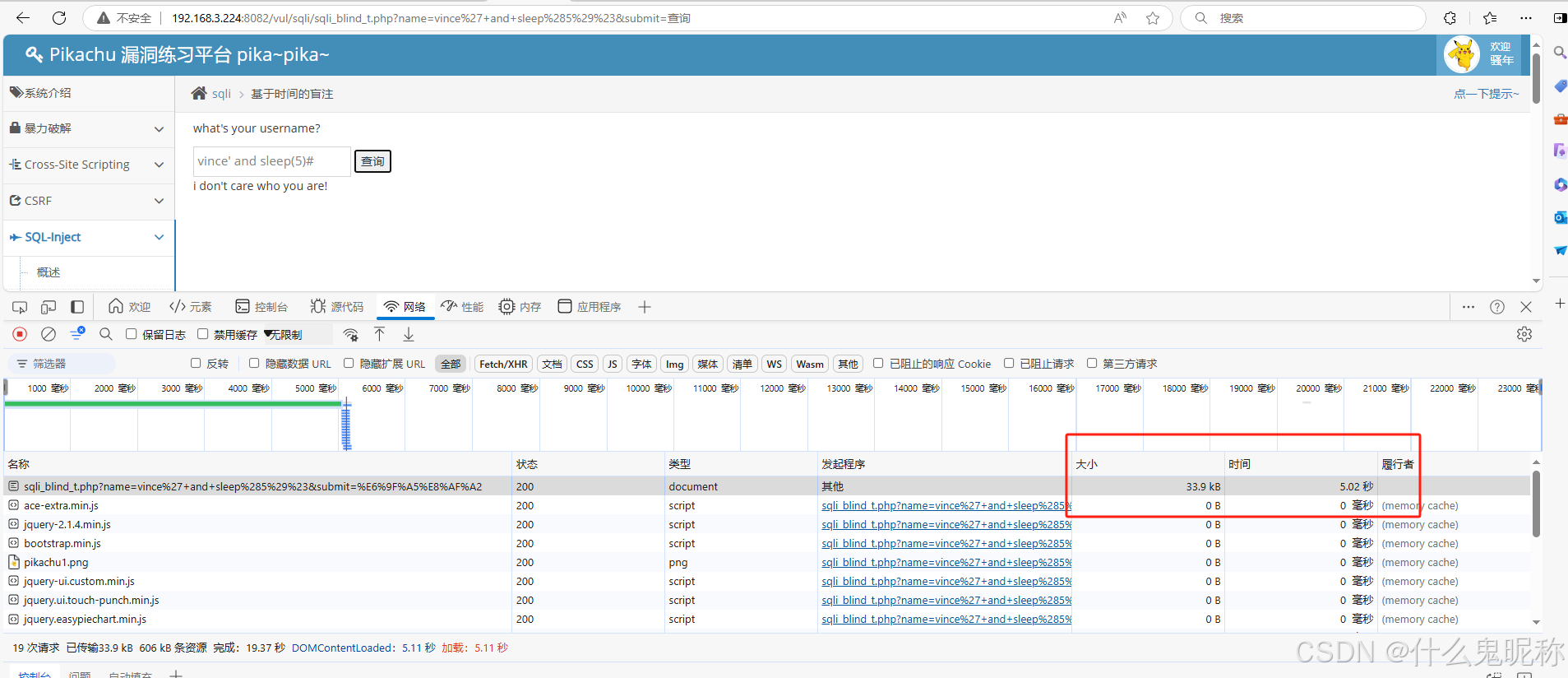
Pikachu-Sql-Inject - 基于时间的盲注
基于时间的盲注: 就是前端的基于time 的盲注,什么错误信息都看不到,但是还可以通过特定的输入,判断后台的执行时间,从而确定注入。 mysql 里函数sleep() 是延时的意思,sleep(10)就是数据库延时10 秒返回内…...

JAVA开源项目 旅游管理系统 计算机毕业设计
本文项目编号 T 063 ,文末自助获取源码 \color{red}{T063,文末自助获取源码} T063,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析5.4 用例设计 六、核…...

景联文科技入选《2024中国AI大模型产业图谱2.0版》数据集代表厂商
近日,大数据产业领域头部媒体数据猿携手上海大数据联盟联合发布了备受瞩目的《2024中国AI大模型产业图谱2.0版》。以大数据与AI为代表的智能技术为主要视角,聚焦全产业链,为业内提供更为专业直观的行业指导。 景联文科技凭借高质量数据集&…...
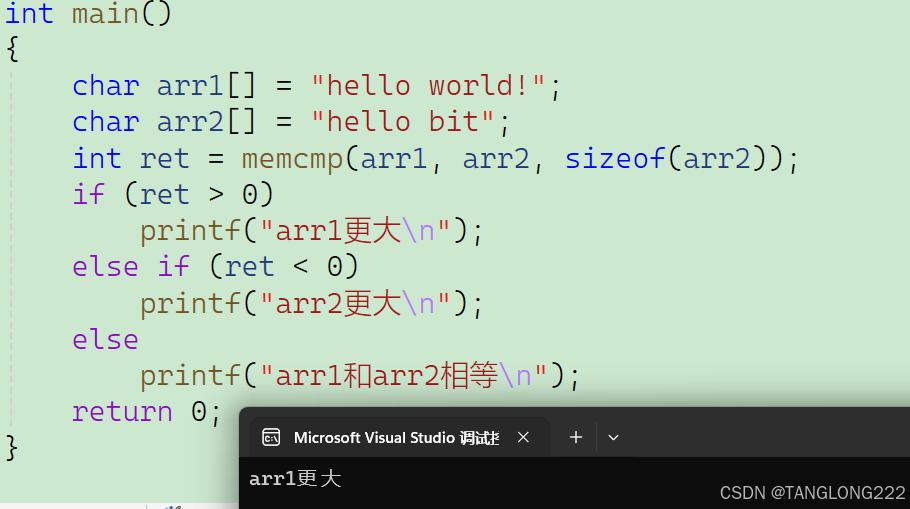
【C语言】内存函数的使用和模拟实现
文章目录 一、memcpy的使用和模拟实现二、memmove的使用和模拟实现三、memset的使用四、memcmp的使用 一、memcpy的使用和模拟实现 在之前我们学习了使用和模拟实现strncpy函数,它是一个字符串函数,用来按照给定的字节个数来拷贝字符串,那么问…...
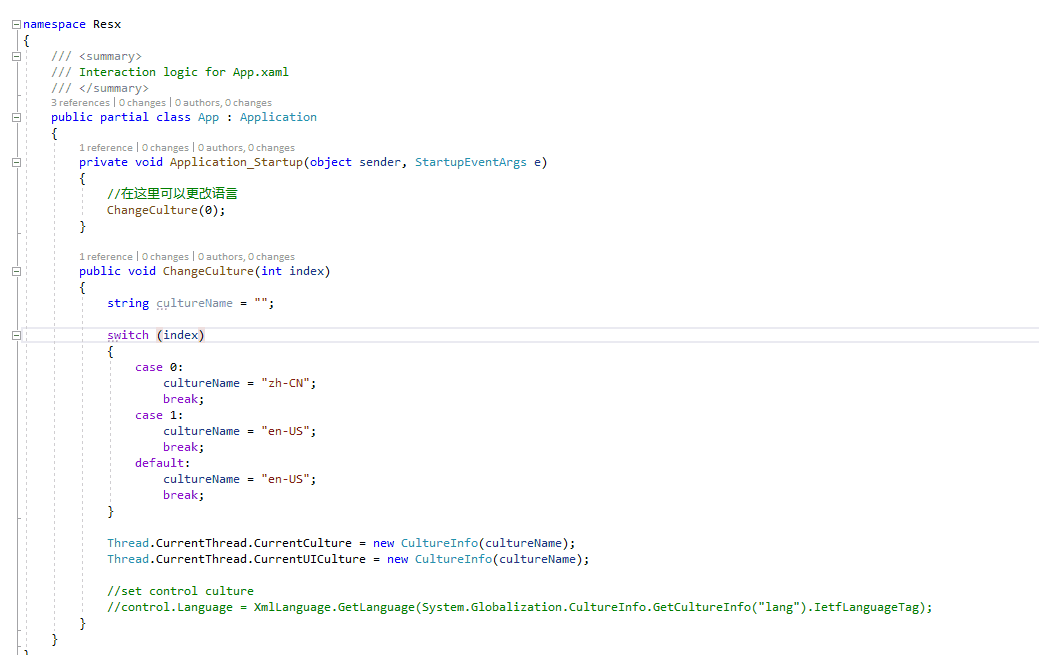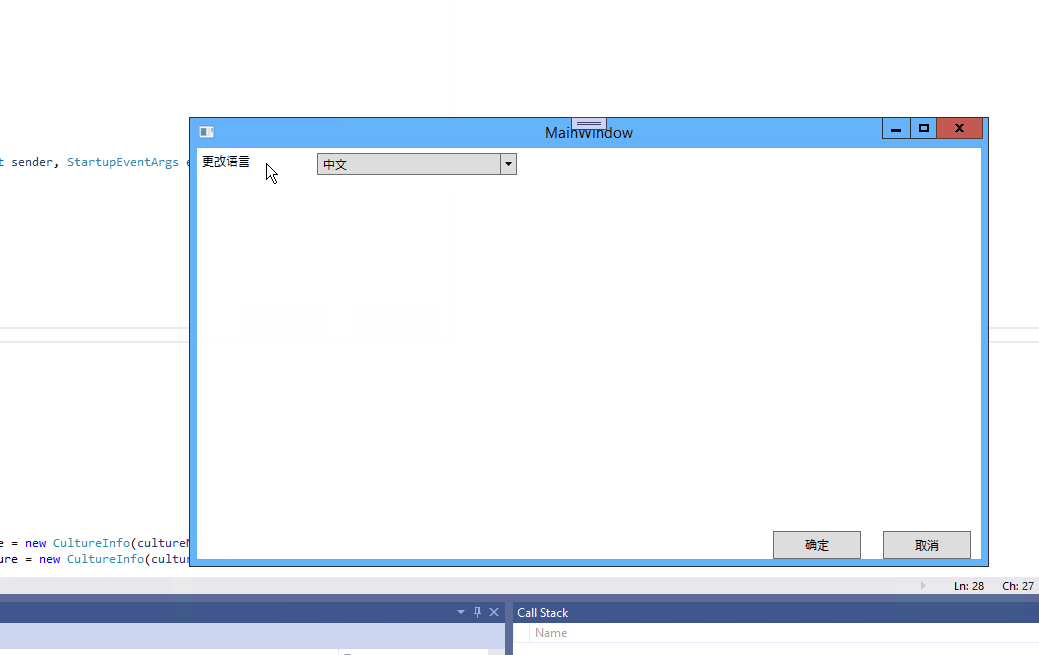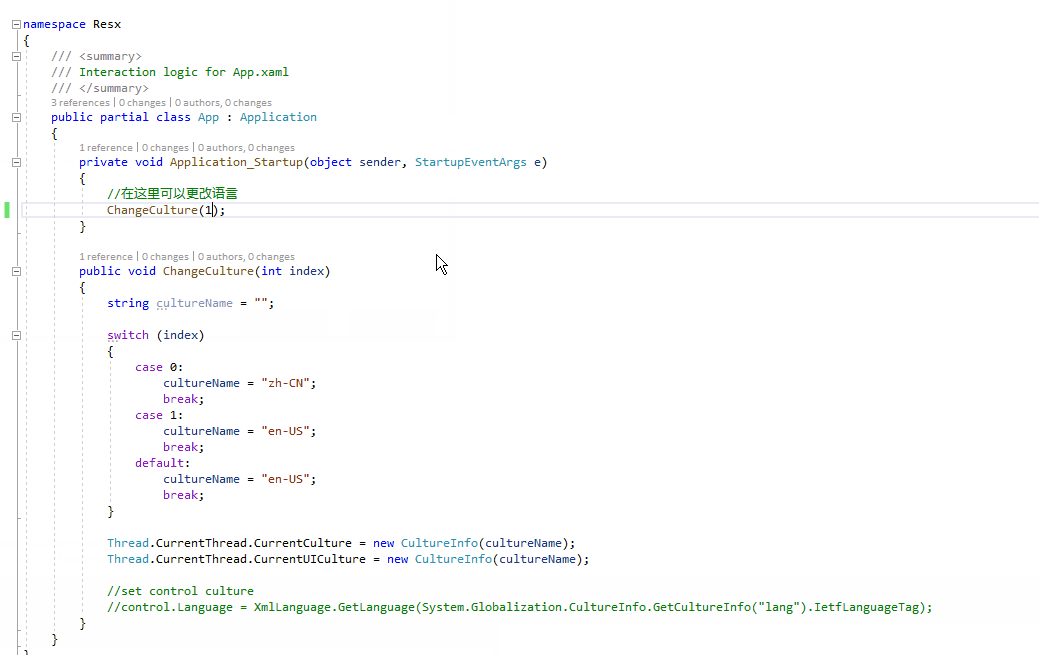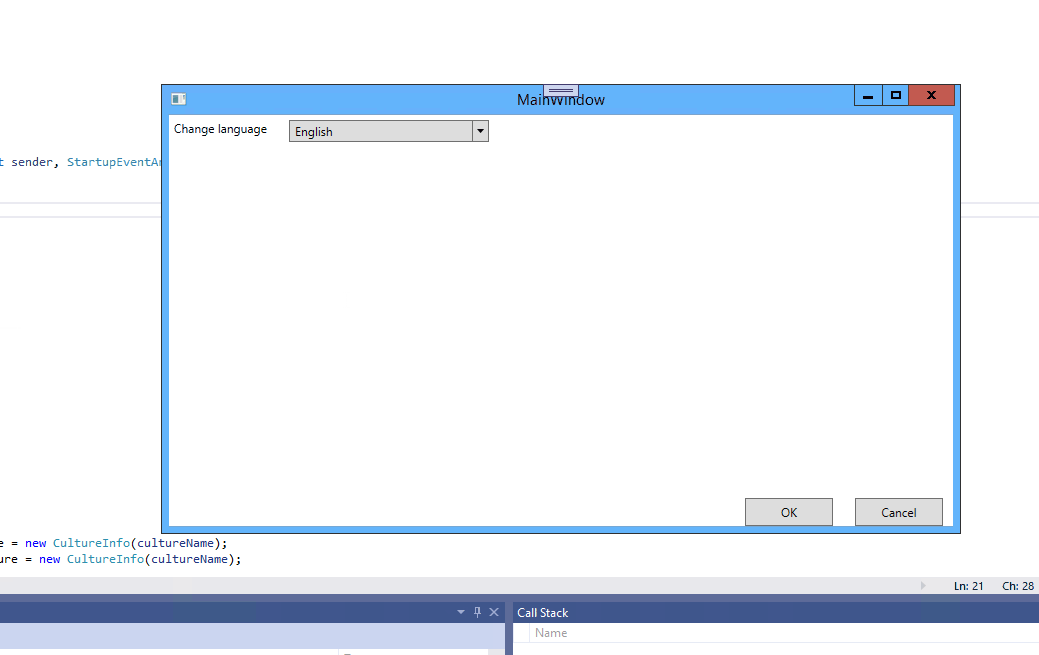
在WPF中实现多语言切换的四种方式
在WPF中有多种方式可以实现多语言,这里提供几种常用的方式。 一、使用XML实现多语言切换 使用XML实现多语言的思路就是使用XML作为绑定的数据源。主要用到XmlDataProvider类. 使用XmlDataProvider.Source属性指定XML文件的路径或通过XmlDataProvider.Document指定…...

30min 的OpenCV learning Note
1.安装python和pycharm与环境搭配 打开Windows终端:(winR)(一般使用清华镜像网站安装库比较快) pip install opencv-contrib-python -i https://pypi.mirrors.ustc.edu.cn/simple 或者 python -m pip install open…...

C--编译和链接见解
欢迎各位看官!如果您觉得这篇文章对您有帮助的话 欢迎您分享给更多人哦 感谢大家的点赞收藏评论 感谢各位看官的支持!!! 一:翻译环境和运行环境 在ANSIIC的任何一种实现中,存在两个不同的环境1,…...

【QT Quick】基础语法:基础类与控件
QML 的基础类和控件中,我们可以看到主要的几个分类:基础控件类、窗口类以及组件类。以下是对这些控件及其属性、继承关系等的详细讲解: 控件关系总结 QtObject 是所有 QML 对象的基类。它定义了基础属性,主要用于逻辑和数据封装…...

使用 SSH 连接 Docker 服务器:IntelliJ IDEA 高效配置与操作指南
使用 SSH 连接 Docker 服务器:IntelliJ IDEA 高效配置与操作指南 本文详细介绍了如何在 2375 端口未开放的情况下,通过 SSH 连接 Docker 服务器并在 Idea 中进行开发。通过修改用户权限、生成密钥对以及配置 SSH 访问,用户可以安全地远程操作…...

Gas费用是什么?
Gas费用是什么? 每5个Byte 需要1个GasGasLimit 用来限制合约最多执行多少次运算GasPrice 每次计算需要支付的费用在Web3的语境中,尤其是在以太坊(Ethereum)这样的区块链平台上,Gas费是一个核心概念。以下是关于Gas费的详细解释: 1. 定义 Gas是以太坊网络上的计算单位,…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
