信息学奥赛复赛复习11-CSP-J2020-04方格取数-动态规划、斐波那契数列、最优子结构、重叠子问题、无后效性

PDF文档回复:20241004

1 P7074 [CSP-J2020] 方格取数

[题目描述]

设有 n×m 的方格图，每个方格中都有一个整数。现有一只小熊，想从图的左上角走到右下角，每一步只能向上、向下或向右走一格，并且不能重复经过已经走过的方格，也不能走出边界。小熊会取走所有经过的方格中的整数，求它能取到的整数之和的最大值

[输入格式]

第一行有两个整数 n,m

接下来 n行每行 m 个整数，依次代表每个方格中的整数

[输出格式]

一个整数，表示小熊能取到的整数之和的最大值

[输入输出样例]

输入 #1

3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1

输出 #1

9

输入 #2

2 5
-1 -1 -3 -2 -7
-2 -1 -4 -1 -2

输出 #2

-10

说明/提示

数据规模

对于 20% 的数据，n,m≤5

对于 40% 的数据，n,m≤50

对于 70% 的数据，n,m≤300

对于 100% 的数据，1≤n,m≤10^3。方格中整数的绝对值不超过 10^4

2 相关知识点

动态规划

动态规划(Dynamic Programming) 是在20世纪50年代由美国数学家理查德-贝尔曼（Richard Bellman）发明的。

把原问题分解成若干子问题，自底向上求解最小子问题，把子问题的解存储到表格中，然后求解较大问题，求解原问题的解时，需要用到较小子问题的解，可以直接从表格中查询较小子问题的解，避免重复计算，从而提高求解效率

例题 斐波那契数列

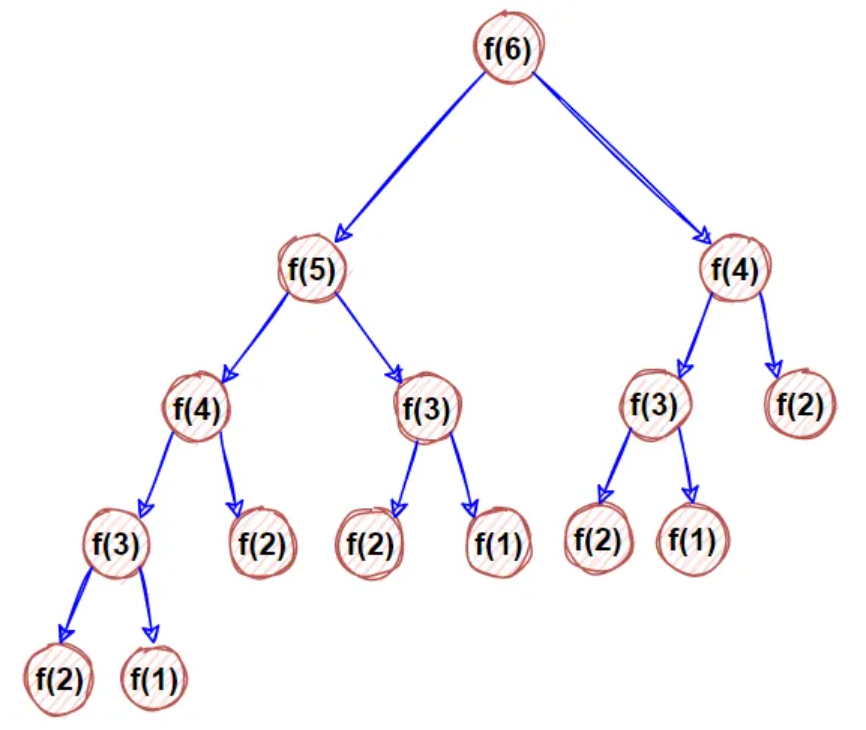
如下图

f(3)用到了3次，f(4)用到了2次，在用动态规划解决问题时，f(3)计算1次存储表格，f(4)计算1次存储表格，在使用时直接从表格取，避免重复计算，提高了速度

特别是在求较大斐波那契数时，避免了大量计算，大大提高了算法的响应时间

动态规划解决问题，一般具有如下性质

最优子结构

当一个问题的最优解包含着它的子问题的最优解时，称此问题具有最优子结构性质

也可以认为如果对每个子问题的最优解可以构建全局最优解，说明具有最优子结构

斐波那契数列例子中

f(5)=f(4)+f(3) ,f(5)的解可以通过f(4)和f(3)求出，说明具有最优子结构

如果求问题f(5)的解和子问题f(4),f(3)等子问题的解无关，则说明不具有最优子结构

重叠子问题

重叠子问题是指求解问题的过程中，每次求解的问题并不是总是新问题，有大量的重复问题存在。

斐波那契数列例子中

f(3)用到了3次，f(4)用到了2次，只计算1次，存储到数组中，后续使用时直接O(1)的时间复杂度直接取出

重叠子问题时动态规划效率高的主要原因

无后效性

把原问题分解成若干子问题，每个子问题求解都作为一个阶段，求解当前阶段解时，只与之前已经求出之前阶段的解有关，和之后未求出的阶段无关，这种称作无后效性

由于之前阶段问题的解已经求出，因此无后效性是可以使用动态规划的前提

斐波那契数列例子中

求解f(5)与f(4)和f(3)有关，不与f(5)以后的解有关，说明其具备无后效性

关键连接 -动态转移方程

动态规划解决问题时，把问题分解成一个个小问题，每个问题求解时作为一个阶段。当前阶段和下一个阶段存在着某种联系，这种确定的联系，一定存在着某种方程式(根据前一阶段通过某种关系式计算出下一阶段)，叫做动态转移方程

3 思路分析

1 可以向上、向下或向右3个方向走，因此i，j位置只会依赖上，下，左3方向
2 第1列i，j位置，只会依赖上一个方向，所以第1列所有最大累加和可以先计算
3 按列逐层推进，只需要考虑上和下2个方向
示例数据
3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1
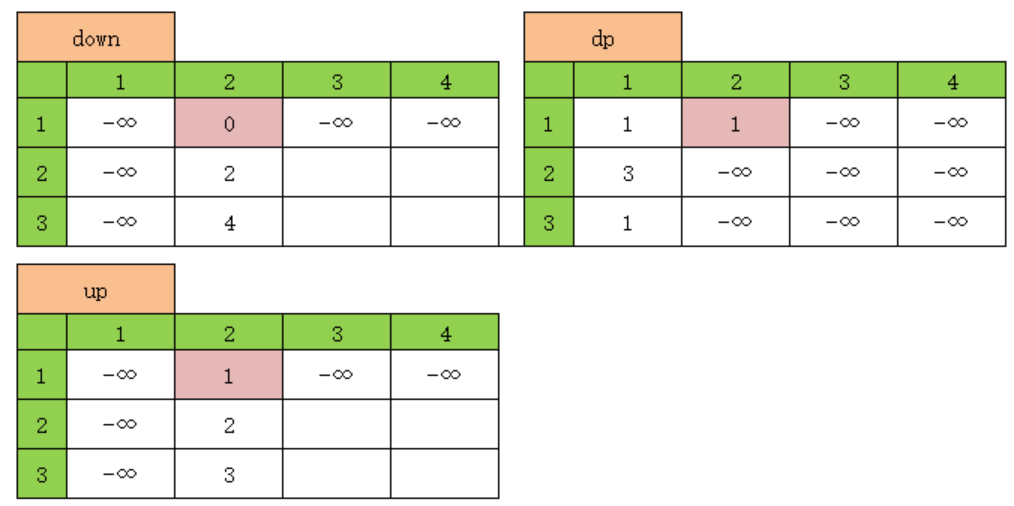
dp[i][j]表示从1,1走到i,j的最大累加和
可以通过down和up数组取最大值获得，max(down[i][j],up[i][j])
例如dp[1][2]=max(down[1][2],up[1][2])
具体如下图红色单元格

示例程序

#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int N=1e3+10;//表格长宽最大值 
int ipt[N][N];//输入到方格的数
/*
down[i][j] i列从长到下的累加到j最大和
up[i][j] i从下到上的累加到j最大和
dp[i][j] 从1,1开始累加到i,j的最大和
*/ 
LL down[N][N],up[N][N],dp[N][N];
int n,m;//n行 m列 int main(){scanf("%d%d",&n,&m);//输入n行 m列 for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%lld",&ipt[i][j]);//输入n行m列个数 }}//对 down,up,dp数组初始值，默认负数最小值，小于-10^4	memset(down,128,sizeof(down));memset(up,128,sizeof(up));memset(dp,128,sizeof(dp));dp[1][1]=ipt[1][1];//dp[1][1] 为ipt[1][1] for(int i=2;i<=n;i++){//累加第1列 赋初始值 dp[i][1]=dp[i-1][1]+ipt[i][1];//第1列只能从上到下 }for(int j=2;j<=m;j++){//计算第2~m列 dp数组的值//计算j列时，j-1列已经计算好 for(int i=1;i<=n;i++){//从上到下计算j列的最大累加和 down[i][j]=max(down[i-1][j],dp[i][j-1])+ipt[i][j];}for(int i=n;i>=1;i--){//从下到上计算j列的最大累加和 up[i][j]=max(up[i+1][j],dp[i][j-1])+ipt[i][j];}/*到i,j位置可能有3个方向(i,j-1),(i-1,j),(i+1,j) (i-1,j)对应down[i][j], (i+1,j)对应up[i][j]其中计算down和up时，都和 (i,j-1)做个比较取最大后+ ipt[i][j]所以down和up都大于 (i,j-1)因此值需要在down[i][j]和up[i][j]取最大即可 */ for(int i=1;i<=n;i++){ dp[i][j]=max(down[i][j],up[i][j]);}}cout<<dp[n][m];//输出从左上角走到n,m的最大值 return 0;
}