算法训练营打卡Day19
目录
1.二叉搜索树的最近公共祖先
2.二叉树中的插入操作
3.删除二叉搜索树中的节点
题目1、二叉搜索树的最近公共祖先
力扣题目链接(opens new window)
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
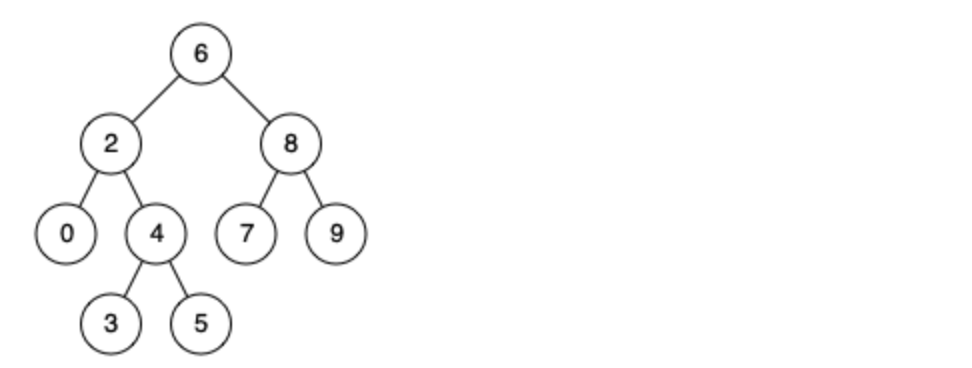
示例 1:
- 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
- 输出: 6
- 解释: 节点 2 和节点 8 的最近公共祖先是 6。
思路
我们从二叉搜索树的根节点开始遍历,通过判断传入的两个参数节点的值,与根节点的值的大小关系,然后判断从根节点的左子树还是右子树开始搜索,如果遍历到叶子结点时还没有搜索到参数节点的值,我们就可以返回NULL;我们可以使用递归的思路求解, 最终的返回值是对应的root。
代码实现
CPP
执行逻辑主要包括三种:p、q的值都比当前节点值大;p、q的值都比当前节点值小;p、q在当前节点的一左一右
class Solution {
private:TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) {if (cur == NULL) return cur;// 中if (cur->val > p->val && cur->val > q->val) { // 左TreeNode* left = traversal(cur->left, p, q);if (left != NULL) {return left;}}if (cur->val < p->val && cur->val < q->val) { // 右TreeNode* right = traversal(cur->right, p, q);if (right != NULL) {return right;}}return cur;}
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {return traversal(root, p, q);}
};Python
class Solution:def lowestCommonAncestor(self, root, p, q):if root.val > p.val and root.val > q.val:return self.lowestCommonAncestor(root.left, p, q)elif root.val < p.val and root.val < q.val:return self.lowestCommonAncestor(root.right, p, q)else:return root题目2、二叉树中的插入操作
力扣题目链接(opens new window)
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

思路
对于二叉搜索树中的插入操作,我能不能把二叉搜索树先转换成有序数组,再把给定的整数插入转换后的有序数组,最后进行中序遍历来得到新的二叉搜索树?
理论上可行,但是显然不是最优解。
-
时间复杂度:
- 转换BST为有序数组:这个操作需要中序遍历BST,时间复杂度为O(n),其中n是BST的节点数。
- 在有序数组中插入元素:在有序数组中插入一个元素需要找到正确的位置,并可能移动其他元素,时间复杂度为O(n)。
- 从有序数组重建BST:将有序数组转换为BST的过程(例如,使用递归的方式构建平衡BST)通常也有O(n)的时间复杂度。
综合起来,这个方法的总时间复杂度为O(n) + O(n) + O(n) = O(3n),即O(n)。虽然从表面上看这个时间复杂度与直接在BST中插入的时间复杂度O(log n)(在平衡BST中)或O(n)(在最坏情况下,如退化为链表)相比没有显著区别,但实际操作中会有额外的空间开销和步骤,且可能破坏BST的平衡性。
我们可以不考虑题目中提示所说的改变树的结构的插入方式,只要按照二叉搜索树的规则去遍历,遇到空节点就插入节点就可以了。
代码实现
CPP
假如遇到空节点,我们直接插入并返回该节点;假如当前节点的值大于要插入的值,我们在左子树进行插入操作,否则在右子树操作。我们可以使用递归的思路。
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}if (root->val > val) root->left = insertIntoBST(root->left, val);if (root->val < val) root->right = insertIntoBST(root->right, val);return root;}
};python
class Solution:def insertIntoBST(self, root, val):if root is None:node = TreeNode(val)return nodeif root.val > val:root.left = self.insertIntoBST(root.left, val)if root.val < val:root.right = self.insertIntoBST(root.right, val)return root题目3、删除二叉搜索树中的节点
力扣题目链接(opens new window)
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点; 如果找到了,删除它。 说明: 要求算法时间复杂度为 $O(h)$,h 为树的高度。
示例:

思路
首先我们自然地回去想找到需要删除的节点,如果找到目标节点,我们就删除它。但是我们要考虑节点是叶子结点、只拥有左子树/右子树的节点、根节点的情况,听上去会比较复杂。
分类讨论:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
代码实现
CPP
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了if (root->val == key) {// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点if (root->left == nullptr && root->right == nullptr) {///! 内存释放delete root;return nullptr;}// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点else if (root->left == nullptr) {auto retNode = root->right;///! 内存释放delete root;return retNode;}// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点else if (root->right == nullptr) {auto retNode = root->left;///! 内存释放delete root;return retNode;}// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置TreeNode* tmp = root; // 把root节点保存一下,下面来删除root = root->right; // 返回旧root的右孩子作为新rootdelete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};python
class Solution:def deleteNode(self, root, key):if root is None: # 如果根节点为空,直接返回return rootif root.val == key: # 找到要删除的节点if root.right is None: # 如果右子树为空,直接返回左子树作为新的根节点return root.leftcur = root.rightwhile cur.left: # 找到右子树中的最左节点cur = cur.leftroot.val, cur.val = cur.val, root.val # 将要删除的节点值与最左节点值交换root.left = self.deleteNode(root.left, key) # 在左子树中递归删除目标节点root.right = self.deleteNode(root.right, key) # 在右子树中递归删除目标节点return root#如果二叉搜索树改成普通二叉树,思路和代码实现又会变得不同
相关文章:

算法训练营打卡Day19
目录 1.二叉搜索树的最近公共祖先 2.二叉树中的插入操作 3.删除二叉搜索树中的节点 题目1、二叉搜索树的最近公共祖先 力扣题目链接(opens new window) 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有…...

H.264编解码工具 - FFmpeg
一、简介 FFmpeg是一款用于处理多媒体数据的开源软件,可以完成音频、视频和多媒体流的编解码、转码、解码、录制、流媒体播放等功能。它提供了丰富的命令行工具和库函数,适用于各种平台和操作系统。 FFmpeg支持多种常见的音视频格式,包括MP3、WAV、FLAC、MP4、AVI、MKV等。它…...

60 序列到序列学习(seq2seq)_by《李沐:动手学深度学习v2》pytorch版
系列文章目录 文章目录 系列文章目录一、理论知识比喻机器翻译Seq2seq编码器-解码器细节训练衡量生成序列的好坏的BLEU(值越大越好)总结 二、代码编码器解码器损失函数训练预测预测序列的评估小结练习 一、理论知识 比喻 seq2seq就像RNN的转录工作一样,非常形象的比…...

elementPlus的tree组件点击后有白色背景
在使用elementPlus的tree组件时,需要对它进行样式的重写,下面是相关代码 <script setup> import { ref } from vue const data [{label: Level one 1,children: [{label: Level two 1-1,children: [{label: Level three 1-1-1}]}]},{label: Leve…...

【Git】Git在Unity中使用时的问题记录
个人向笔记。 (为什么没截图,因为公司电脑没法截图!) 1 前言 主要记录在使用Git协同开发时的各种问题,方便以后查阅。 2 记录 2.1 合并冲突 git pull下来后直接给合并了,麻了。若不想直接合并应该先把分…...

python学习记录6
(1)循环嵌套 可以将一个循环语句所属的语句块也可以是一个完整的一个循环语句,一般嵌套不应该超过3层。 嵌套可以是while-while、for-for,也可以是while-for。 基本图形输出:正方形,直角三角形 #输入一个数字n&…...

MongoDB 的基本使用
目录 数据库的创建和删除 创建数据库 查看数据库 删除数据库 集合的创建和删除 显示创建 查看 删除集合 隐式创建 文档的插入和查询 单个文档的插入 insertOne insertMany 查询 嵌入式文档 查询数组 查询数组元素 为数组元素指定多个条件 通过对数组元素使…...

数据揭秘:分类与预测技术在商业洞察中的应用与实践
分类与预测:数据挖掘中的关键任务 在数据挖掘的广阔天地中,分类与预测就像是一对互补的探险家,它们携手深入数据的丛 林,揭示隐藏的宝藏。 一、分类:数据的归类大师 分类是一种将数据点按照特定的属性或特征划分到不…...

学MybatisPlus
1.设置MySql的数据库 spring:datasource:url: jdbc:mysql://127.0.0.1:3306/mp?useUnicodetrue&characterEncodingUTF-8&autoReconnecttrue&serverTimezoneAsia/Shanghaidriver-class-name: com.mysql.cj.jdbc.Driverusername: rootpassword: MySQL123 logging:l…...
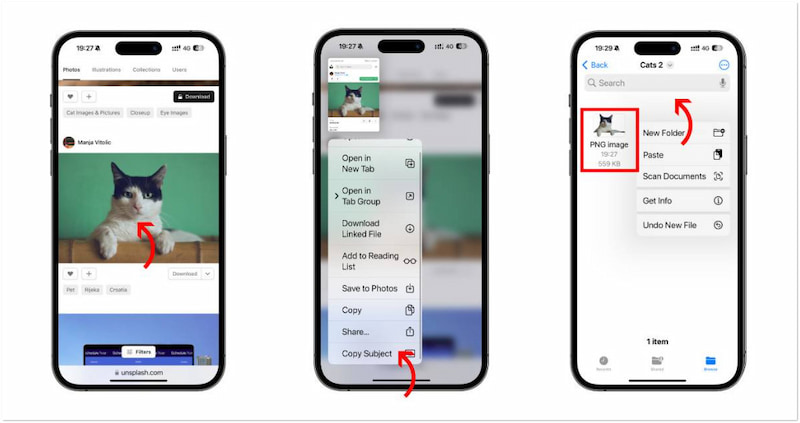
如何使用工具删除 iPhone 上的图片背景
在 iPhone 上删除背景图像变得简单易行。感谢最近 iOS 更新中引入的新功能。如今,iOS 用户现在可以毫不费力地删除背景,而无需复杂的应用程序。在这篇文章中,您将学习如何使用各种方法去除 iPhone 上的背景。这可确保您可以选择最适合您偏好的…...
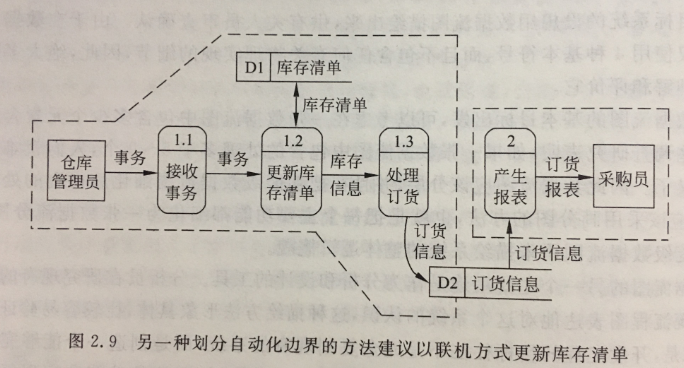
软件工程-数据流图
数据流图(Data Flow Diagram,DFD)是一种图形化技术,它描绘信息流和数据从输入移动到输出的过程中所经受的变换。 数据流图的设计原则 数据守恒原则,对于任何一个加工来说,其所有输出数据流中的数据必须能从该加工的输入数据流中…...

链式前向星(最通俗易懂的讲解)
链式前向新:用于存储图的 边集 数组 前言 当我们存储图的时候,往往会使用 邻接矩阵 或是 邻接表。 邻接矩阵 好写,但太浪费空间,节点一多就存不下; 邻接表 效率高,但涉及指 ,不好写容易出错…...
创建型模式:简单工厂模式,工厂方法模式,抽象工厂模式)
【C++设计模式】(四)创建型模式:简单工厂模式,工厂方法模式,抽象工厂模式
文章目录 (四)创建型模式:简单工厂模式,工厂方法模式,抽象工厂模式简单工厂模式工厂方法模式抽象工厂模式 (四)创建型模式:简单工厂模式,工厂方法模式,抽象工…...
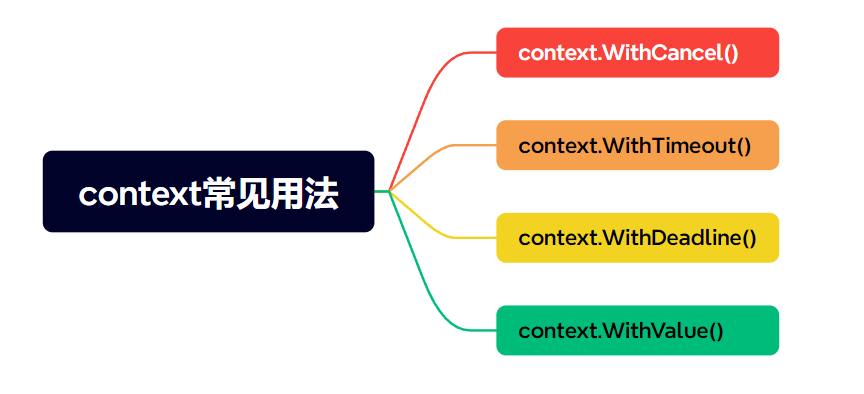
浅析Golang的Context
文章目录 1. 简介2. 常见用法2.1 控制goroutine的生命周期(cancel)2.2 传递超时(Timeout)信息2.3 传递截止时间(Deadline)2.4 传递请求范围内的全局数据 (value) 3 特点3.1 上下文的…...

生日礼物C++代码
#include<bits/stdc.h> using namespace std; string s; int a,b; int main(){cout<<" 生日之地"<<\n;cout<<" 1.开始游戏"<<" 2.不想开始"<<\n;cin>>a;if(a1||a2){if(a2)cout<<…...

使用python基于DeepLabv3实现对图片进行语义分割
DeepLabv3 介绍 DeepLabv3 是一种先进的语义分割模型,由 Google Research 团队提出。它在 DeepLab 系列模型的基础上进行了改进,旨在提高图像中像素级分类的准确性。以下是 DeepLabv3 的详细介绍: 概述DeepLabv3 是 DeepLab 系列中的第三代…...

【漏洞复现】泛微OA E-Office do_excel.php 任意文件写入漏洞
》》》产品描述《《《 泛微0-0fice是一款标准化的协同 OA办公软件,泛微协同办公产品系列成员之一,实行通用化产品设计,充分贴合企业管理需求,本着简洁易用、高效智能的原则,为企业快速打造移动化、无纸化、数字化的办公平台。 》》…...
)
算法(食物链)
240. 食物链 题目 动物王国中有三类动物 A,B,C𝐴,𝐵,𝐶,这三类动物的食物链构成了有趣的环形。 A𝐴 吃 B𝐵,B𝐵 吃 C𝐶,C𝐶 吃 A𝐴。…...

ubuntu20.04系统安装zookeeper简单教程
Ubuntu系统中安装和配置Zookeeper的完整指南 Apache Zookeeper是一个开源的分布式协调服务,广泛用于分布式应用程序中管理配置、提供命名服务、分布式同步以及组服务等。在本教程中,我们将详细介绍如何在Ubuntu系统中安装Zookeeper,并进行相关…...

.NET Core 高性能并发编程
一、高性能大并发架构设计 .NET Core 是一个高性能、可扩展的开发框架,可以用于构建各种类型的应用程序,包括高性能大并发应用程序。为了设计和开发高性能大并发 .NET Core 应用程序,需要考虑以下几个方面: 1. 异步编程 异步编程…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
