动态规划(Dynamic Programming)——背包问题
动态规划(Dynamic Programming)
背包问题
目录
- 动态规划(Dynamic Programming)
- 背包问题
- 01背包问题
- 输入格式
- 输出格式
- 数据范围
- 输入样例
- 输出样例:
- 二维
- 一维
- 完全背包问题
- 多重背包问题
- 输入格式
- 输出格式
- 数据范围
- 输入样例
- 输出样例:
- 数据范围
- 二进制优化
- 分组背包问题
- 输入格式
- 输出格式
- 数据范围
- 输入样例
- 输出样例:
01背包问题
动态规划
- 状态表示
f[i][j]- 集合:所有考虑前i个物品,且体积不大于j的全部选法
- 属性:Max
- 状态计算:集合的划分
有 N件物品和一个容量是 V的背包。每件物品只能使用一次。
第 i 件物品的体积是 viv_ivi,价值是wiw_iwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wiv_i,w_ivi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤1000
0<vi,wi≤10000< vi,wiv_i,w_ivi,wi≤1000输入样例
4 5 1 2 2 4 3 4 4 5输出样例:
8
二维
-
状态f[i][j]定义:前 i个物品,背包容量 j下的最优解(最大价值)
-
当背包容量够,需要决策选与不选第 i 个物品:
- 不选
f[i][j] = f[i-1][j] - 选
f[i][j]=f[i-1][j-v[i]]+w[i] - 我们的决策是如何取到最大价值,因此以上两种情况取
max()
代码
#include <iostream> #include <algorithm> using namespace std; const int N = 1010; int v[N], w[N]; int f[N][N]; int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i)cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {f[i][j] = f[i - 1][j];if (v[i] <= j) f[i][j] = max(f[i][j], f[i -1][j - v[i]] + w[i]);}}cout << f[n][m];return 0; } - 不选
一维
我们定义的状态f[i][j]可以求得任意合法的i与j最优解,但题目只需要求得最终状态f[n][m],因此我们只需要一维的空间来更新状态。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int v[N], w[N];
int f[N];
int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i)cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i) {for (int j = m; j >= v[i]; --j) {f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m];return 0;
}
完全背包问题
动态规划
- 状态表示
f[i][j]- 集合:所有考虑前i个物品,且体积不大于j的全部选法
- 属性:Max
- 状态计算:集合的划分
f[i][j]第i个物品选了k个,先去掉k个物品i,再加回来k个物品i
f[i][j] = f[i-1][j-v[i]*k]+w[i]*k
暴力dp
#include <iostream>using namespace std;
const int N = 1010;
int f[N][N],v[N], w[N];
int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {for (int k = 0; k * v[i] <= j; ++k) {f[i][j] = max(f[i][j],f[i - 1][j - k * v[i]] + k * w[i]);// cout << f[i][j];}}}cout << f[n][m];return 0;
}
我们可以发现
f[i,j]=Max(f[i-1,j],f[i-1,j-v]+w,f[i-1.j-2v]+2w,...,f[i-1.j-kv]+kw
f[i,j-v]=Max( f[i-1,j-v],f[i-1.j-2v]+w,...,f[i-1.j-kv]+(k-1)w
代码
#include <iostream>
// #include <algorithm>
using namespace std;
const int N = 1010;
int f[N][N],v[N], w[N];
int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {f[i][j] = f[i-1][j];if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j-v[i]] + w[i]); }}cout << f[n][m];return 0;
}
一维代码
#include <iostream>
// #include <algorithm>
using namespace std;
const int N = 1010;
int f[N],v[N], w[N];
int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];for (int i = 1; i <= n; ++i) {for (int j = v[i]; j <= m; ++j) {// f[i][j] = f[i-1][j];f[j] = max(f[j], f[j-v[i]] + w[i]); }}cout << f[m];return 0;
}
多重背包问题
动态规划
- 状态表示
f[i][j]- 集合:所有考虑前i个物品,且体积不大于j的全部选法
- 属性:Max
- 状态计算:集合的划分
题目描述
有 N 种物品和一个容量是 V 的背包。
第 i种物品最多有 sis_isi 件,每件体积是 viv_ivi ,价值是 wiw_iwi 。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 viv_ivi, wiw_iwi, sis_isi ,用空格隔开,分别表示第 i种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<viv_ivi, wiw_iwi, sis_isi ≤100输入样例
4 5 1 2 3 2 4 1 3 4 3 4 5 2输出样例:
10
代码
#include <iostream>
using namespace std;
const int N = 110;
int f[N][N], w[N], v[N], s[N];
int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i] >> s[i];for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j) {for (int k = 0; k * v[i] <= j && k <= s[i]; ++k) {f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);}}cout << f[n][m];return 0;
}
当数据范围扩大
数据范围
0<N≤1000
0<V≤2000
0<viv_ivi, wiw_iwi, sis_isi ≤2000
f(i, j) = Max(f(i-1,j),f(i-1,j-v)+w,f(i-1,j-2v)+2w+...+f(i-1,j-sv)+sw)
f(i, j-v) = Max(f(i-1,j-v),f(i-1,j-2v)+w,f(i-1,j-3v)+2w+...+f(i-1,j-sv)+(s-1)w,f(i, j) = Max(f(i-1,j),f(i-1,j-v)+w,f(i-1,j-2v)+2w+...+f(i-1,j-(s+1)v)+sw)
所以不能用完全背包问题解决
我们可以采用二进制优化+01背包问题的方法
二进制优化
给出一堆苹果和10个箱子,选出n个苹果。将这一堆苹果分别按照1,2,4,8,16,…512分到10个箱子里,那么由于任何一个数字x∈[0,1023] (第11个箱子才能取到1024,评论区有讨论这个)都可以从这10个箱子里的苹果数量表示出来,但是这样选择的次数就是 ≤10次
代码
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int v[N], w[N];
int f[2020];
int main() {int n, m;cin >> n >> m;int cnt = 0;while (n--) {int a, b, s;cin >> a >> b >> s;int k = 1;while (k <= s) {v[++cnt] = a * k;w[cnt] = b * k;s -= k;k *= 2;}if (s){v[++cnt] = a * s;w[cnt] = b * s;}}n = cnt;for (int i = 1; i <=n; ++i) {for (int j = m; j >= v[i]; --j) {f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m];return 0;
}
分组背包问题
有 N 组物品和一个容量是 V的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是vi,jv_{i,j}vi,j,价值是wi,jw_{i,j}wi,j,其中 i 是组号,j 是组内编号。求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
- 每组数据第一行有一个整数 SiS_{i}Si,表示第 i 个物品组的物品数量;
- 每组数据接下来有 SiS_{i}Si 行,每行有两个整数vi,jv_{i,j}vi,j,wi,jw_{i,j}wi,j,用空格隔开,分别表示第 i个物品组的第 j 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<Si≤100
0<vi,jv_{i,j}vi,j,wi,jw_{i,j}wi,jj≤100输入样例
3 5 2 1 2 2 4 1 3 4 1 4 5输出样例:
8
代码
#include <iostream>
using namespace std;
const int N = 110;
int v[N], w[N];
int f[110];
int main() {int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i) {int s;cin >> s;for (int j = 1; j <= s; ++j) {cin >> v[j] >> w[j];}for (int k = m; k >= 1; --k) {for (int j = 1; j <= s; ++j) {if (v[j] <= k)f[k] = max(f[k], f[k - v[j]] + w[j]);}} }cout << f[m];return 0;
}
相关文章:
——背包问题)
动态规划(Dynamic Programming)——背包问题
动态规划(Dynamic Programming) 背包问题 目录动态规划(Dynamic Programming)背包问题01背包问题输入格式输出格式数据范围输入样例输出样例:二维一维完全背包问题多重背包问题输入格式输出格式数据范围输入样例输出样例:数据范围二进制优化分组背包问题…...

JVM学习02:内存结构
JVM学习02:内存结构 1. 程序计数器 1.1、定义 Program Counter Register 程序计数器(寄存器) 作用:是记住下一条jvm指令的执行地址 特点: 是线程私有的不会存在内存溢出 1.2、作用 程序计数器物理上是由寄存器来实…...
6年软件测试经验,从我自己的角度理解自动化测试
接触了不少同行,由于他们之前一直做手工测试,现在很迫切希望做自动化测试,其中不乏工作5年以上的人。 本人从事软件自动化测试已经近6年,从server端到web端,从API到mobile,切身体会到自动化带来的好处与痛楚…...

三种方式查看linux终端terminal是否可以访问外网ping,curl,wget
方法1:ping注意不要用ping www.google.com.hk来验证,因为有墙,墙阻止了你接受网址发回的响应数据。即使你那啥过,浏览器都可以访问Google,terminal里面也是无法得到响应 百度在墙内,所以可以正常拿到响应信…...

【Call for papers】SIGCOMM-2023(CCF-A/计算机网络/2023年2月15日截稿)
ACM SIGCOMM is the flagship annual conference of the ACM Special Interest Group on Data Communication (SIGCOMM). ACM SIGCOMM 2023, the 37th edition of the conference series, will be held in New York City, US, September 10 - 14, 2023. 文章目录1.会议信息2.时…...

Chapter5:机器人感知
ROS1{\rm ROS1}ROS1的基础及应用,基于古月的课,各位可以去看,基于hawkbot{\rm hawkbot}hawkbot机器人进行实际操作。 ROS{\rm ROS}ROS版本:ROS1{\rm ROS1}ROS1的Melodic{\rm Melodic}Melodic;实际机器人:Ha…...
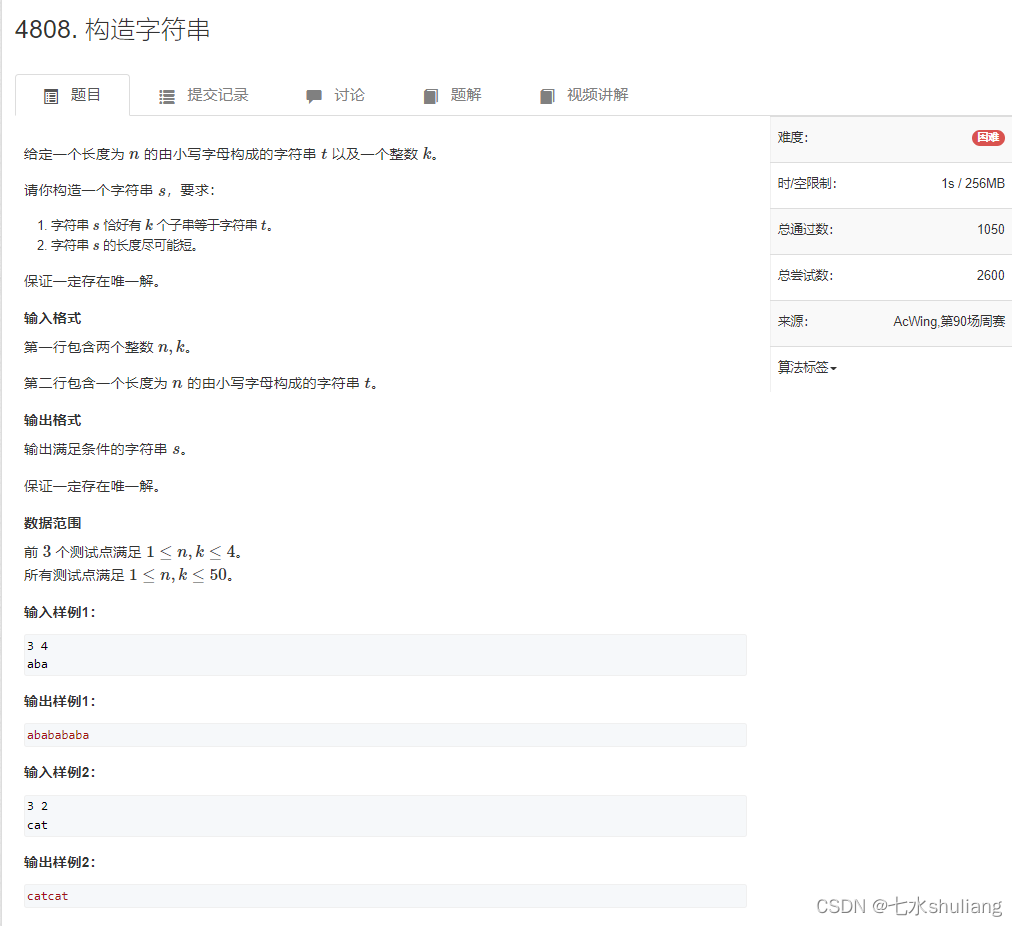
[acwing周赛复盘] 第 90 场周赛20230211 补
[acwing周赛复盘] 第 90 场周赛20230211 补 一、本周周赛总结二、 4806. 首字母大写1. 题目描述2. 思路分析3. 代码实现三、4807. 找数字1. 题目描述2. 思路分析3. 代码实现四、4808. 构造字符串1. 题目描述2. 思路分析3. 代码实现六、参考链接一、本周周赛总结 T1 模拟T2 模拟…...

数组
一、数组中重复的数字题目描述:在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1…...
:AXI_UARTLITE的使用)
MicroBlaze系列教程(4):AXI_UARTLITE的使用
文章目录 @[toc]AXI_UARTLITE简介MicroBlaze添加串口IP常用函数使用示例参考资料工程下载本文是Xilinx MicroBlaze系列教程的第4篇文章。 AXI_UARTLITE简介 axi_uartlite是Xilinx提供axi-lite接口的通用串口IP核,用AXI-Lite总线接口和用户进行交互,速度可以根据不同的芯片调…...
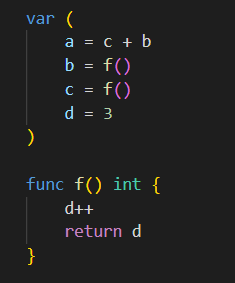
GO 中的 init 函数
前言 go 语言中有一个非常神奇的函数 init ,它可以在所有程序执行开始前被执行,并且每个 package 下面可以存在多个 init 函数,我们一起来看看这个奇怪的 init 函数。 init 特性 init 函数在 main 函数之前执行,并且是自动执行;…...
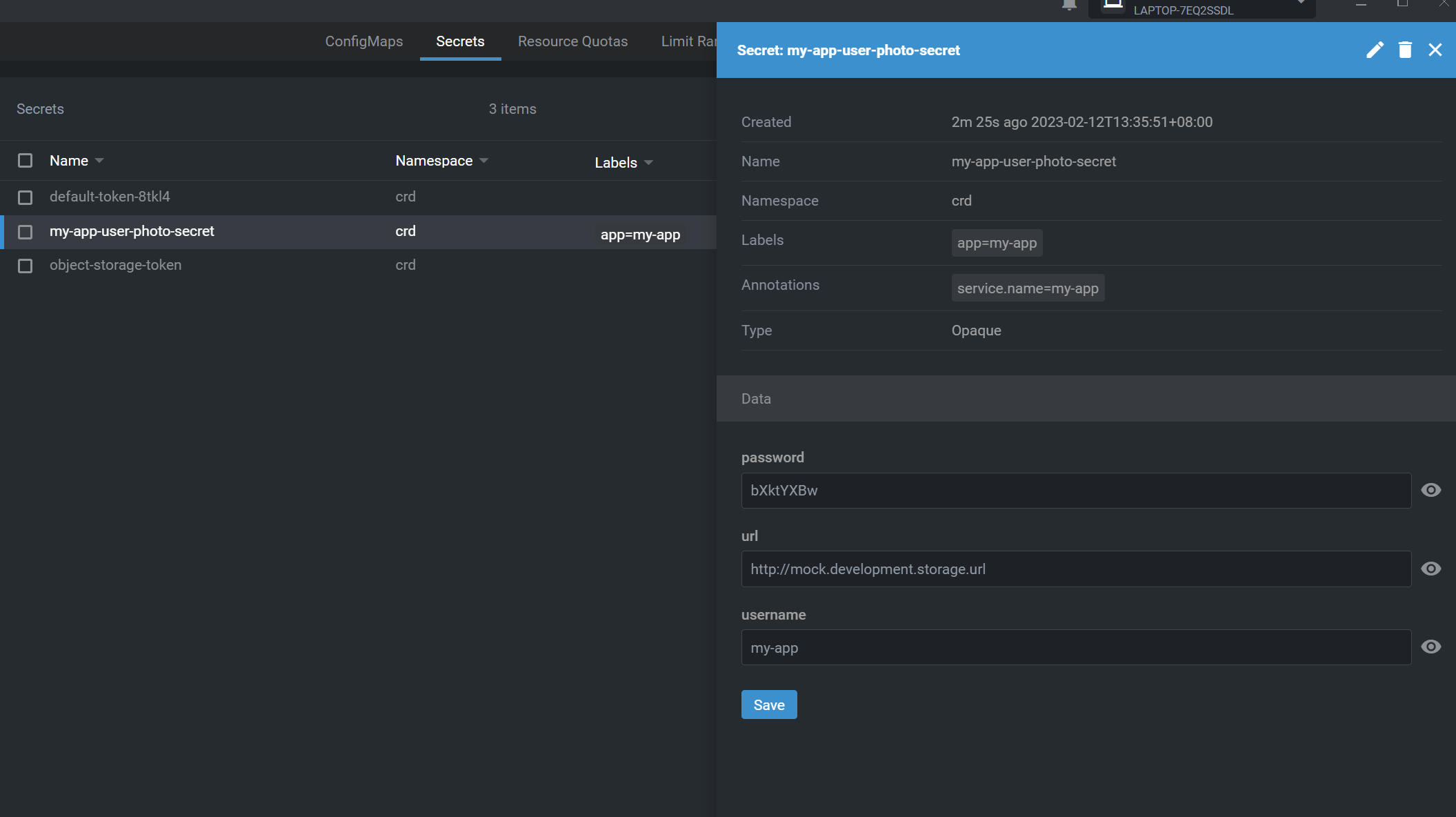
使用C#编写k8s CRD Controller
本文项目地址:k8s-crd - Repos (azure.com)CRDCRD指的是Custom Resource Definition。开发者更多的关注k8s对于容器的编排与调度,这也是k8s最初惊艳开发者的地方。而k8s最具价值的地方是它提供了一套标准化、跨厂商的 API、结构和语义。k8s将它拥有的一切…...

Ansible---playbook剧本
目录 引言:什么是playbook? 一、Playbook 1.1、playbook中的核心元素 1.2、playbook中的基础组件 1.3、playbook格式说明 1.4、实例:httpd服务剧本 二、playbook中的模块 2.1、Templates 模块 2.2、tags 模块 2.3、Roles 模块 引言&…...
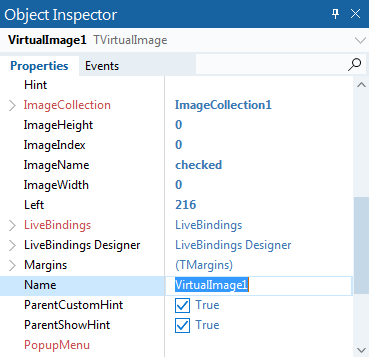
Delphi 中TImageCollection和TVirtualImageList 控件实现high-DPI
一、概述RAD Studio允许你通过使用TImageCollection组件和TVirtualImageList组件,在你的Windows VCL应用程序中包含缩放、高DPI、多分辨率的图像。这两个组件位于Windows 10面板中:注意:如果你使用FireMonkey进行跨平台应用,请看T…...

Ros中如何给UR5配置自定义工具 | 在Rviz中给UR5机器人装载定义工具 | UR5配置自定义末端执行器
前言 在学习和项目研究的过程中,我需要在Ur5e上装上工具,以对现实场景进行仿真。网上会有一些装载/配置现成的夹爪,例如Robotiq等。但和我们装载自定义工具的场景还有些差异,因此写一篇博客记录,可能有偏差。如果有问…...
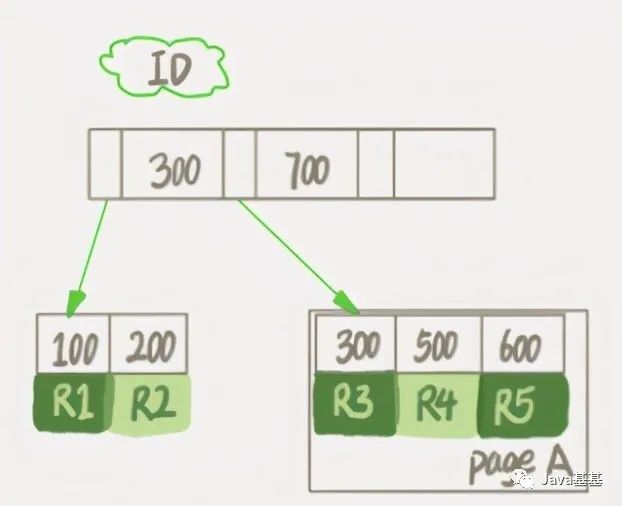
数据库 delete 表数据后,磁盘空间为什么还是被一直占用?
插: 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 坚持不懈,越努力越幸运,大家一起学习鸭~~~ 最近有个上位机获取下位机上报数据的项目,…...
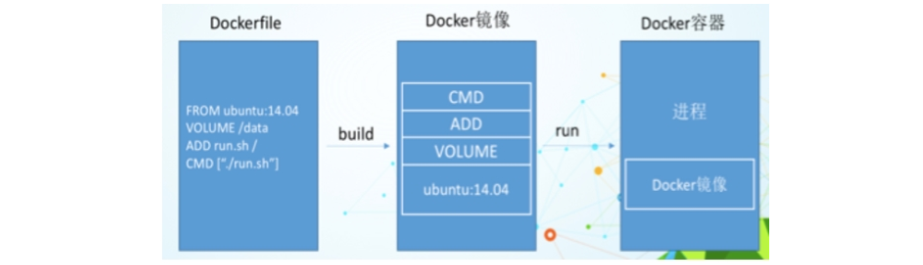
docker-微服务篇
docker学习笔记1.docker简介1.1为什么会出现docker?1.2docker理念1.3虚拟机(virtual machine)1.4容器虚拟化技术1.5一次构建到处运行2.docker安装2.1前提条件2.2docker基本构成2.3docker安装步骤*2.4测试镜像3.docker常用命令3.1 启动docker3…...
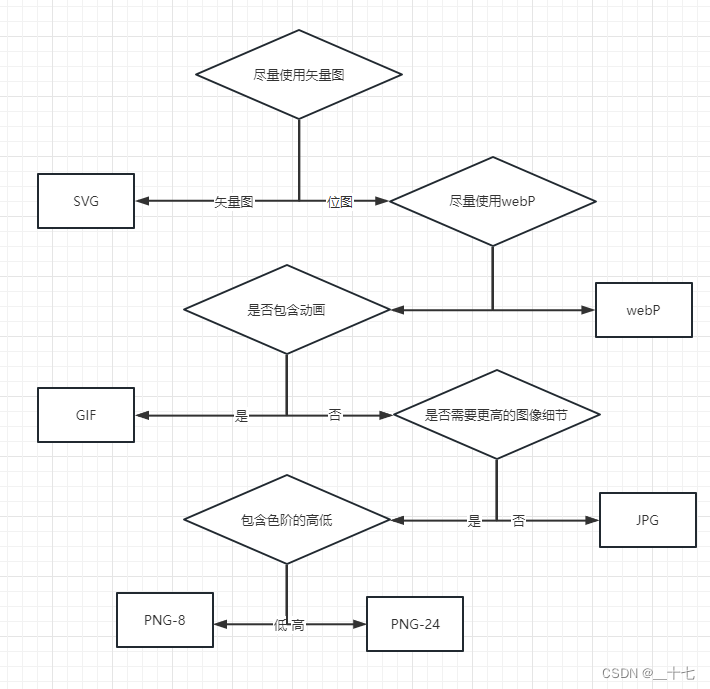
图像优化篇
目录(1)矢量图(2)位图 2.1 分辨率2,图像格式格式选择建议:(1)矢量图 被定义为一个对象,包括颜色,大小,形状,以及屏幕位置等属性&…...

在surface go 2上安装ubuntu 20.04
在surface go 2上安装ubuntu 20.04 1.制作安装盘 下载ubuntu系统的iso文件 使用Rufus软件将u盘制作为ubuntu系统的安装盘 2.在surface go 2上操作 禁用快速启动 在 Windows 中,禁用“电源选项”中的“快速启动”>选择电源按钮的功能 禁用 Bitlocker 在 Wi…...

Java:SpringMVC的使用(1)
目录第一章、SpringMVC基本了解1.1 概述1.2 SpringMVC处理请求原理简图第二章、SpringMVC搭建框架1、搭建SpringMVC框架1.1 创建工程【web工程】1.2 导入jar包1.3 编写配置文件(1) web.xml注册DispatcherServlet(2) springmvc.xml(3) index.html1.4 编写请求处理器【Controller…...

自动化测试岗位求职简历编写规范+注意事项,让你的简历脱颖而出
目录 前言 1.个人信息 2.教育背景(写最高学历) 3.个人技能(按精通/掌握/熟练/了解层次来写) 4.工作经历 5.工作经验/项目经历 6.自我评价 总结 前言 挑选一个阅读舒适度不错的模板 HR和面试官看的简历多,都是快速阅读,舒适度特别重要;…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
