常见排序算法汇总
排序算法汇总
这篇文章说明下排序算法,直接开始。
1.冒泡排序
最简单直观的排序算法了,新手入门的第一个排序算法,也非常直观,最大的数字像泡泡一样一个个的“冒”到数组的最后面。
算法思想:反复遍历要排序的序列,每次比较相邻的两个元素,如果顺序不正确就交换它们。这样每次遍历都会将最大的元素放到末尾。
排序的时间复杂度O(n²),如果设置标志为(如果发生数据交换flag=1,默认为0)复杂度为O(n),,因为是原地排序,基本不用。
void bubble_sort(vector<int> &nums) {int n = nums.size();for (int i = 0; i < n-1; i++) {for (int j = 0; j < n-i-1; j++) {if (nums[j] > nums[j+1]) {swap(nums[j], nums[j+1]);}}}
}
2.选择排序
算法思想:每次从未排序的部分选择最小的元素,放到已排序部分的末尾,重复这个过程。时间复杂度:O(n²),无论怎样都是O(n²),空间复杂度O(1),基本不用。
void selectionSort(std::vector<int> &arr) {int n = arr.size();for (int i = 0; i < n - 1; ++i) {int minIndex = i; // 假设当前元素为最小值的索引for (int j = i + 1; j < n; ++j) { // 在未排序部分查找最小值if (arr[j] < arr[minIndex]) {minIndex = j; // 更新最小值索引}}// 将找到的最小值与当前元素交换if (minIndex != i) {std::swap(arr[i], arr[minIndex]);}}
}
3.插入排序
算法思想:将数组分为已排序和未排序部分,从未排序部分取元素,在已排序部分找到合适的位置插入。时间复杂度O(n²),空间复杂度O(1)。
void insertionSort(std::vector<int>& arr) {int n = arr.size(); // 获取数组的大小for (int i = 1; i < n; i++) { // 从第二个元素开始int key = arr[i]; // 当前待插入的元素int j = i - 1;// 在已排序部分中找到合适的位置插入 keywhile (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j]; // 向后移动元素j--; // 移动到前一个元素}arr[j + 1] = key; // 插入 key}
}
4.快速排序
算法思想:选择一个基准元素,将数组划分为比基准小的部分和比基准大的部分,递归地对这两个部分排序。时间复杂度O(n log n),空间复杂度O(log n) 。
void fastSort(vector<int> &nums, int low, int high) {if (low >= high)return;int pivot = nums[high], i = low;for (int j = low; j < high; j++) {if (nums[j] < pivot) {if (i != j)swap(nums[i], nums[j]);i++;}}swap(nums[i], nums[high]);fastSort(nums, low, i - 1);fastSort(nums, i + 1, high);
}
5.归并排序
算法思想:采用分治法,将数组分成两个子数组分别排序,再将它们合并成一个有序数组。时间复杂度O(n log n),空间复杂度O(n) 。
//递归版本
void mergeSort(vector<int> &nums, int left, int right) {if (left >= right)return;int mid = left + (right - left)/2;mergeSort(nums, left, mid);mergeSort(nums, mid + 1, right);vector<int> tmp(right - left + 1);int count = 0;int i = left, j = mid + 1;while (i <= mid && j <= right) {if (nums[i] < nums[j]) {tmp[count++] = nums[i++];} else {tmp[count++] = nums[j++];}}while (i <= mid) {tmp[count++] = nums[i++];}while (j <= right) {tmp[count++] = nums[j++];}for (int p = 0; p < tmp.size(); p++) {nums[left + p] = tmp[p];}
}
//迭代版本
void mergeSortIterative(std::vector<int> &nums) {int n = nums.size();for (int currentsize = 1; currentsize < n - 1; currentsize *= 2)for (int left = 0; left < n - 1; left += 2 * currentsize) {int mid = min(left + currentsize - 1, n - 1);int right = min(left + 2 * currentsize - 1, n - 1);int n1 = mid - left + 1;int n2 = right - mid;vector<int> leftArr(n1), rightArr(n2);for (int i = 0; i < n1; i++)leftArr[i] = nums[left + i];for (int i = 0; i < n2; i++)rightArr[i] = nums[mid + i + 1];int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (leftArr[i] < rightArr[j]) {nums[k] = leftArr[i++];} else {nums[k] = rightArr[j++];}k++;}while (i < n1) {nums[k++] = leftArr[i++];}while (j < n2) {nums[k++] = rightArr[j++];}}
}
6.堆排序
算法思想:使用二叉堆这种数据结构,先构建最大堆(或最小堆),然后依次将堆顶元素移除,重新调整堆。时间复杂度O(n log n),空间复杂度O(1)(不用递归的话)
void heapify(vector<int> &nums, int n, int i) {if(i>n)return;int largest = i;int left = 2 * i + 1, right = 2 * i + 2;if (left < n && nums[left] > nums[largest])largest = left;if (right < n && nums[right] > nums[largest])largest = right;if (largest != i) {swap(nums[i], nums[largest]);heapify(nums, n, largest);}}void heapSort(vector<int> &nums) {int n = nums.size();for(int i=n/2-1;i>=0;i--) {heapify(nums,n,i);}for(int i=n-1;i>0;i--) {swap(nums[0],nums[i]);heapify(nums,i,0);}
}
排序算法的总结表格:
| 排序算法 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n²) | O(n²) | O(1) | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 |
| 插入排序 | O(n) | O(n²) | O(n²) | O(1) | 稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
| 快速排序 | O(n log n) | O(n²) | O(n log n) | O(log n) | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 不稳定 |
7.文末解释一下算法时间复杂中的log n,有些人不理解
快速排序的平均时间复杂度为 O(n log n),是因为它在理想情况下可以将问题规模递归减半,而每次递归的划分过程需要 O(n) 的操作。通过递归树的结构,我们可以直观理解为什么时间复杂度为 O(n log n)。
1. 每一层的操作需要 O(n) 的时间
在快速排序的每一层递归中,主要的开销来自于划分(partition)操作。这个操作的过程是选取一个基准元素(pivot),然后从两边扫描数组,交换元素,使得基准元素的左边都比它小,右边都比它大。
无论基准元素选得如何,每次划分需要遍历整个数组。因此,在每一层递归中,划分操作的时间复杂度是 O(n),其中 n 是当前数组的长度。
2. 递归的层数为 log n
在理想情况下,快速排序的每次递归都能将数组大致划分为相等的两部分,即每次递归之后,数组的规模缩小为原来的 1/2。这个过程相当于将问题规模递归地减半,直到数组大小缩减到 1。
因此,总共需要递归 log n 层(递归树的高度),这里的 log n 表示递归树的层数,也就是快速排序的递归深度。
3. 总时间复杂度为 O(n log n)
- 每层的时间复杂度:在递归树的每一层,需要
O(n)的时间来对数组进行划分。 - 递归树的层数:递归树的高度为
log n,表示总共要递归log n层。
因此,整个快速排序的总时间复杂度就是:
总时间=每层所需的时间×递归的层数=O(n)×O(logn)=O(nlogn)
递归树示意:
可以将快速排序的递归过程看作是一个递归树,每一层是对整个数组的遍历,每一层都需要 O(n) 的时间来进行划分。递归树的层数是 log n,总共 log n 层。
举例说明递归树结构:
O(n)----------------| |O(n/2) O(n/2)------- -------| | | |O(n/4) O(n/4) O(n/4) O(n/4)----------------------------... (共 log n 层)
4. 平均时间复杂度为 O(n log n) 的解释
在理想情况下,每次划分都能把数组平分成两半,快速排序的递归树的高度为 log n。每一层递归处理的元素总数为 n(即整个数组的长度),由于有 log n 层,所以整个快速排序的总时间复杂度为 O(n log n)。
5. 总结:
- 每一层快速排序的递归操作需要
O(n)的时间来进行划分。 - 总共有
log n层递归,即递归树的高度为log n。 - 因此,快速排序的平均时间复杂度是
O(n log n)。
不过需要注意,在最坏情况下(当每次划分都极不平衡,如数组是完全有序的),递归树的高度会退化为 n,此时时间复杂度为 O(n^2)。通过随机化选择基准元素,可以有效避免这种最坏情况的发生,从而保证平均时间复杂度为 O(n log n)。
相关文章:

常见排序算法汇总
排序算法汇总 这篇文章说明下排序算法,直接开始。 1.冒泡排序 最简单直观的排序算法了,新手入门的第一个排序算法,也非常直观,最大的数字像泡泡一样一个个的“冒”到数组的最后面。 算法思想:反复遍历要排序的序列…...

Golang | Leetcode Golang题解之第459题重复的子字符串
题目: 题解: func repeatedSubstringPattern(s string) bool {return kmp(s s, s) }func kmp(query, pattern string) bool {n, m : len(query), len(pattern)fail : make([]int, m)for i : 0; i < m; i {fail[i] -1}for i : 1; i < m; i {j : …...

0.计网和操作系统
0.计网和操作系统 熟悉计算机网络和操作系统知识,包括 TCP/IP、UDP、HTTP、DNS 协议等。 常见的页面置换算法: 先进先出(FIFO)算法:将最早进入内存的页面替换出去。最近最少使用(LRU)算法&am…...

探索Prompt Engineering:开启大型语言模型潜力的钥匙
前言 什么是Prompt?Prompt Engineering? Prompt可以理解为向语言模型提出的问题或者指令,它是激发模型产生特定类型响应的“触发器”。 Prompt Engineering,即提示工程,是近年来随着大型语言模型(LLM,Larg…...
)
滚雪球学Oracle[3.3讲]:数据定义语言(DDL)
全文目录: 前言一、约束的高级使用1.1 主键(Primary Key)案例演示:定义主键 1.2 唯一性约束(Unique)案例演示:定义唯一性约束 1.3 外键(Foreign Key)案例演示:…...

ssrf学习(ctfhub靶场)
ssrf练习 目录 ssrf类型 漏洞形成原理(来自网络) 靶场题目 第一题(url探测网站下文件) 第二关(使用伪协议) 关于http和file协议的理解 file协议 http协议 第三关(端口扫描)…...

ElasticSearch之网络配置
对官方文档Networking的阅读笔记。 ES集群中的节点,支持处理两类通信平面 集群内节点之间的通信,官方文档称之为transport layer。集群外的通信,处理客户端下发的请求,比如数据的CRUD,检索等,官方文档称之…...

【C语言进阶】系统测试与调试
1. 引言 在开始本教程的深度学习之前,我们需要了解整个教程的目标及其结构,以及为何进阶学习是提升C语言技能的关键。 目标和结构: 教程目标:本教程旨在通过系统化的学习,从单元测试、系统集成测试到调试技巧…...

多个单链表的合成
建立两个非递减有序单链表,然后合并成一个非递增有序的单链表。 注意:建立非递减有序的单链表,需要采用创建单链表的算法 输入格式: 1 9 5 7 3 0 2 8 4 6 0 输出格式: 9 8 7 6 5 4 3 2 1 输入样例: 在这里给出一组输入。例如…...

『建议收藏』ChatGPT Canvas功能进阶使用指南!
大家好,我是木易,一个持续关注AI领域的互联网技术产品经理,国内Top2本科,美国Top10 CS研究生,MBA。我坚信AI是普通人变强的“外挂”,专注于分享AI全维度知识,包括但不限于AI科普,AI工…...

Ollama 运行视觉语言模型LLaVA
Ollama的LLaVA(大型语言和视觉助手)模型集已更新至 1.6 版,支持: 更高的图像分辨率:支持高达 4 倍的像素,使模型能够掌握更多细节。改进的文本识别和推理能力:在附加文档、图表和图表数据集上进…...

gdb 调试 linux 应用程序的技巧介绍
使用 gdb 来调试 Linux 应用程序时,可以显著提高开发和调试的效率。gdb(GNU 调试器)是一款功能强大的调试工具,适用于调试各类 C、C 程序。它允许我们在运行程序时检查其状态,设置断点,跟踪变量值的变化&am…...

Java项目实战II基于Java+Spring Boot+MySQL的房产销售系统(源码+数据库+文档)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者 一、前言 随着房地产市场的蓬勃发展,房产销售业务日益复杂,传统的手工管理方式已难以满…...

aws(学习笔记第一课) AWS CLI,创建ec2 server以及drawio进行aws画图
aws(学习笔记第一课) 使用AWS CLI 学习内容: 使用AWS CLI配置密钥对创建ec2 server使用drawio(vscode插件)进行AWS的画图 1. 使用AWS CLI 注册AWS账号 AWS是通用的云计算平台,可以提供ec2,vpc,SNS以及clo…...

【Python】Eventlet 异步网络库简介
Eventlet 是一个 Python 的异步网络库,它使用协程(green threads)来简化并发编程。通过非阻塞的 I/O 操作,Eventlet 使得你可以轻松编写高性能的网络应用程序,而无需处理复杂的回调逻辑或编写多线程代码。它广泛应用于…...
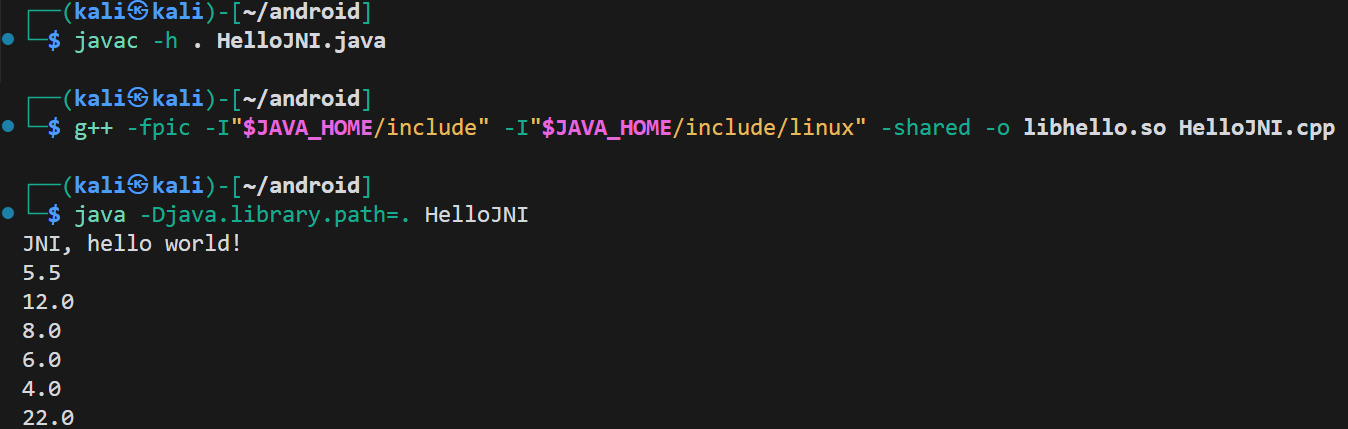
【JNI】数组的基本使用
在上一期讲了基本类型的基本使用,这期来说一说数组的基本使用 HelloJNI.java:实现myArray函数,把一个整型数组转换为双精度型数组 public class HelloJNI { static {System.loadLibrary("hello"); }private native String HelloW…...

React跨平台
React的跨平台应用开发详解如下: 一、跨平台能力 React本身是一个用于构建用户界面的JavaScript库,但它通过React Native等框架实现了跨平台应用开发的能力。React Native允许开发者使用JavaScript和React来编写原生应用,这些应用可以在iOS和…...

如何在 SQL 中更新表中的记录?
当你需要修改数据库中已存在的数据时,UPDATE 语句是你的首选工具。 这允许你更改表中一条或多条记录的特定字段值。 下面我将详细介绍如何使用 UPDATE 语句,并提供一些开发建议和注意事项。 基础用法 假设我们有一个名为 employees 的表,…...

宠物饮水机的水箱低液位提醒如何实现?
ICMAN液位检测芯片轻松实现宠物饮水机的水箱低液位提醒功能! 工作原理 : 基于双通道电容式单点液位检测原理 方案特点: 液位检测精度高达1mm,超强抗干扰,动态CS 10V 为家用电器水位提醒的应用提供了一种简单而又有…...

EXCEL_光标百分比
Public Sub InitCells()Dim iSheet As LongFor iSheet Sheets.Count To 1 Step -1Sheets(iSheet).ActivateActiveWindow.Zoom 85ActiveWindow.ScrollRow 1ActiveWindow.ScrollColumn 1Sheets(iSheet).Range("A1").ActivateNext iSheetEnd Sub对日项目中的文档满天…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
