【笔记】信度检验

一、信度

信度是指测量结果的一致性和稳定性。

1.一致性（Consistency）

一致性指的是测量工具内部各个部分或项目之间的协调一致程度。高一致性意味着测量工具的不同部分都在测量同一个概念或特质。

例子：智力测试

假设我们有一个包含100道题的智力测试，这些题目涵盖了语言、数学、逻辑推理等方面。如果这个测试具有高度的一致性，那么：

• 测试中的所有题目都应该与整体智力水平相关。
• 擅长语言题的人也可能在数学和逻辑推理题上表现良好。
• 如果我们将测试分成两半，两半的得分应该高度相关。

我们可以通过计算Cronbach’s α系数来评估内部一致性。

2.稳定性（Stability）

稳定性指的是测量结果在不同时间点或不同情况下的一致程度。高稳定性意味着测量结果不会因时间或环境的变化而发生显著变化（假设被测量的特质本身没有变化）。

例子：抑郁症量表

假设我们有一个用于评估抑郁症状严重程度的量表。如果这个量表具有高度的稳定性，那么：

• 对同一个人在短时间内（如一周）进行两次测试，两次的得分应该非常接近。
• 即使测试环境有所不同（如在诊所vs在家里），得分也不应有显著差异。

可以通过计算重测信度来评估稳定性。

二、信度检验

信度检验的基本原理：

信度检验基于经典测量理论（Classical Test Theory）。该理论假设观察分数（X）由真实分数（T）和误差分数（E）组成：

$$X=T+E$$

信度（reliability）定义为真实分数方差与观察分数方差的比率：

$$reliability=\frac{{\sigma }_T^2}{{\sigma }_X^2}$$

其中，$${\sigma }_T^2$$ 是真实分数的方差，$${\sigma }_X^2$$ 是观察分数的方差。

1.重测信度（Test-Retest Reliability）

原理：在相近的时间内对同一群体进行两次测量，若结果高度一致，则可靠。

方法：
a) 选取代表性样本
b) 进行第一次测量（T1）
c) 间隔一定时间（通常1-4周）
d) 进行第二次测量（T2）
e) 计算T1和T2的皮尔逊相关系数（r）

评估标准：

• r > 0.9: 极高的信度
• 0.8 < r ≤ 0.9: 良好的信度
• 0.7 < r ≤ 0.8: 可接受的信度
• r ≤ 0.7: 信度不足，需要改进

2.内部一致性信度（Internal Consistency Reliability）

原理：项目间应该具有较高的一致性。

最常用的方法是Cronbach’s α系数：

$$\alpha =\frac{k}{k-1}(1-\frac{{\sum }_{i=1}^k{\sigma }_i^2}{{\sigma }_X^2})$$

其中，k是项目数量，$${\sigma }_i^2$$ 是第i个项目的方差，$${\sigma }_X^2$$ 是总分方差。

步骤：
a) 收集数据
b) 计算各项目得分与总分的相关
c) 计算Cronbach’s α系数

评估标准：

• α > 0.9: 优秀
• 0.8 < α ≤ 0.9: 良好
• 0.7 < α ≤ 0.8: 可接受
• 0.6 < α ≤ 0.7: 有争议
• α ≤ 0.6: 不可接受

3.分半信度（Split-Half Reliability）

原理：如果测量工具是可靠的，那么将其分成两半后，两半之间应该具有高度一致性。

步骤：
a) 将测量工具随机分为两半
b) 分别计算两半的得分
c) 计算两半得分的相关系数（r）
d) 使用Spearman-Brown公式校正：

$$r_{corrected}=\frac{2r}{1+r}$$

评估标准与重测信度相似。

4.评分者间信度（Inter-rater Reliability）

原理：用于评估多个评分者之间的一致性程度。

方法：

• 对于类别变量：使用Kappa系数
• 对于连续变量：使用组内相关系数（Intraclass Correlation Coefficient, ICC）

步骤：
a) 选取样本
b) 多个评分者独立评分
c) 计算评分者间的一致性系数

评估标准因具体使用的系数而异，通常0.7以上被认为是可接受的。

三、SPSS实操

1.内部一致性信度（Cronbach’s α）

a) 打开SPSS，导入 ‘reliability_test_data.csv’ 文件。

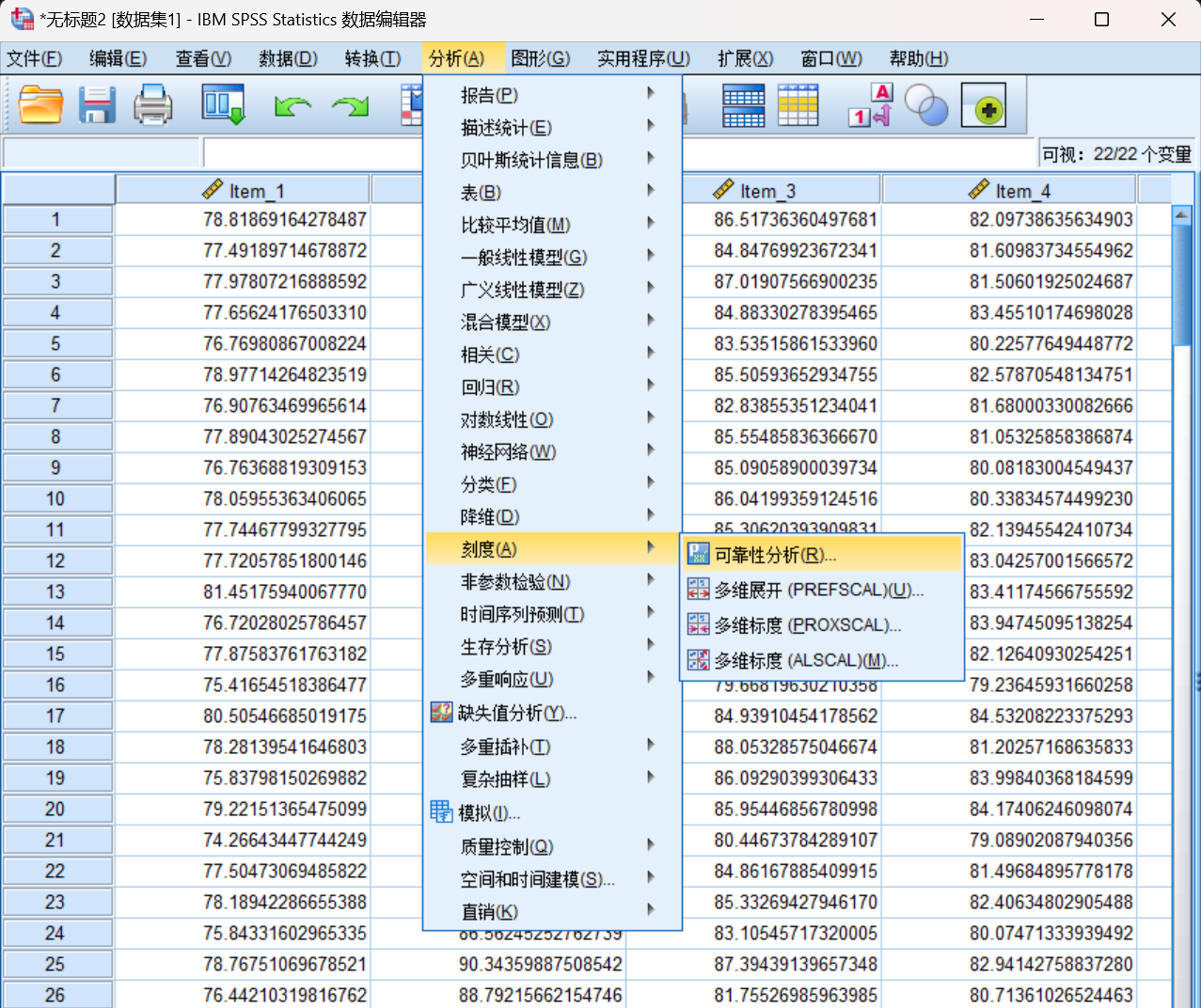
b) 选择菜单：分析 -> 刻度 -> 可靠性分析。

c) 将Item_1到Item_10移到"项"框中。

d) 在"统计"按钮中，选择"项的标度"和"删除项后的标度"。

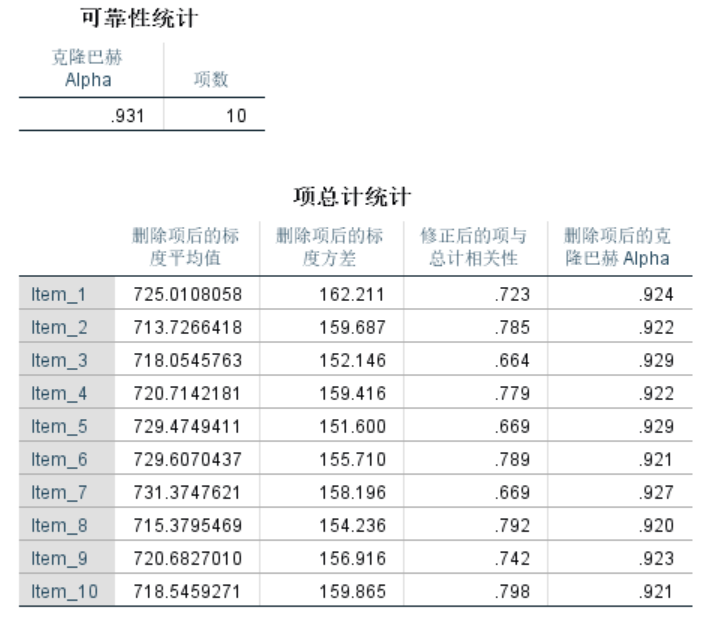
e) 点击"确定"运行分析,，得到Cronbach’s α系数值。

查看Cronbach’s α系数。通常0.7以上被认为是可接受的，0.8以上是良好的，0.9以上是优秀的。

2.重测信度

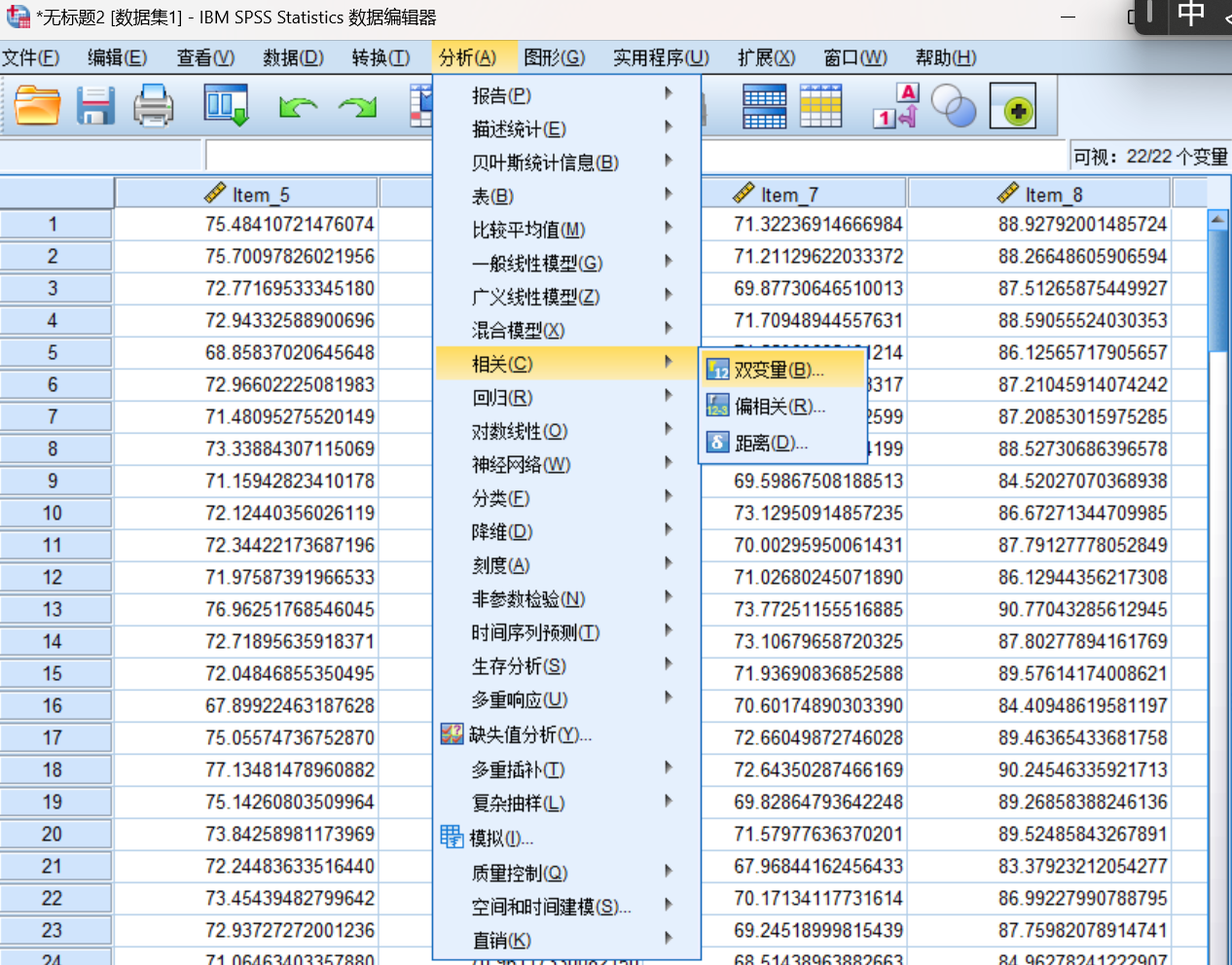
a) 选择菜单：分析 -> 相关 -> 双变量。

b) 将Item_1到Item_10和相应的Retest_Item_1到Retest_Item_10放入"变量"框。

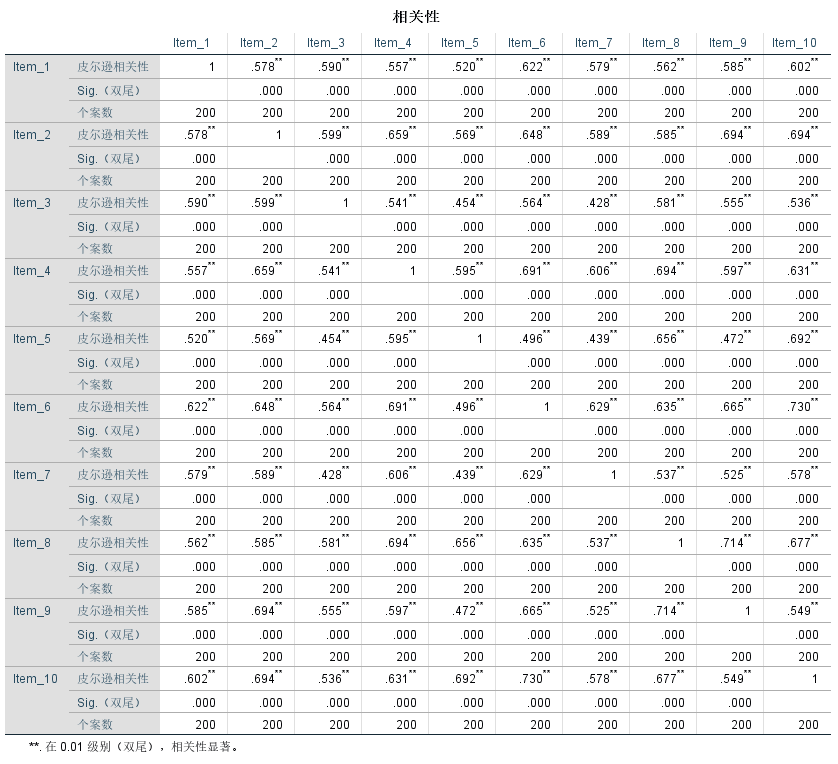
c) 选择"Pearson"相关系数，确保进行双侧检验并标记显著性相关。

d) 点击"确定"运行分析。

查看每个项目的原始测试和重测之间的相关系数。通常0.7以上被认为是可接受的，越接近1越好。

3.分半信度：

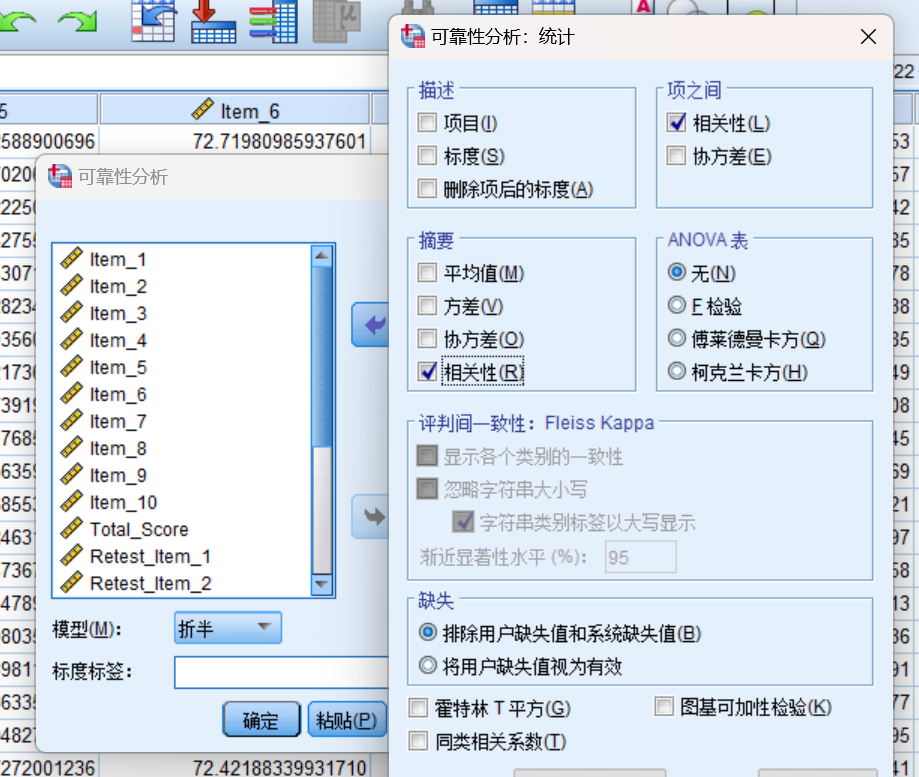
a) 选择菜单：分析 -> 量表 -> 可靠性分析。

b) 将Item_1到Item_10移到"项"框中。

c) 点击"统计量"按钮，选中"尺度"下的"相关"和"分半"选项。

d) 点击"确定"运行分析。

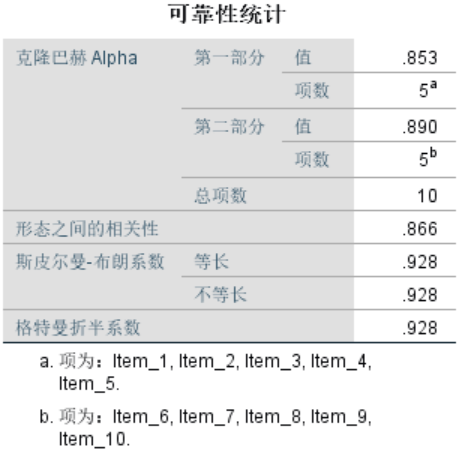
查看Spearman-Brown系数。解释标准与重测信度相似。

4.组内相关系数（ICC，用于评分者间信度模拟）：

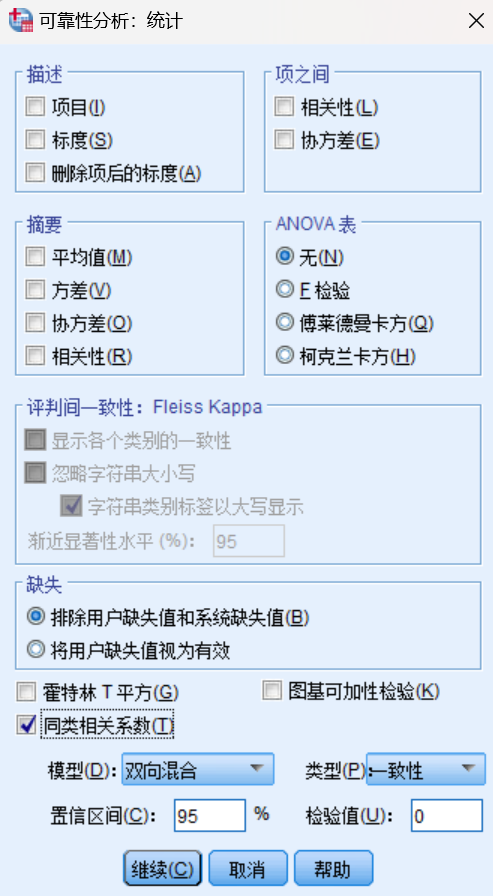
1. 点击菜单栏的"分析" > “刻度” > “可靠性分析”。
2. 点击"模型"按钮:
   • 选择"双向随机"(如果评分者是随机选择的)或"双向混合"(如果评分者是固定的)。
   • 选择"一致性"或"绝对一致"定义。通常选择"一致性"。
3. 点击"统计量"按钮:
   • 选择置信区间水平(通常为95%)。
4. 点击"继续"返回主对话框,然后点击"确定"运行分析。
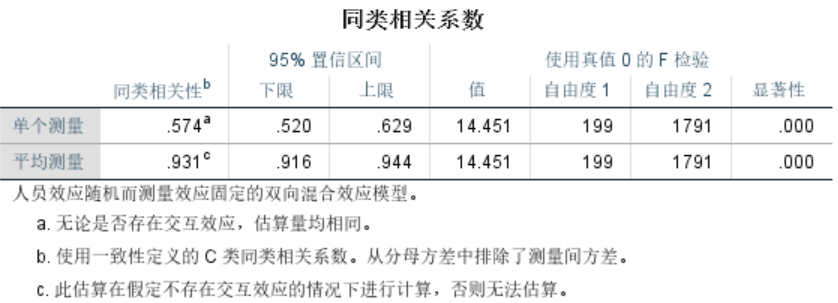
5. 结果输出: SPSS将生成一个包含ICC值、置信区间和F检验结果的输出表。

解释结果:

• ICC值范围从0到1,越接近1表示评分者间一致性越高。
• 通常认为ICC > 0.75表示良好到优秀的一致性,0.60-0.74为中等,< 0.60为差。
• 查看置信区间和F检验的p值来评估结果的统计显著性。