第18场小白入门赛(蓝桥杯)
第 18 场 小白入门赛
6 武功秘籍
考察进制理解。
对于第 i i i 位,设 b i t i = x bit_i=x biti=x ,每一位的最大值是 b j b_j bj ,也就是说每一位是 b j + 1 b_j+1 bj+1 进制 ,那么第 i i i 位的大小就是 x × ∑ j = i + 1 l a s ( b j + 1 ) x\times \sum_{j=i+1}^{las} (b_j+1) x×∑j=i+1las(bj+1) 。
据此推导。
#include<bits/stdc++.h>
using namespace std;
#define int long longvoid solve(){int n, k;cin >> n >> k;if(k == 1){cout << "0\n";return ;}-- k;vector<int> bit;while(n){bit.push_back(n % 10);n /= 10;}vector<int> t(bit.size() + 1);// for(auto &x : bit) cout << x << ' '; cout << '\n';int l, r = 0, lasBit = 0;t[0] = 1;for(int i = 0; i < bit.size(); i ++){l = r + 1;r += t[i] * bit[i];if(r >= k){lasBit = i;break;}// cout << i << ' ' << l << ' ' << r << '\n';t[i + 1] = t[i] * (bit[i] + 1);}// cout << lasBit << '\n';for(int i = lasBit; i >= 0; i --){cout << (k / t[i]);k %= t[i];}
}signed main(){// ios::sync_with_stdio(false);// cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T --){solve();}return 0;
}
2 + 4 情报传递
思维题,技巧在于具有大量相同的区间,实际上只有左右两个特殊区间,以及中间大量相同的区间。
首先,如果不存在点不能走,那么从 x x x 走到 y y y ,贪心走 ⌈ y − x 2 ⌉ \lceil \frac {y-x}{2} \rceil ⌈2y−x⌉ 即可。
假设在 a → b a\rightarrow b a→b 区间内,存在 x x x 个 c c c 的倍数,设 d d d 是这些点的最小值, e e e 是最大值。
那么从 a → d − 1 a\rightarrow d-1 a→d−1 和 e + 1 → b e+1\rightarrow b e+1→b 贪心走即可。
剩下的全是相同的走法。
O ( 1 ) O(1) O(1) 。
dp 思路很简答,爬楼梯问题, O ( n ) O(n) O(n) 。
Trick :
第一个 ≥ x \geq x ≥x 的 c c c 的倍数 : ⌈ x c ⌉ × c \lceil \frac x c \rceil \times c ⌈cx⌉×c
第一个 ≤ x \leq x ≤x 的 c c c 的倍数 : ⌊ x c ⌋ × c \lfloor \frac x c \rfloor \times c ⌊cx⌋×c
#include<bits/stdc++.h>
using namespace std;
#define int long longint dis(int a, int b){return (b - a) / 2 + (b - a) % 2;
}void solve(){int a, b, c, x = 0;cin >> a >> b >> c;int d = (a + c - 1) / c * c; // 第一个 >= a 的 c 的倍数int e = b / c * c; // 第一个 <= b 的 c 的倍数if(d > b){ cout << dis(a, b) << '\n';}else{cout << dis(a, d - 1) + dis(e + 1, b) + 1 + dis(1, c + 1) * ((e - d) / c) << '\n';}
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T = 1;cin >> T;while (T --){solve();}return 0;
}
3 村长分钱
已知 a , b a,b a,b , 求满足 a m o d y = b a \bmod y=b amody=b ,多少 y y y 满足要求
即 a = b + x y a=b+xy a=b+xy 。
即 x y = b − a xy=b-a xy=b−a ,计算一下 b − a b-a b−a 有多少因子即可。
注意只统计 > b >b >b 的因子。
#include <iostream>
#include <cmath>
using namespace std;int count_solutions(int a, int b) {if (a < b) return 0; // 无解的情况int d = a - b;int count = 0;// 枚举 d 的因数for (int x = 1; x * x <= d; ++x) {if (d % x == 0) {if (x > b) count++; // x 是 d 的因数,且 x > bif (d / x != x && d / x > b) count++; // d/x 也是因数,且 d/x > b}}return count;
}int main() {int a, b;cin >> a >> b;cout << count_solutions(a, b) << endl;return 0;
}
5 好汉身份
假设先手的回合,发现选择 a + b a+b a+b 小的更优。
发现后手同样如此。
#include<bits/stdc++.h>
using namespace std;
#define int long longstruct node{int a, b;bool operator < (const node & T) const {return a + b < T.a + T.b;}
}v[2100];int n;void solve(){cin >> n;n <<= 1;for(int i = 1; i <= n; i ++){cin >> v[i].a;}for(int i = 1; i <= n; i ++){cin >> v[i].b;}sort(v + 1, v + n + 1);int res = 0; for(int i = 1; i <= n; i ++){if(i & 1) res += v[i].a;else res -= v[i].b;}cout << res;
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T = 1;// cin >> T;while (T --){solve();}return 0;
}
相关文章:
)
第18场小白入门赛(蓝桥杯)
第 18 场 小白入门赛 6 武功秘籍 考察进制理解。 对于第 i i i 位,设 b i t i x bit_ix bitix ,每一位的最大值是 b j b_j bj ,也就是说每一位是 b j 1 b_j1 bj1 进制 ,那么第 i i i 位的大小就是 x ∑ j i 1…...
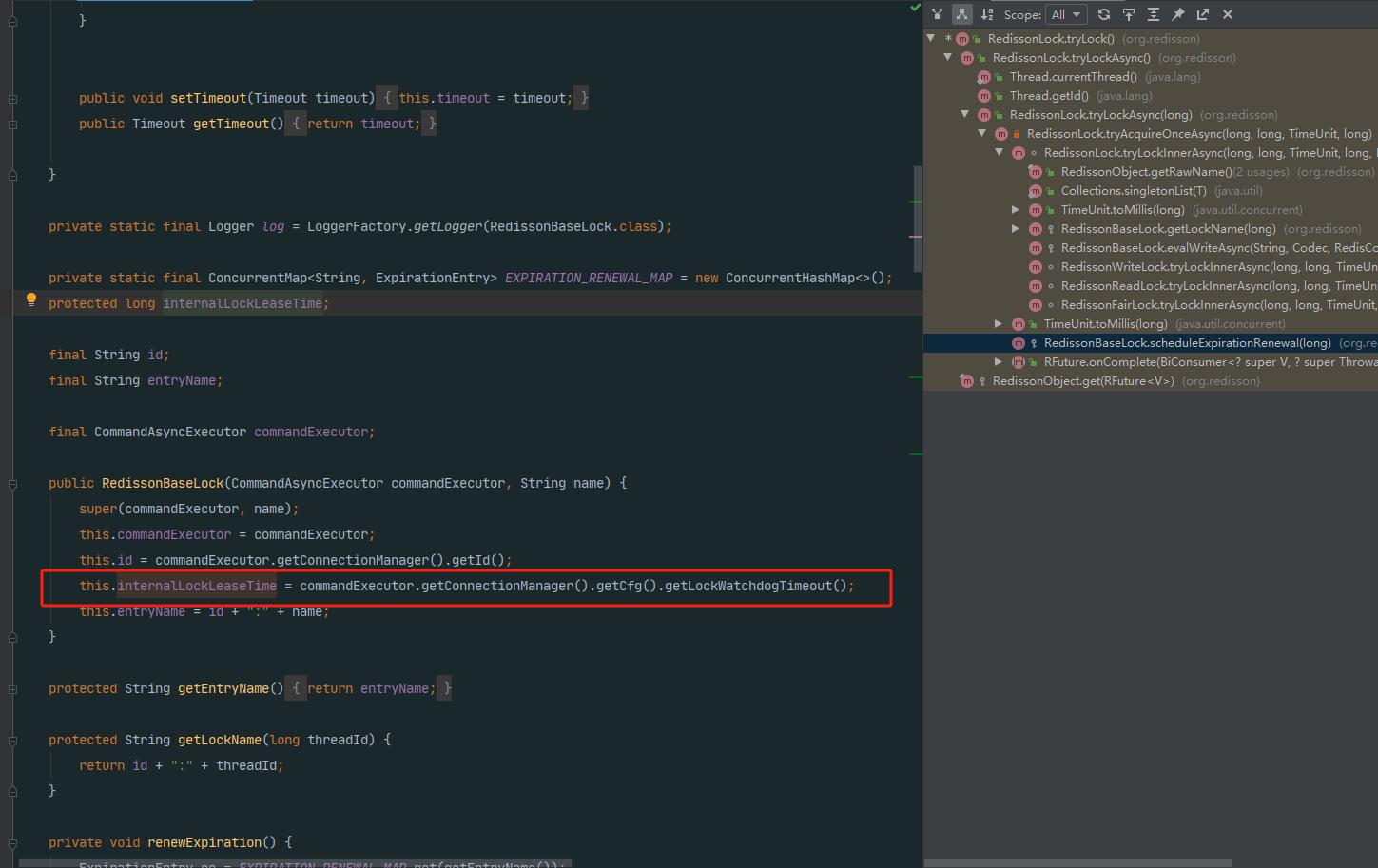
Redission · 可重入锁(Reentrant Lock)
前言 Redisson是一个强大的分布式Java对象和服务库,专为简化在分布式环境中的Java开发而设计。通过Redisson,开发人员可以轻松地在分布式系统中共享数据、实现分布式锁、创建分布式对象,并处理各种分布式场景的挑战。 Redisson的设计灵感来…...

初阶C语言-指针
1.指针是什么? 理解指针的两个要点: 1.指针是内存中一个最小单元的编号,也就是地址 2.口头语中说的指针,通常是指指针变量,是用来存放内存地址的变量 总结:指针就是地址,口语中说的指针通常是指…...

论文笔记:微表情欺骗检测
整理了AAAI2018 Deception Detection in Videos 论文的阅读笔记 背景模型实验可视化 背景 欺骗在我们的日常生活中很常见。一些谎言是无害的,而另一些谎言可能会产生严重的后果。例如,在法庭上撒谎可能会影响司法公正,让有罪的被告逍遥法外。…...

智能家居有哪些产品?生活中常见的人工智能有哪些?
智能家居有哪些产品? 1、智能照明设备类:智能开关、智能插座、灯控模块、智能空开、智能灯、无线开关。 2、家庭安防类:智能门锁、智能摄像机、智能猫眼、智能门铃。 3、智能传感器类:烟雾传感器、可燃气体传感器、水浸传感器、声光报警器…...

洗车行软件系统有哪些 佳易王洗车店会员管理系统操作教程#洗车店会员软件试用版下载
一、前言 【试用版软件下载可点击本文章最下方官网卡片】 洗车行软件系统有哪些 佳易王洗车店会员管理系统操作教程#洗车店会员软件试用版下载 洗车管理软件应用是洗车业务的得力助手,实现会员管理及数据统计一体化,助力店铺高效、有序运营。 洗车项…...

【Java】springboot 项目中出现中文乱码
在刚创建的springboot项目中,出现乱码,跟走着解决一下 1、Ctrl Shift S 打开idea设置,根据图片来,将③④这三个地方都修改为UTF-8 2、返回配置查看,解决...

开放式耳机是什么意思?漏音吗?开放式的运动蓝牙耳机推荐
目前运动耳机市场主要分为入耳式、骨传导和开放式三类。入耳式耳机占比30%-40%,虽目前占比较大,但因在运动场景下有闷塞感、出汗不适、屏蔽外界环境音带来安全隐患等缺点,占比会逐渐下降。 骨传导耳机占比也为30%-40%,其不堵塞耳…...

如何优雅的处理NPE问题?
1.什么是NPE? NPE,即NullPointerException,是开发中最常见的问题之一,有必要知道如何正确地处理NPE。 对于 Java 开发者来说,null 是一个令人头疼的类型,一不小心就会发生 NPE (空指针…...

k8s 中存储之 NFS 卷
目录 1 NFS 卷的介绍 2 NFS 卷的实践操作 2.1 部署一台 NFS 共享主机 2.2 在所有k8s节点中安装nfs-utils 2.3 部署nfs卷 2.3.1 生成 pod 清单文件 2.3.2 修改 pod 清单文件增加 实现 NFS卷 挂载的 参数 2.3.3 声明签单文件并查看是否创建成功 2.3.4 在 NFS 服务器 创建默认发布…...

Redis中BitMap实现签到与统计连续签到功能
服务层代码 //签到Overridepublic Result sign() {//1.获取当前登录的用户Long userId UserHolder.getUser().getId();//获取日期LocalDateTime now LocalDateTime.now();//拼接keyString keySuffix now.format(DateTimeFormatter.ofPattern(":yyyyMM"));String …...
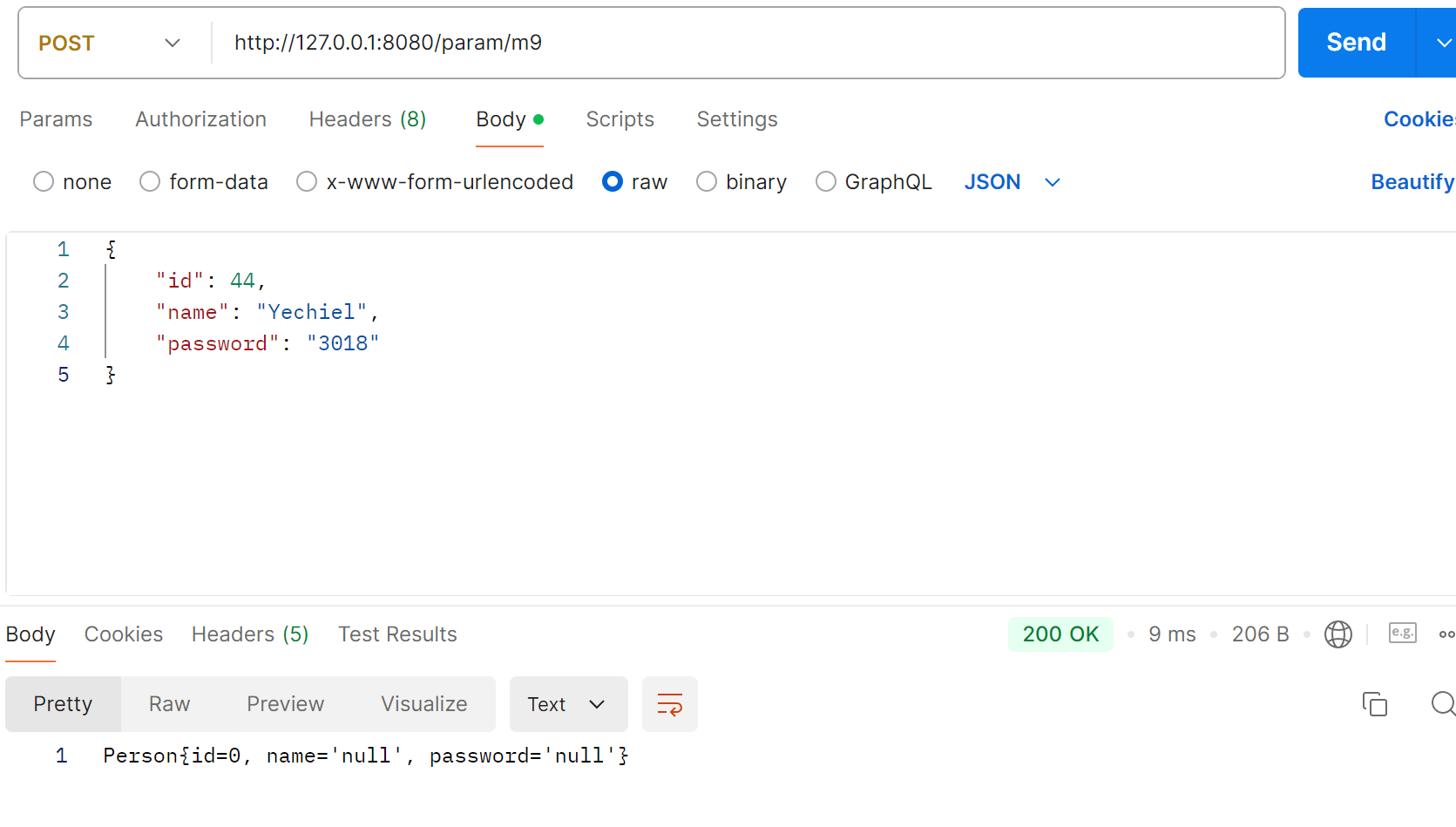
【Spring】“请求“ 之传递 JSON 数据
文章目录 JSON 概念JSON 语法JSON 的语法JSON 的两种结构 JSON 字符串和 Java 对象互转JSON 优点传递 JSON 对象 JSON 概念 JSON:JavaScript Object Notation【JavaScript 对象表示法】 JSON 就是一种数据格式,有自己的格式和语法,使用文本…...

文心一言 VS 讯飞星火 VS chatgpt (359)-- 算法导论24.3 1题
一、在图 24-2上运行Dijkstra算法,第一次使用结点 s s s作为源结点,第二次使用结点 z z z作为源结点。以类似于图 24-6 的风格,给出每次while循环后的 d d d值和 π π π值,以及集合 S S S中的所有结点。如果要写代码,…...
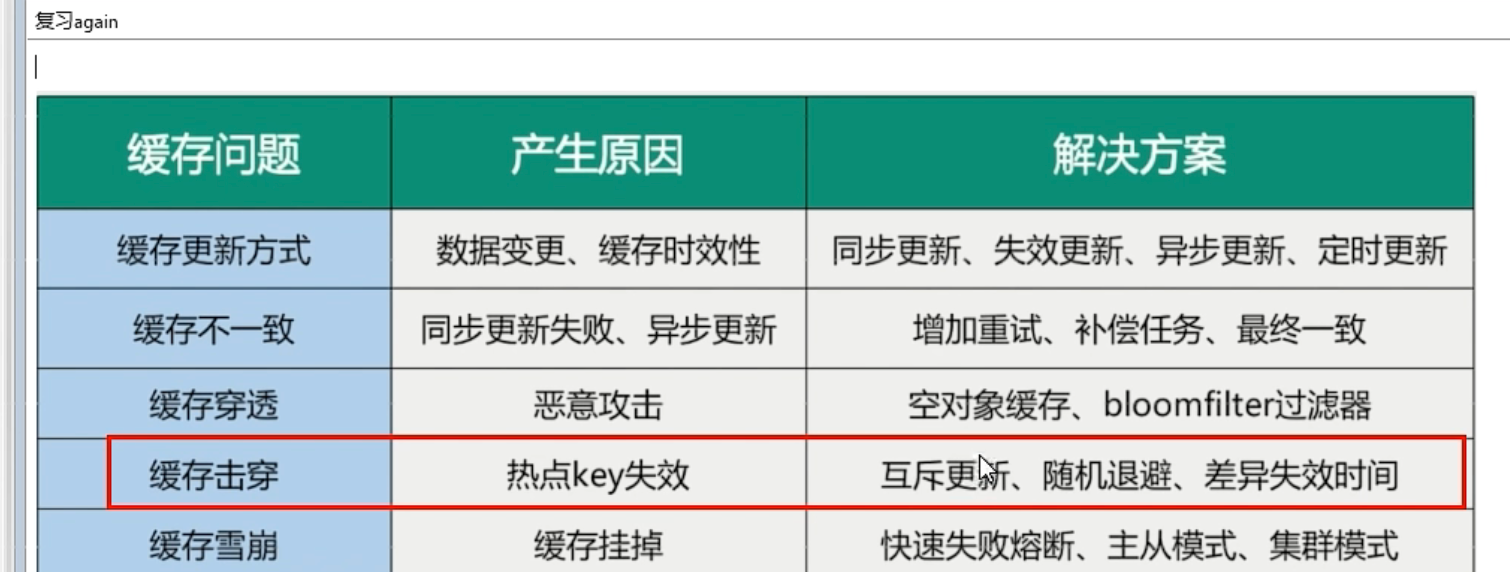
Redis-预热雪崩击穿穿透
预热雪崩穿透击穿 缓存预热 缓存雪崩 有这两种原因 redis key 永不过期or过期时间错开redis 缓存集群实现高可用 主从哨兵Redis Cluster开启redis持久化aof,rdb,尽快恢复集群 多缓存结合预防雪崩:本地缓存 ehcache redis 缓存服务降级&…...

jvisualvm学习
系列文章目录 JavaSE基础知识、数据类型学习万年历项目代码逻辑训练习题代码逻辑训练习题方法、数组学习图书管理系统项目面向对象编程:封装、继承、多态学习封装继承多态习题常用类、包装类、异常处理机制学习集合学习IO流、多线程学习仓库管理系统JavaSE项目员工…...

Gazebo环境下开源UAV与USV联合仿真平台
推荐一个ROS2下基于Gazebo环境的开源UAV与USV联合仿真平台。平台是由两个开源项目共同搭建的。首先是UAV仿真平台,是基于PX4官方仿真平台(https://docs.px4.io/main/en/sim_gazebo_gz);其次是USV仿真平台,是基于VRX仿真…...

Linux进程调度和进程切换
并行(Parallel) 含义:并行是指多个任务在同一时刻同时执行。 硬件要求:需要多个处理器(如多核CPU)或者多台计算设备来实现,这些执行单元能够真正地同时处理不同的任务。例如,一个具…...

机器学习基本上就是特征工程——《特征工程训练营》
作为机器学习流程的一部分,特征工程是对数据进行转化以提高机器学习性能的艺术。 当前有关机器学习的讨论主要以模型为中心。更应该关注以数据为中心的机器学习方法。 本书旨在介绍流行的特征工程技术,讨论何时以及如何运用这些技术的框架。我发现&…...

Android Framework AMS(01)AMS启动及相关初始化1-4
该系列文章总纲链接:专题总纲目录 Android Framework 总纲 本章关键点总结 & 说明: 说明:本章节主要涉及systemserver启动AMS及初始化AMS相关操作。同时由于该部分内容分析过多,因此拆成2个章节,本章节是第一章节&…...

基于基于微信小程序的社区订餐系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...
