排序算法之——归并排序,计数排序
文章目录
- 前言
- 一、归并排序
- 1. 归并排序的思想
- 2. 归并排序时间复杂度及空间复杂度
- 3. 归并排序代码实现
- 1)递归版本
- 2)非递归版本
- 二、计数排序
- 1. 计数排序的思想
- 2. 计数排序的时间复杂度及空间复杂度
- 3. 计数排序代码实现
- 总结(排序算法稳定性)
前言
今天我们一起来了解归并排序(MergeSort),以及一种非比较的计数排序(CountSort)~

一、归并排序
1. 归并排序的思想
归并排序(Merge Sort)是一种基于分治法(Divide and Conquer)的高效排序算法。它的核心步骤包括将一个数组分割成更小的子数组,对这些子数组进行排序,然后将它们合并成一个有序的数组。以下是归并排序的核心步骤详解:
归并排序的核心步骤:
-
分割(Divide):
- 将待排序数组从中间分割成两个子数组(通常是左半部分和右半部分)。
- 继续递归地将这两个子数组再分割,直到每个子数组的大小为 1(即只有一个元素),因为一个元素的数组是有序的。
-
归并(Merge):
- 将两个有序的子数组合并成一个有序的数组。
- 使用两个指针分别指向两个子数组的开头,比较指针指向的元素,将较小的元素放入新数组中,并移动相应的指针。
- 当其中一个子数组的元素被全部放入新数组后,将另一个子数组剩余的元素直接复制到新数组的后面。
-
组合(Combine):
- 在归并的过程中,逐步形成更大的有序数组,最终得到一个完整的有序数组。
总结:
归并排序是一种高效的排序算法,利用分治法的思想,通过将大问题分解为小问题来解决。其稳定性、时间复杂度 O(n log n) 以及适用于大规模数据的特性使其在实际应用中非常流行。
我们一起来看下面的图:

通过这张图我们可以很直观的感受到归并排序的分解和合并过程,它的步骤是这样的:
归并排序步骤总结 :
-
定义归并排序主函数:
MergeSort函数接受待排序数组和数组的大小作为参数。- 在函数中分配一个临时数组
tmp,用于辅助合并数组。其实我们合并出来的数据是在tmp中的,最后拷贝回去。 - 调用
_MergeSort函数进行排序。
void MergeSort(int* arr, int n) {int* tmp = (int*)malloc(sizeof(int) * n); // 创建临时数组_MergeSort(arr, 0, n - 1, tmp); // 调用归并排序free(tmp); // 释放临时数组 } -
定义归并排序递归函数:
_MergeSort函数接受数组、左边界、右边界和临时数组作为参数。- 基本情况:如果
left大于或等于right,则返回,表示该子数组已经有序。
void _MergeSort(int* arr, int left, int right, int* tmp) {if (left >= right) {return; // 基本情况}... } -
分割数组:
- 计算中间索引
mid,将数组分割为左右两个部分。 - 递归调用
_MergeSort对左半部分(left到mid)和右半部分(mid + 1到right)进行排序。

对于它的每一个左右两侧都要继续分割(以左侧为例):

int mid = (left + right) / 2; _MergeSort(arr, left, mid, tmp); // 递归排序左半部分 _MergeSort(arr, mid + 1, right, tmp); // 递归排序右半部分 - 计算中间索引
-
合并有序子数组:
- 定义两个指针
begin1和begin2,分别指向左子数组和右子数组的起始位置。 - 使用
index指针在临时数组tmp中进行合并。

int begin1 = left, end1 = mid; // 左子数组范围 int begin2 = mid + 1, end2 = right; // 右子数组范围 int index = begin1; // 临时数组下标while (begin1 <= end1 && begin2 <= end2) {if (arr[begin1] < arr[begin2]) {tmp[index++] = arr[begin1++]; // 复制较小的元素} else {tmp[index++] = arr[begin2++];} } - 定义两个指针
-
处理剩余元素:
- 如果左子数组还有剩余元素,将其复制到
tmp中。 - 如果右子数组还有剩余元素,也将其复制到
tmp中。
while (begin1 <= end1) {tmp[index++] = arr[begin1++]; // 复制左子数组剩余元素 } while (begin2 <= end2) {tmp[index++] = arr[begin2++]; // 复制右子数组剩余元素 } - 如果左子数组还有剩余元素,将其复制到
-
将合并结果复制回原数组:
- 将临时数组
tmp中的有序元素复制回原数组arr的相应位置。
for (int i = left; i <= right; i++) {arr[i] = tmp[i]; // 将临时数组的内容复制回原数组 } - 将临时数组
2. 归并排序时间复杂度及空间复杂度
归并排序(Merge Sort)是一种高效的排序算法,其时间复杂度和空间复杂度如下:
时间复杂度 :
- 归并排序的时间复杂度为 O(n log n):
-
分割阶段:每次将数组分成两个子数组,深度为 log n,表示分割的层数。
-
合并阶段:在每一层中,合并两个子数组的过程需要 O(n) 的时间,因为每个元素都要被处理一次。
-
因此,整个算法的时间复杂度可以表示为:

-
根据主定理,得到归并排序的时间复杂度为 O(n log n)。
-
空间复杂度 :
- 归并排序的空间复杂度为 O(n):
- 归并排序需要使用额外的临时数组来存储合并过程中的结果。在每次合并操作中,都会分配一个大小为 n 的临时数组,因此其空间复杂度为 O(n)。
总结 :
- 时间复杂度:O(n log n)
- 空间复杂度:O(n)
3. 归并排序代码实现
1)递归版本
//归并排序
void _MergeSort(int* arr, int left, int right, int* tmp)
{if (left >= right){return;}int mid = (left + right) / 2;_MergeSort(arr, left, mid, tmp);_MergeSort(arr, mid + 1, right, tmp);int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;//index 为tmp下标,不一定是0,而是左边界int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}for (int i = left; i <= right; i++){arr[i] = tmp[i];}
}void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(arr, 0, n - 1, tmp);free(tmp);
}
2)非递归版本
/*
非递归排序与递归排序相反,将一个元素与相邻元素构成有序数组,
再与旁边数组构成有序数组,直至整个数组有序。
要有mid指针传入,因为不足一组数据时,重新计算mid划分会有问题
需要指定mid的位置
*/
void merge(int* a, int left, int mid, int right, int* tmp)
{// [left, mid]// [mid+1, right]int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])tmp[index++] = a[begin1++];elsetmp[index++] = a[begin2++];}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}/*
k用来表示每次k个元素归并
*/
void mergePass(int* arr, int k, int n, int* temp)
{int i = 0;//从前往后,将2个长度为k的子序列合并为1个while (i < n - 2 * k + 1){merge(arr, i, i + k - 1, i + 2 * k - 1, temp);i += 2 * k;}//合并区间[i, n - 1]有序的左半部分[i, i + k - 1]以及不及一个步长的右半部分[i + k, n - 1]if (i < n - k){merge(arr, i, i + k - 1, n - 1, temp);}}
二、计数排序
1. 计数排序的思想
计数排序是一种非比较排序算法,适用于范围有限的整数数据。它的核心思想是利用数组的索引来直接计算元素的位置,达到排序的目的。
1)统计相同元素出现次数
2)根据统计的结果将序列回收到原来的序列
我们来看下面这张图:

这是我们待排序的数组。
- 第一步:定义一个新数组,使得旧数组的元素值是新数组的下标
假设,我们定义成这样行不行?
如果完全按照旧数组的元素值来开空间会造成大量的空间浪费,因此不可取。
这里还有一个问题,如果旧数组的元素值是
负数怎么办呢?
这里空间问题可以和负数问题一起解决:
首先找到旧数组的最小值,以及最大值

遍历一遍数组很容易找到数组最小值为100,最大值为109.
那我们开的空间 range 就是最值差

- 第二步:旧数组中每一个元素减去最小值
min作为新数组下标,出现了几个新数组对应的下标中的元素就是多少,这样也顺便解决了负数问题,因为负数 - 更小的负数 = 正数。

- 第三步:遍历新数组,只要数组数据不为零就循环次数(数组值),输出内容 (i + min),将所有元素拷贝回原来的数组,就完成了排序。

2. 计数排序的时间复杂度及空间复杂度
计数排序是一种有效的排序算法,特别适用于数据范围有限的情况。根据你提供的代码,以下是计数排序的时间复杂度和空间复杂度分析:
时间复杂度:
计数排序的时间复杂度为 O(n + k),其中:
- n:待排序数组的大小。
- k:待排序元素的范围(最大值 - 最小值 + 1)。
分析过程:
- 找最大最小值:遍历数组一次,找到最大值和最小值,时间复杂度为 O(n)。
- 创建计数数组:分配大小为 k 的计数数组,时间复杂度为 O(k)。
- 统计元素出现次数:再次遍历原数组,将每个元素的出现次数记录在计数数组中,时间复杂度为 O(n)。
- 放回排序结果:遍历计数数组,根据记录的次数将元素放回原数组,最坏情况下需要遍历 k 次,时间复杂度为 O(k)。
因此,总的时间复杂度为:

空间复杂度 :
计数排序的空间复杂度为 O(k),其中 k 是待排序元素的范围。
分析过程:
- 需要一个计数数组
count,其大小为 k,用于存储每个元素出现的次数。 - 如果输出数组与原数组相同,空间复杂度会增加到 O(n + k)(包含原数组和计数数组),但通常我们只考虑额外空间,因此空间复杂度通常记为 O(k)。
总结
- 时间复杂度:O(n + k)
- 空间复杂度:O(k)
这种复杂度特性使得计数排序在处理范围有限的整数数据时非常高效。适合用于大规模的正整数排序,尤其在数值分布相对均匀的情况下。
但缺点也很明显,数据过于分散太浪费空间,而且只能处理整数数据!
3. 计数排序代码实现
// 计数排序
void CountSort(int* arr, int n)
{int max = arr[0], min = arr[0];//找最大最小值for (int i = 1; i < n; i++){if (arr[i] > max)max = arr[i];if (arr[i] < min)min = arr[i];}//定义新数组空间大小int range = max - min + 1;int* count = (int*)malloc(range * sizeof(int));if (count == NULL){perror("malloc fail!");exit(1);}//初始化range数组中所有的数据为0memset(count, 0, sizeof(int) * range);//原来的下标成为元素,原来的(元素 - min) 成为下标,出现几次新的元素就加几次for (int i = 0; i < n; i++){count[arr[i] - min]++;}//把排好序的元素放回原数组int index = 0;for (int i = 0; i < range; i++){while (count[i]--){arr[index++] = i + min;}}
}
总结(排序算法稳定性)
到了这里我们所有排序思想已经学完了,再来一起总结一下吧!
排序算法复杂度及稳定性分析:
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的
相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,⽽在排序后的序列中,r[i]仍在r[j]之
前,则称这种排序算法是稳定的;否则称为不稳定的。


谢谢大家~

相关文章:

排序算法之——归并排序,计数排序
文章目录 前言一、归并排序1. 归并排序的思想2. 归并排序时间复杂度及空间复杂度3. 归并排序代码实现1)递归版本2)非递归版本 二、计数排序1. 计数排序的思想2. 计数排序的时间复杂度及空间复杂度3. 计数排序代码实现 总结(排序算法稳定性&am…...

Linux中环境变量
基本概念 环境变量Environmental variables一般是指在操作系统中用来指定操作系统运行环境一些参数。 我们在编写C、C代码时候,在链接的时候从来不知道我们所链接的动态、静态库在哪里。但是还是照样可以链接成功。生成可执行程序。原因就是相关环境变量帮助编译器…...
163页PPT罗兰贝格品牌战略升级:华为案例启示与电器集团转型之路
罗兰贝格作为一家全球顶级的战略管理咨询公司,其品牌战略升级理念在多个行业中得到了广泛应用。以下将以华为案例为启示,探讨电器集团的转型之路,并融入罗兰贝格品牌战略升级的思想。 一、华为案例的启示 华为与罗兰贝格联合撰写的《数据存…...

系统设计,如何设计一个秒杀功能
需要解决的问题 瞬时流量的承接防止超卖预防黑产避免对正常服务的影响兜底方法 前端设计 利用 CDN 缓存静态资源,减轻服务器的压力在前端随机限流按钮防抖,防止用户重复点击 后端设计 Nginx 做统一接入,进行负载均衡与限流用 sentinel 等…...

Linux:进程入门(进程与程序的区别,进程的标识符,fork函数创建多进程)
往期文章:《Linux:深入了解冯诺依曼结构与操作系统》 Linux:深入理解冯诺依曼结构与操作系统-CSDN博客 目录 1. 概念 2. 描述进程 3. 深入理解进程的本质 4. 进程PID 4.1 指令获取PID 4.2 geipid函数获取PID 4.3 kill指令终止进程 …...

索尼MDR-M1:超宽频的音频盛宴,打造沉浸式音乐体验
在音乐的世界里,每一次技术的突破都意味着全新的听觉体验。 索尼,作为音频技术的先锋,再次以其最新力作——MDR-M1封闭式监听耳机,引领了音乐界的新潮流。 这款耳机以其超宽频播放和卓越的隔音性能,为音乐爱好者和专…...

【Linux】线程的概念
一、线程的概念 1.1 什么是线程 在一个程序里的一个执行路线就叫做线程,更准确的定义是:线程是“一个进程内部的控制序列”一切进程至少都有一个执行线程线程在进程内部运行,本质是在进程地址空间内运行在Linux系统中,在CPU眼中…...

centos7.9环境下mysql8数据库双机互备环境部署
为了实现mysql数据库的高可用性,数据库采用双机互备方式部署。双机互备能够避免单点故障造成的系统故障,由于两个节点都可以进行读写,同时也可以提高整个系统的数据读写并发性能。 1. 数据库安装 centos7安装mysql8 community 服务器IP:192.168.76.84 服务器IP:192.16…...

git 报错git: ‘remote-https‘ is not a git command. See ‘git --help‘.
报错内容 原因与解决方案 第一种情况:git路径错误 第一种很好解决,在环境变量中配置正确的git路径即可; 第二种情况 git缺少依赖 这个情况,网上提供了多种解决方案。但如果比较懒,可以直接把仓库地址的https改成ht…...
)
mysql学习教程,从入门到精通,SQL GROUP BY 子句(31)
1、SQL GROUP BY 子句 当然!在SQL中,GROUP BY 子句用于将结果集中的多个记录组合成一个摘要记录。通常,它用于结合聚合函数(如 COUNT(), SUM(), AVG(), MAX(), MIN() 等)来计算每个组的汇总信息。以下是一个详细的例子…...

pip 和 conda 的安装区别
在决定使用 pip 和 conda 安装包时,了解这两个包管理器之间的主要区别非常重要。以下是细分: 1. 区别 1.1. Package Management System 包裹管理系统 Pip: : Primarily used for Python packages. 主要用于 Python 包。 Installs package…...

大学生就业招聘:Spring Boot系统的架构分析
大学生就业招聘系统的设计与实现 摘要 随着信息互联网信息的飞速发展,大学生就业成为一个难题,好多公司都舍不得培养人才,只想要一专多能之人才,不愿是承担社会的责任,针对这个问题开发一个专门适应大学生就业招聘的网…...
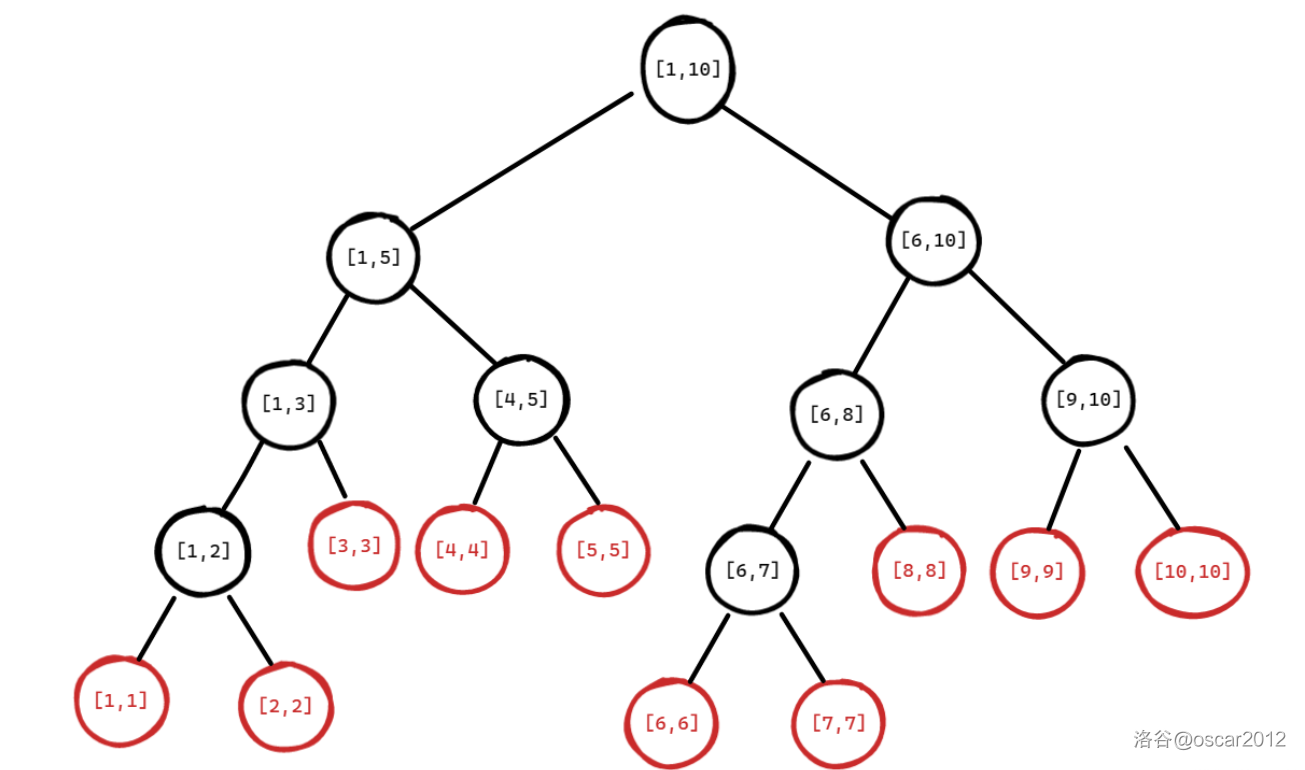
线段树模板
文章目录 线段树练习题目线段树概念区间维护辅助函数创建线段树 :build修改线段树 :modify查询线段树:query 全部代码 线段树 练习题目 洛谷题单 【模板】线段树 1 【模板】线段树 2 开关 扶苏的问题 线段树概念 线段树是一种高级数据结构&a…...

【TypeScript】知识点梳理(三)
#void前面提到了代表空,但有个特殊情况,是空不是空,细谈是取舍,但我们不深究hhh# 代码示例: type func () > voidconst f1: func function() {return true; } 定义了空,返回非空值,理论…...

题解:SP1741 TETRIS3D - Tetris 3D
这是一道二维线段树(树套树)标记永久化的模版题 前置知识点(来自董晓算法) 好,现在开始我们的分析: 题意简述: 在一个二维平面内,有给定的坐标,在这个坐标范围内加上…...

EWSTM8 IAR for STM8 软件分享
1. 软件简介 EWSTM8,即 IAR for STM8,全称为 IAR Embedded Workbench for STM8,它是 IAR ARM 嵌入式工作台之一,用于开发 STM8。IAR 有多个不同名的版本,对应不同的开发对象。 EWSTM8最新版本为V3.11(202…...

非机动车检测数据集 4类 5500张 电动三轮自行车 voc yolo
非机动车检测数据集 4类 5500张 电动三轮自行车 voc yolo 非机动车检测数据集介绍 数据集名称 非机动车检测数据集 (Non-Motorized Vehicle Detection Dataset) 数据集概述 该数据集专为训练和评估基于YOLO系列目标检测模型(包括YOLOv5、YOLOv6、YOLOv7等&#x…...

Chromium 中JavaScript FileReader API接口c++代码实现
FileReader 备注: 此特性在 Web Worker 中可用。 FileReader 接口允许 Web 应用程序异步读取存储在用户计算机上的文件(或原始数据缓冲区)的内容,使用 File 或 Blob 对象指定要读取的文件或数据。 文件对象可以从用户使用 <…...

k8s 中微服务之 MetailLB 搭配 ingress-nginx 实现七层负载
目录 1 MetailLB 搭建 1.1 MetalLB 的作用和原理 1.2 MetalLB功能 1.3 部署 MetalLB 1.3.1 创建deployment控制器和创建一个服务 1.3.2 下载MealLB清单文件 1.3.3 使用 docker 对镜像进行拉取 1.3.4 将镜像上传至私人仓库 1.3.5 将官方仓库地址修改为本地私人地址 1.3.6 运行清…...

南昌网站建设让你的企业网站更具竞争力
南昌网站建设让你的企业网站更具竞争力 在当今竞争激烈的市场环境中,一个高质量的网站不仅是企业形象的展示平台,更是吸引客户、提升业绩的重要工具。南昌作为江西的省会城市,互联网产业的蓬勃发展为企业网站建设提供了良好的机遇。 首先&am…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

