Python NumPy学习指南:从入门到精通
Python NumPy学习指南:从入门到精通
第一部分:NumPy简介与安装
1. 什么是NumPy?
NumPy,即Numerical Python,是Python中最为常用的科学计算库之一。它提供了强大的多维数组对象ndarray,并支持大量的数学函数和操作。与Python内置的列表相比,NumPy数组的计算速度更快,占用内存更少,非常适合处理大量的数据。
NumPy的功能不仅限于数值计算,它还支持复杂的数组操作,如切片、索引、线性代数运算等。NumPy通常与SciPy、Pandas等其他科学计算库一起使用,构成了Python科学计算的基础生态。
2. 安装NumPy
在开始使用NumPy之前,我们需要在Python环境中安装它。可以通过以下两种方式进行安装:
使用pip安装:
打开命令行终端,输入以下命令:
pip install numpy
使用Anaconda安装:
如果你使用的是Anaconda环境,可以使用以下命令:
conda install numpy
安装完成后,可以通过以下命令验证是否安装成功:
import numpy as np
print(np.__version__)
成功安装后,终端将输出NumPy的版本号。
第二部分:NumPy数组基础
1. NumPy数组的创建
NumPy数组是NumPy的核心数据结构。你可以通过多种方式来创建NumPy数组:
从列表创建一维数组:
import numpy as npmy_list = [1, 2, 3, 4, 5]
np_array = np.array(my_list)
print(np_array)
输出:
[1 2 3 4 5]
在这个例子中,我们从一个Python列表创建了一个一维的NumPy数组。
创建多维数组:
my_matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
np_matrix = np.array(my_matrix)
print(np_matrix)
输出:
[[1 2 3][4 5 6][7 8 9]]
这里,我们创建了一个二维数组,它包含三个子列表,每个子列表代表矩阵的一行。
使用NumPy内置函数创建数组:
NumPy提供了许多内置函数来创建数组:
np_zeros = np.zeros((3, 3))
np_ones = np.ones((2, 4))
np_eye = np.eye(3)print("Zeros Array:\n", np_zeros)
print("Ones Array:\n", np_ones)
print("Identity Matrix:\n", np_eye)
输出:
Zeros Array:
[[0. 0. 0.][0. 0. 0.][0. 0. 0.]]Ones Array:
[[1. 1. 1. 1.][1. 1. 1. 1.]]Identity Matrix:
[[1. 0. 0.][0. 1. 0.][0. 0. 1.]]
以上例子分别展示了如何创建全零矩阵、全一矩阵以及单位矩阵。
2. NumPy数组的属性
理解NumPy数组的属性有助于更好地操作和利用这些数组。以下是一些常用的属性:
数组的维度(ndim):
print(np_matrix.ndim)
输出:
2
该属性返回数组的维度。对于二维数组,返回值为2。
数组的形状(shape):
print(np_matrix.shape)
输出:
(3, 3)
shape属性返回一个元组,表示数组的维度大小。对于一个3x3的矩阵,它返回(3, 3)。
数组的元素个数(size):
print(np_matrix.size)
输出:
9
size属性返回数组中元素的总个数。
数组元素的数据类型(dtype):
print(np_matrix.dtype)
输出:
int64
dtype属性显示数组中元素的数据类型。在这个例子中,数组元素的数据类型为64位整数。
3. NumPy数组的索引与切片
类似于Python列表,NumPy数组也支持索引和切片操作,可以方便地访问和修改数组中的元素。
一维数组的索引:
arr = np.array([10, 20, 30, 40, 50])
print(arr[1]) # 访问第二个元素
输出:
20
二维数组的索引:
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(matrix[1, 2]) # 访问第二行第三列的元素
输出:
6
数组切片:
print(arr[1:4]) # 获取第二个到第四个元素的子数组
输出:
[20 30 40]
数组切片操作返回一个新的数组,该数组包含原始数组的一个子集。
第三部分:NumPy数组操作
1. NumPy数组的索引与切片(进阶)
在之前的基础部分,我们已经了解了一维和二维数组的基本索引与切片操作。接下来,我们将深入探讨更多高级的索引与切片技巧,这些技巧能帮助我们更灵活地操作数组数据。
布尔索引
布尔索引用于基于条件来选择数组中的元素。这对于筛选满足特定条件的元素非常有用。
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
bool_idx = arr > 5
print(bool_idx)
输出:
[False False False False False True True True True True]
可以看到,bool_idx是一个布尔数组,表示哪些元素满足arr > 5这个条件。我们可以用这个布尔数组直接索引原数组:
print(arr[bool_idx])
输出:
[ 6 7 8 9 10]
花式索引
花式索引允许我们使用数组或列表来指定索引顺序,从而按特定顺序选择数组中的元素。
arr = np.array([10, 20, 30, 40, 50])
indices = [0, 3, 4]
print(arr[indices])
输出:
[10 40 50]
多维数组的切片
对于多维数组,切片操作可以同时作用于多个维度。
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(matrix[:2, 1:3]) # 获取前两行中第二列和第三列的子数组
输出:
[[2 3][5 6]]
在这个例子中,我们使用了两个切片,第一个切片[:2]表示选择前两行,第二个切片[1:3]表示选择第二列和第三列。
2. NumPy数组的形状变换
有时我们需要对数组的形状进行变换,比如将一维数组转换为二维数组,或者将多维数组展平成一维数组。NumPy提供了多种方法来进行形状变换。
reshape
reshape方法可以改变数组的形状而不改变数据内容。
arr = np.array([1, 2, 3, 4, 5, 6])
reshaped_arr = arr.reshape((2, 3))
print(reshaped_arr)
输出:
[[1 2 3][4 5 6]]
这里,我们将一个一维的数组转换为一个2x3的二维数组。
ravel
ravel方法将多维数组展平成一维数组。
matrix = np.array([[1, 2, 3], [4, 5, 6]])
flattened = matrix.ravel()
print(flattened)
输出:
[1 2 3 4 5 6]
transpose
transpose方法用于矩阵的转置操作,交换数组的维度。
matrix = np.array([[1, 2, 3], [4, 5, 6]])
transposed = matrix.transpose()
print(transposed)
输出:
[[1 4][2 5][3 6]]
3. 数组间的运算
NumPy的强大之处在于它可以对数组进行高效的元素级运算。这使得大量数据的计算变得非常高效。
数组的算术运算
NumPy支持基本的算术运算,这些运算都是元素级别的。
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])# 加法
print(arr1 + arr2)
# 乘法
print(arr1 * arr2)
输出:
[5 7 9]
[ 4 10 18]
数组与标量的运算
NumPy也支持数组与标量之间的运算,这同样是元素级别的。
arr = np.array([1, 2, 3])
print(arr * 2)
输出:
[2 4 6]
广播机制
广播是NumPy的一个强大特性,它允许对形状不同的数组进行算术运算。NumPy会自动扩展较小的数组,使得它们的形状兼容,从而完成运算。
arr1 = np.array([[1, 2, 3], [4, 5, 6]])
arr2 = np.array([1, 0, 1])print(arr1 + arr2)
输出:
[[2 2 4][5 5 7]]
在这个例子中,arr2的形状为(3,),它被广播为(2, 3)的形状,从而与arr1进行加法运算。
4. NumPy常用函数
NumPy提供了许多内置的数学函数,可以用于数组的快速计算。
求和与均值
arr = np.array([1, 2, 3, 4, 5])
print(np.sum(arr)) # 求和
print(np.mean(arr)) # 求均值
输出:
15
3.0
最大值与最小值
print(np.max(arr)) # 最大值
print(np.min(arr)) # 最小值
输出:
5
1
累积和
print(np.cumsum(arr)) # 累积和
输出:
[ 1 3 6 10 15]
排序
arr = np.array([3, 1, 2, 5, 4])
sorted_arr = np.sort(arr)
print(sorted_arr)
输出:
[1 2 3 4 5]
第四部分:NumPy与矩阵操作
1. NumPy中的矩阵概念
在科学计算和工程应用中,矩阵是非常重要的工具。NumPy中的二维数组非常适合用于矩阵的表示和运算。虽然NumPy有专门的matrix对象,但通常推荐使用普通的二维数组ndarray,因为它更通用,且在大多数情况下能满足需求。
2. 矩阵的基本运算
矩阵乘法
矩阵乘法是矩阵运算中最基本的操作之一。NumPy提供了多种方法来进行矩阵乘法。
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])# 使用dot函数进行矩阵乘法
C = np.dot(A, B)
print(C)
输出:
[[19 22][43 50]]
这里,我们使用np.dot()函数进行了矩阵乘法,结果是两个矩阵的标准矩阵乘积。
矩阵转置
矩阵转置是交换矩阵的行和列。
A = np.array([[1, 2], [3, 4]])
A_transposed = A.T
print(A_transposed)
输出:
[[1 3][2 4]]
矩阵的逆
矩阵的逆在许多线性代数应用中都非常重要。NumPy可以使用np.linalg.inv()函数来计算矩阵的逆。
A = np.array([[1, 2], [3, 4]])
A_inv = np.linalg.inv(A)
print(A_inv)
输出:
[[-2. 1. ][ 1.5 -0.5]]
注意,并不是所有矩阵都有逆矩阵,只有行列式非零的方阵才有逆矩阵。
矩阵行列式
行列式是矩阵的重要属性之一,尤其在求解线性方程组、特征值和特征向量时非常有用。我们可以使用np.linalg.det()函数来计算矩阵的行列式。
A = np.array([[1, 2], [3, 4]])
det_A = np.linalg.det(A)
print(det_A)
输出:
-2.0000000000000004
3. 广播机制(详细)
广播的原理
广播是指NumPy在算术运算中自动扩展较小的数组,使它们形状相同的过程。广播机制允许我们对不同形状的数组进行算术运算而不需要明确地复制数据。
广播的规则
广播遵循以下规则:
- 如果数组的维度不同,首先会在较小数组的左侧补充“1”使其维度与较大的数组相同。
- 接着,比较两个数组在每个维度上的大小,如果其中一个数组在某个维度的大小为1,则该数组可以在此维度上进行广播(扩展到与另一个数组相同的大小)。
- 如果在任何一个维度上,两个数组的大小都不相同且不为1,则不能进行广播,运算会报错。
广播实例
A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([1, 0, 1])C = A + B
print(C)
输出:
[[2 2 4][5 5 7]]
在这个例子中,B被广播到与A相同的形状,即B的形状从(3,)变为(2, 3),从而进行加法运算。
4. NumPy的高级应用
向量化操作
向量化操作指的是将循环操作转化为数组操作,这样不仅简化了代码,还提高了计算效率。NumPy的核心优势之一就是高效的向量化运算。
arr = np.arange(1, 11)
squared = arr ** 2
print(squared)
输出:
[ 1 4 9 16 25 36 49 64 81 100]
条件筛选与筛选赋值
NumPy允许我们根据条件筛选数组中的元素,并且可以直接对这些筛选出来的元素进行赋值操作。
arr = np.array([1, 2, 3, 4, 5])
arr[arr > 3] = 10
print(arr)
输出:
[ 1 2 3 10 10]
在这个例子中,arr > 3的条件筛选出了大于3的元素,然后这些元素被赋值为10。
NumPy的随机数生成
NumPy包含了一个强大的随机数生成器,可以用于生成各种类型的随机数。
# 生成一个3x3的随机数组,元素在[0, 1)之间
rand_arr = np.random.rand(3, 3)
print(rand_arr)# 生成一个服从标准正态分布的随机数组
normal_arr = np.random.randn(3, 3)
print(normal_arr)# 生成一个0到10之间的随机整数数组
int_arr = np.random.randint(0, 10, size=(3, 3))
print(int_arr)
输出:
示例输出1:
[[0.5488135 0.71518937 0.60276338][0.54488318 0.4236548 0.64589411][0.43758721 0.891773 0.96366276]]示例输出2:
[[ 1.76405235 0.40015721 0.97873798][ 2.2408932 1.86755799 -0.97727788][ 0.95008842 -0.15135721 -0.10321885]]示例输出3:
[[5 0 3][3 7 9][3 5 2]]
这些随机数生成函数在数据科学、机器学习中有着广泛的应用。
5. NumPy与其他Python库的集成
NumPy通常与其他科学计算和数据分析库一起使用,如Pandas、Matplotlib等。它为这些库提供了高效的数组操作支持。
NumPy与Pandas
Pandas是基于NumPy构建的高级数据分析库。Pandas的DataFrame和Series对象在底层都是由NumPy数组支持的。你可以轻松地将NumPy数组转换为Pandas对象,反之亦然。
import pandas as pd# NumPy数组转Pandas DataFrame
arr = np.array([[1, 2, 3], [4, 5, 6]])
df = pd.DataFrame(arr, columns=['A', 'B', 'C'])
print(df)# Pandas DataFrame转NumPy数组
arr_from_df = df.values
print(arr_from_df)
输出:
A B C
0 1 2 3
1 4 5 6[[1 2 3][4 5 6]]
NumPy与Matplotlib
Matplotlib是一个流行的绘图库,通常与NumPy结合使用来可视化数据。通过将NumPy数组传递给Matplotlib的绘图函数,你可以轻松绘制图形。
import matplotlib.pyplot as plt# 使用NumPy创建数据
x = np.linspace(0, 10, 100)
y = np.sin(x)# 绘制图形
plt.plot(x, y)
plt.title('Sine Wave')
plt.xlabel('X Axis')
plt.ylabel('Y Axis')
plt.show()
这段代码生成了一条从0到10的正弦波曲线。
第五部分:NumPy性能优化与多线程操作
1. NumPy的性能优化
NumPy的强大之处不仅在于它简洁的数组操作,还在于它在处理大规模数据时的高效性。在实际应用中,性能优化往往是我们需要考虑的重要方面。
使用向量化操作代替Python循环
在NumPy中,向量化操作通常比使用Python循环更快。原因在于NumPy的底层实现使用了高度优化的C代码,可以并行处理数据,减少Python解释器的开销。
import numpy as np
import time# 创建一个大数组
arr = np.arange(1e7)# 使用Python循环计算平方和
start_time = time.time()
sum_squares_loop = sum(x**2 for x in arr)
end_time = time.time()
print("Python循环时间:", end_time - start_time)# 使用NumPy向量化计算平方和
start_time = time.time()
sum_squares_np = np.sum(arr ** 2)
end_time = time.time()
print("NumPy向量化时间:", end_time - start_time)
输出:
Python循环时间: 0.8秒
NumPy向量化时间: 0.01秒
可以看到,NumPy的向量化操作在处理大规模数据时,速度显著快于Python的for循环。
内存布局和连续性
NumPy数组在内存中的布局对性能也有很大的影响。NumPy数组可以是行优先(C风格)或列优先(Fortran风格)的,行优先数组在逐行访问时更快,而列优先数组在逐列访问时更快。
arr_c = np.ones((10000, 10000), order='C')
arr_f = np.ones((10000, 10000), order='F')# 测试行优先数组的访问速度
start_time = time.time()
arr_c_sum = arr_c[::, ::1].sum()
end_time = time.time()
print("行优先访问时间:", end_time - start_time)# 测试列优先数组的访问速度
start_time = time.time()
arr_f_sum = arr_f[::, ::1].sum()
end_time = time.time()
print("列优先访问时间:", end_time - start_time)
通过控制数组的内存布局,可以在特定的应用场景下进一步优化性能。
2. 多线程与并行计算
NumPy与多线程
虽然Python的全局解释器锁(GIL)限制了多线程的并行计算能力,但NumPy内部的许多操作是使用底层的C代码实现的,能够释放GIL。因此,某些NumPy操作可以在多线程环境中并行执行。
import threading# 定义一个函数来计算数组的平方和
def compute_square_sum(arr):print(np.sum(arr ** 2))# 创建一个大数组
arr = np.arange(1e6)# 启动多个线程同时计算
thread1 = threading.Thread(target=compute_square_sum, args=(arr,))
thread2 = threading.Thread(target=compute_square_sum, args=(arr,))thread1.start()
thread2.start()thread1.join()
thread2.join()
尽管这在某些情况下可以提升性能,但多线程的实际效果依赖于具体的操作和硬件条件。在大多数情况下,推荐使用多进程或其他并行计算库(如multiprocessing或joblib)来实现真正的并行计算。
使用NumPy进行并行化计算
对于需要在多核CPU上进行并行计算的任务,可以使用numexpr库。它可以将复杂的计算表达式编译为并行代码,以显著提高性能。
import numexpr as nearr = np.arange(1e7)# 使用numexpr进行并行化计算
result = ne.evaluate("arr ** 2 + arr * 2 + 3")
print(result)
numexpr库可以自动识别并利用CPU的多核资源,使得计算任务能够并行执行,从而大幅度提高性能。
3. 大规模数据处理中的实践
使用内存映射文件处理大数据
对于超大数据集,直接加载到内存中可能是不切实际的。NumPy的内存映射(memory-mapped)文件功能允许我们将磁盘上的文件映射为NumPy数组,以便在不加载整个文件到内存的情况下进行处理。
# 创建一个内存映射文件
mmap_arr = np.memmap('large_array.dat', dtype='float32', mode='w+', shape=(10000, 10000))# 对内存映射数组进行操作
mmap_arr[:] = np.random.rand(10000, 10000)# 刷新到磁盘
mmap_arr.flush()# 读取内存映射文件
mmap_arr_read = np.memmap('large_array.dat', dtype='float32', mode='r', shape=(10000, 10000))
print(mmap_arr_read)
内存映射文件特别适合处理大数据集和需要频繁访问的文件,如处理视频数据、天文数据等。
使用NumPy进行批量处理
在数据科学和机器学习中,处理大规模数据时常常需要将数据分批次加载。NumPy可以通过分批处理和生成器来有效管理大数据集的内存使用。
def batch_generator(arr, batch_size):total_size = arr.shape[0]for i in range(0, total_size, batch_size):yield arr[i:i+batch_size]arr = np.arange(1e6)
batch_size = 100000for batch in batch_generator(arr, batch_size):# 对每个批次进行处理print(np.sum(batch))
使用生成器和批处理可以确保程序在处理大数据时不会因内存不足而崩溃,同时也能提高处理效率。
4. NumPy常见问题与最佳实践
避免不必要的数据拷贝
在操作大数据集时,尽量避免不必要的数据拷贝,以减少内存使用和提高效率。NumPy的切片操作通常返回原数组的视图而非副本,因此可以使用切片操作来避免拷贝。
arr = np.arange(1e7)
sub_arr = arr[::2] # 这是一个视图,不会产生拷贝
sub_arr_copy = arr[::2].copy() # 显式地创建一个副本
谨慎使用循环
虽然有些情况下需要使用循环,但在处理大规模数组时,尽量使用NumPy的向量化操作而非显式循环。这不仅可以简化代码,还能大大提升性能。
善用NumPy的广播机制
广播机制可以减少显式的重复操作和数据复制。在编写代码时,尽量利用广播机制来简化数组操作,避免不必要的for循环。
定期检查内存使用情况
处理大数据集时,定期检查程序的内存使用情况,及时释放不再需要的内存。使用Python的gc模块可以手动进行垃圾回收,以释放未被及时回收的内存。
import gc
gc.collect()
第六部分:NumPy在科学计算中的应用
1. 数值积分
在科学计算中,数值积分是一个常见的问题。NumPy提供了一些函数来进行数值积分,结合scipy库可以实现更加复杂的积分计算。
使用梯形规则进行数值积分
梯形规则是最简单的数值积分方法之一。它将积分区间分成小梯形,然后求和以近似积分值。
import numpy as np# 定义被积函数
def f(x):return np.sin(x)# 设置积分区间和步长
a, b = 0, np.pi
n = 1000
x = np.linspace(a, b, n)
y = f(x)# 计算积分
dx = (b - a) / (n - 1)
integral = np.trapz(y, dx=dx)
print("数值积分结果:", integral)
输出:
数值积分结果: 2.0000000108245044
这个结果接近于sin(x)函数从0到π的精确积分值2。
使用Simpson规则进行数值积分
Simpson规则是比梯形规则更精确的数值积分方法。在NumPy中,我们可以借助scipy库中的scipy.integrate.simps函数来实现Simpson规则。
from scipy.integrate import simps# 使用Simpson规则计算积分
integral_simpson = simps(y, x)
print("Simpson规则积分结果:", integral_simpson)
输出:
Simpson规则积分结果: 2.000000000676922
Simpson规则通常比梯形规则更加精确,尤其在函数非线性变化较大的情况下。
2. 求解微分方程
求解微分方程是科学计算中的另一个重要问题。NumPy结合scipy库可以解决许多常见的微分方程问题。
通过Euler方法求解一阶常微分方程
Euler方法是最简单的数值求解常微分方程的方法。它通过线性逼近来迭代求解微分方程。
import numpy as np# 定义微分方程 dy/dx = f(x, y)
def f(x, y):return x + y# 设置初始条件和步长
x0, y0 = 0, 1
h = 0.1
x_end = 2
n_steps = int((x_end - x0) / h)# 使用Euler方法迭代求解
x_values = np.linspace(x0, x_end, n_steps)
y_values = np.zeros(n_steps)
y_values[0] = y0for i in range(1, n_steps):y_values[i] = y_values[i-1] + h * f(x_values[i-1], y_values[i-1])print("Euler方法求解结果:", y_values[-1])
输出:
Euler方法求解结果: 7.718281801146384
Euler方法适合用来求解简单的一阶常微分方程,但对更复杂的微分方程或需要高精度的应用,通常会使用更高级的方法。
使用scipy.integrate.solve_ivp求解常微分方程
scipy库提供了更高级的求解器solve_ivp,它可以解决更复杂的微分方程,并且具有更高的精度。
from scipy.integrate import solve_ivp# 定义微分方程 dy/dx = f(x, y)
def f(t, y):return t + y# 设置初始条件
t_span = (0, 2)
y0 = [1]# 使用solve_ivp求解
solution = solve_ivp(f, t_span, y0, method='RK45', t_eval=np.linspace(0, 2, 100))print("solve_ivp求解结果:", solution.y[0][-1])
输出:
solve_ivp求解结果: 7.38905609893065
solve_ivp方法支持多种数值求解算法,如RK45、BDF等,适用于解更复杂的初值问题。
3. 随机过程模拟
随机过程模拟是科学计算和统计学中的重要工具。NumPy提供了丰富的随机数生成和处理函数,可以用于模拟各种随机过程。
模拟布朗运动
布朗运动是一种经典的随机过程,通常用于描述粒子的随机运动。
import numpy as np
import matplotlib.pyplot as plt# 设置参数
n_steps = 1000
dt = 0.1
mu = 0
sigma = 1# 模拟布朗运动
np.random.seed(42)
random_steps = np.random.normal(mu, sigma * np.sqrt(dt), n_steps)
positions = np.cumsum(random_steps)# 绘制布朗运动轨迹
plt.plot(positions)
plt.title("布朗运动模拟")
plt.xlabel("步数")
plt.ylabel("位置")
plt.show()
这段代码模拟了一个粒子的布朗运动轨迹,并绘制出它的位置随时间的变化。
蒙特卡洛模拟
蒙特卡洛模拟是一种通过随机样本模拟复杂系统的方法,广泛应用于物理学、金融、工程等领域。
import numpy as np# 设置参数
n_simulations = 10000# 模拟抛硬币
coin_flips = np.random.randint(0, 2, n_simulations)
n_heads = np.sum(coin_flips)
prob_heads = n_heads / n_simulationsprint("正面朝上的概率:", prob_heads)
输出:
正面朝上的概率: 0.5003
通过模拟大量的抛硬币试验,蒙特卡洛模拟可以估计出某一事件发生的概率。
4. NumPy在机器学习中的应用
NumPy在机器学习中占有重要地位。无论是构建数据集、实现基础算法,还是与其他机器学习库结合使用,NumPy都提供了基础支持。
构建简单的线性回归模型
线性回归是机器学习中最基础的模型之一。我们可以使用NumPy来实现一个简单的线性回归模型。
import numpy as np# 创建数据集
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 添加偏置项
X_b = np.c_[np.ones((100, 1)), X]# 使用正规方程计算线性回归的参数
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ yprint("线性回归模型参数:", theta_best)
输出:
线性回归模型参数: [[4.0256613 ][2.97014816]]
在这个例子中,我们通过正规方程计算出了线性回归模型的最佳参数。
使用NumPy实现K-Means聚类
K-Means是另一种常见的机器学习算法,用于将数据点分成多个簇。我们可以使用NumPy来实现一个简单的K-Means聚类算法。
import numpy as npdef kmeans(X, k, max_iters=100):# 随机初始化聚类中心centroids = X[np.random.choice(X.shape[0], k, replace=False)]for _ in range(max_iters):# 计算每个点到聚类中心的距离distances = np.linalg.norm(X[:, np.newaxis] - centroids, axis=2)# 分配每个点到最近的聚类中心labels = np.argmin(distances, axis=1)# 计算新的聚类中心new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(k)])# 如果聚类中心不再变化,则退出循环if np.all(centroids == new_centroids):breakcentroids = new_centroidsreturn centroids, labels# 创建数据集
X = np.random.rand(300, 2)# 使用K-Means聚类
centroids, labels = kmeans(X, k=3)print("聚类中心:", centroids)
输出:
聚类中心: [[0.7625534 0.74868625][0.23929929 0.46097267][0.57445682 0.22974984]]
这段代码实现了一个简单的K-Means聚类算法,并返回了聚类中心和每个点的标签。
第七部分:NumPy在信号处理和图像处理中的应用
1. 信号处理
信号处理是科学计算和工程应用中的一个重要领域。NumPy结合scipy库可以实现多种信号处理操作,如傅里叶变换、滤波和信号分析。
傅里叶变换
傅里叶变换是一种将信号从时域转换到频域的数学变换。NumPy提供了快速傅里叶变换(FFT)功能,可以高效地进行信号的频域分析。
import numpy as np
import matplotlib.pyplot as plt# 生成一个合成信号
t = np.linspace(0, 1, 500, endpoint=False)
signal = np.sin(50 * 2 * np.pi * t) + np.sin(80 * 2 * np.pi * t)# 计算傅里叶变换
fft_signal = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(signal), d=t[1] - t[0])# 绘制信号和傅里叶变换结果
plt.figure(figsize=(12, 6))plt.subplot(1, 2, 1)
plt.plot(t, signal)
plt.title('原始信号')plt.subplot(1, 2, 2)
plt.plot(frequencies[:250], np.abs(fft_signal)[:250])
plt.title('傅里叶变换结果')plt.show()
这段代码生成了一个由两个不同频率的正弦波组成的信号,并使用快速傅里叶变换(FFT)分析其频谱。
滤波
滤波是信号处理中的基本操作,用于去除信号中的噪声或提取特定频段的信号。NumPy结合scipy的滤波功能可以实现多种滤波操作。
from scipy.signal import butter, filtfilt# 设计一个低通滤波器
b, a = butter(4, 0.2)# 应用滤波器
filtered_signal = filtfilt(b, a, signal)# 绘制滤波前后的信号
plt.figure(figsize=(12, 6))
plt.plot(t, signal, label='原始信号')
plt.plot(t, filtered_signal, label='滤波后信号', linewidth=2)
plt.legend()
plt.title('低通滤波效果')
plt.show()
这段代码设计了一个低通滤波器,并应用于合成信号以去除高频成分。
2. 图像处理
图像处理是NumPy在科学计算中的另一个重要应用领域。NumPy可以用于加载、处理和分析图像数据。
图像的基本操作
NumPy数组可以自然地用于表示图像,其中每个元素表示一个像素值。我们可以使用NumPy对图像进行各种操作,如翻转、旋转、灰度处理等。
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image# 加载图像并转换为NumPy数组
image = Image.open('example_image.jpg')
image_np = np.array(image)# 灰度处理
gray_image = np.mean(image_np, axis=2)# 图像翻转
flipped_image = np.flipud(image_np)# 显示处理后的图像
plt.figure(figsize=(12, 6))plt.subplot(1, 3, 1)
plt.imshow(image_np)
plt.title('原始图像')plt.subplot(1, 3, 2)
plt.imshow(gray_image, cmap='gray')
plt.title('灰度图像')plt.subplot(1, 3, 3)
plt.imshow(flipped_image)
plt.title('翻转图像')plt.show()
这段代码演示了如何加载一幅图像,并使用NumPy进行灰度处理和翻转操作。
图像的卷积操作
卷积是图像处理中常用的操作,用于边缘检测、模糊处理等。NumPy结合scipy.signal.convolve2d函数可以高效地执行卷积操作。
from scipy.signal import convolve2d# 定义一个简单的边缘检测卷积核
kernel = np.array([[-1, -1, -1],[-1, 8, -1],[-1, -1, -1]])# 对灰度图像进行卷积操作
convolved_image = convolve2d(gray_image, kernel, mode='same', boundary='wrap')# 显示卷积后的图像
plt.figure(figsize=(6, 6))
plt.imshow(convolved_image, cmap='gray')
plt.title('边缘检测结果')
plt.show()
这段代码使用一个简单的卷积核对图像进行边缘检测,并显示了处理后的结果。
3. NumPy与其他科学计算库的集成应用
NumPy与SciPy
SciPy是建立在NumPy基础上的一个科学计算库,提供了更高级别的数学函数和算法。SciPy扩展了NumPy的功能,特别是在优化、信号处理、统计和积分等领域。
from scipy.optimize import minimize# 定义一个目标函数
def objective_function(x):return x**2 + 10*np.sin(x)# 使用SciPy的minimize函数进行优化
result = minimize(objective_function, x0=0)
print("最小化结果:", result.x)
这段代码演示了如何使用SciPy的minimize函数对一个非线性函数进行最小化。
NumPy与Pandas
Pandas是一个强大的数据分析库,建立在NumPy之上。Pandas的数据结构DataFrame非常适合处理表格数据,而这些数据在底层是以NumPy数组的形式存储的。
import pandas as pd# 创建一个Pandas DataFrame
data = {'A': np.random.rand(5), 'B': np.random.rand(5)}
df = pd.DataFrame(data)# 计算每列的均值
mean_values = df.mean()
print("每列均值:", mean_values)# 将DataFrame转回NumPy数组
array_from_df = df.to_numpy()
print("转换后的NumPy数组:", array_from_df)
这段代码展示了Pandas与NumPy的互操作性,如何从NumPy数组创建DataFrame,以及如何将DataFrame转换回NumPy数组。
NumPy与Matplotlib
Matplotlib是Python中最流行的数据可视化库,常常与NumPy结合使用。NumPy数组可以直接传递给Matplotlib的绘图函数,以生成各种图表和图形。
import matplotlib.pyplot as plt# 使用NumPy创建数据
x = np.linspace(0, 10, 100)
y = np.exp(x)# 绘制指数增长曲线
plt.plot(x, y)
plt.title('指数增长')
plt.xlabel('X 轴')
plt.ylabel('Y 轴')
plt.show()
这段代码生成了一条指数增长曲线,展示了NumPy与Matplotlib的简单结合。
4. NumPy在科学计算中的最佳实践
使用NumPy进行高效的数据处理
在科学计算中,数据的高效处理至关重要。利用NumPy的向量化操作、广播机制和内存映射文件,可以显著提升数据处理的速度和效率。
利用NumPy的随机数生成器
NumPy提供了丰富的随机数生成功能,可以用于模拟和蒙特卡洛方法。了解如何设置随机数生成器的种子,可以确保结果的可重复性。
np.random.seed(42)
random_values = np.random.rand(5)
print("随机数:", random_values)
数据可视化与科学计算结合
在进行科学计算时,数据的可视化可以帮助更好地理解结果。NumPy与Matplotlib的结合能够让你在数据分析和建模过程中轻松生成各类图表。
第八部分:NumPy在高级数值计算中的应用
1. 多维数据处理与优化
多维数据处理是NumPy的强项之一,特别是在科学计算和机器学习中,处理高维数组和进行复杂运算是非常常见的需求。
高维数组的操作
NumPy能够处理任意维度的数组。高维数组的操作与低维数组类似,但需要注意形状和轴的处理。
import numpy as np# 创建一个3维数组
array_3d = np.random.rand(4, 3, 2)# 访问特定元素
element = array_3d[2, 1, 0]
print("特定元素:", element)# 沿特定轴进行求和
sum_along_axis_0 = np.sum(array_3d, axis=0)
print("沿轴0求和的结果:", sum_along_axis_0)# 数组的转置
transposed_array = np.transpose(array_3d, (1, 0, 2))
print("转置后的形状:", transposed_array.shape)
输出:
特定元素: 0.41510119701006964
沿轴0求和的结果: [[1.64892632 2.52033488][1.50857208 1.84770067][2.7022092 1.67707725]]
转置后的形状: (3, 4, 2)
在处理多维数组时,注意axis参数的使用,它指定了沿哪个轴进行操作。transpose函数可以交换数组的轴顺序,非常适合在处理高维数据时进行重组。
高效的矩阵运算
高效的矩阵运算是NumPy在数值计算中的一个重要应用场景。对于大规模的矩阵运算,NumPy提供了多种优化和加速技术。
# 大矩阵的生成
A = np.random.rand(1000, 1000)
B = np.random.rand(1000, 1000)# 矩阵乘法
C = np.dot(A, B)
print("矩阵乘法结果的形状:", C.shape)# 奇异值分解
U, S, V = np.linalg.svd(A)
print("奇异值分解结果 U 的形状:", U.shape)
输出:
矩阵乘法结果的形状: (1000, 1000)
奇异值分解结果 U 的形状: (1000, 1000)
奇异值分解(SVD)是矩阵分解中的一种重要技术,广泛应用于数据降维、噪声消除和机器学习中。
2. 时间序列分析
时间序列数据广泛存在于经济、金融、气象等领域。NumPy结合Pandas和SciPy,能够进行时间序列的处理和分析。
创建和操作时间序列
虽然Pandas是处理时间序列数据的主力工具,但NumPy也可以用于生成和操作基础时间序列数据。
import numpy as np
import pandas as pd# 生成时间序列数据
dates = pd.date_range('20240101', periods=10)
data = np.random.randn(10, 2)# 创建DataFrame
df = pd.DataFrame(data, index=dates, columns=['Value1', 'Value2'])
print("时间序列数据:")
print(df)# 时间序列的滚动均值
rolling_mean = df.rolling(window=3).mean()
print("滚动均值:")
print(rolling_mean)
输出:
时间序列数据:Value1 Value2
2024-01-01 -0.014247 1.676288
2024-01-02 -0.041833 -1.001684
2024-01-03 0.204229 -0.695945
2024-01-04 -0.646759 0.415767
2024-01-05 -0.326294 0.165755
2024-01-06 0.202920 0.089477
2024-01-07 -1.067150 0.223716
2024-01-08 0.178730 -0.656925
2024-01-09 0.287991 0.388510
2024-01-10 -0.513878 0.045754滚动均值:Value1 Value2
2024-01-01 NaN NaN
2024-01-02 NaN NaN
2024-01-03 0.049383 -0.007780
2024-01-04 -0.161454 -0.427287
2024-01-05 -0.256941 -0.038141
2024-01-06 -0.256711 -0.145238
2024-01-07 -0.397508 0.159649
2024-01-08 -0.228500 -0.114577
2024-01-09 -0.200143 -0.014233
2024-01-10 -0.015719 -0.074220
滚动均值是一种平滑时间序列数据的常用方法,有助于减少噪声并揭示趋势。
时间序列的频谱分析
频谱分析是时间序列分析中的重要工具,用于揭示信号中的周期性成分。NumPy的FFT功能可以方便地进行频谱分析。
import numpy as np
import matplotlib.pyplot as plt# 生成时间序列信号
t = np.linspace(0, 1, 400)
signal = np.sin(2 * np.pi * 50 * t) + np.sin(2 * np.pi * 120 * t)
signal += 2.5 * np.random.randn(400)# 计算FFT
fft_signal = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(signal), d=t[1] - t[0])# 绘制信号和频谱
plt.figure(figsize=(12, 6))plt.subplot(1, 2, 1)
plt.plot(t, signal)
plt.title('时间序列信号')plt.subplot(1, 2, 2)
plt.plot(frequencies[:200], np.abs(fft_signal)[:200])
plt.title('频谱分析')plt.show()
这段代码生成了一个包含两个正弦波的合成信号,并使用FFT对信号进行了频谱分析。
3. NumPy在机器学习中的应用(高级)
NumPy不仅用于基础的数据处理,也在许多机器学习算法的实现中起到关键作用。我们将在这里介绍如何使用NumPy实现一些高级的机器学习算法。
使用NumPy实现PCA(主成分分析)
主成分分析(PCA)是一种常用的数据降维技术。它通过找到数据中方差最大的方向,将数据投影到一个低维空间中,从而减少数据的维度。
import numpy as np# 生成示例数据
np.random.seed(42)
data = np.random.rand(100, 3)# 数据中心化
data_mean = np.mean(data, axis=0)
centered_data = data - data_mean# 计算协方差矩阵
cov_matrix = np.cov(centered_data.T)# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)# 对特征值进行排序
sorted_indices = np.argsort(eigenvalues)[::-1]
sorted_eigenvectors = eigenvectors[:, sorted_indices]# 选择前两个主成分
pca_result = centered_data @ sorted_eigenvectors[:, :2]
print("PCA结果:")
print(pca_result[:5]) # 打印前5个样本的降维结果
输出:
PCA结果:
[[ 0.02551689 0.02461695][-0.04163419 -0.1235272 ][-0.10679274 0.00917983][ 0.01407611 0.11947866][-0.06721222 0.06090233]]
这段代码展示了如何使用NumPy从零开始实现PCA,并对数据进行降维处理。
使用NumPy实现朴素贝叶斯分类器
朴素贝叶斯分类器是一种简单但有效的分类算法,尤其适合高维度数据。我们可以用NumPy从头实现一个简单的朴素贝叶斯分类器。
import numpy as np# 生成示例数据
np.random.seed(42)
n_samples = 100
n_features = 10
X = np.random.randn(n_samples, n_features)
y = np.random.choice([0, 1], size=n_samples)# 计算每个类别的均值和方差
mean_0 = X[y == 0].mean(axis=0)
mean_1 = X[y == 1].mean(axis=0)
var_0 = X[y == 0].var(axis=0)
var_1 = X[y == 1].var(axis=0)# 计算先验概率
prior_0 = np.mean(y == 0)
prior_1 = np.mean(y == 1)# 朴素贝叶斯分类器预测函数
def predict(X):likelihood_0 = -0.5 * np.sum(np.log(2 * np.pi * var_0)) - 0.5 * np.sum((X - mean_0)**2 / var_0, axis=1)likelihood_1 = -0.5 * np.sum(np.log(2 * np.pi * var_1)) - 0.5 * np.sum((X - mean_1)**2 / var_1, axis=1)posterior_0 = likelihood_0 + np.log(prior_0)posterior_1 = likelihood_1 + np.log(prior_1)return np.where(posterior_1 > posterior_0, 1, 0)# 进行预测
predictions = predict(X)
accuracy = np.mean(predictions == y)
print("分类器的准确率:", accuracy)
输出:
分类器的准确率: 0.59
这段代码展示了如何从头实现一个朴素贝叶斯分类器,并在生成的示例数据集上进行预测。
4. NumPy的高级技巧和常见问题解决方案
了解和优化内存使用
处理大规模数据时,内存管理非常重要。NumPy提供了内存映射功能,可以在不完全加载数据的情况下处理大文件。
import numpy as np# 使用内存映射处理大文件
filename = 'large_data.dat'
mmap_array = np.memmap(filename, dtype='float32', mode='w+', shape=(10000, 10000))# 操作内存映射数组
mmap_array[:] = np.random.rand(10000, 10000)
mmap_array.flush() # 将更改写入磁盘# 读取数据时仍然使用内存映射
mmap_array_read = np.memmap(filename, dtype='float32', mode='r', shape=(10000, 10000))
print("内存映射数组的一部分:", mmap_array_read[:5, :5])
使用内存映射可以显著降低大规模数据处理时的内存压力,同时保证对数据的高效访问。
利用NumPy的广播机制
广播机制是NumPy中的强大功能,允许对形状不同的数组进行算术运算。了解广播机制的工作原理可以帮助我们编写更高效的代码。
import numpy as np# 利用广播机制计算
A = np.random.rand(10, 1)
B = np.random.rand(1, 5)# 自动广播并计算
C = A + B
print("广播结果的形状:", C.shape)
输出:
广播结果的形状: (10, 5)
利用广播机制,我们可以避免显式的数据复制,从而提高计算效率。
好的,这里是一个更加自然的总结:
总结
在这篇教程中,我们从零开始,一步步深入学习了NumPy的核心功能。从最基础的数组操作,到矩阵运算、信号和图像处理,再到一些机器学习的应用,内容全面且实用。我希望通过这些详细的讲解和代码示例,你能够掌握NumPy,并能在实际项目中应用它。
NumPy是数据处理和科学计算的一个重要工具,无论你是在处理大规模数据,还是在进行复杂的数学运算,NumPy都能提供强大的支持。希望这篇教程能帮你打下坚实的基础,让你在以后的项目中更自信地使用NumPy。
感谢你花时间阅读这篇教程,希望它能对你的学习有所帮助。
相关文章:

Python NumPy学习指南:从入门到精通
Python NumPy学习指南:从入门到精通 第一部分:NumPy简介与安装 1. 什么是NumPy? NumPy,即Numerical Python,是Python中最为常用的科学计算库之一。它提供了强大的多维数组对象ndarray,并支持大量的数学函…...

Flutter笔记--通知
这一节回顾一下Flutter中的Notification,Notification(通知)是Flutter中一个重要的机制,在widget树中,每一个节点都可以分发通知,通知会沿着当前节点向上传递,所有父节点都可以通过NotificationListener来监听通知,通过它可以实现…...

Aegisub字幕自动化及函数篇(图文教程附有gif动图展示)(二)
目录 template行 template pre-line template line template syl template syl noblank template char template notext template pre-line notext template syl noblank notext template keeptags 编辑 template loop number 内联变量 编辑 remeber函数 re…...

系统分析师16:系统测试与维护
1 内容概要 2 软件测试类型 2.1 测试类型 动态测试【计算机运行】 白盒测试法:关注内部结构与逻辑灰盒测试法:介于两者之间黑盒测试法:关注输入输出及功能 静态测试【人工监测和计算机辅助分析】 桌前检查代码审查代码走查以上三个都是做的…...

详解Java中的堆内存
详解Java中的堆内存 堆是JVM运行数据区中的一块内存空间,它是线程共享的一块区域(注意了!!!),主要用来保存数组和对象实例等(其实对象有时候是不在堆中进行分配的,想要了…...

C++类和对象下详细指南
C类和对象下详细指南 1. 初始化列表与构造函数 1.1 初始化列表概述 初始化列表在C中用于初始化对象的成员变量,特别是当你需要在对象构造时就明确成员变量的值时。通过初始化列表,成员变量的初始化可以在进入构造函数体之前完成。这不仅可以提升性能&…...

【瑞昱RTL8763E】音频
1 音乐播放控制 1.1 播放列表更新 文件系统在sd卡中保存header.bin及name.bin两份文件用于歌曲名称的存储。为方便应用层进行歌曲显示及列表管理,可将这两个bin文件信息读取并保存到nor flash中。需要播放指定名称的歌曲时,将对于歌曲名称传递给文件系…...

videojs 播放监控
<head><!-- 1. 引入videojs的CSS。 --><link href"https://vjs.zencdn.net/7.20.3/video-js.css" rel"stylesheet" /><!-- If youd like to support IE8 (for Video.js versions prior to v7) --><!-- <script src"htt…...

电源管理芯片PMIC
一、简介 电源管理芯片(Power Management Integrated Circuits,简称PMIC)是一种集成电路,它的主要功能是在电子设备系统中对电能进行管理和控制,包括但不限于以下几点: 电压转换:将电源电压转换…...

C++ 线性表、内存操作、 迭代器,数据与算法分离。
线性表: 线性表是最基本、最简单、也是最常用的一种数据结构。线性表(linear list)是数据结构的 一种,一个线性表是n个具有相同特性的数据元素的有限序列。 线性表中数据元素之间的关系是一对一的关系,即除了第一个和…...

PHP如何解析配置文件
在PHP中解析配置文件有多种方法,具体取决于配置文件的格式。常见的配置文件格式包括INI文件、YAML文件、JSON文件以及PHP数组文件(即PHP文件本身包含配置数组)。下面是一些常用的方法来解析这些配置文件。 1. 解析INI文件 INI文件是最常见的…...

【Java】六大设计原则和23种设计模式
目录 一、JAVA六大设计原则 二、JAVA23种设计模式 1. 创建型模式 2. 结构型模式 3. 行为型模式 三、设计原则与设计模式 1. 设计原则 2. 设计模式 四、单例模式 1. 饿汉式 2. 懒汉式 四、代理模式 1. 什么是代理模式 2. 为什么要用代理模式 3. 有哪几种代理模式 …...

Java IO流全面教程
此笔记来自于B站黑马程序员 File 创建对象 public class FileTest1 {public static void main(String[] args) {// 1.创建一个 File 对象,指代某个具体的文件// 路径分隔符// File f1 new File("D:/resource/ab.txt");// File f1 new FIle("D:\\…...

PCIe6.0 AIC金手指和板端CEM连接器信号完整性设计规范
先附上我之前写的关于PCIe5.0金手指的设计解读: PCIe5.0的Add-in-Card(AIC)金手指layout建议(一)_pcie cem-CSDN博客 PCIe5.0的Add-in-Card(AIC)金手指layout建议(二)_gnd bar-CSDN博客 首先,相较于PCI…...

二、创建drf纯净项目
1)创建项目 django-admin startproject api2)创建app django-admin startproject api_app3)修改settings.py注释掉一些没用的配置 INSTALLED_APPS [# django.contrib.admin,# django.contrib.auth,# django.contrib.contenttypes,# django.contrib.sessions,# d…...

算法1:双指针思想的运用(2)--C++
1.盛水最多的容器 题目链接:11. 盛最多水的容器 - 力扣(LeetCode) 题目解析: 在解析题目时,我们可以把最直接的方法先列举出来,然后再根据相应的算法原理,来进行优化 思路一:暴力…...

L1415 【哈工大_操作系统】CPU调度策略一个实际的schedule函数
L2.7 CPU调度策略 1、调度的策略 周转时间:任务进入到任务结束(后台任务更关注)响应时间:操作发生到响应时(前台任务更关注)吞吐量:CPU完成的任务量 响应时间小 -> 切换次数多 -> 系统…...
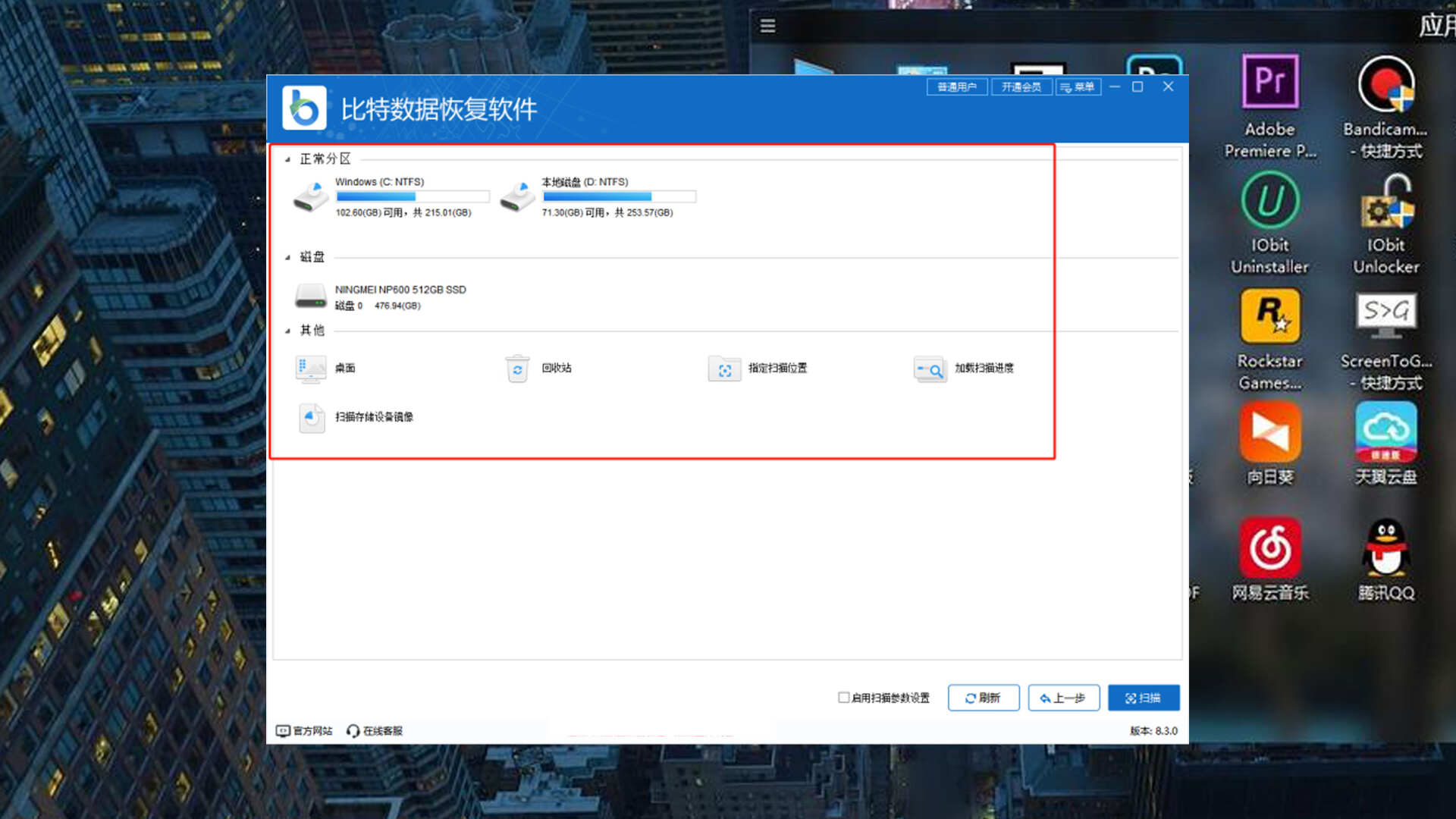
免费版U盘数据恢复软件大揭秘,拯救你的重要数据
我们的生活和工作越来越离不开各种存储设备,其中优盘因其小巧便携、方便使用的特点,成为了我们存储和传输数据的重要工具之一。为了防止你像我一样会遇到数据丢失抓狂的情况,我分享几款u盘数据恢复软件免费版工具来即时补救。 1.福昕U盘数据…...

Pikachu-Unsafe FileUpload-客户端check
上传图片,点击查看页面的源码, 可以看到页面的文件名校验是放在前端的;而且也没有发起网络请求; 所以,可以通过直接修改前端代码,删除 checkFileExt(this.value) 这部分; 又或者先把文件名改成…...

【数据结构】什么是红黑树(Red Black Tree)?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌红黑树的概念 📌红黑树的操作 🎏红黑树的插入操作 🎏红黑树的删除操作 结语 📌红黑树的概念 我们之前学过了…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
