【数据结构】什么是红黑树(Red Black Tree)?
🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

目录
📌红黑树的概念
📌红黑树的操作
🎏红黑树的插入操作
🎏红黑树的删除操作
结语
📌红黑树的概念
我们之前学过了二叉搜索树和平衡二叉搜索(AVL)树, 除了它们, 还有一个被广泛运用的平衡二叉搜索树是红黑树(RB-Tree)。
红黑树是一种平衡二叉搜索树的变体, 它的左右子树高差有可能大于 1,所以红黑树不是严格意义上的平衡二叉搜索树(AVL),但对之进行平衡的代价较低, 其平均统计性能要强于 AVL 。
红黑树在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
红黑树的规则如下:
- 每个结点不是红色就是黑色
- 根结点是黑色
- 如果一个结点是红色的,则它的子结点一定是黑色
- 任一结点到NULL(树尾)的任何路径上,所含的黑色结点数一定相同
- 每个NULL(树尾)空结点都是黑色的
依照红黑树的规则,红黑树能确保没有一条路径会比其他路径长出俩倍的原因是:
因此假设所有路径的黑节点数是n,那么最短路径的长度为n,而最长路径的长度为2n-1.
红黑树和AVL树的效率差异:
因为AVL树是较严格的平衡二叉搜索树,因此当数据量为n时,它的查询效率最坏大概在
。而对于红黑树来讲,假设它的最短路径层高和AVL树的层高一样,那它的最坏查询效率大概就在
。虽然略逊AVL树,但两者的效率仍然处于一个量级,即使有10亿数据,AVL树的查询次数在30次左右,而红黑树的查询次数在60次左右,差距不是很大,但是在插入时红黑树对于AVL树的消耗却少了不少,因此STL库中set和map的底层都是通过封装红黑树实现的.
📌红黑树的操作
🎏红黑树的插入操作
我们同样以一组数据为例, 在模拟红黑树插入的过程中学习红黑树对于插入结点的处理方法。
在此之前,我们需要先搞清楚一个问题, 那就是每个结点都有颜色,或红色或黑色,那么新插入的结点应该是红色还是黑色呢?答案是, 必须是红色!
我们简单分析一下插入新结点的情况, 假设我们现在需要给下面这颗红黑树中插入一个新结点7:
我们先来看看如果这个结点为黑节点的情况:
给大家举一个例子, 想来大家或多或少都有听说过或者经历过被人催婚的经历, 有一个很有趣的现象, 不知道大家有没有观察到, 那就是催婚的力度, 和年龄的关系不是很大,但是和同辈人有没有结婚生子关系非常大,也就是说,当家里亲戚里同辈人都没有结婚生子时,催婚的力度可能就是"天街小雨润如酥"。但是一旦同辈人中有人已经结婚生子了,那催婚的力度可就是"涧底松摇千尺雨"了。
上图中新插入黑节点的行为就像是第一个结婚生子的同辈人,明明同辈人大家一起在坚守战线, 但是他却叛变了, 这下剩下所有的结点的平衡都因为它而打破, 破坏力简直是毁灭级的, 所以我们新插入的结点一定不能是黑色的。
那假如我们插入的新节点是红结点呢?
我们可以看到,如果插入的红结点父亲是黑节点,那么红结点的插入就不会破坏任何红黑树的规则, 这就相当于同辈人没有直接结婚生子,而只是谈了一个男/女朋友,并不会真正影响到平衡的格局, 只是偶尔会遇到父节点也是红结点的情况,这个时候我们按后面学到的处理方法将他们处理一下就可以.
如果我们遇到了插入后违反红黑树规则的情况,那么红黑树的调整规则如下:
- 插入结点是根节点(即破坏了根节点是黑色的规则)--->解决方法,直接将该节点变黑
- 插入结点的父节点也是红色(即破坏了红结点的孩子必须是黑色的规则),分两种情况
- 插入结点的叔叔结点是红色: 将叔叔和父亲变为黑色, 爷爷结点变为红色, 然后继续向上判定爷爷结点是否违反了红黑树的规则并进行调整
- 插入结点的叔叔结点不存在或是黑色: 根据形态进行相应的旋转操作,旋转完成后,将旋转后的根节点变黑,将祖父结点变红即可
接下来我们就一起按照这组数据来模拟红黑树的插入过程:
17 18 23 34 27 15 9 6 8 5 25
首先插入第一个结点17:
可以看到,插入根节点时,我们违反了根结点为黑的性质,解决办法也很简单,把根节点变黑就行:
继续插入下一个结点18:
插入后没有破坏红黑树的任何性质,继续插入
插入下一个结点23:
此时违反了红黑树不能有两个连续红结点的性质,并且对新插入的结点23来讲,它的叔叔结点不存在,因此我们考虑使用旋转来解决,观察发现此时是RR型的旋转,因此我们通过左旋来解决:
左旋之后,我们需要将新的父亲结点变为黑色,原来的爷爷结点变为红色就完成了:
继续插入下一个结点34:
此时违反了红黑树不能有两个连续红结点的性质,并且对新插入的结点34来讲,它的叔叔结点是红色的,因此我们需要对将父亲叔叔变为黑色,爷爷变为红色:
然后继续将爷爷结点18作为新插入结点继续向上判定,发现他不符合根结点是黑色结点的性质,因此我们将根节点18变为黑色即可:
向上判定到了根节点就结束了, 我们继续插入下一个结点.
继续插入下一个结点27:
发现此时新插入结点27和它的父亲结点34违反了不能有两个相同红结点的规则,通过观察,我们发现他没有叔叔结点, 又因为是RL型,因此我们选择右左双旋来解决这个问题:
旋转好后,再对旋转后的根节点27和祖父结点23进行变色:
变色完成,我们的红黑树也就插入成功了.
继续插入下一个结点15:
发现并没有破坏红黑树的任何性质, 继续插入下一个结点.
继续插入下一个结点9:
发现新插入的9和其父亲结点15违反了不能有两个连续红结点的性质,同时其叔叔结点也不存在,通过观察是LL型旋转,因此我们选择右旋来解决这个问题:
右旋完成后,我们更改旋转后的根节点15和爷爷结点17进行变色,就调整好了:
继续插入下一个结点6:
发现新插入的6和其父亲结点9违反了不能有两个连续红结点的性质,同时其叔叔是红色,因此我们选择将父亲结点叔叔结点和爷爷结点变色来解决这个问题:
变色完成后,我们继续判断爷爷结点是否有违反红黑树的性质,发现没有,插入完成.
继续插入下一个结点8:
发现新插入的8和其父亲结点6违反了不能有两个连续红结点的性质,同时其叔叔结点也不存在,通过观察是LR型旋转,因此我们选择左右双旋来解决这个问题:
旋转完成后,我们再对旋转后的根节点8,和爷爷结点9进行变色, 既可完成插入:
继续插入下一个结点5:
发现新插入的5和其父亲结点6违反了不能有两个连续红结点的性质,同时其叔叔是红色,因此我们选择将父亲结点叔叔结点和爷爷结点变色来解决这个问题:
变色完成后,我们继续判断爷爷结点8是否有违反红黑树的性质,发现结点8和其父亲结点15违反了不能有两个连续红结点的性质,同时其叔叔结点27是黑色,通过观察是LL型旋转,因此我们选择右旋来解决这个问题:
右旋完成后,我们更改旋转后的根节点15和爷爷结点18进行变色,就调整好了:
继续插入最后一个结点25:
发现新插入的25和其父亲结点23违反了不能有两个连续红结点的性质,同时其叔叔34是红色,因此我们选择将父亲结点叔叔结点和爷爷结点变色来解决这个问题:
变色之后,继续判断爷爷结点27是否违反红黑树性质,发现结点27和它的父亲结点18违反了不能有两个连续红结点的性质,同时其叔叔结点8是红色,因此我们选择将父亲结点18叔叔结点8和爷爷结点15变色来解决这个问题:
变色之后,继续判断新的爷爷结点15是否违反红黑树性质,发现他违反了根节点必须为黑的性质,因此我们将他变黑,又因为已经判断到根节点, 插入操作完成.
将所有元素插入进红黑树后,我们显示出所有的空结点,验证红黑树的性质,发现是符合红黑树的性质的:
🎏红黑树的删除操作
红黑树和AVL树一样,都是要在二叉搜索树的删除插入基础上然后保持其树本身的特性.
红黑树的删除难点主要在于删除叶子黑节点。
因为有孩子结点时我们只需要按二叉搜索树的逻辑让孩子结点代替它,并让孩子结点变黑即可。
对于叶子红结点呢,因为删除它不会影响任何红黑树的性质,所以直接删除即可, 但是对于删除叶子黑节点就非常复杂,我放一张红黑树的删除操作逻辑图和二叉搜索树的删除逻辑在这里,有兴趣的朋友可以参考研究一下,这里就不详细展开了:
结语
希望这篇关于 红黑树(RB-Tree) 的博客能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】什么是平衡二叉搜索树(AVL Tree)?
【C++】STL标准模板库容器map
【C++】STL标准模板库容器set
【C++】模拟实现二叉搜索(排序)树
【数据结构】C语言实现链式二叉树(附完整运行代码)
【数据结构】什么是二叉搜索(排序)树?
【C++】模拟实现priority_queue(优先级队列)
【C++】模拟实现queue
【C++】模拟实现stack
【C++】模拟实现list
【C++】模拟实现vector
【C++】标准库类型vector
【C++】模拟实现string类
【C++】标准库类型string
【C++】构建第一个C++类:Date类
【C++】类的六大默认成员函数及其特性(万字详解)
【C++】什么是类与对象?

相关文章:

【数据结构】什么是红黑树(Red Black Tree)?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌红黑树的概念 📌红黑树的操作 🎏红黑树的插入操作 🎏红黑树的删除操作 结语 📌红黑树的概念 我们之前学过了…...

Xcode16适配
1.问题,第三方库报错信息如下: Declaration of sa_family_t must be imported from module Darwin.POSIX.sys.types._sa_family_t before it is required2.解答,在报错文件中导入以下头文件 #import <sys/_types/_sa_family_t.h>如有…...

Vue - 路由用法
前端路由就是URL中的hash与组件之间的对应关系。Vue Router是Vue的官方路由。 组成: VueRouter:路由器类,根据路由请求在路由视图中动态渲染选中的组件。<router-link>:请求链接组件,浏览器会解析成<a>。…...

SpringBoot框架下校园资料库的构建与优化
1系统概述 1.1 研究背景 如今互联网高速发展,网络遍布全球,通过互联网发布的消息能快而方便的传播到世界每个角落,并且互联网上能传播的信息也很广,比如文字、图片、声音、视频等。从而,这种种好处使得互联网成了信息传…...

vscode 连接云服务器(ubantu 20.04)
更改服务器系统 如果云服务器上的系统不是ubantu20.04的,可以进行更改: 登录云服务官网(这里以阿里云为例)点击控制台 点击服务器实例 点击更多操作、重置系统 点击重置为其他镜像、系统镜像:选择你要使用的系统镜像…...
【SpringBoot详细教程】-09-Redis详细教程以及SpringBoot整合Redis【持续更新】
🌲 Redis 简介 🌾 什么是Redis Redis 是C语言开发的一个开源高性能键值对的内存数据库,可以用来做数据库、缓存、消息中间件等场景,是一种NoSQL(not-only sql,非关系型数据库)的数据库 Redis是互联网技术领域使用最为广泛的存储中间件,它是「Remote DictionaryServic…...

排序算法之——归并排序,计数排序
文章目录 前言一、归并排序1. 归并排序的思想2. 归并排序时间复杂度及空间复杂度3. 归并排序代码实现1)递归版本2)非递归版本 二、计数排序1. 计数排序的思想2. 计数排序的时间复杂度及空间复杂度3. 计数排序代码实现 总结(排序算法稳定性&am…...

Linux中环境变量
基本概念 环境变量Environmental variables一般是指在操作系统中用来指定操作系统运行环境一些参数。 我们在编写C、C代码时候,在链接的时候从来不知道我们所链接的动态、静态库在哪里。但是还是照样可以链接成功。生成可执行程序。原因就是相关环境变量帮助编译器…...
163页PPT罗兰贝格品牌战略升级:华为案例启示与电器集团转型之路
罗兰贝格作为一家全球顶级的战略管理咨询公司,其品牌战略升级理念在多个行业中得到了广泛应用。以下将以华为案例为启示,探讨电器集团的转型之路,并融入罗兰贝格品牌战略升级的思想。 一、华为案例的启示 华为与罗兰贝格联合撰写的《数据存…...

系统设计,如何设计一个秒杀功能
需要解决的问题 瞬时流量的承接防止超卖预防黑产避免对正常服务的影响兜底方法 前端设计 利用 CDN 缓存静态资源,减轻服务器的压力在前端随机限流按钮防抖,防止用户重复点击 后端设计 Nginx 做统一接入,进行负载均衡与限流用 sentinel 等…...

Linux:进程入门(进程与程序的区别,进程的标识符,fork函数创建多进程)
往期文章:《Linux:深入了解冯诺依曼结构与操作系统》 Linux:深入理解冯诺依曼结构与操作系统-CSDN博客 目录 1. 概念 2. 描述进程 3. 深入理解进程的本质 4. 进程PID 4.1 指令获取PID 4.2 geipid函数获取PID 4.3 kill指令终止进程 …...

索尼MDR-M1:超宽频的音频盛宴,打造沉浸式音乐体验
在音乐的世界里,每一次技术的突破都意味着全新的听觉体验。 索尼,作为音频技术的先锋,再次以其最新力作——MDR-M1封闭式监听耳机,引领了音乐界的新潮流。 这款耳机以其超宽频播放和卓越的隔音性能,为音乐爱好者和专…...

【Linux】线程的概念
一、线程的概念 1.1 什么是线程 在一个程序里的一个执行路线就叫做线程,更准确的定义是:线程是“一个进程内部的控制序列”一切进程至少都有一个执行线程线程在进程内部运行,本质是在进程地址空间内运行在Linux系统中,在CPU眼中…...

centos7.9环境下mysql8数据库双机互备环境部署
为了实现mysql数据库的高可用性,数据库采用双机互备方式部署。双机互备能够避免单点故障造成的系统故障,由于两个节点都可以进行读写,同时也可以提高整个系统的数据读写并发性能。 1. 数据库安装 centos7安装mysql8 community 服务器IP:192.168.76.84 服务器IP:192.16…...

git 报错git: ‘remote-https‘ is not a git command. See ‘git --help‘.
报错内容 原因与解决方案 第一种情况:git路径错误 第一种很好解决,在环境变量中配置正确的git路径即可; 第二种情况 git缺少依赖 这个情况,网上提供了多种解决方案。但如果比较懒,可以直接把仓库地址的https改成ht…...
)
mysql学习教程,从入门到精通,SQL GROUP BY 子句(31)
1、SQL GROUP BY 子句 当然!在SQL中,GROUP BY 子句用于将结果集中的多个记录组合成一个摘要记录。通常,它用于结合聚合函数(如 COUNT(), SUM(), AVG(), MAX(), MIN() 等)来计算每个组的汇总信息。以下是一个详细的例子…...

pip 和 conda 的安装区别
在决定使用 pip 和 conda 安装包时,了解这两个包管理器之间的主要区别非常重要。以下是细分: 1. 区别 1.1. Package Management System 包裹管理系统 Pip: : Primarily used for Python packages. 主要用于 Python 包。 Installs package…...

大学生就业招聘:Spring Boot系统的架构分析
大学生就业招聘系统的设计与实现 摘要 随着信息互联网信息的飞速发展,大学生就业成为一个难题,好多公司都舍不得培养人才,只想要一专多能之人才,不愿是承担社会的责任,针对这个问题开发一个专门适应大学生就业招聘的网…...
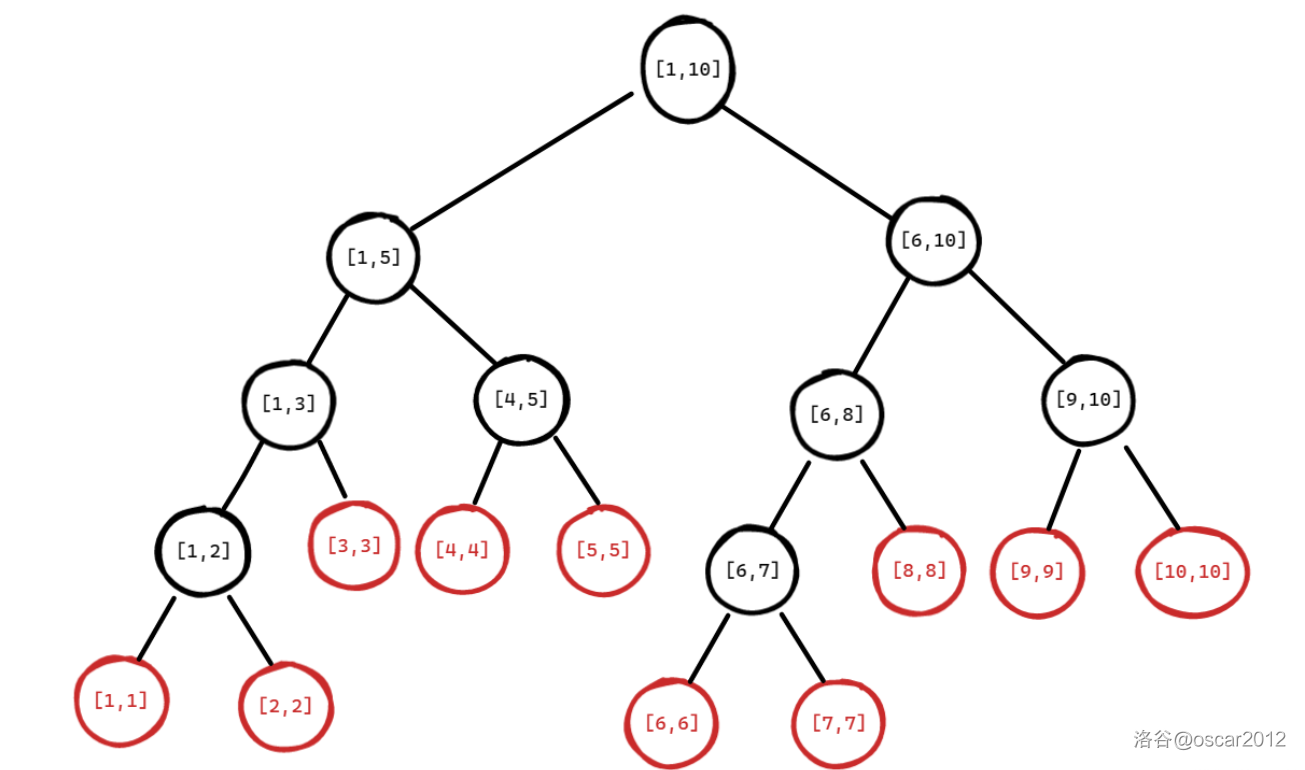
线段树模板
文章目录 线段树练习题目线段树概念区间维护辅助函数创建线段树 :build修改线段树 :modify查询线段树:query 全部代码 线段树 练习题目 洛谷题单 【模板】线段树 1 【模板】线段树 2 开关 扶苏的问题 线段树概念 线段树是一种高级数据结构&a…...

【TypeScript】知识点梳理(三)
#void前面提到了代表空,但有个特殊情况,是空不是空,细谈是取舍,但我们不深究hhh# 代码示例: type func () > voidconst f1: func function() {return true; } 定义了空,返回非空值,理论…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...







































