Mahalanobis distance 马哈拉诺比斯距离
马哈拉诺比斯距离(Mahalanobis Distance)是一种衡量点与分布之间距离的度量,尤其适用于多维数据。与欧几里得距离不同,马哈拉诺比斯距离考虑了数据的协方差结构,因此在统计分析和异常值检测中非常有用。
定义
给定一个数据点 x \mathbf{x} x 和均值 μ \mathbf{\mu} μ,以及数据的协方差矩阵 S \mathbf{S} S,马哈拉诺比斯距离定义为:
D M ( x , μ ) = ( x − μ ) T S − 1 ( x − μ ) D_M(\mathbf{x}, \mathbf{\mu}) = \sqrt{(\mathbf{x} - \mathbf{\mu})^T \mathbf{S}^{-1} (\mathbf{x} - \mathbf{\mu})} DM(x,μ)=(x−μ)TS−1(x−μ)
特点
- 尺度不变性:马哈拉诺比斯距离对不同特征的尺度不敏感,适合高维数据。
- 考虑协方差:通过使用协方差矩阵,可以捕捉到特征之间的相关性。
- 适用于多维数据:在多维空间中,马哈拉诺比斯距离可以有效区分正常数据和异常值。
应用
- 异常值检测:可以用于识别远离均值的点,判断其是否为异常值。
- 聚类分析:在聚类算法中使用马哈拉诺比斯距离能够提高聚类结果的准确性。
- 分类问题:在某些分类算法中,使用马哈拉诺比斯距离可以改进分类性能。
马哈拉诺比斯距离是一种强大的距离度量,特别是在处理具有相关特征的数据时。
相关文章:

Mahalanobis distance 马哈拉诺比斯距离
马哈拉诺比斯距离(Mahalanobis Distance)是一种衡量点与分布之间距离的度量,尤其适用于多维数据。与欧几里得距离不同,马哈拉诺比斯距离考虑了数据的协方差结构,因此在统计分析和异常值检测中非常有用。 定义 给定一…...

R语言绘制直方图
直方图是一种统计图表。它将数据分成若干区间,统计每个区间内数据的数量或频率,用矩形条高度表示。能直观展现数据分布特征,如集中趋势、离散程度等。在数据分析、质量控制、市场调研等领域广泛应用,可帮助人们快速了解数据整体形…...

论文阅读笔记-LogME: Practical Assessment of Pre-trained Models for Transfer Learning
前言 在NLP领域,预训练模型(准确的说应该是预训练语言模型)似乎已经成为各大任务必备的模块了,经常有看到文章称后BERT时代或后XXX时代,分析对比了许多主流模型的优缺点,这些相对而言有些停留在理论层面,可是有时候对于手上正在解决的任务,要用到预训练语言模型时,面…...

求二叉树的带权路径长度
二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和。给定一棵二叉树T,采用二叉链表存储。结点结构为: 其中叶结点的weight域保存该结点的非负权值。设root为指向T的根结点的指针,请设计求T的WPL的算法…...
)
Hive数仓操作(十五)
Hive 开窗函数 Hive窗口函数是一种特殊的函数,允许用户在查询中对一组行进行计算,而不仅仅是单独的行。窗口函数可以在 SQL 查询中进行聚合、排名、累积计算等。这使得窗口函数在数据分析和报告生成中非常有用。 窗口函数的基本组成部分 函数类型&…...

No.12 笔记 | 网络基础:ARP DNS TCP/IP与OSI模型
一、计算机网络:安全的基石 1. 网络的本质:数字世界的神经系统 定义:计算机的互联互通,实现资源共享和信息交换组成要素:发送者、接收者、介质、数据、协议(五大要素) 2. 网络架构࿱…...

OpenHarmony(鸿蒙南向开发)——轻量系统STM32F407芯片移植案例
往期知识点记录: 鸿蒙(HarmonyOS)应用层开发(北向)知识点汇总 鸿蒙(OpenHarmony)南向开发保姆级知识点汇总~ 持续更新中…… 介绍基于STM32F407IGT6芯片在拓维信息 Niobe407 开发板上移植OpenH…...

简单易懂的springboot整合Camunda 7工作流入门教程
简单易懂的Spring Boot整合Camunda7入门教程 因为关于Spring Boot结合Camunda7的教程在网上比较少,而且很多都写得有点乱,很多概念写得太散乱,讲解不清晰,导致看不懂,本人通过研究学习之后就写出了这篇教学文档。 介…...
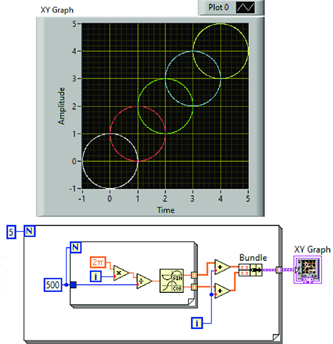
LabVIEW提高开发效率技巧----点阵图(XY Graph)
在LabVIEW开发中,点阵图(XY Graph) 是一种强大的工具,尤其适用于需要实时展示大量数据的场景。通过使用点阵图,开发人员能够将实时数据可视化,帮助用户更直观地分析数据变化。 1. 点阵图的优势 点阵图&…...

C++-匿名空间
匿名命名空间(anonymous namespace)是 C 中的一种特性,用于将符号(如变量、函数或类)限制在定义它们的源文件的作用域内。这意味着在该源文件外部,这些符号不可见,从而避免了命名冲突。 1. 定义…...

jdk的安装和环境变量配置
1.将从官网下载好的jdk放在自己想要放的位置,这里的位置是:E:\develop 2.新建一个文件夹用来放安装的jdk,将jdk安装的此目录,这里的位置是:E:\develop\jdk17 3.jdk安装好之后,点击jdk17目录,点…...

继承、Lambda、Objective-C和Swift
继承 东风系列导弹是镇国神器。东风41不是突然就造出来的,之前有很多种东风xx导弹,每种导弹都有自己的独特之处,相同之处都具备导弹基本特点。很多工厂有量产磨具的生产线,盖房子就图纸,建筑设计建设都有参考ÿ…...

设置服务器走本地代理
勾选: 然后: git clone https://github.com/rofl0r/proxychains-ng.git./configure --prefix/home/wangguisen/usr --sysconfdir/home/wangguisen/etcmakemake install# 在最后配置成本地代理地址 vim /home/wangguisen/etc/proxychains.confsocks4 17…...

刷题 -哈希
面试面试经典 150 题 - 哈希 383. 赎金信 - 一个哈希表搞定 class Solution { public:bool canConstruct(string ransomNote, string magazine) {int hash[26] {0};for (auto& ch : magazine) {hash[ch - a];}for (auto& ch : ransomNote) {if (--hash[ch - a] < …...

React响应式修改数组和对象
在React中,响应式地修改数组数据是一个常见的需求,它涉及到状态(state)的管理和更新。React的状态是不可变的,这意味着你不能直接修改状态对象中的数组元素,而是需要创建一个新的数组来更新状态。下面将详细…...

cerbot https证书免费自动续期
1. 简介 cerbot是一个开源的数字证书生成平台,简单好用。下面我们来看下安装配置和使用。 cerbot有很多种安装方式,有源码安装、第三方发布版本、pip安装和snap安装,官方推荐使用snap安装。 2. snap安装 snap官方安装文档,Sna…...

嵌入式硬件设计
嵌入式硬件设计是指针对嵌入式系统(一种专用的计算机系统,通常嵌入到其他设备中)进行的硬件设计工作。嵌入式系统广泛应用于消费电子、工业控制、医疗设备、汽车电子、航空航天等领域。以下是嵌入式硬件设计的主要内容和步骤: 1.…...

2024.09.24 校招 实习 内推 面经
🛰️ :neituijunsir 交* 流*裙 ,内推/实习/校招汇总表格 1、校招 | 毫末智行2025届校园招聘正式启动 (内推) 校招 | 毫末智行2025届校园招聘正式启动 (内推) 2、校招 | 圭目机器人 2025 校…...

GIT安装及集成到IDEA中操作步骤
最近深感GIT使用技能太差,我只会些皮毛,还是得看官网,总结一下常用的操作方法吧。 GIT环境配置到IDEA中安装 一、GIt的基本的安装 这个不在这里赘述了,自己装一个git吧 二、给IDEA指定本地GIT的安装路径 1、下图这个是我本地的…...

Java使用线程池创建线程
一、线程前言 首先我们知道,线程的概念如果不知道可以去看这一篇Java中的线程,我们这篇主要讲述的是Java怎么使用线程池创建线程,首先我们要对线程池有点概念,其实顾名思义,线程池就是有喝多线程的一个池子类似于&…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...
