3956. 截断数组
3956. 截断数组 - AcWing题库
3956. 截断数组
【题目描述】
给定一个长度为 nn 的数组 a1,a2,…,ana1,a2,…,an。
现在,要将该数组从中间截断,得到三个非空子数组。
要求,三个子数组内各元素之和都相等。
请问,共有多少种不同的截断方法?
【输入】
第一行包含整数 nn。
第二行包含 nn 个整数 a1,a2,…,ana1,a2,…,an。
【输入】
输出一个整数,表示截断方法数量。
数据范围
前六个测试点满足 1≤n≤10;1≤n≤10。
所有测试点满足 1≤n≤;1≤n≤
,−10000≤
≤10000;−10000≤
≤10000。
解题思路:
因为题意是由一个不变的数组,截成三段,所以这个数组的总和 sum 是相等的,其中截成的三段的值要都相等,那么这三段应该截成的三段它们的和应该满足: sum1==sum2==sum3==sum/3 .首先想到的是用前缀和,后缀和,因为要判断的情况太多了,刚开始是这么写的:
大概是先判断前缀和到达 sum1==sum/3 的时候就判断后缀和,但是会有漏掉的情况,因为 i 层的循环是一直自增的,判断完第一段满足要求后,接着要遍历后一段满足要求的区域,此时可以用数组来存储后一段满足条件的 sum3==sum 的部分(数据过大时可能会重复计算很多遍),而且还要保证统计出来的数量没有重复的部分。
一直在改的错误代码:
#include<stdio.h>
int a[100005],book[100005];
int main(){int n,sum=0;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);sum=sum+a[i];}int x=sum/3;if(sum%3!=0){printf("0\n");return 0;}int S=0;int sum1=0,sum2=0;int k=n-1,i,j;for(i=0;i<n;i++){sum1=sum1+a[i];if(sum1==x){for(k=n-1;k>i+1;k--){if(sum2==x){S++;book[k]=1;}sum2=sum2+a[k];n--;if(book[k]==0&&sum2==x){S++;book[k]=0;}}}} printf("%d\n",S);return 0;
} 然后,看到题解,写的很简单。(sum 是数组的总和)
他的思路是记录前缀和(sum1)中满足 sum1==sum/3 的部分(也就是第一次截断的点)以及满足 sum1==sum/3*2 的部分(第二次截断的点)。
数据有些大,要开 long long 存储。
#include<stdio.h>
int a[100005];
int main(){int n,x,sum=0;scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);sum=sum+a[i];}x=sum/3;long long S=0,ans=0;long long flag=0;if(sum%3!=0||n<3){printf("0\n");return 0;}for(int i=0;i<n-1;i++){//第二次截断后,第三个位置不能为空 S=S+a[i];if(S==2*x)ans=ans+flag;if(S==x)flag++;}printf("%lld\n",ans);return 0;
}795.前缀和

代码如下:
#include<stdio.h>
int sum[100005];
int main(){int a,b,x,n,m;scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){scanf("%d",&x);sum[i]=sum[i-1]+x;} for(int i=0;i<m;i++){scanf("%d%d",&a,&b);printf("%d\n",sum[b]-sum[a-1]);}return 0;
}796.子矩阵的和

代码如下:
#include<stdio.h>
int a[1005][1005],sum[1005][1005];
int main(){int x,y,z,w,i,j,n,m,k;scanf("%d%d%d",&n,&m,&k);for(i=1;i<=n;i++){for(j=1;j<=m;j++){scanf("%d",&a[i][j]);}}for(i=1;i<=n;i++){for(j=1;j<=m;j++){sum[i][j]=a[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];}}for(i=0;i<k;i++){scanf("%d%d%d%d",&x,&y,&z,&w);printf("%d\n",sum[z][w]-sum[x-1][w]-sum[z][y-1]+sum[x-1][y-1]);}
}
相关文章:

3956. 截断数组
3956. 截断数组 - AcWing题库 3956. 截断数组 【题目描述】 给定一个长度为 nn 的数组 a1,a2,…,ana1,a2,…,an。 现在,要将该数组从中间截断,得到三个非空子数组。 要求,三个子数组内各元素之和都相等。 请问,共有多少种不同…...

React Labs: 我们最近在做什么——2023 年 3 月
原文:https://react.dev/blog/2023/03/22/react-labs-what-we-have-been-working-on-march-2023 React Server Components React Server Components(下文简称 RSC) 是由 React 团队设计的新应用程序架构。 我们首先在一个介绍性演讲和一个RFC中分享了我们对 RSC 的…...
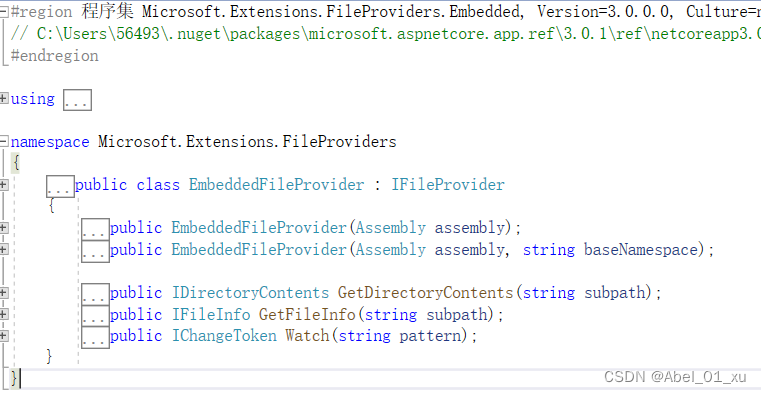
文件系统设计详解
抽象的文件系统以目录的形式来组织文件,我们可以利用该文件系统来读取某个文件的内容,也可以对目录或者文件实施监控并及时获取变化的通知。 IChangeToken IChangeToken对象就是一个与某组监控数据相关联的“令牌”(Token)&#x…...

好看~立马启动python实现美女通通下
人生苦短,我用python一、环境版本使用二、代码实现思路三、代码展示:导入模块伪装(请求头)四、部分好看截图,更多的就自己去采集噜~吃饭放松的时候哇一不小心看见了很多好看的东西 哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈 独乐乐不如众乐乐…...
Git 安装设置
1、安装 安装以下三个软件: Git-2.13.3-64-bit.exe TortoiseGit-2.4.0.2-64bit.msi TortoiseGit-LanguagePack-2.4.0.0-64bit-zh_CN.msi 安装过程中不用填写、不用选择,全部点"下一步",完成后需要重启机器。 2、基本设…...

Python-闭包
介绍 Python的闭包是一种高级的编程技巧,它可以在函数内部定义另一个函数,并返回该函数的引用。这个内部函数可以访问外部函数的变量和参数,即使外部函数已经执行完毕 好处 1)闭包可以避免全局变量的污染,使得代码更…...

Gitlab中Pipeline语法四
Gitlab中Pipeline语法 cache cache:paths 在job build中定义缓存,将会缓存target目录下的所有*.jar文件当全局定义了cache:paths会被job中覆盖.以下实例将缓存target目录 buld:script: buildcache:paths:- target/*.jar#设置key可以解决cache被覆盖 cache:paths:- my/files…...
第五章)
Go语言精修(尚硅谷笔记)第五章
五、程序流程控制 5.1 单分支控制 package main import ("fmt" )func main() {//请大家看个案例[ifDemo.go]://编写一个程序,可以输入人的年龄,如果该同志的年龄大于18岁,则输出 "你年龄大//于18,要对自己的行为负责!"//分析 //1.年龄 > var age int…...
)
三、MySQL 高级(DML 增删改)
三、MySQL 高级(DML 增删改) 3.1 DML 数据操纵语言 DML(Data Manipulation Language)DML对数据库中表记录的执行操作 插入(INSERT) 插入单行数据 插入多行数据 将查询结果插入到新表 更新(…...

面向AI编程的本质是什么?
面向AI编程的本质是什么? 面向AI编程的本质是编程的第五代编程语言,与自然语言非常相似,但是是有区别的。 因此出现了针对与AI通话的提示工程。 简单地回顾一下编程语言的发展史, 第一代编程语言是机器语言,它直接使…...

深入浅出——深度学习训练中的warmup
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
你知道如何用C语言将格式化数据和字符串相互转换吗?
今天重点介绍2个函数,分别是sprintf和sscanf,用来将格式化数据和字符串相互转换。它们的作用分别是: sprintf函数用于将格式化数据转换成字符串。sscanf函数用于将字符串转换成格式化数据。 接下来是第一个大问题:我怎么记忆呢&…...

免费一键生成原创文章-原创文章批量生成
免费使用一键生成原创文章,轻松解决写作难题! 您是否因为写作枯竭、文章档次不高,而感到烦恼?现在,我们有一个免费的文章创作工具,帮助您无需付出太多的努力就能高效地创造原创文章。 一键生成࿱…...

【数据库管理】④重做日志Redo Log
1. Redo log(重做日志)的功能 重做日志(Redo log)是数据库管理系统中的一种机制,主要作用包括: 提供事务的持久性支持:重做日志记录了每个事务对数据库所做的修改操作,以便在系统故障或崩溃时,通…...
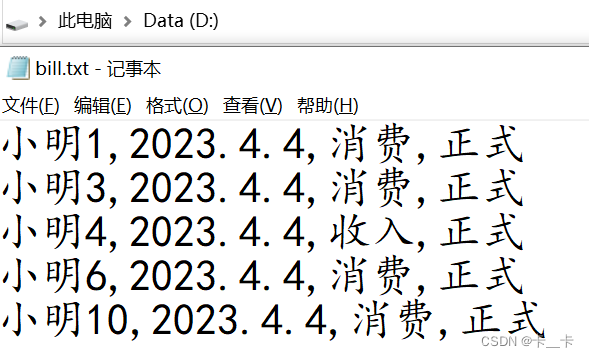
5-python文件操作
文章目录1.打开文件2.文件读取3.文件关闭4.文件写入/追加1.打开文件 当传参顺序不一致时,不能使用位置传参,应使用关键字传参 open(file, mode‘r’, buffering-1, encodingNone, errorsNone, newlineNone, closefdTrue, openerNone) 通常使用…...
企业级Oracle入门Linux/Unix基础①
1、了解计算机系统的组成、操作系统介绍、IT技术发展与云计算、服务器的分类、存储设备介绍、常用的主机存储有哪些? 1.1 计算机系统的组成: 计算机系统由硬件和软件两部分组成。硬件包括中央处理器(CPU)、内存、输入输出设备、…...
NexNoSQL Client:Elasticsearch、Redis、MongoDB三合一的可视化客户端管理工具
背景: 工作中我们使用了Elasticsearch作为存储,来支持内容的搜索,Elasticsearch这个软件大家都耳熟能详,它是一个分布式、高扩展、高实时的搜索与数据分析引擎,不仅仅支持文本索引,还支持聚合操作…...

如果大学能重来,我绝对能吊打90%的大学生,早知道这方法就好了
最近收到很多大学生粉丝的私信,大多数粉丝们都迷茫着大学计算机该怎么学,毕业后才能找到好工作。 可能是最近回答这方面的问题有点多,昨晚还真梦回大学…其实工作了20多年,当过高管,创过业,就差没写书了。…...

FactoryBean是现在的执行时机
调用getBean方法,最终到org.springframework.beans.factory.support.DefaultListableBeanFactory#preInstantiateSingletons方法: for (String beanName : beanNames) {RootBeanDefinition bd getMergedLocalBeanDefinition(beanName);if (!bd.isAbstr…...
自定义注解使用
现象: 自定义注解使用 方法: 1:元注解 java.lang.annotation 下定义了元注解 Documented 文档相关 标注了此注解则会包含在javadoc文档中Retention 指定注解生命周期Target 指定注解作用范围Inherited 指定子类可以继承父类的注解Native …...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
