快速排序算法
一:快速排序思想


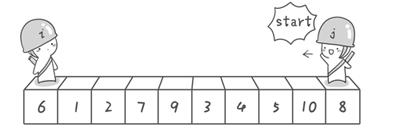
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数,待会你就知道它用来做啥的了)。为了方便,就让第一个数6作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在6的右边,比基准数小的数放在6的左边,类似下面这种排列:
3 1 2 5 4 6 9 7 10 8
在初始状态下,数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置,假设这个位置是k。现在就需要寻找这个k,并且以第k位为分界点,左边的数都小于等于6,右边的数都大于等于6。想一想,你有办法可以做到这点吗?
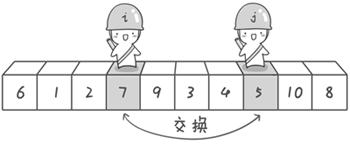
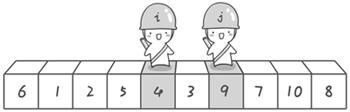
方法其实很简单:分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。这里可以用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边(即i=1),指向数字6。让哨兵j指向序列的最右边(即=10),指向数字。
首先哨兵j开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵j先出动,这一点非常重要(请自己想一想为什么)。哨兵j一步一步地向左挪动(即j–),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。
现在交换哨兵i和哨兵j所指向的元素的值。交换之后的序列如下:
6 1 2 5 9 3 4 7 10 8
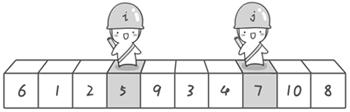
到此,第一次交换结束。接下来开始哨兵j继续向左挪动(再友情提醒,每次必须是哨兵j先出发)。他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动的,他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换,交换之后的序列如下:
6 1 2 5 4 3 9 7 10 8
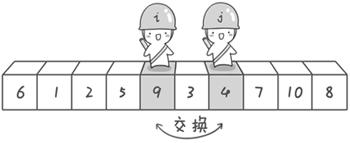
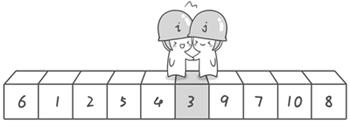
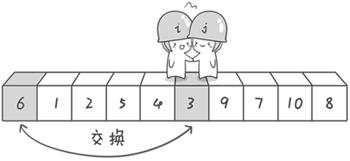
第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下:
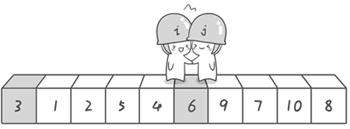
3 1 2 5 4 6 9 7 10 8
到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。回顾一下刚才的过程,其实哨兵j的使命就是要找小于基准数的数,而哨兵i的使命就是要找大于基准数的数,直到i和j碰头为止。
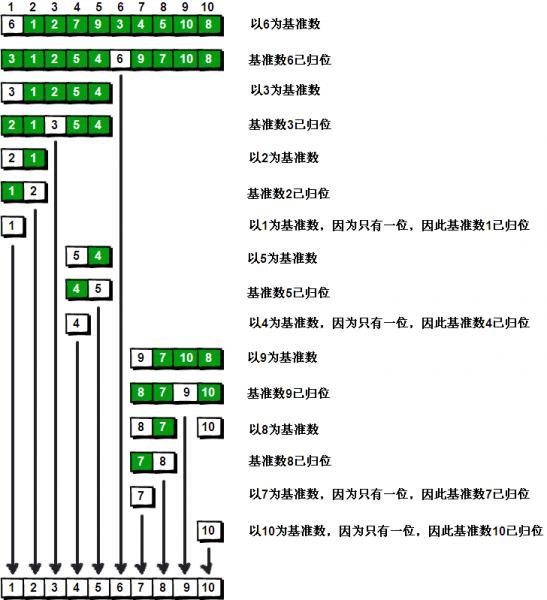
OK,解释完毕。现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。接下来还需要分别处理这两个序列。因为6左边和右边的序列目前都还是很混乱的。不过不要紧,我们已经掌握了方法,接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。现在先来处理6左边的序列现吧。
左边的序列是“3 1 2 5 4”。请将这个序列以3为基准数进行调整,使得3左边的数都小于等于3,3右边的数都大于等于3。好了开始动笔吧
如果你模拟的没有错,调整完毕之后的序列的顺序应该是:
2 1 3 5 4
OK,现在3已经归位。接下来需要处理3左边的序列“2 1”和右边的序列“5 4”。对序列“2 1”以2为基准数进行调整,处理完毕之后的序列为“1 2”,到此2已经归位。序列“1”只有一个数,也不需要进行任何处理。至此我们对序列“2 1”已全部处理完毕,得到序列是“1 2”。序列“5 4”的处理也仿照此方法,最后得到的序列如下:
1 2 3 4 5 6 9 7 10 8
对于序列“9 7 10 8”也模拟刚才的过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列,如下
1 2 3 4 5 6 7 8 9 10
到此,排序完全结束。细心的同学可能已经发现,快速排序的每一轮处理其实就是将这一轮的基准数归位,直到所有的数都归位为止,排序就结束了。下面上个霸气的图来描述下整个算法的处理过程。
这是为什么呢?
快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。因此总的比较和交换次数就少了,速度自然就提高了。当然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(N2),它的平均时间复杂度为O(NlogN)。其实快速排序是基于一种叫做“二分”的思想。我们后面还会遇到“二分”思想,到时候再聊。先上代码,如下
二:快速排序代码(pivot一定时先和arrays【r】先比较)
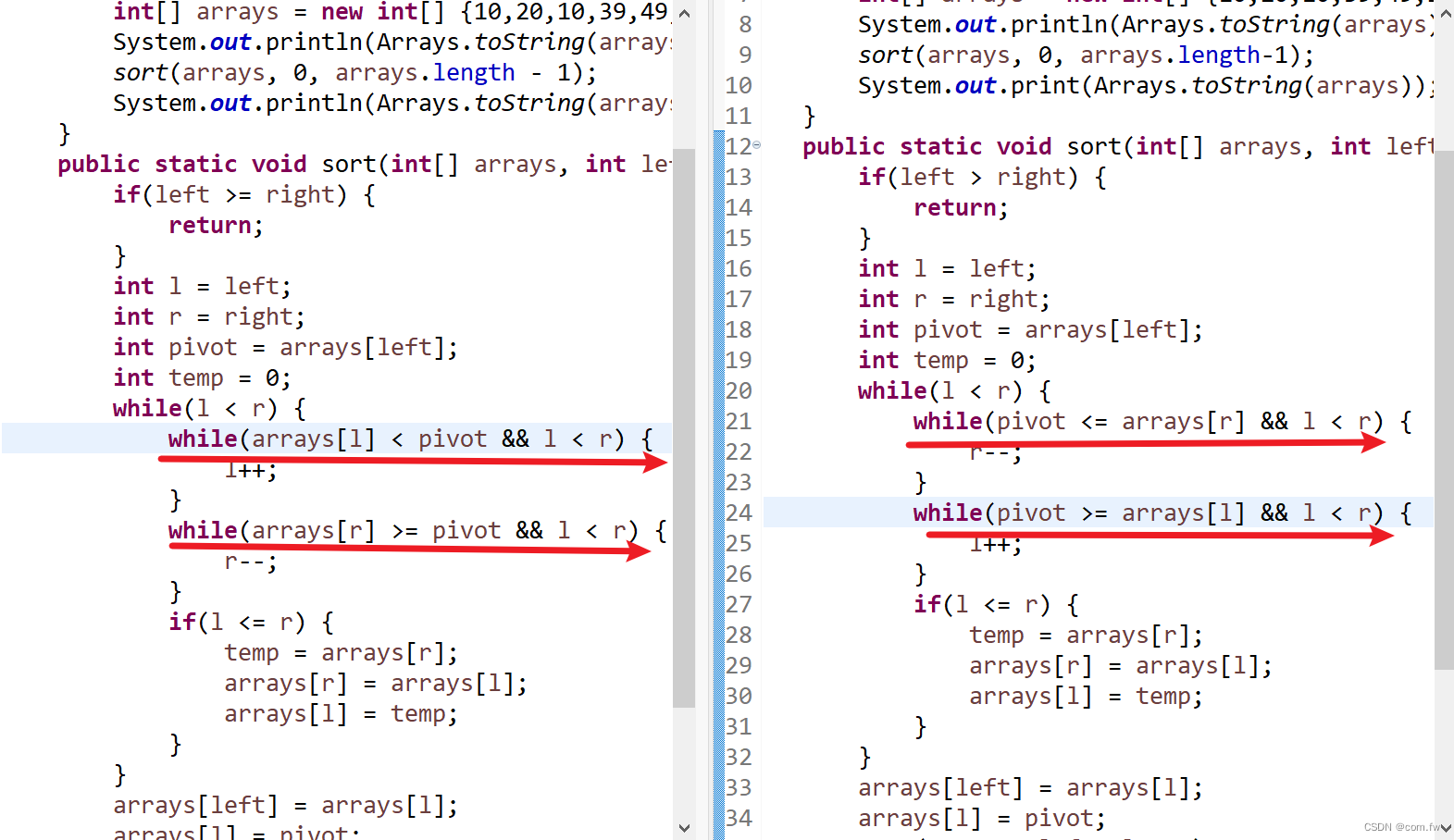
public static void sort(int[] arrays, int left, int right) {if(left > right) {return;}int l = left;int r = right;int pivot = arrays[left];int temp = 0;while(l < r) {while(pivot <= arrays[r] && l < r) {r--;}while(pivot >= arrays[l] && l < r) {l++;}if(l <= r) {temp = arrays[r];arrays[r] = arrays[l];arrays[l] = temp;}}arrays[left] = arrays[l];arrays[l] = pivot;sort(arrays, left, l - 1);sort(arrays, l + 1, right); }三:结果

相关文章:

快速排序算法
一:快速排序思想 假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数,待会你就知道它用来做啥的了)。为了方便ÿ…...
)
中华好诗词大学季第二季(四)
第七期 1,二十四友一朝尽,爱妾坠楼何足言出自许浑的《金谷园》,“爱妾”指的是谁 2,李白在《九月十日即事》借菊花表达自己的惋惜之情,请问九月十日是什么节日 A 后登高 B 菊花节 C 小重阳 3,贾宝玉在大观园里面题了“曲径通幽”…...

分布式系统容灾部署方案
本文主要以OceanBase部署来说明分布式系统容灾部署方案 分布式系统提供持续可用的服务尤为重要。 好的分布式系统根据需求提供不同等级的的高可用与容灾级别。 而在分布式系统中,数据库系统又是最核心最关键的系统。 我们以数据库分布式系统为主,考虑…...

Python 爬虫性能相关总结
这里我们通过请求网页例子来一步步理解爬虫性能 当我们有一个列表存放了一些url需要我们获取相关数据,我们首先想到的是循环 简单的循环串行 这一种方法相对来说是最慢的,因为一个一个循环,耗时是最长的,是所有的时间总和 代码…...
Baumer工业相机堡盟工业相机如何设置网口的IP地址(工业相机连接的网口设置IP地址步骤)
Baumer工业相机堡盟工业相机如何设置网口的IP地址(工业相机连接的网口设置IP地址步骤)Baumer工业相机Baumer工业相机设置网络端口IP地址匹配设置网络端口IP地址和工业相机IP地址匹配第一次打开CameraExplorer软件确认问题为IP地址不匹配问题打开网络连接…...

Android MediaCodec设置H264 Profile到High
H264 High Profile压缩率高,能降低码率,这里记录下MediaCodec Profile设置到High遇到的一些问题。 Android 4.1 就引入了MediaCodecInfo.CodecProfileLevel类,下面截取H264(AVC)的Profile和Level定义: /** Copyright (C) 2012 The Android O…...
)
QT之QSysInfo(查看电脑信息)
文章目录前言一、API使用总结前言 QSysInfo是Qt中用于获取有关运行应用程序的系统信息的类。 我们可以获取以下信息: 返回系统产品类型,如ios,windows,Linux等 返回当前系统的产品版本。 返回当前系统的内核类型。 返回当前系统的…...

中国塑料编织袋产业竞争状况及投资前景预测报告2023-2029年
中国塑料编织袋产业竞争状况及投资前景预测报告2023-2029年 KKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKK 《报告编号》: BG451639 《出版时间》: 2023年4月 《出版机构》: 中智正业研究院 免费售后 服务一年,具体内容及订购流程欢迎咨询客服人员 内容简介&…...

从头用脚分析FFmpeg源码 - av_read_frame
av_read_frame作用 /*** Return the next frame of a stream.* This function returns what is stored in the file, and does not validate* that what is there are valid frames for the decoder. It will split what is* stored in the file into frames and return one f…...

第17章_触发器
第17章_触发器 🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目前在某公…...

3956. 截断数组
3956. 截断数组 - AcWing题库 3956. 截断数组 【题目描述】 给定一个长度为 nn 的数组 a1,a2,…,ana1,a2,…,an。 现在,要将该数组从中间截断,得到三个非空子数组。 要求,三个子数组内各元素之和都相等。 请问,共有多少种不同…...

React Labs: 我们最近在做什么——2023 年 3 月
原文:https://react.dev/blog/2023/03/22/react-labs-what-we-have-been-working-on-march-2023 React Server Components React Server Components(下文简称 RSC) 是由 React 团队设计的新应用程序架构。 我们首先在一个介绍性演讲和一个RFC中分享了我们对 RSC 的…...
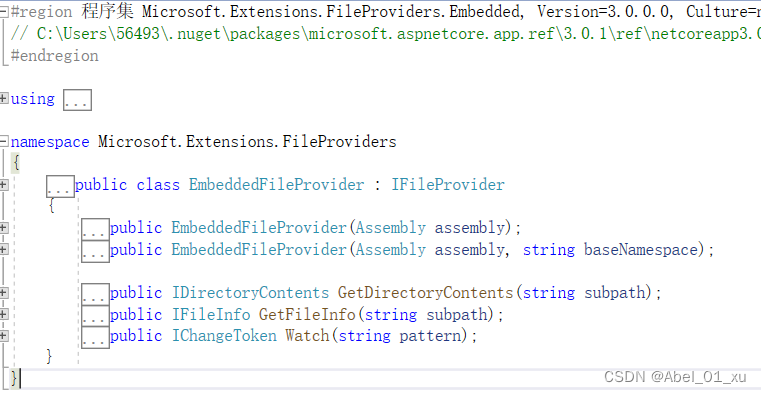
文件系统设计详解
抽象的文件系统以目录的形式来组织文件,我们可以利用该文件系统来读取某个文件的内容,也可以对目录或者文件实施监控并及时获取变化的通知。 IChangeToken IChangeToken对象就是一个与某组监控数据相关联的“令牌”(Token)&#x…...

好看~立马启动python实现美女通通下
人生苦短,我用python一、环境版本使用二、代码实现思路三、代码展示:导入模块伪装(请求头)四、部分好看截图,更多的就自己去采集噜~吃饭放松的时候哇一不小心看见了很多好看的东西 哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈 独乐乐不如众乐乐…...
Git 安装设置
1、安装 安装以下三个软件: Git-2.13.3-64-bit.exe TortoiseGit-2.4.0.2-64bit.msi TortoiseGit-LanguagePack-2.4.0.0-64bit-zh_CN.msi 安装过程中不用填写、不用选择,全部点"下一步",完成后需要重启机器。 2、基本设…...

Python-闭包
介绍 Python的闭包是一种高级的编程技巧,它可以在函数内部定义另一个函数,并返回该函数的引用。这个内部函数可以访问外部函数的变量和参数,即使外部函数已经执行完毕 好处 1)闭包可以避免全局变量的污染,使得代码更…...

Gitlab中Pipeline语法四
Gitlab中Pipeline语法 cache cache:paths 在job build中定义缓存,将会缓存target目录下的所有*.jar文件当全局定义了cache:paths会被job中覆盖.以下实例将缓存target目录 buld:script: buildcache:paths:- target/*.jar#设置key可以解决cache被覆盖 cache:paths:- my/files…...
第五章)
Go语言精修(尚硅谷笔记)第五章
五、程序流程控制 5.1 单分支控制 package main import ("fmt" )func main() {//请大家看个案例[ifDemo.go]://编写一个程序,可以输入人的年龄,如果该同志的年龄大于18岁,则输出 "你年龄大//于18,要对自己的行为负责!"//分析 //1.年龄 > var age int…...
)
三、MySQL 高级(DML 增删改)
三、MySQL 高级(DML 增删改) 3.1 DML 数据操纵语言 DML(Data Manipulation Language)DML对数据库中表记录的执行操作 插入(INSERT) 插入单行数据 插入多行数据 将查询结果插入到新表 更新(…...

面向AI编程的本质是什么?
面向AI编程的本质是什么? 面向AI编程的本质是编程的第五代编程语言,与自然语言非常相似,但是是有区别的。 因此出现了针对与AI通话的提示工程。 简单地回顾一下编程语言的发展史, 第一代编程语言是机器语言,它直接使…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...