P3197 [HNOI2008] 越狱
题目传送门
题面
[HNOI2008] 越狱
题目描述
监狱有 n n n 个房间,每个房间关押一个犯人,有 m m m 种宗教,每个犯人会信仰其中一种。如果相邻房间的犯人的宗教相同,就可能发生越狱,求有多少种状态可能发生越狱。
答案对 100 , 003 100,003 100,003 取模。
输入格式
输入只有一行两个整数,分别代表宗教数 m m m 和房间数 n n n。
输出格式
输出一行一个整数代表答案。
样例 #1
样例输入 #1
2 3
样例输出 #1
6
提示
样例输入输出 1 解释
| 状态编号 | 1 号房间 | 2 号房间 | 3 号房间 |
|---|---|---|---|
| 1 | 信仰 1 | 信仰 1 | 信仰 1 |
| 2 | 信仰 1 | 信仰 1 | 信仰 2 |
| 3 | 信仰 1 | 信仰 2 | 信仰 2 |
| 4 | 信仰 2 | 信仰 1 | 信仰 1 |
| 5 | 信仰 2 | 信仰 2 | 信仰 2 |
| 6 | 信仰 2 | 信仰 2 | 信仰 1 |
数据规模与约定
对于 100 % 100\% 100% 的数据,保证 1 ≤ m ≤ 1 0 8 1 \le m \le 10^8 1≤m≤108, 1 ≤ n ≤ 1 0 12 1 \le n \le 10^{12} 1≤n≤1012。
思路
先正常看,题目难度普及/提高,所以有很大的思维成分在里面。
然后的话这是标签:

明显这是一道排列组合题目。
先考虑会越狱情况下的各种情况
这是样例1的
| 状态编号 | 1 号房间 | 2 号房间 | 3 号房间 |
|---|---|---|---|
| 1 | 信仰 1 | 信仰 1 | 信仰 1 |
| 2 | 信仰 1 | 信仰 1 | 信仰 2 |
| 3 | 信仰 1 | 信仰 2 | 信仰 2 |
| 4 | 信仰 2 | 信仰 1 | 信仰 1 |
| 5 | 信仰 2 | 信仰 2 | 信仰 2 |
| 6 | 信仰 2 | 信仰 2 | 信仰 1 |
很明显,从2个一样信仰的相邻一直到n个一样的信仰相邻都有多种可能,所以从这个方向考虑会很复杂。
那么可以换一种思路,从逆向来想,因为只有两种情况,要么越狱,要么不越狱,所以可以理解为 越狱的情况 = 所有情况 − 不越狱的情况 越狱的情况=所有情况-不越狱的情况 越狱的情况=所有情况−不越狱的情况
那么考虑一下不越狱的情况。
有m中信仰的情况下,具体可以这样分配:
| 1 号房间 | 2 号房间 | 3 号房间 | … | 3n号房间 |
|---|---|---|---|---|
| m种信仰 | m-1种信仰 | m-1种信仰 | m-1种信仰 | m-1种信仰 |
因为为了不和上一个房间的宗教相同,所以剩下了除上一个房间以外m-1种信仰可选,然而第一间左边没有房间可以有m种选择。
因此我们可以把答案弄出来了
a n s = n m − m ∗ ( n − 1 ) m − 1 ans=n^m-m*(n-1)^{m-1} ans=nm−m∗(n−1)m−1
接着看数据范围,保证 1 ≤ m ≤ 1 0 8 1 \le m \le 10^8 1≤m≤108, 1 ≤ n ≤ 1 0 12 1 \le n \le 10^{12} 1≤n≤1012,所以如果用O(n)的时间复杂度会过不了( 1 0 8 10^8 108有的判题机好似可以过)
所以要用快速幂,原理就是倍增思想,时间复杂度降低到了 l o g ( n ) log(n) log(n)
虽然c++本身有快速幂函数pow,不过由于涉及取模,所以需要手写一个。
最后提交上去就会发现有的点WA了,由于这里面取模运算的特性,所以有可能会出现 n m n^m nm取模完以后比后面那一坨还小,这时候我们就应该加上一个模数就可以了
c o d e code code
#include<bits/stdc++.h>
using namespace std;
//#define ll long long防伪认证
#define ld long double
#define FOR(x,a,b,c) for(int x=a;x<=b;x+=c)
#define MFOR(x,a,b,c) for(int x=a;x>=b;x-=c)
#define MPFOR(x,a,b,c) for(int x=a;a<=b;x*=c)
const int N3=1e3+10;
const int N=1e6+10;
const long double esp=1e-8;
bool f[N];
/*/防伪认证
map<ll,int> a;
queue<int> a;
stack<int> a;
priority_queue<int> a;
vector<int> a;
set<int> a;
::iterator it
unordered
/*/
int gcd(int a,int b){int c=a%b;while(a%b!=0){a=b;b=c;c=a%b;}return b;
}
int lcm(int x,int y){return (x*y)/gcd(x,y);
}
void p(int n){f[1]=1;f[0]=1;for(int i=2;i*i<=n;i++){if(f[i]) continue;for(int j=i*i;j<=n;j+=i){f[j]=1;}}
}
ll qpow(ll x,ll y,ll md){//快速幂ll ans=1;while(y){//相当于给他求二进制if(y&1){ans*=x;ans%=md;}x*=x;//倍增思想x%=md;y>>=1;}return ans;
}
ll n,m;
ll ans=1;
int main(){freopen(".in","r",stdin);freopen(".out","w",stdout);ios::sync_with_stdio(false);cin>>m>>n;ans=((qpow(m,n,100003))-m*qpow(m-1,n-1,100003)%100003)%100003;//公式计算if(ans<0) ans+=100003;//特殊情况cout<<ans;fclose(stdin);fclose(stdout);return 0;
}
/*/
思路区
/*/
不要复制以后直接提交,不会AC,会编译错误!!!
相关文章:

P3197 [HNOI2008] 越狱
题目传送门 题面 [HNOI2008] 越狱 题目描述 监狱有 n n n 个房间,每个房间关押一个犯人,有 m m m 种宗教,每个犯人会信仰其中一种。如果相邻房间的犯人的宗教相同,就可能发生越狱,求有多少种状态可能发生越狱。 …...
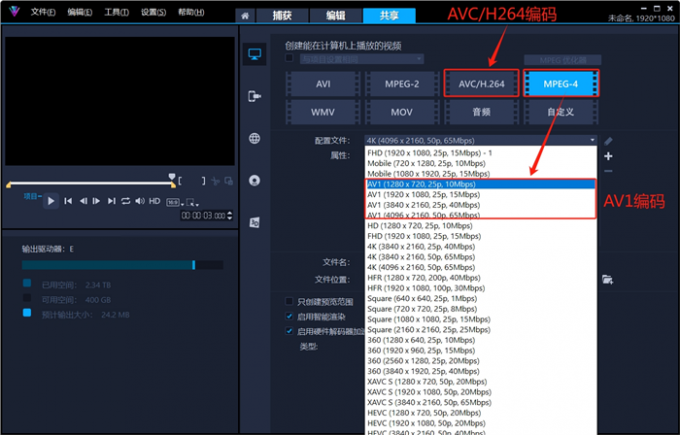
会声会影导出视频mp4格式哪个最高清,会声会影输出格式哪个清晰
调高分辨率后,mp4视频还是不清晰。哪怕全部使用4K级素材,仍然剪不出理想中的高画质作品。不是你的操作有问题,而是剪辑软件没选对。Corel公司拥有全球顶尖的图像处理技术,该公司研发的会声会影视频剪辑软件,在过去的20…...

Linux:进程调度算法和进程地址空间
✨✨✨学习的道路很枯燥,希望我们能并肩走下来! 文章目录 目录 文章目录 前言 一 进程调度算法 1.1 进程队列数据结构 1.2 优先级 编辑 1.3 活动队列 编辑 1.4 过期队列 1.5 active指针和expired指针 1.6 进程连接 二 进程地址空间 2.1 …...

TCP ---滑动窗口以及拥塞窗口
序言 在上一篇文章中我们介绍了 TCP 中的协议段格式,以及保证其可靠传输的重传机制,着重介绍了三次握手建立连接,四次挥手断开连接的过程(👉点击查看)。 这只是 TCP 保证通信可信策略的一部分,现在让我们继续深入吧&…...

第十二章--- fixed 和 setprecision 函数、round 函数、进制转换及底层逻辑
1. 保留几位小数 在C中,如果你想要控制输出的小数点后的位数,可以使用<iomanip>头文件提供的fixed和setprecision函数。这里的fixed用于设置浮点数的输出格式为定点表示法,而setprecision(n)则用来指定小数点后保留的位数。具体用法如…...

ASP.NetCore---I18n(internationalization)多语言版本的应用
文章目录 0.实现的效果如下1.创建新项目I18nBaseDemo2.添加页面中的下拉框3.在HomeController中添加ChangeLanguage方法4.在Progress.cs 文件中添加如下代码:5. 在progress.cs中添加code6.添加Resource资源文件7.在页面中引用i18n的变量8. 重启项目,应该…...

vue3 环境配置vue-i8n国际化
一.依赖和插件的安装 主要是vue-i18n和 vscode的自动化插件i18n Ally https://vue-i18n.intlify.dev/ npm install vue-i18n10 pnpm add vue-i18n10 yarn add vue-i18n10 vscode在应用商城中搜索i18n Ally:如图 二.实操 安装完以后在对应项目中的跟package.jso…...

2024 uniapp入门教程 01:含有vue3基础 我的第一个uniapp页面
uni-app官网uni-app,uniCloud,serverless,快速体验,看视频,10分钟了解uni-app,为什么要选择uni-app?,功能框架图,一套代码,运行到多个平台https://uniapp.dcloud.net.cn/ 准备工作:HBuilder X 软件 HBuilder X 官网下载…...

CentOS 7文件系统
从centos7开始,默认的文件系统从ext4变成了XFS。随着虚拟化的应用越来越广泛,作为虚拟化磁盘来源的大文件(单个文件几GB级别)越来越常见。 1.XFS组成部分: XFS文件系统在数据的分布上主要划分为三部分:数据…...
)
vue源码解析(源码解析学习大纲)
文章目录 Vue源码解析入手方向大纲1.核心概念1-1.响应式系统1-2. 组件1-3. 虚拟DOM1-4. 指令1-5. 生命周期钩子 2.虚拟DOM2-1. 概念2-2. 工作流程2-3. 示例2-4.总结 3.组件系统3-1. 组件的定义3-2. 组件的创建3-3. 组件的模板3-4. 生命周期3-5. 事件处理3-6. 插槽(S…...

工行企业网银U盾展期后有两个证书问题的解决方法
工行企业网银U盾证书快到期后,可以自助展期,流程可以根据企业网银提示页面操作。操作后,可能存在两个新旧两个证书并存的情况,致使网银转账等操作失败,如图: 其原因是新证书生成后,旧证书没有删…...

《Linux从小白到高手》理论篇:文件权限控制及文件操作相关的命令
List item 本篇介绍Linux文件权限控制及文件操作相关的命令,看完本文,有关Linux文件权限控制及文件操作相关的常用命令你就掌握了99%了。 文件权限 在介绍文件权限之前先来复习下Linux的文件类型,始终记住那句话:Linux系统下&a…...

前端框架React的详细的学习方法和过程
学习React作为前端架构的一部分,是一个系统且逐步深入的过程。以下是一个详细的学习方法和过程,可以帮助你有效地掌握React: 1. 理解React的基础知识 首先,你需要了解React的基本概念,包括它是什么、为什么使用它以及…...

linux中缓存,在kafka上应用总结
linux中的缓存 页缓存 pagecatch(读缓存用于提供快速读)块缓存(用于提供其他设备快速写)当对读缓存读的时候,修改了读的数据,页缓存就会被标记为脏数据,等到写的时候它会向块缓存同步数据&…...

前端练习小项目 —— 让图片变得更 “色”
前言:相信读者在学习完了HTML、CSS和JavaScript之后已经想要迫不及待的想找一个小型的项目来练练手,那么这篇文章就正好能满足你的 “需求”。 ✨✨✨这里是秋刀鱼不做梦的BLOG ✨✨✨想要了解更多内容可以访问我的主页秋刀鱼不做梦-CSDN博客 在开始学习…...

时间卷积网络(TCN)原理+代码详解
目录 一、TCN原理1.1 因果卷积(Causal Convolution)1.2 扩张卷积(Dilated Convolution) 二、代码实现2.1 Chomp1d 模块2.2 TemporalBlock 模块2.3 TemporalConvNet 模块2.4 完整代码示例 参考文献 在理解 TCN 的原理之前ÿ…...

零散的知识
1.物化 在SQL中,物化(Materialization)是指将查询结果保存为物理数据结构以供后续使用的过程。这与普通的视图或查询不同,物化视图会存储查询的结果,而不是每次查询时都动态地重新计算数据。 ①物化视图 物化视图是一…...

Python读取pdf中的文字与表格
一、PyPDF2包安装 在Python中安装PyPDF2库,您可以使用pip包管理器。打开您的命令行工具(例如CMD、Terminal或Anaconda Prompt),然后输入以下命令: pip install PyPDF2 如果您使用的是Python 3,并且系统中…...

【MySQL 08】复合查询
目录 1.准备工作 2.多表查询 笛卡尔积 多表查询案例 3. 自连接 4.子查询 1.单行子查询 2.多行子查询 3.多列子查询 4.在from子句中使用子查询 5.合并查询 1.union 2.union all 1.准备工作 如下三个表,将作为示例,理解复合查询 EMP员工表…...

求1000以内的完数
题目:一个数如果恰好等于他的因子之和(包括1,但不包括这个数),这个数就是完数。编写算法找出1000之内的所有完数,并按下面格式输出其因子:28 its factors are 1,2,4,7,14 代码如下:…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
