蓝桥杯刷题冲刺 | 倒计时8天
作者:指针不指南吗
专栏:蓝桥杯倒计时冲刺🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾
文章目录
- 1.三角形的面积
- 2.图中点的层次
1.三角形的面积
-
题目
链接: 三角形的面积 - 蓝桥云课 (lanqiao.cn)
平面直角坐标系中有一个三角形, 请你求出它的面积。
输入描述
第一行输入一个 T ,代表测试数据量
每组测试数据输入有三行,每行一个实数坐标 (x,y) 代表三角形三个顶点。
1≤T≤10310^3103 ,−10510^5105≤x,y≤10510^5105
输出描述
输出一个实数表示三角形面积。结果保留2位小数,误差不超过 10−210^{-2}10−2
输入输出样例
示例 1
输入
2 0 1 1 0 1 1 0 0 1 1 2 2输出
0.50 0.00 -
第一次 AC 100% 坐标公式
#include<bits/stdc++.h> using namespace std;int main() {int n;cin>>n;double x1,y1,x2,y2,x3,y3;double S;while(n--){cin>>x1>>y1>>x2>>y2>>x3>>y3; //公式背过S=fabs(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2)*1.0/2; //这里,abs的使用,面积没有负的printf("%.2f\n",S);}return 0;} -
题解二 海伦公式----边长
#include<bits/stdc++.h> using namespace std;int main() {int n;cin>>n;long double x1,y1,x2,y2,x3,y3;long double a,b,c;long double S;while(n--){cin>>x1>>y1>>x2>>y2>>x3>>y3;//算出来 三个边长 long double a=sqrt(pow(x1-x2,2)+pow(y1-y2,2));long double b=sqrt(pow(x1-x3,2)+pow(y1-y3,2));long double c=sqrt(pow(x2-x3,2)+pow(y2-y3,2));//海伦公式 long double p=(a+b+c)/2;S=sqrt(p*(p-a)*(p-b)*(p-c)); //背过printf("%.2Lf\n",S); //这里,输出 Lf}return 0;}double 竟然不能用,使用 long doule 才可以
double占用8个字节,long double占用16个字节,因此long double的精度更高,但也会占用更多的内存空间。
一般使用double就可以满足需求,只有在需要更高精度的计算时才会使用long double。
long double 输出用
%Lf这个题为什么用 long double 记住就行 T-T
-
反思
- 把三角形的公式搞定
- 输出格式,
\n以及有小数点的限制,注意!! - 绝对值 整数时,使用 abs;浮点数,使用 fabs
- 上述两种方法,一个边长,一个坐标,应该解决三角形面积就够了
2.图中点的层次
-
题目
链接: 847. 图中点的层次 - AcWing题库
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环。
所有边的长度都是 1,点的编号为 1∼n。
请你求出 1 号点到 n 号点的最短距离,如果从 1 号点无法走到 n 号点,输出 −1。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 a 和 b,表示存在一条从 a 走到 b 的长度为 1 的边。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
数据范围
1≤n,m≤10510^5105
输入样例:
4 5 1 2 2 3 3 4 1 3 1 4输出样例:
1 -
第一次 AC 100%
#include<bits/stdc++.h> using namespace std;const int N=1e5+10;int n,m; int h[N],e[N],ne[N],idx; int d[N];void add(int a,int b) {e[idx]=b,ne[idx]=h[a],h[a]=idx++; }int bfs() {memset(d,-1,sizeof d);d[1]=0;queue<int> q;q.push(1);while(q.size()){int t=q.front();q.pop();for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]==-1){d[j]=d[t]+1;q.push(j);}}}return d[n]; }int main() {cin>>n>>m;memset(h,-1,sizeof h); //!!!!!!!!!! 记得写上while(m--){int a,b;cin>>a>>b;add(a,b);}cout<<bfs();return 0; } -
反思
写一道模板题水一下,不定时复习暴搜
使用邻接表的时候 h 初始化 + add ,初始化别丢

相关文章:

蓝桥杯刷题冲刺 | 倒计时8天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.三角形的面积2.图中点的层次1.三角形的面积 题目 链接: 三角形的面积 - 蓝桥云课 …...

四.JAVA基础面试题:重要知识
四.JAVA基础面试题:重要知识 1.为什么JAVA只有值传递 2.JAVA获取运行时类的四种方式 四.JAVA基础面试题:重要知识 1.为什么JAVA只有值传递 实参:传递给形参的实际参数。 形参:接受实参的参数。值传递:方法接受实参…...

某面试官分享经验:看求职者第一眼,开口说第一句话,面试结果就差不多定了,准确率高达90%以上...
我们以前分享过许多经验,但大多是站在打工人的视角上,今天给大家带来一个面试官的经验:1. 看求职者第一眼,开口说第一句话,面试结果就差不多定了,准确率高达90%以上。2. 绝不考八股文,如果问技术…...

Java开发 - 消息队列之RabbitMQ初体验
目录 前言 RabbitMQ 什么是RabbitMQ RabbitMQ特点 安装启动 RabbitMQ和Kafka的消息收发区别 RabbitMQ使用案例 添加依赖 添加配置 创建RabbitMQ配置类 RabbitMQ消息的发送 RabbitMQ消息的接收 测试 结语 前言 前一篇,我们学习了Kafka的基本使用&#…...
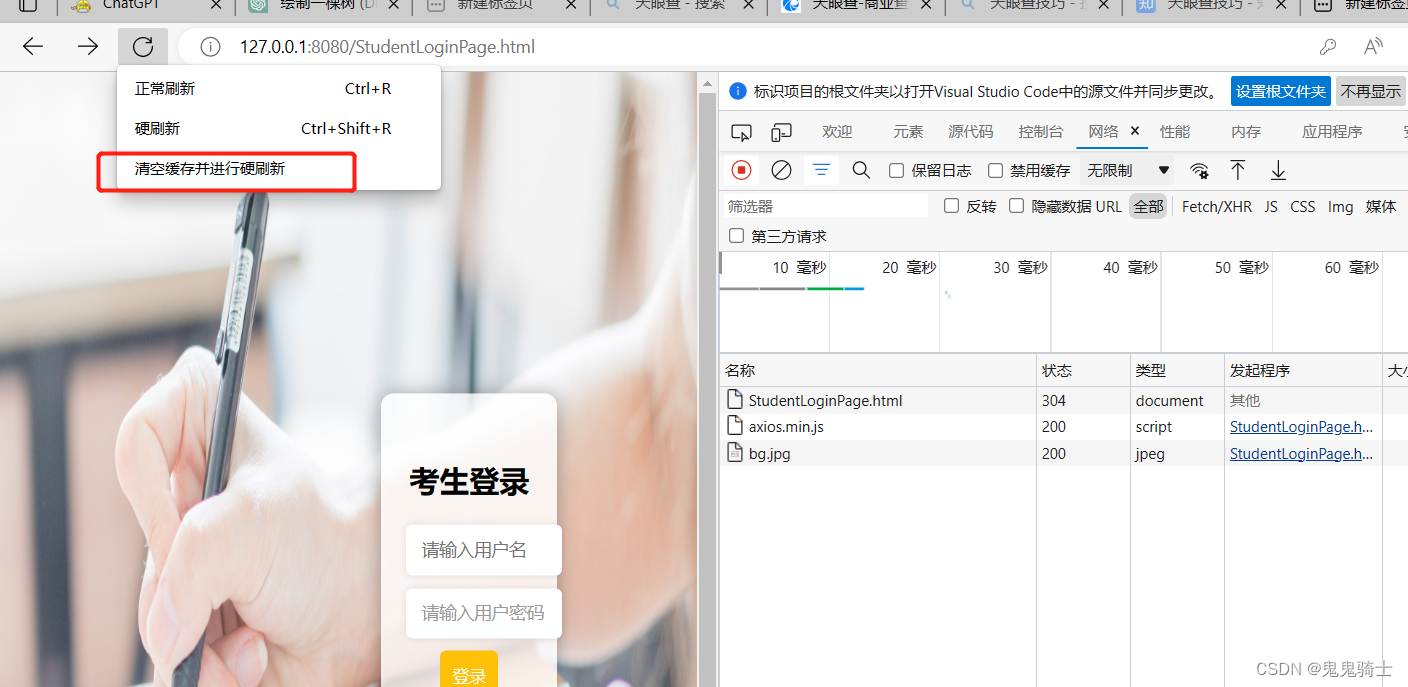
蓝桥杯入职项目(HTML + springBoot)
文章目录需要解决npm包安装axioshttp-servedebug开发下个阶段测试运行方式注意清理磁盘缓存问题解决HTML Web项目的结构通常是基于MVC(Model-View-Controller)模式设计的。下面是一般的项目结构:index.html:项目的入口文件&#x…...

【IAR工程】STM8S208RB基于ST标准库下按键检测
【IAR工程】STM8S208RB基于ST标准库下按键检测📍相关篇《【IAR工程】STM8S208RB基于ST标准库下GPIO点灯示例》🎈《【IAR工程】STM8S208RB基于ST标准库下EXTI外部中断》🔖基于ST STM8S/A标准外设库:STSW-STM8069,版本号:2.3.1&…...
)
【5】深度学习之Pytorch——如何使用张量处理文本数据集(语料库数据集)
在计算机领域,不断崛起的两个领域,一个是CV一个是NLP,下面我们可以探索一下深度学习在NLP的应用和特点。 深度学习在自然语言处理(NLP)领域有广泛的应用。以下是一些主要的应用和特点: 语音识别࿱…...

《Spring系列》第5章 refresh()
前言 Spring框架中最重要的肯定是IOC容器,那么其如何进行初始化,就是通过refresh()这个方法,无论是单独使用Spring框架,还是SpringBoot,最终都会通过执行到这个方法,那么下面会介绍一下这个方法 一、IOC容…...
ThreeJS-缩放、旋转(四)
代码: <template> <div id"three_div"> </div> </template> <script> import * as THREE from "three"; import {OrbitControls } from three/examples/jsm/controls/OrbitControls export default { name: &quo…...

数据更新 | CnOpenData法拍房数据
法拍房数据 一、数据简介 法拍房,即“法院拍卖房产”,是被法院强制执行拍卖的房屋 。当债务人(业主)无力履行借款合约或无法清偿债务时,而被债权人经司法程序向法院申请强制执行,将债务人名下房屋拍卖&…...
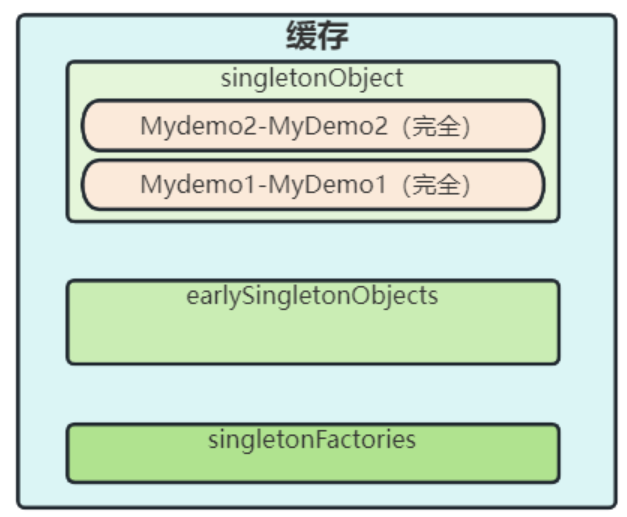
【Spring从成神到升仙系列 五】从根上剖析 Spring 循环依赖
👏作者简介:大家好,我是爱敲代码的小黄,独角兽企业的Java开发工程师,CSDN博客专家,阿里云专家博主📕系列专栏:Java设计模式、数据结构和算法、Kafka从入门到成神、Kafka从成神到升仙…...

设计模式之代理模式(C++)
作者:翟天保Steven 版权声明:著作权归作者所有,商业转载请联系作者获得授权,非商业转载请注明出处 一、代理模式是什么? 代理模式是一种结构型的软件设计模式,在不改变原代码前提下,提供一个代理…...
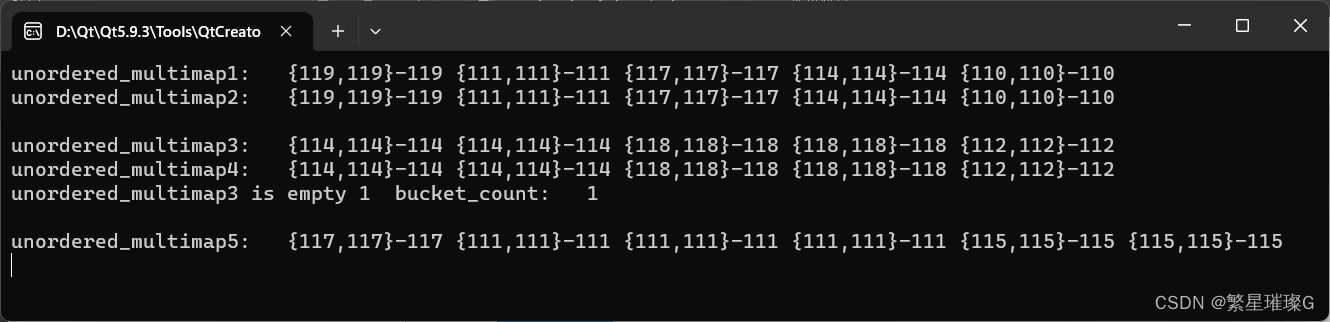
c++11 标准模板(STL)(std::unordered_multimap)(三)
定义于头文件 <unordered_map> template< class Key, class T, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator< std::pair<const Key, T> > > class unordered…...

Linux进程控制-2
紧接着上篇博客出发,我们接着来讲述Linux中进程控制的内容。 目录 1.等待 1.1具体操作 1.等待 进程等待主要的作用在于:父进程创建子进程之后,等待子进程退出,获取子进程的退出码,释放子进程的资源,避…...

快速排序算法
一:快速排序思想 假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数,待会你就知道它用来做啥的了)。为了方便ÿ…...
)
中华好诗词大学季第二季(四)
第七期 1,二十四友一朝尽,爱妾坠楼何足言出自许浑的《金谷园》,“爱妾”指的是谁 2,李白在《九月十日即事》借菊花表达自己的惋惜之情,请问九月十日是什么节日 A 后登高 B 菊花节 C 小重阳 3,贾宝玉在大观园里面题了“曲径通幽”…...

分布式系统容灾部署方案
本文主要以OceanBase部署来说明分布式系统容灾部署方案 分布式系统提供持续可用的服务尤为重要。 好的分布式系统根据需求提供不同等级的的高可用与容灾级别。 而在分布式系统中,数据库系统又是最核心最关键的系统。 我们以数据库分布式系统为主,考虑…...

Python 爬虫性能相关总结
这里我们通过请求网页例子来一步步理解爬虫性能 当我们有一个列表存放了一些url需要我们获取相关数据,我们首先想到的是循环 简单的循环串行 这一种方法相对来说是最慢的,因为一个一个循环,耗时是最长的,是所有的时间总和 代码…...
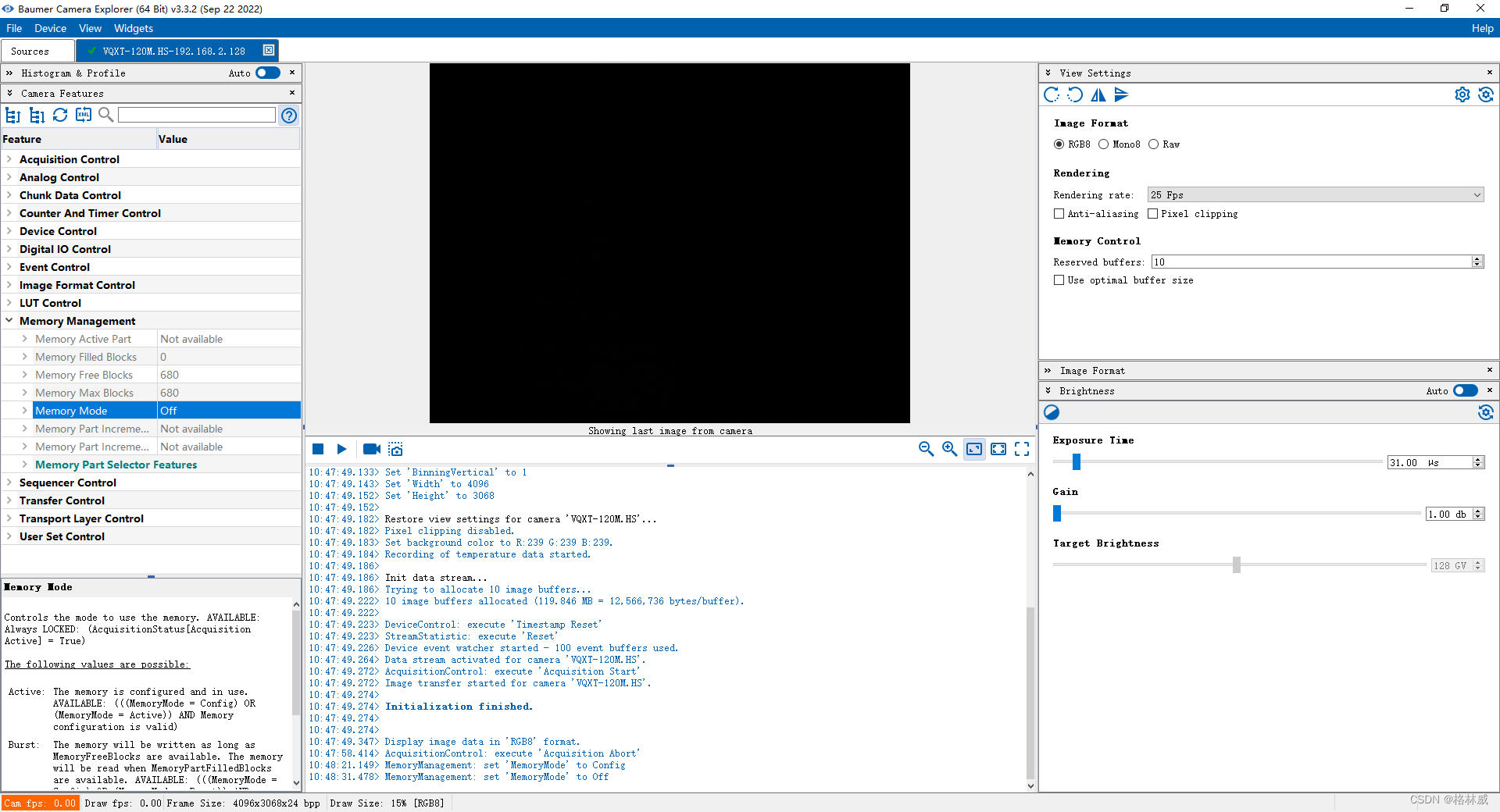
Baumer工业相机堡盟工业相机如何设置网口的IP地址(工业相机连接的网口设置IP地址步骤)
Baumer工业相机堡盟工业相机如何设置网口的IP地址(工业相机连接的网口设置IP地址步骤)Baumer工业相机Baumer工业相机设置网络端口IP地址匹配设置网络端口IP地址和工业相机IP地址匹配第一次打开CameraExplorer软件确认问题为IP地址不匹配问题打开网络连接…...

Android MediaCodec设置H264 Profile到High
H264 High Profile压缩率高,能降低码率,这里记录下MediaCodec Profile设置到High遇到的一些问题。 Android 4.1 就引入了MediaCodecInfo.CodecProfileLevel类,下面截取H264(AVC)的Profile和Level定义: /** Copyright (C) 2012 The Android O…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
