理解无监督学习、无监督图像分割
系列文章目录
文章目录
- 系列文章目录
- 一、无监督学习如何学习 能不能举一个非常具体的例子,带着运算过程的例子
- 总结
- 二、在图像分割中呢,具体怎样实现无监督
- 示例:使用自编码器和k-means进行无监督图像分割
- 1. **数据准备**
- 2. **构建自编码器**
- 3. **训练自编码器**
- 4. **提取特征**
- 5. **k-means聚类**
- 6. **生成分割结果**
- 7. **后处理**
- 示例代码(伪代码)
一、无监督学习如何学习 能不能举一个非常具体的例子,带着运算过程的例子
当然可以!下面我们将通过一个具体的无监督学习示例,使用k-means聚类算法来说明无监督学习的过程,包括数据准备、算法步骤和计算过程。


总结
通过k-means聚类算法,我们成功地将数据点分成了两个聚类,尽管没有任何标签。这一过程展示了无监督学习如何通过数据本身的结构进行学习和分类。每一次迭代中,算法通过计算距离和更新质心来逐步优化聚类结果。
二、在图像分割中呢,具体怎样实现无监督
在图像分割中实现无监督学习可以通过多种方法。以下是一个具体的示例,使用自编码器(Autoencoder)和k-means聚类来进行无监督图像分割的过程。
示例:使用自编码器和k-means进行无监督图像分割
1. 数据准备
假设我们有一组图像数据集,例如医学图像或自然图像。我们将使用这些图像进行无监督分割。
2. 构建自编码器
自编码器是一种神经网络,旨在学习输入数据的压缩表示。它由两个部分组成:
- 编码器:将输入图像压缩成低维表示(潜在空间)。
- 解码器:将低维表示还原为原始图像。
网络结构示例:
- 输入层:图像(例如,256x256x3的RGB图像)
- 编码层:多个卷积层,最后连接到一个全连接层,输出潜在表示(例如,64维向量)
- 解码层:多个反卷积层,将潜在表示还原为原始图像尺寸
3. 训练自编码器
使用重构损失来训练自编码器:
Loss = 1 N ∑ i = 1 N ∥ x i − x ^ i ∥ 2 \text{Loss} = \frac{1}{N} \sum_{i=1}^{N} \| x_i - \hat{x}_i \|^2 Loss=N1∑i=1N∥xi−x^i∥2
这里, x i x_i xi是真实图像, x ^ i \hat{x}_i x^i是重构图像, N N N是图像总数。
4. 提取特征
训练完成后,使用编码器部分提取图像的潜在表示。对于每个输入图像,获得一个64维的特征向量。
5. k-means聚类
对提取的特征进行k-means聚类:
- 选择k值:根据图像内容选择聚类数,例如2(前景和背景)或更多。
- 初始化质心:随机选择k个特征向量作为初始质心。
- 分配步骤:计算每个特征向量到质心的距离,并将其分配到最近的质心。
- 更新步骤:计算新的质心为每个聚类的特征向量均值。
6. 生成分割结果
- 根据k-means的聚类结果,将每个图像的像素分配到对应的聚类,生成分割图。
7. 后处理
- 可以应用形态学操作(如开运算、闭运算)来平滑分割结果,去除小噪声。
示例代码(伪代码)
以下是一个伪代码示例,展示如何实现上述步骤:
import numpy as np
from keras.models import Model
from keras.layers import Input, Conv2D, Flatten, Dense, Reshape, Conv2DTranspose
from sklearn.cluster import KMeans# Step 1: Prepare your dataset (images)
images = load_images() # Load your dataset# Step 2: Build the autoencoder
input_img = Input(shape=(256, 256, 3))
x = Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
x = Conv2D(64, (3, 3), activation='relu', padding='same')(x)
flat = Flatten()(x)
encoded = Dense(64, activation='relu')(flat)# Decoder
x = Dense(64 * 256 * 256, activation='relu')(encoded)
x = Reshape((256, 256, 64))(x)
x = Conv2DTranspose(64, (3, 3), activation='relu', padding='same')(x)
decoded = Conv2DTranspose(3, (3, 3), activation='sigmoid', padding='same')(x)autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='mse')# Step 3: Train the autoencoder
autoencoder.fit(images, images, epochs=50, batch_size=32)# Step 4: Extract features
encoder = Model(input_img, encoded)
features = encoder.predict(images)# Step 5: Perform k-means clustering
kmeans = KMeans(n_clusters=2)
kmeans.fit(features)
labels = kmeans.labels_# Step 6: Generate segmentation masks
segmented_images = generate_masks(labels, images.shape) # Convert labels to masks# Step 7: Post-processing (optional)
segmented_images = post_process(segmented_images)
相关文章:

理解无监督学习、无监督图像分割
系列文章目录 文章目录 系列文章目录一、无监督学习如何学习 能不能举一个非常具体的例子,带着运算过程的例子总结 二、在图像分割中呢,具体怎样实现无监督示例:使用自编码器和k-means进行无监督图像分割1. **数据准备**2. **构建自编码器**3…...

C语言— exec系列函数
exec系列函数 在C语言编程中,exec 系列函数用于在当前进程中执行一个新程序,从而替换当前进程的映像。这些函数不会返回,除非发生错误。exec 系列函数有多个变体,其中最常用的包括 execl, execle, execlp, execv, execve, execvp…...
命名管道Linux
管道是 毫不相关的进程进程间通信::命名管道 管道 首先自己要用用户层缓冲区,还得把用户层缓冲区拷贝到管道里,(从键盘里输入数据到用户层缓冲区里面),然后用户层缓冲区通过系统调用(write)写…...
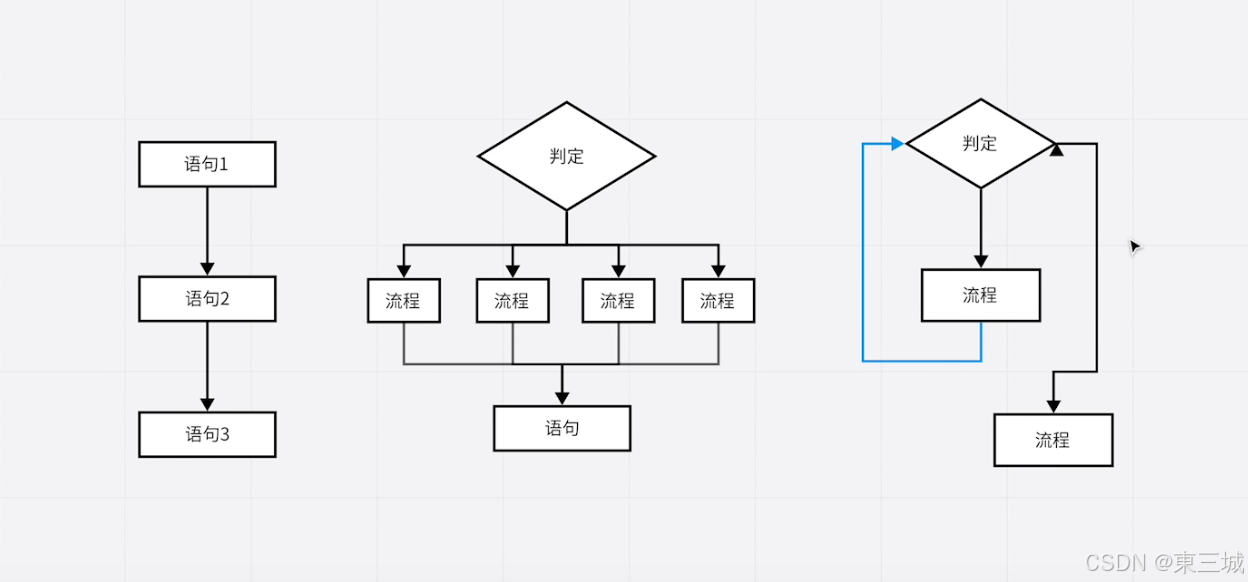
【ios】---swift开发从入门到放弃
swift开发从入门到放弃 环境swift入门变量与常量类型安全和类型推断print函数字符串整数双精度布尔运算符数组集合set字典区间元祖可选类型循环语句条件语句switch语句函数枚举类型闭包数组方法结构体 环境 1.在App Store下载Xcode 2.新建项目(可以先使用这个&…...
【AUTOSAR 基础软件】PduR模块详解(通信路由)
文章包含了AUTOSAR基础软件(BSW)中PduR模块相关的内容详解。本文从AUTOSAR规范解析,ISOLAR-AB配置以及模块相关代码分析三个维度来帮读者清晰的认识和了解PduR这一基础软件模块。文中涉及的ISOLAR-AB配置以及模块相关代码都是依托于ETAS提供的…...

[控制理论]—差分变换法与双线性变换法的基本原理和代码实现
差分变换法与双线性变换法的基本原理和代码实现 1.差分变换法 差分变换法就是把微分方程中的导数用有限差分来近似等效,得到一个与原微分方程逼近的差分方程。 差分变换法包括后向差分与前向差分。 1.1 后向差分法 差分变换如下: d e ( t ) d t e…...
【JavaEE】——多线程常用类
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 引入: 一:Callable和FutureTask类 1:对比Runnable 2:…...
Cilium-Multi Networking-多网络)
Cilium-实战系列-(二)Cilium-Multi Networking-多网络
一、Cilium必要开启的功能 1、enable-multi-network 2、ipam模式选择:multi-pool 二、涉及的CRD资源 1、 ciliumpodippools.cilium.io *通过Cilium管理节点上的pod cidr.网络分为主网络和第二网络。 *主网络的 ciliumpodippools.cilium.io default根据配置文件默认生成的。 …...
springboot自动配置
自动配置的核心就在SpringBootApplication注解上,SpringBootApplication这个注解 底层包含了3个注解,分别是: SpringBootConfiguration ComponentScan EnableAutoConfiguration EnableAutoConfiguration这个注解才是自动配置的核心,它 封…...

mock数据,不使用springboot的单元测试
业务代码 package com.haier.configure.service.impl;import com.baomidou.mybatisplus.core.toolkit.Wrappers; import com.baomidou.mybatisplus.extension.service.impl.ServiceImpl; import com.haier.common.util.RequestUtil; import com.haier.configure.entity.Langua…...
【pytorch】pytorch入门5:最大池化层(Pooling layers )
文章目录 前言一、定义概念 缩写二、参数三、最大池化操作四、使用步骤总结参考文献 前言 使用 B站小土堆课程 一、定义概念 缩写 池化(Pooling)是深度学习中常用的一种操作,用于降低卷积神经网络(CNN)或循环神经网…...

职场上的人情世故,你知多少?这五点一定要了解
职场是一个由人组成的复杂社交网络,人情世故在其中起着至关重要的作用。良好的人际关系可以帮助我们更好地融入团队,提升工作效率,甚至影响职业发展。在职场中,我们需要了解一些关键要素,以更好地处理人际关系…...

Python | Leetcode Python题解之第456题132模式
题目: 题解: class Solution:def find132pattern(self, nums: List[int]) -> bool:candidate_i, candidate_j [-nums[0]], [-nums[0]]for v in nums[1:]:idx_i bisect.bisect_right(candidate_i, -v)idx_j bisect.bisect_left(candidate_j, -v)if…...

【重学 MySQL】五十四、整型数据类型
【重学 MySQL】五十四、整型数据类型 整型类型TINYINTSMALLINTMEDIUMINTINT(或INTEGER)BIGINT 可选属性UNSIGNEDZEROFILL显示宽度(M)AUTO_INCREMENT注意事项 适合场景TINYINTSMALLINTMEDIUMINTINT(或INTEGER࿰…...

查看 Git 对象存储中的内容
查看 Git 对象存储中的内容 ls -C .git/objects/<dir>ls: 列出目录内容的命令。-C: 以列的形式显示内容。.git/objects/<dir>: .git 是存储仓库信息的 Git 目录,objects 是其中存储对象的子目录。<dir> 是对象存储目录下的一个特定的子目录。 此…...

Redis 中热 Key 的判定及其解决方案
引言 Redis 作为高效的内存数据库,常用于缓存、消息队列等场景。随着数据量和并发量的增加,某些数据的访问频率会远远高于其他数据,这些被频繁访问的 Key 被称为 热 Key。热 Key 问题是 Redis 应用中常见的性能瓶颈之一,它可能导…...

elasticsearch创建索引
1对比关系型数据库,创建索引就等同于创建数据库 在postman中,向ES服务器发PUT请求 显示已经创建成功了 http://192.168.1.108:9200/shopping 请求方式get http://192.168.1.108:9200/shopping 请求全部的index的url地址 get 请求 http://192.168.1.10…...

【STM32单片机_(HAL库)】4-2-1【定时器TIM】定时器输出PWM实现呼吸灯实验
1.硬件 STM32单片机最小系统LED灯模块 2.软件 pwm驱动文件添加定时器HAL驱动层文件添加GPIO常用函数定时器输出PWM配置步骤main.c程序 #include "sys.h" #include "delay.h" #include "led.h" #include "pwm.h"int main(void) {HA…...

计算机网络:物理层 —— 信道复用技术
文章目录 信道信道复用技术信道复用技术的作用基本原理常用的信道复用技术频分复用 FDM时分复用 TDM波分复用 WDM码分复用 CDM码片向量基本原理 信道 信道是指信息传输的通道或介质。在通信中,信道扮演着传输信息的媒介的角色,将发送方发送的信号传递给…...

期权懂|期权交易涨跌幅限制会随时调整吗?
本期让我懂 你就懂的期权懂带大家来了解,期权交易涨跌幅限制会随时调整吗?有兴趣的朋友可以看一下。期权小懂每日分享期权知识,帮助期权新手及时有效地掌握即市趋势与新资讯! 期权交易涨跌幅限制会随时调整吗? 涨跌幅…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...
