力扣随机题
最接近原点的K个点
题目
973. 最接近原点的 K 个点 - 力扣(LeetCode)
思路
这就是一道排序题,直接根据公式排序,然后返回对应范围的数组就行了
代码
public int[][] kClosest(int[][] points, int k) {Arrays.sort(points, new Comparator<int[]>() {@Overridepublic int compare(int[] o1, int[] o2) {return ((o1[0]*o1[0]+o1[1]*o1[1])-(o2[0]*o2[0]+o2[1]*o2[1]));}});return Arrays.copyOfRange(points,0,k);}和为K的最少斐波那契数字数目
题目
1414. 和为 K 的最少斐波那契数字数目 - 力扣(LeetCode)
思路
首先用三个变量模拟斐波那契数列,当数列最大值大于k时终止模拟
遍历集合,从最大值开始,就可以找到最少的数目
代码
public int findMinFibonacciNumbers(int k) {List<Integer> list = new ArrayList<>();int a=1;int b=1;while(a+b<=k){int c=a+b;list.add(c);a=b;b=c;}int sum = 0;for(int i=list.size()-1;i>=0&&k>0;i--){int t = list.get(i);if(k>=t){sum++;k=k-t;}}return sum;}相关文章:

力扣随机题
最接近原点的K个点 题目 973. 最接近原点的 K 个点 - 力扣(LeetCode) 思路 这就是一道排序题,直接根据公式排序,然后返回对应范围的数组就行了 代码 public int[][] kClosest(int[][] points, int k) {Arrays.sort(points, n…...

CSS样式基础样式选择器(案例+代码实现+效果图)
目录 1.css样式的规则 2.引入css样式的方式 1)行内式 2)内嵌式 3)外链式 1-link导入 2-import导入 4)总 3.css基础选择器 1)标签选择器 案例:使用标签选择器编写一个圆 1.代码 2.效果 2)类选择器 案例:使用类选择器为div添加背景色 1.代码 2.效果 3)id…...
)
Linux系统编程—I/O缓冲区(C语言实现)
I/O缓冲区 进程的I/O缓冲区机制是计算机操作系统中一个重要的概念,它涉及到数据在内存和外设之间的传输。以下是关于进程的I/O缓冲区机制的详细解释: 1.定义与作用 定义:I/O缓冲区是指在内存里开辟的一块区域,用来存放接收用户输…...

MySQL多表查询:行子查询
先看我的表数据 dept表 emp表 行子查询 子查询返回的结果是一行(可以是多列), 这种子查询称为行子查询 常用的操作符: , <>, IN, NOT IN 例子1. 查询与“张无忌” 的薪资及直属领导相同的员工信息 拆解成两个问题 a. 查询"张无忌"…...

.NET CORE程序发布IIS后报错误 500.19
发布IIS后浏览时报错误500.19,同时配置文件web.config的路径中也存在问号“?”。 可能原因:没有安装运行时...

Qt 6 相比 Qt 5 的主要提升与更新
自从 Qt 6 发布以来,作为 Qt 框架的一个重大版本更新,它在多个核心方面进行了深度优化和改进。与 Qt 5 相比,Qt 6 不仅提升了性能,还改进了对现代硬件和图形 API 的支持,并增强了开发者的工作流程。本文将详细介绍 Qt …...

【数据结构】介绍
介绍数据结构 数据结构是计算机科学中重要的概念,是指组织和管理数据的方式。它涉及到数据的存储、操作和访问等操作。数据结构可以分为线性结构、树形结构和图形结构等。 线性结构是最简单的数据结构之一(本玄也是这样觉得(* ̄▽ ̄*))&#…...

论医疗类系统全国运营推广策略
一、线上推广 搜索引擎优化(SEO)- 重点策略 持续更新网站内容,包括系统功能介绍、成功案例、行业新闻等,提高网站的权重和流量。进行搜索引擎优化(SEO),确定与医疗机构辅助系统相关的关键词&a…...

Redis入门第一步:认识Redis与快速安装配置
认识Redis与快速安装配置🍃 Redis是什么🐲 1.Redis的背景🎍 Redis(Remote Dictionary Server)译为"远程字典服务",它是一款基于内存实现的键值型 NoSQL 数据库, 通常也被称为数据结…...

ES postman操作全量修改,局部修改,删除
全量修改 修改需要调用的url 地址是http://192.168.1.108:9200/shopping/_doc/1001,调用方法使用put 只修改指定的需求的内容的请求方式 post方式就是局部修改 http://192.168.1.108:9200/shopping/_update/1001,请求方式post 上图是只修改id 为1001数…...

社区交流礼仪 | 提问的艺术
唠唠闲话 2021 年通过 Julia 社区了解到开源,自此开始融入开源社区,学习和体验这种独特的协作模式与交流文化,受益良多。本篇文章为开源新手必读,文章中探讨的交流模式,不仅对参与开源项目的协作有所帮助,…...

极客兔兔Gee-Cache Day5
HTTPPool 既可以是服务端,也可以是客户端,这取决于特定的使用场景和上下文: 作为客户端:当本地缓存没有找到需要的数据时,HTTPPool 需要作为客户端,通过 httpGetter (实现了 PeerGetter 接口&am…...
【IPv6】IPv6地址格式及地址分类(组播、单播、任播)整理
IPv6地址格式 IPv6 地址从 IPv4 地址的 32 bits 扩展到 128 bits,IPv6 地址的表示、书写方式也从 IPv4 的点分十进制,修改16进制的冒号分割 IPv4 点分格式(.) 192.168.11.11 IPv6 冒号分割(:) 2408:8459:3032:0000:0000:0000:0001:a9fd IPv6 的规范…...

Linux数据备份
1、Linux服务器中哪些数据需要备份 1)Linux系统重要数据: ①/root/目录,管理员家目录 ②/home/目录,普通用户家目录 ③/etc/目录 ,系统重要的配置文件保存目录 2)安装服务的数据:例apache①…...

回到原点再出发
原文What Goes Around Comes Around作者Michael Stonebraker & Joseph M. Hellerstein其他译文https://zhuanlan.zhihu.com/p/111322429 1. 摘要 本文总结了近35年来的数据模型方案,分成9个不同的时代,讨论了每个时代的方案。我们指出,…...

SimpleFoc以及SVPWM学习补充记录
SimpleFoc SimpleFOC移植STM32(一)—— 简介 FOC控制的过程是这样的: 对电机三相电流进行采样得到 Ia,Ib,Ic。将 Ia,Ib,Ic 经过Clark变换得到 I_alpha I_beta。将 I_alpha I_beta 经过Park变换得到 Id,Iq。计算 Id,Iq 和其设定值 Id_ref 和…...

免费 Oracle 各版本 离线帮助使用和介绍
文章目录 Oracle 各版本 离线帮助使用和介绍概要在线帮助下载离线文档包:解压离线文档:访问离线文档:导航使用:目录介绍Install and Upgrade(安装和升级):Administration(管理&#…...

刷题 二叉树
二叉树的核心思想 - 递归 - 将问题分解为子问题 题型 递归遍历迭代遍历层序遍历 bfs:队列各种递归题目:将问题分解为子问题二叉搜索树 - 中序遍历是递增序列 TreeNode* &prev 指针树形dp 面试经典 150 题 - 二叉树 104. 二叉树的最大深度 广度优…...
操作系统 | 学习笔记 | 王道 | 4.1 文件系统基础
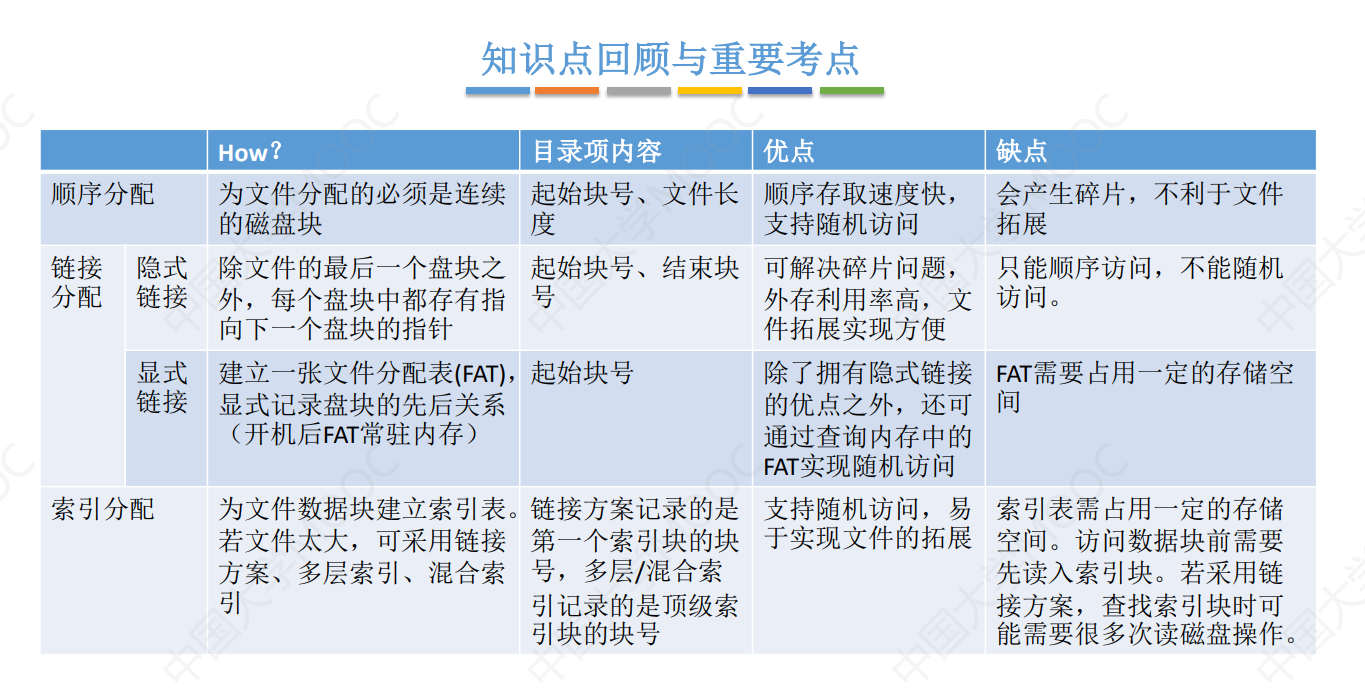
4.文件管理 4.1 文件系统基础 4.1.1 文件的基本概念 定义 文件是以计算机硬盘为载体的存储在计算机上的信息集合,在用户进行的输入、输出中,以文件位基本单位。 文件管理系统是实现的文件的访问、修改和保存,对文件维护管理的系统。 文件的…...

var let const 之间的区别
在JavaScript中,var、let 和 const 是用于声明变量的三种关键字。它们之间有几个重要的区别: 1. 作用域 var: 声明的变量具有函数作用域,即在整个函数内都可以访问。如果在代码块内(如if或for)使用var,该…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
