刷题 二叉树
二叉树的核心思想 - 递归 - 将问题分解为子问题
题型
- 递归遍历
- 迭代遍历
- 层序遍历 bfs:
队列 - 各种递归题目:
将问题分解为子问题 - 二叉搜索树 -
中序遍历是递增序列TreeNode* &prev指针 - 树形dp
面试经典 150 题 - 二叉树
104. 二叉树的最大深度

广度优先遍历
class Solution {
public:// 广度优先遍历int maxDepth(TreeNode* root) {if (root == nullptr) return 0;queue<TreeNode*> que;que.push(root);int result = 0;while (!que.empty()) {++result;int num = que.size();while (num--) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);}}return result;}
};
递归
最大深度 = 1 + max(左子树最大深度, 右子树最大深度)
class Solution {
public:// 递归:最大深度 = 1 + max(左子树最大深度, 右子树最大深度)int maxDepth(TreeNode* root) {if (root == nullptr) return 0;return 1 + max(maxDepth(root->left), maxDepth(root->right));}
};
100. 相同的树

递归
树相同 --> 根节点相同 + 左子树相同 + 右子树相同
class Solution {
public:// 递归// 树相同 --> 根节点相同 + 左子树相同 + 右子树相同bool isSameTree(TreeNode* p, TreeNode* q) {if (p == nullptr && q == nullptr) {return true;} else if (p == nullptr || q == nullptr) {return false;}if (p->val != q->val) {return false;}if (isSameTree(p->left, q->left) == false) {return false;}if (isSameTree(p->right, q->right) == false) {return false;}return true;}
};
226. 翻转二叉树

递归
class Solution {
public:// 翻转二叉树 --> // 根节点的左子树 = 将右子树进行反转// 根节点的右子树 = 将左子树进行反转TreeNode *invertTree(TreeNode *root) {if (root == nullptr) return nullptr;auto left = invertTree(root->left); // 翻转左子树auto right = invertTree(root->right); // 翻转右子树root->left = right; // 交换左右儿子root->right = left;return root;}
};
⭐️⭐️112. 路径总和

回溯
class Solution {
public:// 回溯bool backtracking(TreeNode* root, int path_sum, int targetSum) { if (root == nullptr) return false;if (root->right == nullptr && root->left == nullptr) { // 到达叶子节点,终止回溯return (path_sum + root->val == targetSum);}return (backtracking(root->left, path_sum + root->val, targetSum) || \backtracking(root->right, path_sum + root->val, targetSum));}bool hasPathSum(TreeNode* root, int targetSum) {return backtracking(root, 0, targetSum);}
};
⭐️⭐️迭代
class Solution {
public:// 递归: 树 存在和为 targetSum// 也即左子树存在和为 targetSum - root->val 或者 右子树存在和为 targetSum - root->valbool hasPathSum(TreeNode* root, int targetSum) {if (root == nullptr) return false;if (root->left == nullptr && root->right == nullptr) {return (targetSum == root->val); } return (hasPathSum(root->left, targetSum - root->val) || \hasPathSum(root->right, targetSum - root->val));}
};
层序遍历
比较简单,不做讨论
面试经典 150 题 - 二叉树层次遍历
199. 二叉树的右视图
class Solution {
public:vector<int> rightSideView(TreeNode* root) {if (root == nullptr) return vector<int>{};queue<TreeNode*> que;que.push(root);vector<int> result;while (!que.empty()) {size_t n = que.size();for (size_t i = 0; i < n; ++i) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);if (i == n - 1) result.push_back(cur->val);}}return result;}
};
637. 二叉树的层平均值
class Solution {
public:vector<double> averageOfLevels(TreeNode* root) {if (root == nullptr) return vector<double>{};queue<TreeNode*> que;que.push(root);vector<double> result;while (!que.empty()) {size_t n = que.size();double sum = 0.0;for (size_t i = 0; i < n; ++i) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);sum += cur->val;}result.push_back(sum / n);}return result;}
};
[102. 二叉树的层序遍历
](https://leetcode.cn/problems/binary-tree-level-order-traversal/?envType=study-plan-v2&envId=top-interview-150)
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {if (root == nullptr) return vector<vector<int>>{};queue<TreeNode*> que;que.push(root);vector<vector<int>> result;while (!que.empty()) {size_t n = que.size();vector<int> layer(n, 0);for (size_t i = 0; i < n; ++i) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);layer[i] = cur->val;}result.push_back(layer);}return result;}
};
103. 二叉树的锯齿形层序遍历 - 写入的时候改一下索引即可

class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {if (root == nullptr) return vector<vector<int>>{};queue<TreeNode*> que;que.push(root);vector<vector<int>> result;bool to_right = false;while (!que.empty()) {to_right = !to_right;size_t n = que.size();vector<int> layer(n, 0);for (size_t i = 0; i < n; ++i) {TreeNode* cur = que.front();que.pop();if (cur->left) que.push(cur->left);if (cur->right) que.push(cur->right);if (to_right) {layer[i] = cur->val;} else {layer[n - 1 - i] = cur->val;}}result.push_back(layer);}return result;}
};面试经典 150 题 - 二叉搜索树 - ⭐️TreeNode*& prev⭐️ - 中序遍历有序
98. 验证二叉搜索树
class Solution {
public:bool traversal(TreeNode* root, TreeNode*& prev) {if (root == nullptr) return true;if (!traversal(root->left, prev)) return false;if (prev != nullptr && prev->val >= root->val) return false;prev = root;return traversal(root->right, prev);}bool isValidBST(TreeNode* root) {TreeNode* prev = nullptr;return traversal(root, prev);}
};
530. 二叉搜索树的最小绝对差

使用数组暂存
class Solution {
public:// 二叉搜索树的特征:左子树 < 根节点 < 右子树// 中序遍历即可获得最小差值void traversal(TreeNode* root, vector<int>& vals, int& min_diff) {if (root == nullptr) return;traversal(root->left, vals, min_diff);if (!vals.empty()) min_diff = min(min_diff, root->val - vals.back()); vals.push_back(root->val);traversal(root->right, vals, min_diff);}int getMinimumDifference(TreeNode* root) {vector<int> vals;int min_diff = INT_MAX;traversal(root, vals, min_diff);return min_diff;}
};
⭐️优化 - 使用一个 prev_val 即可
class Solution {
public:// 二叉搜索树的特征:左子树 < 根节点 < 右子树// 中序遍历即可获得最小差值// 如果不想使用数组暂存的话就需要存储一个 prev 指针void traversal(TreeNode* root, TreeNode*& prev, int& min_diff) {if (root == nullptr) return;traversal(root->left, prev, min_diff);if (prev != nullptr) min_diff = min(min_diff, root->val - prev->val); prev = root;traversal(root->right, prev, min_diff);}int getMinimumDifference(TreeNode* root) {int min_diff = INT_MAX;TreeNode* prev = nullptr;traversal(root, prev, min_diff);return min_diff;}
};
230. 二叉搜索树中第 K 小的元素 - 想象用数组存储元素 - 实际只使用索引即可 - 注意终止条件
class Solution {
public:void traversal(TreeNode* root, int& val, int& count, int k) {if (root == nullptr || count >= k) return; // 递归终止条件traversal(root->left, val, count, k);++count; // 如果用数组存储元素,想象这里是数组的第 count 个数字(从0开始)if (count == k) {val = root->val;return;}traversal(root->right, val, count, k);}int kthSmallest(TreeNode* root, int k) {int val, count = 0;traversal(root, val, count, k);return val;}
};
相关文章:

刷题 二叉树
二叉树的核心思想 - 递归 - 将问题分解为子问题 题型 递归遍历迭代遍历层序遍历 bfs:队列各种递归题目:将问题分解为子问题二叉搜索树 - 中序遍历是递增序列 TreeNode* &prev 指针树形dp 面试经典 150 题 - 二叉树 104. 二叉树的最大深度 广度优…...
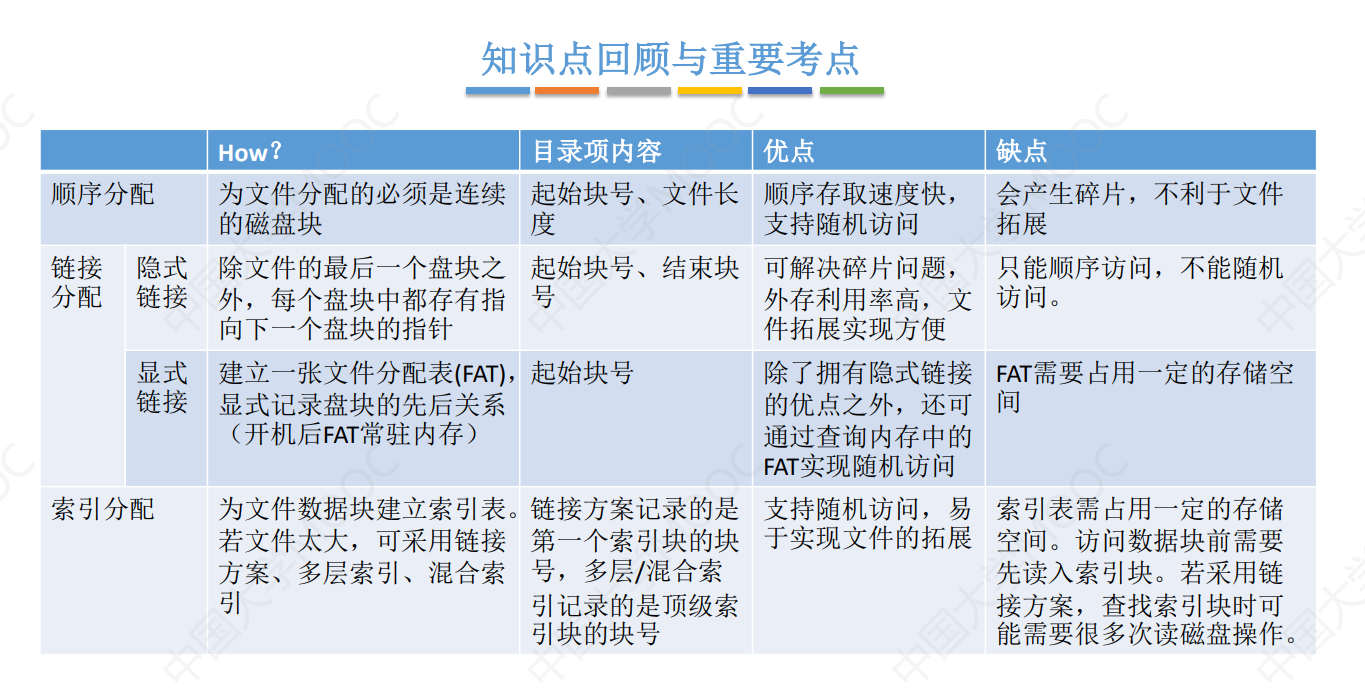
操作系统 | 学习笔记 | 王道 | 4.1 文件系统基础
4.文件管理 4.1 文件系统基础 4.1.1 文件的基本概念 定义 文件是以计算机硬盘为载体的存储在计算机上的信息集合,在用户进行的输入、输出中,以文件位基本单位。 文件管理系统是实现的文件的访问、修改和保存,对文件维护管理的系统。 文件的…...

var let const 之间的区别
在JavaScript中,var、let 和 const 是用于声明变量的三种关键字。它们之间有几个重要的区别: 1. 作用域 var: 声明的变量具有函数作用域,即在整个函数内都可以访问。如果在代码块内(如if或for)使用var,该…...

【springboot】简易模块化开发项目整合Swagger2
接上一项目【springboot】简易模块化开发项目整合MyBatis-plus,进行拓展项目 1.新建模块 右键项目→New→Module,新建一个模块 父项目选择fast-demo,命名为fast-demo-config,用于存放所有配置项 添加后,项目结构如图…...

【Linux第五课-进程概念下】环境变量、程序地址空间
目录 环境变量main参数 --- 命令行参数环境变量环境变量特性 --- 命令行操作main函数的参数获取环境变量environ获取环境变量getenv()获取环境变量unset移除本地变量或环境变量set显示本地变量 代码获取和设置环境变量 本地变量 程序地址空间什么是进程地址空间为什么有地址空间…...
)
mysql学习教程,从入门到精通,SQL 临时表(37)
1、SQL 临时表 在SQL中,临时表(Temporary Table)是一种在会话或连接期间临时存储数据的表。它们对于存储中间结果、简化复杂查询以及提高性能非常有用。以下是一个创建和使用临时表的示例。 假设我们有一个名为 employees 的表,…...

算法闭关修炼百题计划(四)
仅供个人复习 1.两数相加2.寻找峰值6.岛屿的最大面积3.最大数4.会议室5.最长连续序列6.寻找两个正序数组的中位数 1.两数相加 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 请…...
)
头歌实践教学平台 大数据编程 实训答案(二)
第三阶段 Spark算子综合案例 Spark算子综合案例 - JAVA篇 第1关:WordCount - 词频统计 任务描述 本关任务:使用 Spark Core 知识编写一个词频统计程序。 相关知识 略 编程要求 请仔细阅读右侧代码,根据方法内的提示,在Begin - End区域内进行代码补充,具体任务如下: …...
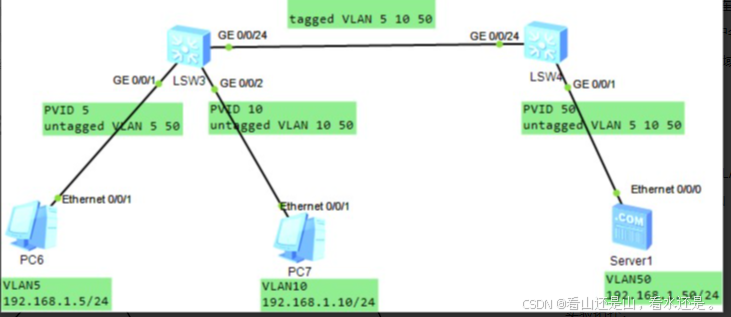
路由交换实验指南
案例 01:部署使用 eNSP 平台实验需求: 安装华为 eNSP 网络模拟平台打开 eNSP 平台,新建拓扑并绘制网络能够成功启动交换机、计算机设备 实验步骤: 安装华为 eNSP 网络模拟平台启动安装程序 配置安装内容 防护墙允许 eNSP 程序的…...

了解网页 blob 链接
blob 链接 自从 HTML5 提供了 video 标签,在网页中播放视频变得非常简单,只要在代码中插入一个 video 标签,再将 video 标签的 src 属性设置为视频的链接就可以了。由于 src 指向的是视频文件真实的地址,所以当我们通过浏览器的调…...
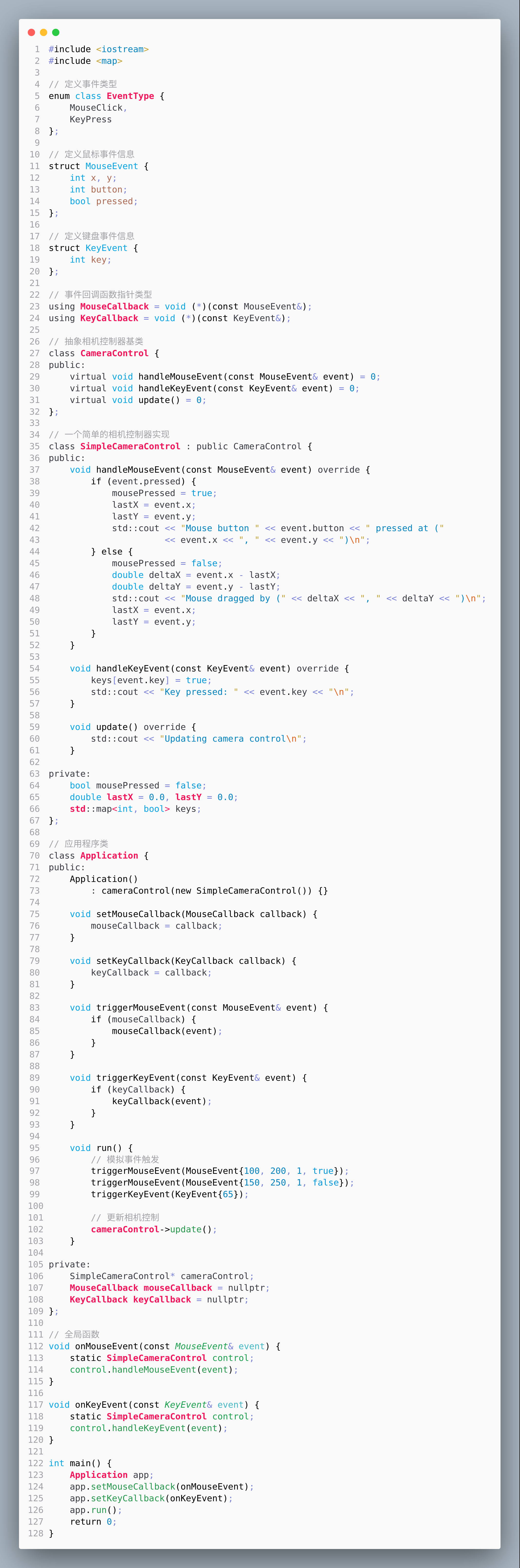
OpenGL笔记之事件驱动设计将相机控制类和应用程序类分离
OpenGL笔记之事件驱动设计将相机控制类和应用程序类分离 —— 2024-10-02 下午 bilibili赵新政老师的教程看后笔记 code review! 文章目录 OpenGL笔记之事件驱动设计将相机控制类和应用程序类分离1.代码图片2.分析3.UML4.代码 1.代码图片 运行 Mouse button 1 pressed at (1…...

低代码时代的企业信息化:规范与标准化的重要性
在当今数字化转型的浪潮中,企业的信息化建设正逐步向低代码平台倾斜。低代码不仅仅是简化开发过程,更是对企业内部流程、规范和标准化的深刻理解与应用。本文将探讨低代码在企业信息化中的重要性,特别是在运维和开发流程中的标准化࿰…...

理解无监督学习、无监督图像分割
系列文章目录 文章目录 系列文章目录一、无监督学习如何学习 能不能举一个非常具体的例子,带着运算过程的例子总结 二、在图像分割中呢,具体怎样实现无监督示例:使用自编码器和k-means进行无监督图像分割1. **数据准备**2. **构建自编码器**3…...

C语言— exec系列函数
exec系列函数 在C语言编程中,exec 系列函数用于在当前进程中执行一个新程序,从而替换当前进程的映像。这些函数不会返回,除非发生错误。exec 系列函数有多个变体,其中最常用的包括 execl, execle, execlp, execv, execve, execvp…...
命名管道Linux
管道是 毫不相关的进程进程间通信::命名管道 管道 首先自己要用用户层缓冲区,还得把用户层缓冲区拷贝到管道里,(从键盘里输入数据到用户层缓冲区里面),然后用户层缓冲区通过系统调用(write)写…...
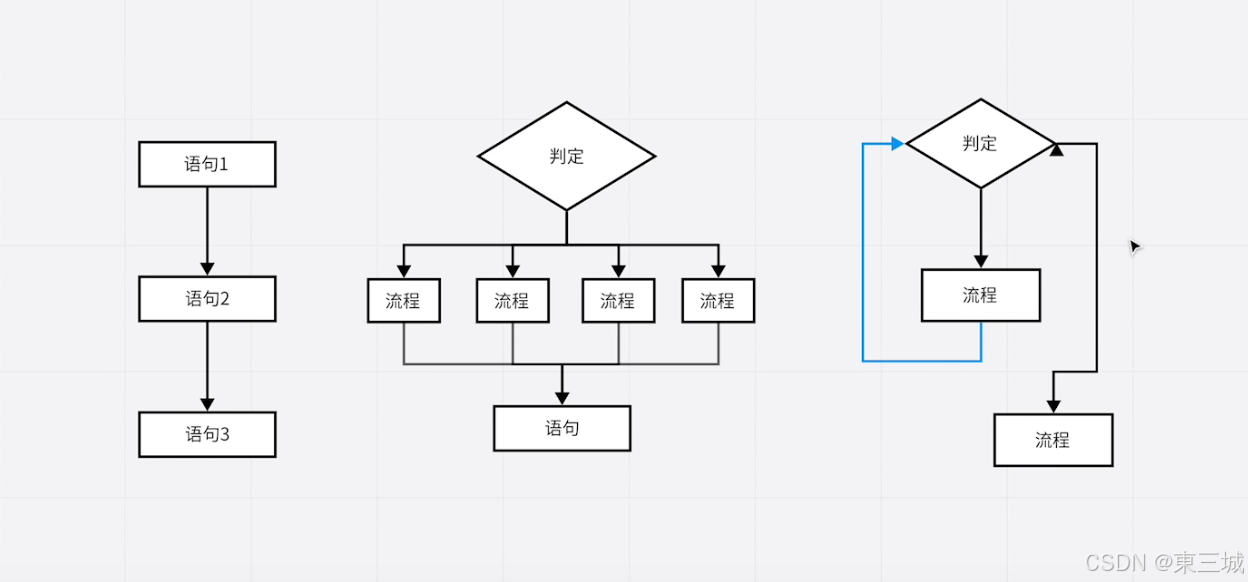
【ios】---swift开发从入门到放弃
swift开发从入门到放弃 环境swift入门变量与常量类型安全和类型推断print函数字符串整数双精度布尔运算符数组集合set字典区间元祖可选类型循环语句条件语句switch语句函数枚举类型闭包数组方法结构体 环境 1.在App Store下载Xcode 2.新建项目(可以先使用这个&…...
【AUTOSAR 基础软件】PduR模块详解(通信路由)
文章包含了AUTOSAR基础软件(BSW)中PduR模块相关的内容详解。本文从AUTOSAR规范解析,ISOLAR-AB配置以及模块相关代码分析三个维度来帮读者清晰的认识和了解PduR这一基础软件模块。文中涉及的ISOLAR-AB配置以及模块相关代码都是依托于ETAS提供的…...

[控制理论]—差分变换法与双线性变换法的基本原理和代码实现
差分变换法与双线性变换法的基本原理和代码实现 1.差分变换法 差分变换法就是把微分方程中的导数用有限差分来近似等效,得到一个与原微分方程逼近的差分方程。 差分变换法包括后向差分与前向差分。 1.1 后向差分法 差分变换如下: d e ( t ) d t e…...
【JavaEE】——多线程常用类
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 引入: 一:Callable和FutureTask类 1:对比Runnable 2:…...
Cilium-Multi Networking-多网络)
Cilium-实战系列-(二)Cilium-Multi Networking-多网络
一、Cilium必要开启的功能 1、enable-multi-network 2、ipam模式选择:multi-pool 二、涉及的CRD资源 1、 ciliumpodippools.cilium.io *通过Cilium管理节点上的pod cidr.网络分为主网络和第二网络。 *主网络的 ciliumpodippools.cilium.io default根据配置文件默认生成的。 …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
