算法闭关修炼百题计划(四)
仅供个人复习
- 1.两数相加
- 2.寻找峰值
- 6.岛屿的最大面积
- 3.最大数
- 4.会议室
- 5.最长连续序列
- 6.寻找两个正序数组的中位数
1.两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
/*
因为两个链表都是逆序,相当于个位数在最前面,所以可以直接相加,多余的十位数、百位数 用 temp 记录下来,加到下一个节点
*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {//构建新链表的头节点和尾节点ListNode* head = nullptr;ListNode* tail = nullptr;int tmp = 0; //相加的进位,比如7+8=15,tmp=1while (l1 != nullptr || l2 != nullptr) {int val1 = l1 != nullptr ? l1->val : 0; // l1不为空,取节点的值,为空则取0int val2 = l2 != nullptr ? l2->val : 0;int sum = val1 + val2 + tmp;// 往相加的链表后拼接节点if (head == nullptr) {head = new ListNode(sum % 10);tail = head;} else {tail->next = new ListNode(sum % 10);tail = tail->next;}tmp = sum / 10; //除了个位数,剩下的是进位,放入tmpif (l1 != nullptr) l1 = l1->next;if (l2 != nullptr) l2 = l2->next;}//最后如果 tmp ≠ 0,说明还有进位,需要一个节点存放if (tmp > 0) tail->next = new ListNode(tmp);return head;}
};
2.寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
二分法,注意mid+1可能越界
class Solution {
public:int findPeakElement(vector<int>& nums) {int L = -1, R = nums.size();if(nums.size() == 1) return 0;while(L + 1 != R){int mid = (L + R) / 2;if(mid == nums.size() - 1){R = nums.size() - 1;break;}if(nums[mid] > nums[mid + 1]) R = mid;else L = mid;}return R;}
};
6.岛屿的最大面积
class Solution {
public:int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};int count;void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y){for(int i = 0; i < 4; i ++){int nextx = x + dir[i][0];int nexty = y + dir[i][1];if(nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;if(!visited[nextx][nexty] && grid[nextx][nexty] == 1){visited[nextx][nexty] = true;count++;dfs(grid, visited, nextx, nexty);}}}int maxAreaOfIsland(vector<vector<int>>& grid) {int res = 0;vector<vector<bool>> visited(grid.size(), vector<bool>(grid[0].size(), false));for(int i = 0; i < grid.size(); i ++){for(int j = 0; j < grid[0].size(); j ++){if(grid[i][j] == 1 && !visited[i][j]){count = 1;//每个岛屿重置countvisited[i][j] = true;dfs(grid, visited, i, j);res = max(res, count);}}}return res;}};
3.最大数
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
class Solution {
public:string largestNumber(vector<int>& nums) {vector<string> str;for(auto i : nums){str.push_back(to_string(i));}auto cmp = [](string left, string right){return left + right > right + left;};sort(str.begin(), str.end(), cmp);string ans = "";for(auto c : str){ans += c;}if(ans[0] == '0') return "0";return ans;}
};
4.会议室
给你一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,返回 所需会议室的最小数量 。
输入:intervals = [[0,30],[5,10],[15,20]]
输出:2
可以把他理解为上车下车问题
同时在车上最多人数就是需要的会议室数量

挺巧的这个做法
class Solution {
public:int minMeetingRooms(vector<vector<int>>& intervals) {map<int, int> umap;for(auto it : intervals){umap[it[0]]++;umap[it[1]]--;}int ans = 0, cnt = 0;for(auto itt : umap){cnt += itt.second;ans = max(ans, cnt);}return ans;}
};
用map而不是unordered_map,因为键值对在map中是有序的,即元素按照键的升序排列。用他才能用上车下车的写法。
5.最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> set(nums.begin(), nums.end());int res = 0;for(int num : set){if(set.find(num - 1) != set.end()) continue;//不是第一个就跳过,因为我们要找第一个int curNum = num;int curLen = 1;while(set.find(curNum + 1) != set.end()){curNum += 1;curLen += 1;}res = max(res, curLen);}return res;}
};
6.寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
碎碎念:除了学然后背还能怎样呢?这篇已经接近终章了,最后应该到不了一百题,剩余不多的时间给自己复习吧,反正都是背,学了没背住就太亏了。
有难度,但可能是因为题解看多了,看懂并不难。。。(笑
简单点来说,要找第k小的,咱每次排除k / 2个元素,两个有序数组,分别找他们的第k/2 - 1个数,比较,较小的那个数所在的数字的第0~k/2-1个数都不可能是答案,所以就排除掉了,这个数字的index++,另一个数组的index怎么办?
首先明确,咱不断比较的是有可能存在答案的数组的前k/2 - 1,没被排除的数组,从下标0开始都有可能,他们的index,仍然是+ k/2 - 1,从index开始的
其次,注意边界问题,假如数组顺序是完全无缝衔接的,那么就会遇到越界问题,越界的时候说明,中位数在另一个数组中,直接加上剩余的k即可
class Solution {
public:int getKthElement(vector<int>& nums1, vector<int>& nums2, int k){int m = nums1.size();int n = nums2.size();int index1 = 0, index2 = 0;while(true){if(index1 == m) return nums2[index2 + k - 1];if(index2 == n) return nums1[index1 + k - 1];if(k == 1) return min(nums1[index1], nums2[index2]);int newIndex1 = min(index1 + k/2 - 1, m - 1);//防止越界int newIndex2 = min(index2 + k/2 - 1, n - 1);int pivot1 = nums1[newIndex1];int pivot2 = nums2[newIndex2];if(pivot1 <= pivot2){k -= newIndex1 - index1 + 1;index1 = newIndex1 + 1;}else{k -= newIndex2 - index2 + 1;index2 = newIndex2 + 1;}}}double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int totalLength = nums1.size() + nums2.size();if(totalLength % 2 == 1) return getKthElement(nums1, nums2, (totalLength + 1) / 2);else{return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;}}
};
相关文章:

算法闭关修炼百题计划(四)
仅供个人复习 1.两数相加2.寻找峰值6.岛屿的最大面积3.最大数4.会议室5.最长连续序列6.寻找两个正序数组的中位数 1.两数相加 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 请…...
)
头歌实践教学平台 大数据编程 实训答案(二)
第三阶段 Spark算子综合案例 Spark算子综合案例 - JAVA篇 第1关:WordCount - 词频统计 任务描述 本关任务:使用 Spark Core 知识编写一个词频统计程序。 相关知识 略 编程要求 请仔细阅读右侧代码,根据方法内的提示,在Begin - End区域内进行代码补充,具体任务如下: …...
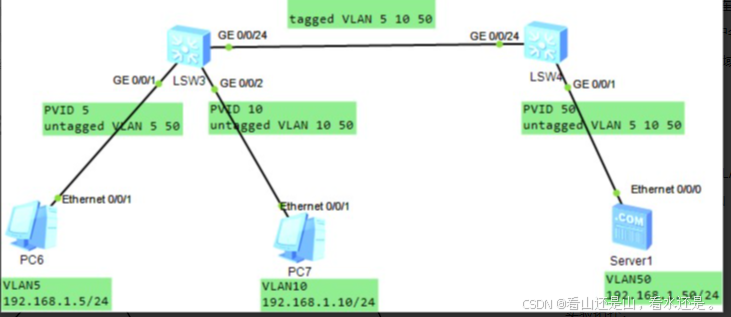
路由交换实验指南
案例 01:部署使用 eNSP 平台实验需求: 安装华为 eNSP 网络模拟平台打开 eNSP 平台,新建拓扑并绘制网络能够成功启动交换机、计算机设备 实验步骤: 安装华为 eNSP 网络模拟平台启动安装程序 配置安装内容 防护墙允许 eNSP 程序的…...

了解网页 blob 链接
blob 链接 自从 HTML5 提供了 video 标签,在网页中播放视频变得非常简单,只要在代码中插入一个 video 标签,再将 video 标签的 src 属性设置为视频的链接就可以了。由于 src 指向的是视频文件真实的地址,所以当我们通过浏览器的调…...
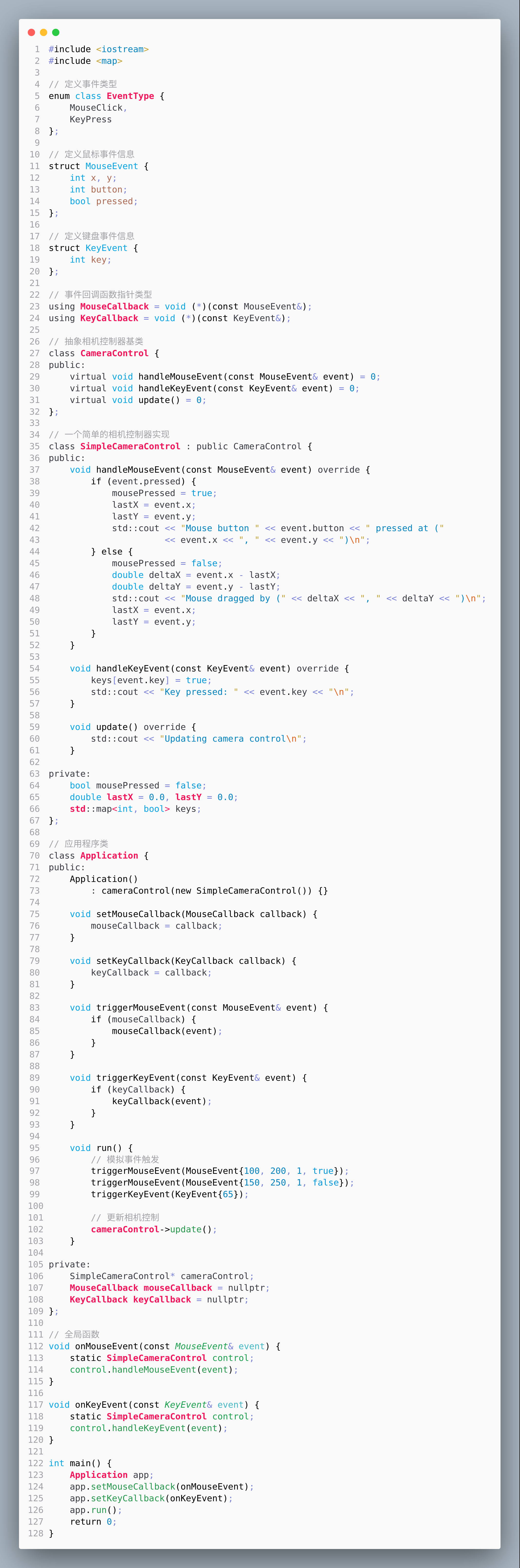
OpenGL笔记之事件驱动设计将相机控制类和应用程序类分离
OpenGL笔记之事件驱动设计将相机控制类和应用程序类分离 —— 2024-10-02 下午 bilibili赵新政老师的教程看后笔记 code review! 文章目录 OpenGL笔记之事件驱动设计将相机控制类和应用程序类分离1.代码图片2.分析3.UML4.代码 1.代码图片 运行 Mouse button 1 pressed at (1…...

低代码时代的企业信息化:规范与标准化的重要性
在当今数字化转型的浪潮中,企业的信息化建设正逐步向低代码平台倾斜。低代码不仅仅是简化开发过程,更是对企业内部流程、规范和标准化的深刻理解与应用。本文将探讨低代码在企业信息化中的重要性,特别是在运维和开发流程中的标准化࿰…...

理解无监督学习、无监督图像分割
系列文章目录 文章目录 系列文章目录一、无监督学习如何学习 能不能举一个非常具体的例子,带着运算过程的例子总结 二、在图像分割中呢,具体怎样实现无监督示例:使用自编码器和k-means进行无监督图像分割1. **数据准备**2. **构建自编码器**3…...

C语言— exec系列函数
exec系列函数 在C语言编程中,exec 系列函数用于在当前进程中执行一个新程序,从而替换当前进程的映像。这些函数不会返回,除非发生错误。exec 系列函数有多个变体,其中最常用的包括 execl, execle, execlp, execv, execve, execvp…...
命名管道Linux
管道是 毫不相关的进程进程间通信::命名管道 管道 首先自己要用用户层缓冲区,还得把用户层缓冲区拷贝到管道里,(从键盘里输入数据到用户层缓冲区里面),然后用户层缓冲区通过系统调用(write)写…...
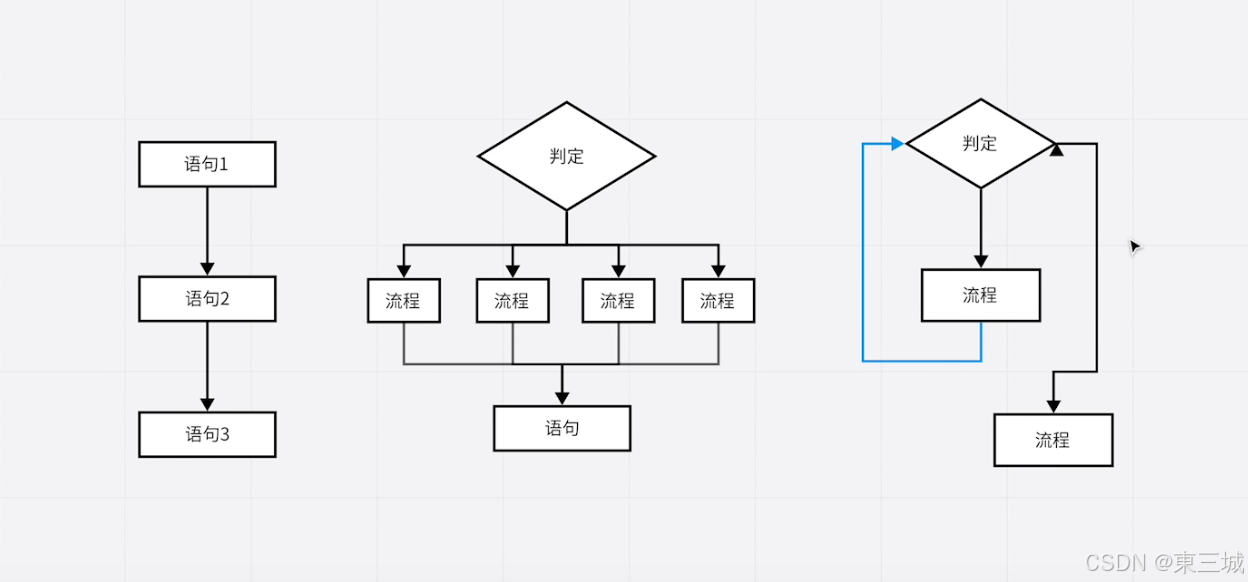
【ios】---swift开发从入门到放弃
swift开发从入门到放弃 环境swift入门变量与常量类型安全和类型推断print函数字符串整数双精度布尔运算符数组集合set字典区间元祖可选类型循环语句条件语句switch语句函数枚举类型闭包数组方法结构体 环境 1.在App Store下载Xcode 2.新建项目(可以先使用这个&…...
【AUTOSAR 基础软件】PduR模块详解(通信路由)
文章包含了AUTOSAR基础软件(BSW)中PduR模块相关的内容详解。本文从AUTOSAR规范解析,ISOLAR-AB配置以及模块相关代码分析三个维度来帮读者清晰的认识和了解PduR这一基础软件模块。文中涉及的ISOLAR-AB配置以及模块相关代码都是依托于ETAS提供的…...

[控制理论]—差分变换法与双线性变换法的基本原理和代码实现
差分变换法与双线性变换法的基本原理和代码实现 1.差分变换法 差分变换法就是把微分方程中的导数用有限差分来近似等效,得到一个与原微分方程逼近的差分方程。 差分变换法包括后向差分与前向差分。 1.1 后向差分法 差分变换如下: d e ( t ) d t e…...
【JavaEE】——多线程常用类
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 引入: 一:Callable和FutureTask类 1:对比Runnable 2:…...
Cilium-Multi Networking-多网络)
Cilium-实战系列-(二)Cilium-Multi Networking-多网络
一、Cilium必要开启的功能 1、enable-multi-network 2、ipam模式选择:multi-pool 二、涉及的CRD资源 1、 ciliumpodippools.cilium.io *通过Cilium管理节点上的pod cidr.网络分为主网络和第二网络。 *主网络的 ciliumpodippools.cilium.io default根据配置文件默认生成的。 …...
springboot自动配置
自动配置的核心就在SpringBootApplication注解上,SpringBootApplication这个注解 底层包含了3个注解,分别是: SpringBootConfiguration ComponentScan EnableAutoConfiguration EnableAutoConfiguration这个注解才是自动配置的核心,它 封…...

mock数据,不使用springboot的单元测试
业务代码 package com.haier.configure.service.impl;import com.baomidou.mybatisplus.core.toolkit.Wrappers; import com.baomidou.mybatisplus.extension.service.impl.ServiceImpl; import com.haier.common.util.RequestUtil; import com.haier.configure.entity.Langua…...
【pytorch】pytorch入门5:最大池化层(Pooling layers )
文章目录 前言一、定义概念 缩写二、参数三、最大池化操作四、使用步骤总结参考文献 前言 使用 B站小土堆课程 一、定义概念 缩写 池化(Pooling)是深度学习中常用的一种操作,用于降低卷积神经网络(CNN)或循环神经网…...

职场上的人情世故,你知多少?这五点一定要了解
职场是一个由人组成的复杂社交网络,人情世故在其中起着至关重要的作用。良好的人际关系可以帮助我们更好地融入团队,提升工作效率,甚至影响职业发展。在职场中,我们需要了解一些关键要素,以更好地处理人际关系…...

Python | Leetcode Python题解之第456题132模式
题目: 题解: class Solution:def find132pattern(self, nums: List[int]) -> bool:candidate_i, candidate_j [-nums[0]], [-nums[0]]for v in nums[1:]:idx_i bisect.bisect_right(candidate_i, -v)idx_j bisect.bisect_left(candidate_j, -v)if…...

【重学 MySQL】五十四、整型数据类型
【重学 MySQL】五十四、整型数据类型 整型类型TINYINTSMALLINTMEDIUMINTINT(或INTEGER)BIGINT 可选属性UNSIGNEDZEROFILL显示宽度(M)AUTO_INCREMENT注意事项 适合场景TINYINTSMALLINTMEDIUMINTINT(或INTEGER࿰…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
