【LeetCode每日一题】——17.电话号码的字母组合
文章目录
- 一【题目类别】
- 二【题目难度】
- 三【题目编号】
- 四【题目描述】
- 五【题目示例】
- 六【题目提示】
- 七【解题思路】
- 八【时间频度】
- 九【代码实现】
- 十【提交结果】
一【题目类别】
- 回溯
二【题目难度】
- 中等
三【题目编号】
- 17.电话号码的字母组合
四【题目描述】
- 给定一个仅包含数字
2-9的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 - 给出数字到字母的映射如下(与电话按键相同)。注意
1不对应任何字母。

五【题目示例】
-
示例 1:
- 输入:digits = “23”
- 输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
-
示例 2:
- 输入:digits = “”
- 输出:[]
-
示例 3:
- 输入:digits = “2”
- 输出:[“a”,“b”,“c”]
六【题目提示】
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
七【解题思路】
- 但凡涉及到组合类的题目,基本都使用回溯算法解决,本题也不例外,不过是在原本的基础上添加映射关系
- 根据题目信息可知,我们最终组合的是字母,但是输入数据为数字,所以需要简历一个数字到字母的映射
- 其余步骤和正常的回溯过程一致
- 设置边界条件:如果所有的数字都遍历完毕了,就完成此次计算
- 回溯拼接某一电话号码对应的字母:和正常的回溯过程一致,不过需要先取出数字对应的字母进行回溯
- 最后返回结果即可
- 具体细节可以参考下面的代码
八【时间频度】
- 时间复杂度: O ( 3 m × 4 n ) O(3^m × 4^n) O(3m×4n), m m m为 3 3 3个字母对应的数字个数, n n n为 4 4 4个字母对应的数字个数
- 空间复杂度: O ( m + n ) O(m + n) O(m+n), m m m为 3 3 3个字母对应的数字个数, n n n为 4 4 4个字母对应的数字个数
九【代码实现】
- Java语言版
class Solution {// 数字和字母的映射private static final String[] phoneMap = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz",};public List<String> letterCombinations(String digits) {// 边界条件的判断if (digits == null || digits.length() == 0) {return new ArrayList<>();}// 存储最终结果List<String> res = new ArrayList<>();// 从第一个电话号码开始计算dfs(res, new StringBuffer(), digits, 0);// 返回最终结算结果return res;}// 使用回溯计算电话号码的字母组合private void dfs(List<String> res, StringBuffer temp, String digits, int index) {// 将所有电话号码遍历完毕即可返回if (index == digits.length()) {res.add(temp.toString());return;}// 回溯拼接某一电话号码对应的字母char digit = digits.charAt(index);String letters = phoneMap[digit - '0'];for (int i = 0; i < letters.length(); i++) {temp.append(letters.charAt(i));dfs(res, temp, digits, index + 1);temp.deleteCharAt(temp.length() - 1);}}}
- Python语言版
class Solution:def letterCombinations(self, digits: str) -> List[str]:# 边界条件的判断if not digits:return list()# 数字和字母的映射phoneMap = {"2" : "abc","3" : "def","4" : "ghi","5" : "jkl","6" : "mno","7" : "pqrs","8" : "tuv","9" : "wxyz",}# 存储最终结果res = list()# 存储临时结果temp = list()# 使用回溯计算电话号码的字母组合def dfs(index):# 将所有电话号码遍历完毕即可返回if index == len(digits):res.append("".join(temp))return# 回溯拼接某一电话号码对应的字母digit = digits[index]for letter in phoneMap[digit]:temp.append(letter)dfs(index + 1)temp.pop()# 从第一个电话号码开始计算dfs(0)# 返回最终结算结果return res
- C++语言版
class Solution {public:// 数字和字母的映射const vector<string> phoneMap = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz",};// 使用回溯计算电话号码的字母组合void dfs(vector<string>& res, string& temp, string digits, int index) {// 将所有电话号码遍历完毕即可返回if (index == digits.size()) {res.push_back(temp);return;}// 回溯拼接某一电话号码对应的字母int digit = digits[index] - '0';const string& letters = phoneMap[digit];for (char letter : letters) {temp.push_back(letter);dfs(res, temp, digits, index + 1);temp.pop_back();}}vector<string> letterCombinations(string digits) {// 存储最终结果vector<string> res;// 边界条件的判断if (digits.empty()) {return res;}// 存储临时结果string temp;// 从第一个电话号码开始计算dfs(res, temp, digits, 0);// 返回最终结算结果return res;}
};
十【提交结果】
-
Java语言版

-
Python语言版

-
C++语言版

相关文章:

【LeetCode每日一题】——17.电话号码的字母组合
文章目录 一【题目类别】二【题目难度】三【题目编号】四【题目描述】五【题目示例】六【题目提示】七【解题思路】八【时间频度】九【代码实现】十【提交结果】 一【题目类别】 回溯 二【题目难度】 中等 三【题目编号】 17.电话号码的字母组合 四【题目描述】 给定一个…...

Git管理远程仓库
添加远程仓库 要新增远程,请在终端上存储存储库的目录中使用 git remote add 命令。 git remote add 命令采用两个参数: 远程名称(例如 origin)远程 URL(例如 https://github.com/OWNER/REPOSITORY.git)…...

在 /var/cache/apt/archives/ 上没有足够的可用空间的解决方法
问题 apt-get upgrade 更新软件包时,提示没有足够的空间。 分析 一般来说,除非下载的文件过于大,整个服务器的内存都不够用,否则可以改变默认的下载路径进行下载。 解决方法 找一个空间足够的目录,新建一个单独的…...

FastAdmin Apache下设置伪静态
FastAdmin Apache下设置伪静态 一、引言 FastAdmin 是一个基于ThinkPHP和Bootstrap框架开发的快速后台开发框架,它以其简洁、高效、易于扩展的特点,广受开发者的喜爱。在部署FastAdmin项目时,为了提高访问速度和用户体验,我们通…...
MPI程序实例:自适应数值积分(主从模式)
目录 一、主从模式的自适应梯形公式 二、串行程序 三、基于非阻塞通信的并行程序 四、基于散发/收集通信的并行程序 上一节我们介绍了采用梯形公式结合自适应局部区间加密,计算一个函数在给定区间上的定积分达到指定精度。 MPI程序实例:自适应数值积分-CSDN博客…...

蓝桥杯—STM32G431RBT6(IIC通信--EEPROM(AT24C02)存储器进行通信)
一、什么是IIC?24C02存储器有什么用? IIC (IIC 是半双工通信总线。半双工意味着数据在某一时刻只能沿一个方向传输,即发送数据的时候不能接收数据,接收数据的时候不能发送数据)即集成电路总线(…...

【重学 MySQL】六十二、非空约束的使用
【重学 MySQL】六十二、非空约束的使用 定义目的关键字特点作用创建非空约束删除非空约束注意事项 在MySQL中,非空约束(NOT NULL Constraint)是一种用于确保表中某列不允许为空值的数据库约束。 定义 非空约束(NOT NULL Constra…...

Python获取json返回的字符串获取方法大全
1、使用 json.loads() 解析JSON字符串 import jsonjson_string {"name": "Alice", "age": 25, "city": "Beijing"} data json.loads(json_string)# 获取字符串值 name data[name] print("Name:", name) # 输…...

FreeBSD14.1 rm命令的疑惑
在/tmp目录发现有很多目录和文件,准备把它们都删除,结果发现都删不掉 这些文件目录如图: /tmp % ls -la total 9143 drwxrwxrwt 421 root wheel 486 10月 8 11:58 . drwxr-xr-x 23 root wheel 32 10月 8 10:06 .. drwx----…...

LSTM模型变种
LSTM模型变种 一、GRU 1.什么是GRU GRU(Gated Recurrent Unit)是一种循环神经网络(RNN)的变体,它被设计用来解决传统RNN在处理长序列时可能遇到的梯度消失或梯度爆炸问题。GRU通过引入门控机制来控制信息的流动&…...
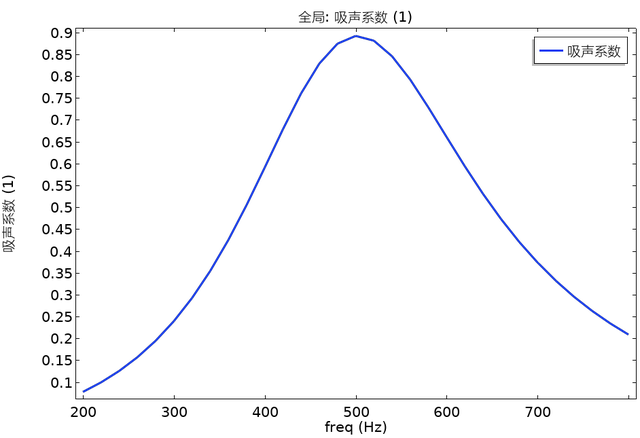
基于comsol模拟微穿孔板和卷曲通道的混合吸声器低频吸声
研究背景: 具有深亚波长厚度(5cm)的吸收器对低频声音(<500Hz)的衰减在噪声控制工程中引起了极大的兴趣。然而,由于低频声音的强穿透性和普通材料的弱固有分散性,这是一项具有挑战性的任务。…...

Ajax ( 是什么、URL、axios、HTTP、快速收集表单 )Day01
AJAX 一、Ajax是什么1.1名词解释1.1.1 服务器1.1.2 同步与异步1. 同步(Synchronous)2. 异步(Asynchronous)3. 异步 vs 同步 场景4. 异步在 Web 开发中的常见应用: 1.2 URL 统一资源定位符1.2.1 URL - 查询参数1.2.2 ax…...

【Java 循环控制实例详解【While do... while】】
Java 循环控制详解【While & do… while】 在 Java 中,循环控制是程序设计中非常重要的部分,主要包括 while 循环和 do...while 循环。本文将详细介绍这两种循环的基本语法、执行流程及相关示例。 1. while 循环控制 基本语法 循环变量初始化; wh…...

10.2 Linux_进程_进程相关函数
创建子进程 函数声明如下: pid_t fork(void); 返回值:失败返回-1,成功返回两次,子进程获得0(系统分配),父进程获得子进程的pid 注意:fork创建子进程,实际上就是将父进程复制一遍作为子进程&…...

栈与队列面试题(Java数据结构)
前言: 这里举两个典型的例子,实际上该类型的面试题是不确定的! 用栈实现队列: 232. 用栈实现队列 - 力扣(LeetCode) 方法一:双栈 思路 将一个栈当作输入栈,用于压入 push 传入的数…...

手撕数据结构 —— 顺序表(C语言讲解)
目录 1.顺序表简介 什么是顺序表 顺序表的分类 2.顺序表的实现 SeqList.h中接口总览 具体实现 顺序表的定义 顺序表的初始化 顺序表的销毁 打印顺序表 编辑 检查顺序表的容量 尾插 尾删 编辑 头插 头删 查找 在pos位置插入元素 删除pos位置的值 …...

女友学习前端第二天-笔记
2024/10/8笔记 表格 table 表格 tr 行 td 单元格内容 th 表头 第一行相当于h1 alignleft /center /right 对齐方式 应在table边上 比如<table alignleft> border 代表边框 也应在table边上 比如<table alignleft border"1"> cellpadding 单元外框与…...

电脑手机下载小米xiaomi redmi刷机包太慢 解决办法
文章目录 修改前下载速度修改后下载速度修改方法(修改host) 修改前下载速度 一开始笔者以为是迅雷没开会员的问题,在淘宝上买了一个临时会员后下载速度依然最高才100KB/s 修改后下载速度 修改方法(修改host) host文…...

Python中的策略模式:解锁编程的新维度
引言 策略模式是一种行为型设计模式,允许算法独立于使用它的客户端而变化。这使得我们可以根据不同的情况选择不同的算法或策略来解决问题,从而增强系统的灵活性。在日常开发中,策略模式常用于处理多种算法或行为之间的切换,比如…...
的概念和使用方法)
ara::core::Future::then()的概念和使用方法
1. 概念 在ara::core::Future的上下文中,then()是一种用于处理异步操作结果的机制。一个Future代表一个尚未完成的异步计算,它最终会产生一个结果或者一个错误。then()方法允许你在Future完成时注册一个回调函数(或者说后续操作)…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
