算法设计-二分
一、有序和单调
二分本质上是一种更加智能的搜索状态空间的方式,他需要状态空间的状态呈现一种“有序的一维数组”的形式,然后再进行搜索。所以一开始的排序是无法避免的。
因为二分的写法问题,所以应当怎样排序也是有一定讲究的,所以排序的时候就可以定义一定的比较方式。
如果更加细致的讨论的话,其实有序只是一个“小条件”,比如说很多枚举、搜索类的题目的状态空间也是有序的,但是我们却没有用二分法,这是因为其核心是,适用于二分法的题目,它的状态和解之间的关系是单调的,如下所示

如左图所示,如果我们对于 mid 有了一个讨论,我们就可以根据需求去选择往左或者往右,右图也是同理,我们知道只要小一点就可以将结果置高,那么最终的结果就会变成“到底小多少”,就是一个很容易解决的问题了。
但是如果状态和结果之间的关系并不单调,那么就无法使用二分法了,如下所示

左图还可以使用“三分法”,但是对于右侧,完全没有办法使用“分法”了,但是不可否认,右图的状态空间也是有序的,没准可以用动态规划求解。
二、二分模板
二分一共有两个模板,这是因为二分的本质不是通过二分找到“唯一适合“的点,二分一般呈现一种“最优化”的特点,它要找到是“符合条件”的最大的或者最小的。我们下面的讨论,都默认状态空间是增序排列的。
这就导致当 mid 符合条件的时候,我们需要判定该往哪一边走了,通常情况下,我们希望找到约束条件下的最大值,那么就应当向 mid 右侧去寻找,而当我们希望找到约束条件下的最小值,那么就应当向 mid 的左侧去寻找。
在寻找更小的区间的时候,有两个原则需要遵守,一个是缩小后的区间一定是包括 mid 的,是不可以跳过 mid 的,这是因为 mid 可能是唯一的“最优值”,所以是不能跳过的;另一个是一定要在 mid 的基础上进行移动,比如说 mid + 1, mid - 1 这样的移动,这是因为在整数中,如果 right - left = 1 而不进行移动,也就是 left = mid, right = mid ,这就会导致死循环的出现。综上所述,我们一般在 mid 符合约束条件的时候,利用的是 left = mid, right = mid 来确保对于 mid 的保留,而当 mid 不符合条件的时候,进行 left = mid + 1, right = mid - 1 的操作来避免死循环。
同时,需要注意二分法的边界条件,这个其实有多种写法,我选择了 left < right 作为循环的条件,那么退出的时候就有 left == mid == right,可以选择任何一个索引作为最终结果。
最后,还需要注意当搜索不到的情况,最后会返回什么,这取决于区间缩小时的移动条件,如果是 left = mid + 1,那么就会导致在 right 暂停,相反,则在 left 暂停。
所以模板如下,对于选择“最小值”,其中 check(int) 函数用于检测是否满足条件:
// 求符合约束的最小值
while (left < right)
{// 向下取整int mid = (left + right) >> 1;// mid 是满足条件的,那么向左侧搜索,包括 midif (check(mid)){right = mid;}// mid 不满足条件,向右侧搜索,那么最可能满足条件的是 mid + 1else {left = mid + 1;}
}
对于选择“最大值”
// 求符合约束的最大值
while (left < right)
{// 向上取整int mid = (left + right + 1) >> 1;// 如果 mid 满足条件,那么向右侧搜索,包括 midif (check(mid)){left = mid;}// mid 不满足条件,向左侧搜索,最有可能满足条件的是 mid - 1else{right = mid - 1;}
}
对比如下
| 条目 | 模板 1 | 模板 2 |
|---|---|---|
| 目标 | 求出满足约束的最小值 | 求出满足约束的最大值 |
mid 取整方式 | 向 left 取整 | 向 right 取整 |
| 搜索为空的返回值 | 状态空间 right | 状态空间 left |
| 跳过方向 | 向右 left = mid + 1 | 向左 right = mid - 1 |
三、STL 算法
与上面提出的模板类似的 stl 算法是 lower_bound() ,它可以返回第一个大于等于某个值的迭代器,也就是这个值的下界位置
// 在 [first, last) 区域内查找不小于 val 的元素
ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,const T& val);
// 在 [first, last) 区域内查找第一个不符合 comp 规则的元素
ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last,const T& val, Compare comp);
还有一个类似的函数是 upper_bound() ,它可以返回第一个大于某个值的迭代器,也就是这个值的上界位置
// 查找[first, last)区域中第一个大于 val 的元素。
ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,const T& val);
// 查找[first, last)区域中第一个不符合 comp 规则的元素
ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last,const T& val, Compare comp);
然后还有一个 equal_range() ,返回的是两个迭代器的 pair,指明了范围
// 找到 [first, last) 范围中所有等于 val 的元素
pair<ForwardIterator,ForwardIterator> equal_range (ForwardIterator first, ForwardIterator last, const T& val);
// 找到 [first, last) 范围内所有等于 val 的元素
pair<ForwardIterator,ForwardIterator> equal_range (ForwardIterator first, ForwardIterator last, const T& val, Compare comp);
最后还有一个 bin_search() ,返回一个布尔值来确定在有序状态空间中是否有特定值
//查找 [first, last) 区域内是否包含 val
bool binary_search (ForwardIterator first, ForwardIterator last,const T& val);
//根据 comp 指定的规则,查找 [first, last) 区域内是否包含 val
bool binary_search (ForwardIterator first, ForwardIterator last,const T& val, Compare comp);
示意图如下
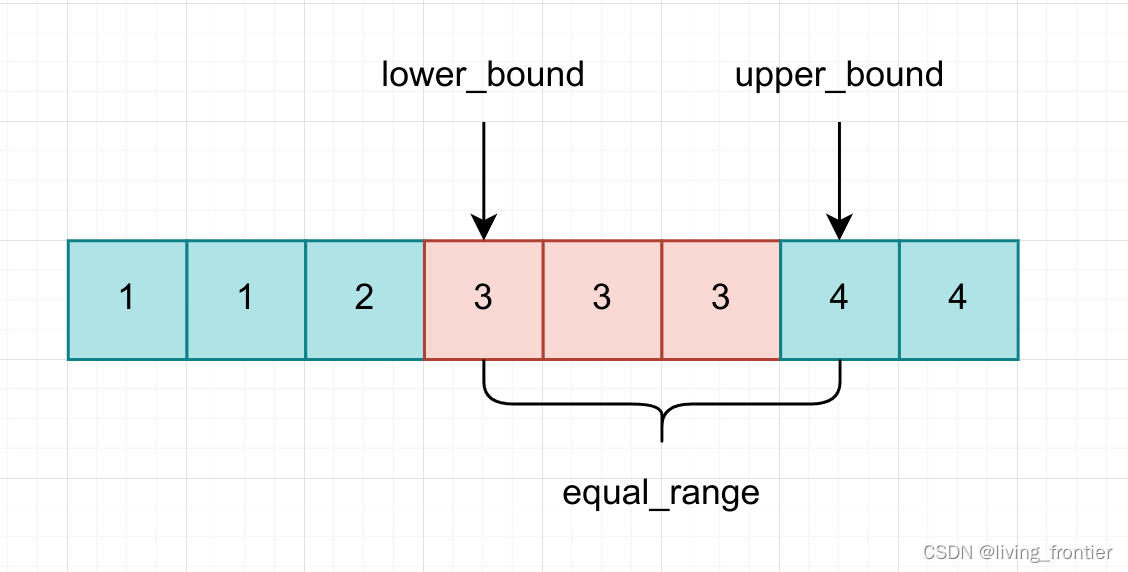
对于 lower_bound() ,其实本质是模板 1 的设计模式,找到的是符合条件的最小值,其代码如下
template <class ForwardIterator, class T> // ForwardIterator 前向迭代器
ForwardIterator lower_bound(ForwardIterator first, ForwardIterator last, const T &val)
{// it 对应 midForwardIterator it;// traits 是萃取机的意思,也就是萃取 iterator 里的信息,并给到算法// count 是搜索区间步长,step 是下一步的步长iterator_traits<ForwardIterator>::difference_type count, step;// count 的初始值就是 first 和 last 的距离(first 对应 left,last 对应 right)count = distance(first, last);// 步长大于 0,与 left < right 相同while (count > 0){it = first;// 二分step = count / 2;// 等价于 mid = left + (right - left) / 2advance(it, step);// 判断 mid 是否满足条件// mid 此时不满足条件if (*it < val) // 或者 if (comp(*it,val)),对应第 2 种语法格式{// first = mid + 1first = ++it;// count 约缩小一半count -= step + 1;}// mid 满足条件,缩小步长(与使用 last 类似)else{count = step;}}return first;
}
因为与模式 1 相似,所以当不存在相似的值的时候,返回的迭代器等于 last 。
upper_bound() 的本质依然是模板 1,因为它寻找的是满足大于搜索值的最小值,所以代码结构与 lower_bound() 相同。
template <class ForwardIterator, class T>
ForwardIterator upper_bound(ForwardIterator first, ForwardIterator last, const T &val)
{ForwardIterator it;iterator_traits<ForwardIterator>::difference_type count, step;count = std::distance(first, last);while (count > 0){it = first;step = count / 2;std::advance(it, step);// 与 lower_bound() 只有这里不同,此时表示 mid 不满足大于的条件if (!(val < *it)) // 或者 if (!comp(val,*it)), 对应第二种语法格式{first = ++it;count -= step + 1;}else{count = step;}}return first;
}
同样的,当不存在相似的值的时候,返回的迭代器等于 last 。
equal_range() 本质就是调用了 lower_bound() 和 upper_bound() ,如下所示
template <class ForwardIterator, class T>
pair<ForwardIterator, ForwardIterator> equal_range(ForwardIterator first, ForwardIterator last, const T &val)
{ForwardIterator it = std::lower_bound(first, last, val);return std::make_pair(it, std::upper_bound(it, last, val));
}
binary_search() 调用了 lower_bound() ,将返回值与 last 比较,并且确定搜索值比最小值(first)小(这是搜索不到的情况)
template <class ForwardIterator, class T>
bool binary_search(ForwardIterator first, ForwardIterator last, const T &val)
{first = std::lower_bound(first, last, val);return (first != last && !(val < *first));
}
四、二分验证法
这是一类固定的题型,一般呈现“最小最大值”这样的特点(并不绝对),其本质是其答案的状态空间呈现很好的线性有序性(说不定就是个 [0,max)[0, max)[0,max) 的区间),我们可以通过二分答案的方法,获得 mid 值,然后利用这个 mid 值去进行模拟验证,如果可以的话,那么就二分继续搜索。
比如说下面的这题
[NOIP2015 提高组] 跳石头
题目描述
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 NNN 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 MMM 块岩石(不能移走起点和终点的岩石)。
输入格式
第一行包含三个整数 L,N,ML,N,ML,N,M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。保证 L≥1L \geq 1L≥1 且 N≥M≥0N \geq M \geq 0N≥M≥0。
接下来 NNN 行,每行一个整数,第 iii 行的整数 Di(0<Di<L)D_i( 0 < D_i < L)Di(0<Di<L), 表示第 iii 块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输出格式
一个整数,即最短跳跃距离的最大值。
样例 #1
样例输入 #1
25 5 2 2 11 14 17 21样例输出 #1
4提示
输入输出样例 1 说明
将与起点距离为 222和 141414 的两个岩石移走后,最短的跳跃距离为 444(从与起点距离 171717 的岩石跳到距离 212121 的岩石,或者从距离 212121 的岩石跳到终点)。
数据规模与约定
对于 20%20\%20%的数据,0≤M≤N≤100 \le M \le N \le 100≤M≤N≤10。
对于 50%50\%50% 的数据,0≤M≤N≤1000 \le M \le N \le 1000≤M≤N≤100。
对于 100%100\%100%的数据,0≤M≤N≤50000,1≤L≤1090 \le M \le N \le 50000,1 \le L \le 10^90≤M≤N≤50000,1≤L≤109。
可以看到这个题目的答案空间是在 [0,L)[0, L)[0,L) 之间的,虽然题目看着很复杂,但是如果考虑用二分的方法去做,对于每一个 mid 值的检验,是很容易进行模拟的,如下所示
#include <bits/stdc++.h>using namespace std;int l, m, n;
int d[50005];// 对于传入的 mid,进行模拟检验
bool check(int step)
{int cnt = 0;int pre = 0;for (int i = 0; i <= n; i++){// 如果距离小于 step,说明需要将这个石头移除if (d[i] - pre < step){cnt++;}// 否则就更新前一个木桩else{pre = d[i];}}// 最终的结果是移除的石头不能多余 mreturn cnt <= m;
}int main()
{cin >> l >> n >> m;for (int i = 0; i < n; i++){cin >> d[i];}d[n] = l;int left = 0, right = l + 1;// 因为是求解最大值,所以采用的是模板 2while (left < right){int mid = (left + right + 1) >> 1;if (check(mid)){left = mid;}else{right = mid - 1;}}cout << left;return 0;
}
需要注意的是,在 check() 中,因为采用的是模拟方法,所以可能会导致复杂度比较高,所以当模拟到失败的时候,需要进行减枝优化。比如说洛谷上的这道题目 https://www.luogu.com.cn/problem/P3853 ,它的格式基本上与前面的题目相同,但是在 check() 上进行减枝
bool check(int step)
{int cnt = 0, pre = 0;for (int i = 0; i < n;){if (d[i] - pre > step){cnt++;pre += step;}else{pre = d[i];i++;}// 减枝if (cnt > m){return false;}}return true;
}
五、实数二分
实数二分的模板要更加容易记忆,唯一需要注意的就是精度问题,因为控制不好精度,很容易导致死循环(似乎到了 1e-7 左右就容易 tle,这可能是由于双精度浮点数的精度相比较大导致的,所以一般采用 1e-6),一定要注意题目中的描述,模板如下
double left = 0, right = 1e10;
while (left + 1e-6 < right)
{double mid = (left + right) / 2;if (check(mid)){left = mid;}else{right = mid;}
}
相关文章:

算法设计-二分
一、有序和单调 二分本质上是一种更加智能的搜索状态空间的方式,他需要状态空间的状态呈现一种“有序的一维数组”的形式,然后再进行搜索。所以一开始的排序是无法避免的。 因为二分的写法问题,所以应当怎样排序也是有一定讲究的&…...
隧道技术基础
隧道技术基础基本概念端口转发应用层代理基本概念 攻击者通过边界主机进入内网,往往会利用它当跳板进行横向渗透,但现在的内部网络大多部署了很多安全设备,网络结构错综复杂,对于某些系统的访问会受到各种阻挠,这就需…...
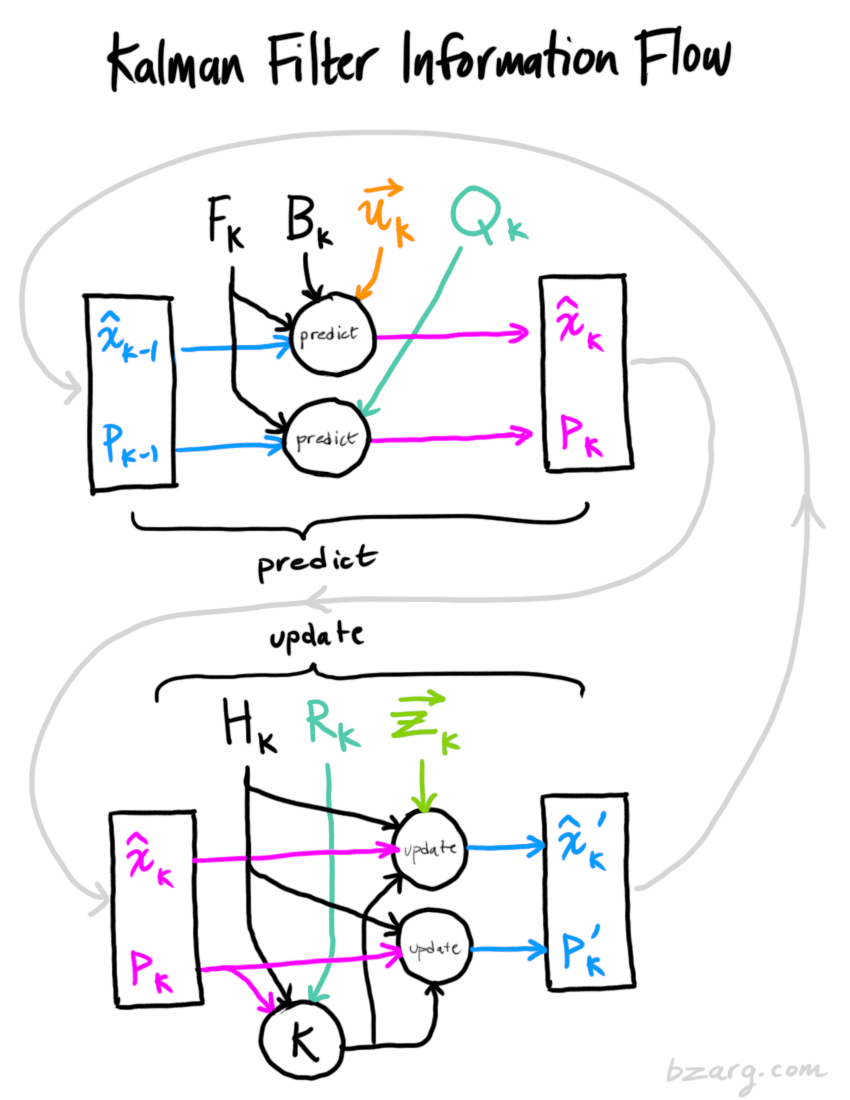
卡尔曼滤波浅析
文章目录前言任务状态预测外部影响因素外部不确定性状态更新利用测量进一步修正状态合并两个高斯分布公式汇总图形化解释总结(readme)references前言 Kalman Filter算法,是一种递推预测滤波算法,算法中涉及到滤波,也涉…...

Eolink Apikit 创建/生成 API 文档
在 API 研发管理产品中,几乎所有的协作工作都是围绕着 API 文档进行的。 我们在接触了大量的客户后发现,采用 文档驱动 的协作模式会比先开发、后维护文档的方式更好,团队协作效率和产品质量都能得到提高。因此我们建议您尝试基于文档来进行工…...

2023年上半年系统分析师备考法则
截止3月30日,上海、北京等地都开始报名,部分省市已经截止报名,大家如果还没报名成功的赶紧报名,千万别错过了,另外就是别忘了缴费,缴费成功才是报名成功。 报名网址:https://bm.ruankao.org.cn…...

【人工智能】—约束传播、弧约束、问题结果与问题分解、局部搜索CSP
【人工智能】—约束传播、弧约束、问题结果与问题分解、局部搜索CSP约束传播弧约束弧相容算法AC-3问题结构化简约束图-树结构CSP问题的局部搜索CSP的迭代算法举例:4-Queens加速:模拟退火法加速:最小最大优化(约束加权法)小结约束传播 前向检…...

Java设计模式面试专题
1.请列举出在 JDK 中几个常用的设计模式? 单例模式(Singleton pattern)用于 Runtime,Calendar 和其他的一些类中。工厂模式(Factory pattern)被用于各种不可变的类如 Boolean,像 Boolean.value…...

文件(下)——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是文件的知识点,下面,就让我们进入文件的世界吧 文件的顺序读写 文件的随机读写 fseek ftell rewind 文本文件和二进制文件 文件读取结束的判定 文件缓冲区 在上篇博客中,…...
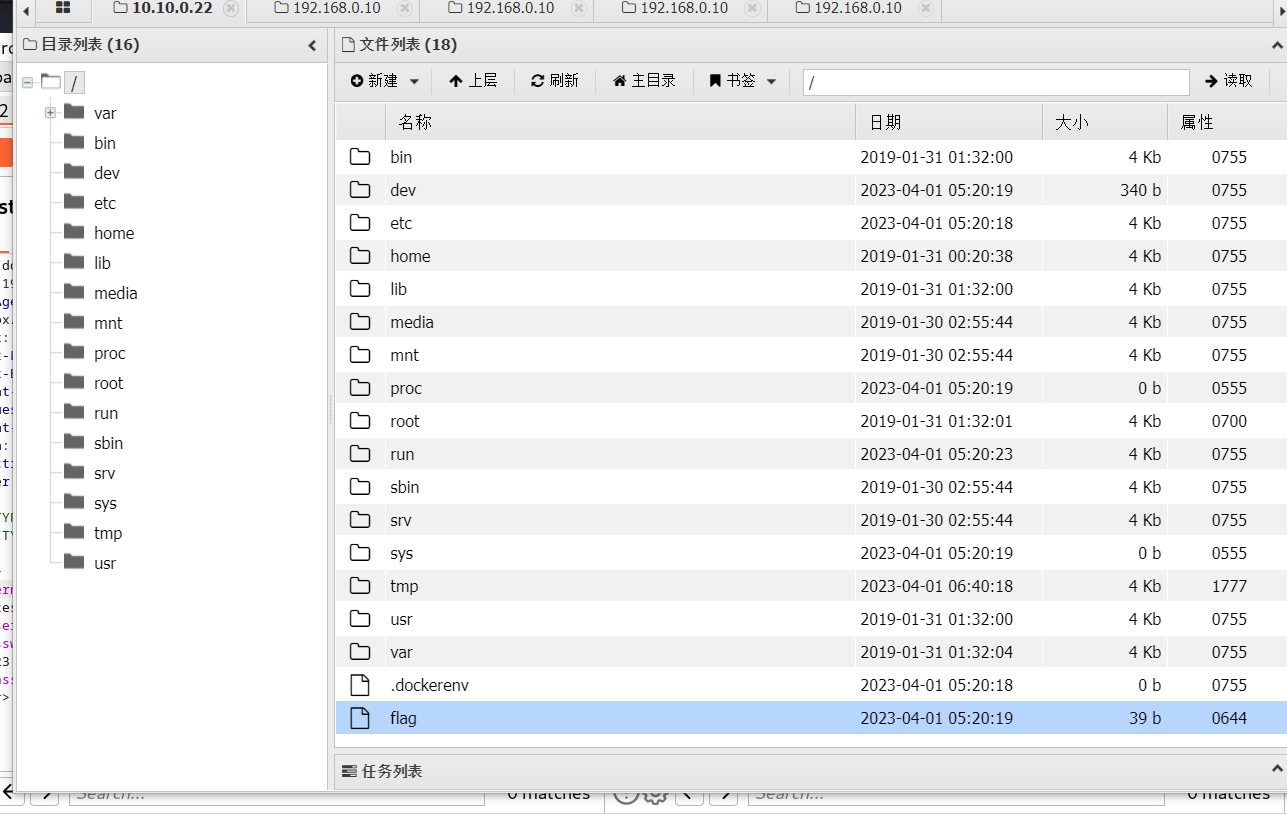
bugku 渗透靶场3
前言 本题一共八个flag,主要是为了练习内网渗透的思路。 解题思路 首先给了一个站长之家-模拟蜘蛛爬取,这个以前见到过,存在sstf漏洞,直接读取文件。 file:///flag既然是要内网渗透,那肯定要看/etc/hosts。 file:…...
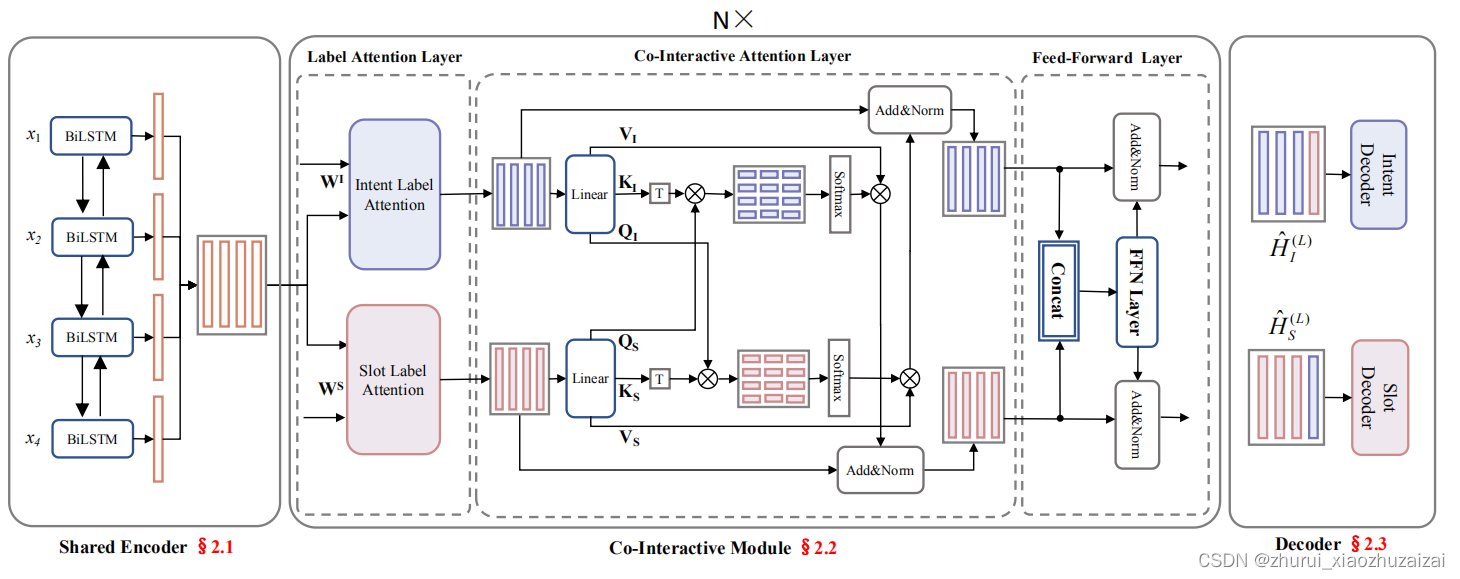
NER 任务以及联合提槽任务
KBERT 论文:《K-BERT: Enabling Language Representation with Knowledge Graph》 论文地址:https://arxiv.org/pdf/1909.07606v1 git地址:https://github.com/autoliuweijie/K-BERT SoftLexicon 出自ACL 2020的Simplify the Usage of Lexic…...

scala函数式编程
目录 不同范式对比: 1.面向对象编程 2.函数式编程 2.1函数基本语法 2.2函数和方法的区别 核心概念: 2.3函数定义 2.4函数参数 2.5 函数至简原则 2.6.高阶函数 三.偏函数 四.柯里化函数 五.递归函数 递归函数注意点: 六.控制抽象 1…...

网吧2023:热闹回来了,电竞战歌起
【潮汐商业评论/原创】 大年初四下午,人民公园附近尚未恢复往日热闹,上海网鱼电竞负责人崔潇瀚驱车前往位于人广世贸商场的网鱼电竞。 与广场上三两路人行色匆匆相比,门店显得忙碌异常,前台的服务叫单声响个不停,员工…...

代码随想录算法训练营第五十九天|503.下一个更大元素II、42. 接雨水
LeetCode 503 下一个更大元素II 题目链接:https://leetcode.cn/problems/next-greater-element-ii/ 思路: 方法一:两个for循环遍历单调栈 第一个for循环确定数组中的某个值在右边有最大的数,第二个for循环是为了可以使数组变成循环数…...
9、简单功能分析
文章目录1、静态资源访问1.1、静态资源目录1.2、如果静态资源与controller资源重名1.3、改变默认的静态资源路径1.4、修改静态资源访问前缀1.5、webjar2、欢迎页支持3、自定义 Favicon4、静态资源配置原理4.1、与Web开发有关的相关自动配置类4.2、WebMvcAutoConfiguration 注解…...
如何发送和接收参数?五种参数传递方法
通常情况下,我们可以使用GET或POST来发送请求和数据,但GET和POST两种方法所携带的数据都是比较简单的数据,接下来在我们这个基础上,列举5种比较负责的参数传递方法,并对这些参数如何发送,后台改如何接收做详…...

蓝桥杯C/C++VIP试题每日一练之矩形面积交
💛作者主页:静Yu 🧡简介:CSDN全栈优质创作者、华为云享专家、阿里云社区博客专家,前端知识交流社区创建者 💛社区地址:前端知识交流社区 🧡博主的个人博客:静Yu的个人博客 🧡博主的个人笔记本:前端面试题 个人笔记本只记录前端领域的面试题目,项目总结,面试技…...
Spark大数据处理讲课笔记2.4 IDEA开发词频统计项目
文章目录零、本讲学习目标一、词频统计准备工作(一)启动集群的HDFS与Spark(二)在HDFS上准备单词文件二、本地模式执行Spark程序(一)创建Maven项目(二)添加Spark相关依赖,…...
【ChatGPT 】国内无需注册 openai 即可访问 ChatGPT:ChatGPT Sidebar 浏览器扩展程序的安装与使用
一、前言 问题:国内注册 openai 账号麻烦,新必应有部分人也无法登录成功,存在域名单点登录失败等问题,所以无法真正使用 ChatGPT 解决:大部分人仅需使用 ChatGPT 的搜索功能,无需真正对话,需要…...

使用fetch()异步请求API数据实现汇率转换器
任务8 https://segmentfault.com/a/1190000038998601 https://chinese.freecodecamp.org/news/how-to-master-async-await-with-this-real-world-example/ 跟随上面的指示,理解异步函数的编写,并且实现这个汇率转换器。 第一步:在工作区初始…...
GPT-4“王炸”,10秒钟开发一套Web + APP 系统
10秒钟做出一个网站 一则有关GPT4发布会的视频在网上流传,这则两分钟的视频演示的内容是: 1. 在草稿本上用纸笔画出一个非常粗糙的草图; 2. 拍照告诉 GPT 我们要做一个网站,效果正如图所示,让其生成网站代码࿱…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
