LeetCode-2608. 图中的最短环【广度优先搜索 图,腾讯面试真题】
LeetCode-2608. 图中的最短环【广度优先搜索 图,腾讯面试真题】
- 题目描述:
- 解题思路一:【一图秒懂】枚举起点跑 BFS
- 解题思路二:背诵版
- 解题思路三:
题目描述:
现有一个含 n 个顶点的 双向 图,每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接,并且不存在与自身相连的顶点。
返回图中 最短 环的长度。如果不存在环,则返回 -1 。
环 是指以同一节点开始和结束,并且路径中的每条边仅使用一次。
示例 1:

输入:n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
输出:3
解释:长度最小的循环是:0 -> 1 -> 2 -> 0
示例 2:

输入:n = 4, edges = [[0,1],[0,2]]
输出:-1
解释:图中不存在循环
提示:
2 <= n <= 1000
1 <= edges.length <= 1000
edges[i].length == 2
0 <= ui, vi < n
ui != vi
不存在重复的边
解题思路一:【一图秒懂】枚举起点跑 BFS
题解参考

问:为什么说发现一个已经入队的点,就说明有环?
答:这说明到同一个点有两条不同的路径,这两条路径组成了一个环。
class Solution:def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:g = [[] for _ in range(n)]for x, y in edges:g[x].append(y)g[y].append(x) # 建图def bfs(start):ans = infdis = [-1] * n # dis[i] 表示从start到i的最短路径长度dis[start] = 0q = deque([(start, -1)])while q:x, fa = q.popleft()for y in g[x]:if dis[y] < 0: # 第一次遇到dis[y] = dis[x] + 1q.append((y, x))elif y != fa: # 第二次遇到ans = min(ans, dis[x] + dis[y] + 1)return ansans = min(bfs(i) for i in range(n))return ans if ans < inf else -1时间复杂度:O(nm)
空间复杂度:O(n+m)
解题思路二:背诵版
class Solution:def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:g = [[] for _ in range(n)]for u, v in edges:g[u].append(v)g[v].append(u)def bfs(start):ans = infdis = [-1] * nq = deque([(start, -1)])dis[start] = 0while q:x, fa = q.popleft()for y in g[x]:if dis[y] < 0:dis[y] = dis[x] + 1q.append((y, x))elif y != fa:ans = min(ans, dis[x] + dis[y] + 1)return ansans = min(bfs(i) for i in range(n))return ans if ans < inf else -1
时间复杂度:O(nm)
空间复杂度:O(n+m)
解题思路三:
时间复杂度:O(n)
空间复杂度:O(n)



♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠
相关文章:

LeetCode-2608. 图中的最短环【广度优先搜索 图,腾讯面试真题】
LeetCode-2608. 图中的最短环【广度优先搜索 图,腾讯面试真题】 题目描述:解题思路一:【一图秒懂】枚举起点跑 BFS解题思路二:背诵版解题思路三: 题目描述: 现有一个含 n 个顶点的 双向 图,每个…...

IDEA 编译报错 “java: 常量字符串过长” 的解决办法
目录 一、问题描述二、问题原因2.1 理论角度2.2 源码角度 三、解决方案解决方案①:StringBuilder 拼接解决方案②:读取文件内容 四、方案验证 在线文本换行工具: https://lzltool.cn/Toolkit/WrapWordsInText 一、问题描述 今天在开发过程中…...

RK3568平台开发系列讲解(I2C篇)I2C 总线实现 client 设备方法
🚀返回专栏总目录 文章目录 一、非设备树实现 i2c client1.1、i2c_new_device1.2、i2c client二、设备树实现 i2c2.1、i2c_client 结构体的生成2.2、i2c_driver 驱动2.2.1、module_i2c_driver2.2.2、fan53555_regulator_probe沉淀、分享、成长,让自己和他人都能有所收获!�…...

K8S安装和部署
环境部署说明 主机IPmaster172.25.254.100node10172.25.254.10node20172.25.254.20harbor172.25.254.233 所有节点禁用selinux和防火墙 所有节点同步时间和解析 所有节点安装docker-ce 所有节点禁用swap,注意注释掉/etc/fstab文件中的定义 解析配置(…...
)
Singleton(单例模式)
1. 意图 在开发中,若某些模块或功能只需要一个类实例,所有调用地方通过着一个类对象访问功能,单例模式符合这种类实例创建模式,并且通过提供统一类实例接口访问类对象。 2. 适用性 《Gof 设计模式-可复用面向对象软件的基础》中对…...

【Linux报错】“-bash: cd: too many arguments“
问题描述 今天使用 cd 想要调整某个文件目录时,发现以下报错 原因分析: arguments 是参数的意思,该报错提示参数过多,意味着系统识别到了多余参数 本质原因:你的命令中输入了多余的 ”空格“ ,检查一…...

C# WebService返回参数为DataTable报错“XML文档有错误”
该问题由于DataTable列存在自定义类型。 解决该报错需要以下几步: 1、自定义类型增加xml序列化 2、由于C#从 XML 反序列化 DataSet 或 DataTable 时的默认限制,所以需要先把调用方的项目开放限制,如果是.netframework项目,需要…...
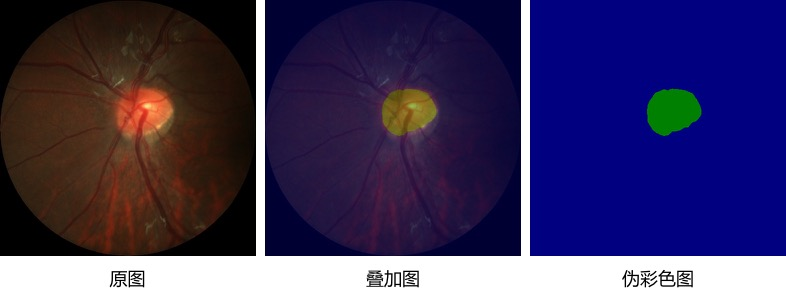
[paddle]paddleseg快速开始
快速开始 为了让大家快速了解PaddleSeg,本文档使用一个简单示例进行演示。在实际业务中,建议大家根据实际情况进行调整适配。 在开始下面示例之前,请大家确保已经安装好PaddleSeg开发环境(安装说明)。 1 准备数据 …...

UNIAPP popper气泡弹层【unibest框架下】vue3+typescript
看了下市场的代码,要么写的不怎么好,要么过于复杂。于是把市场的代码下下来了自己改。200行代码撸了个弹出层组件。兼容H5和APP。 功能: 1)只支持上下左右4个方向的弹层不支持侧边靠齐 2)不对屏幕边界适配 3)支持弹层外边点击自动隐藏 4)支持…...

launcher.py: error: the following arguments are required: --output_dir
记录一个LLaMA-Factroy配置过程。 安装 git clone --depth 1 https://github.com/hiyouga/LLaMA-Factory.git cd LLaMA-Factory pip install -e ".[torch,metrics]"训练 CUDA_VISIBLE_DEVICES0 llamafactory-cli train example/train_lora/.yaml按理说配置好文件应…...

C语言基础之结构体
今天我们来讲讲C语言基础的最后一个知识点了 —— 结构体。不知道大家对前面的C语言基础的知识点掌握的怎么样了呢?下面我们就开始讲解结构体的相关知识点吧! 什么是结构体呢?或者说结构体有什么作用呢?对于复杂对象来说ÿ…...

Redis入门第四步:Redis发布与订阅
欢迎继续跟随《Redis新手指南:从入门到精通》专栏的步伐!在本文中,我们将深入探讨Redis的发布与订阅(Pub/Sub)模式。这是一种强大的消息传递机制,适用于各种实时通信场景,如聊天应用、实时通知和…...

MySQL 之权限与授权
MySQL 权限及授权系统用于控制数据库用户对数据库资源的访问和操作权限。它提供了一种细粒度的安全控制机制,确保只有被授权的用户才能执行特定的操作。MySQL 的权限控制体系非常灵活,支持多种权限类型及级别(数据库、表、列、存储过程等&…...

解决方案:Pandas里面的loc跟iloc,有什么区别
文章目录 一、现象二、解决方案案例使用loc使用iloc 简单总结 一、现象 在用Pandas库处理数据的时候,久而久之不用loc跟iloc,难免会有些混乱记混 二、解决方案 在Pandas中,loc和iloc是两种常用的数据选择方法,它们的主要区别在…...

C# 和 C++ 混合编程
以下是一个关于 C# 和 C 混合编程 的教程详细目录,涵盖了混合编程中的各个重要方面: 目录 1. 引言 1.1 什么是混合编程? 1.2 为什么选择 C# 和 C 进行混合编程? 1.3 应用场景和优势 2. 基本概念 2.1 C# 和 C 的基础差异 2.…...

Vxe UI vue vxe-table 实现表格单元格选中功能
Vxe UI vue vxe-table 实现表格单元格选中功能 在表格中实现鼠标点击任意单元格,选取的功能,通过 mouse-config 配置就可以开启单选功能,多选单元格选取功能需安装插件支持。 代码 参数说明 mouse-config 鼠标配置项: selected&…...

组合模式详解
1、组合模式基本介绍 1) 组合模式(Composite Pattern),又叫部分整体模式,它创建了对象组的树形结构,将对象组合成树状结构以 表示“整体-部分”的层次关系。 2) 组合模式依据树形结构来组合对象,用来表示部…...
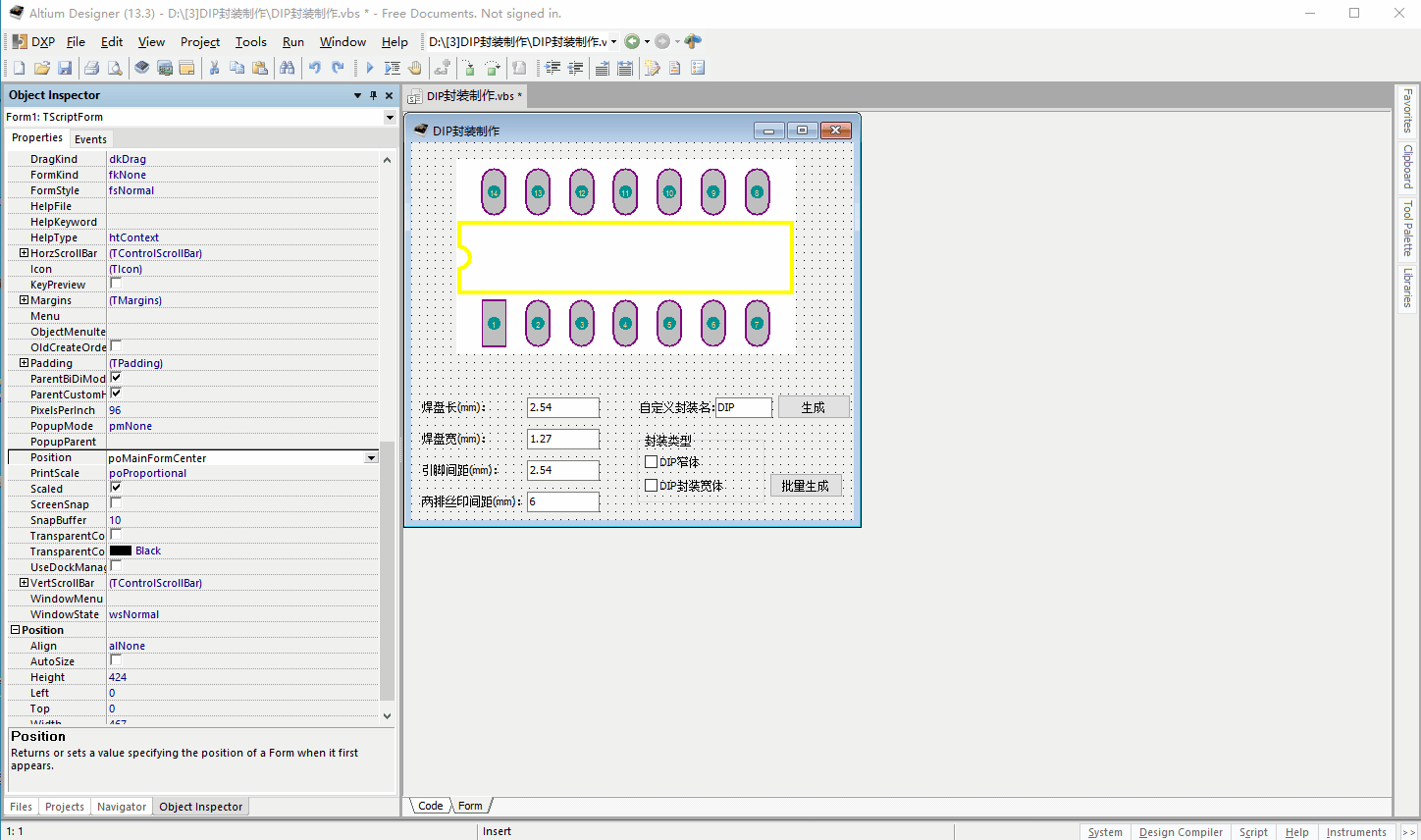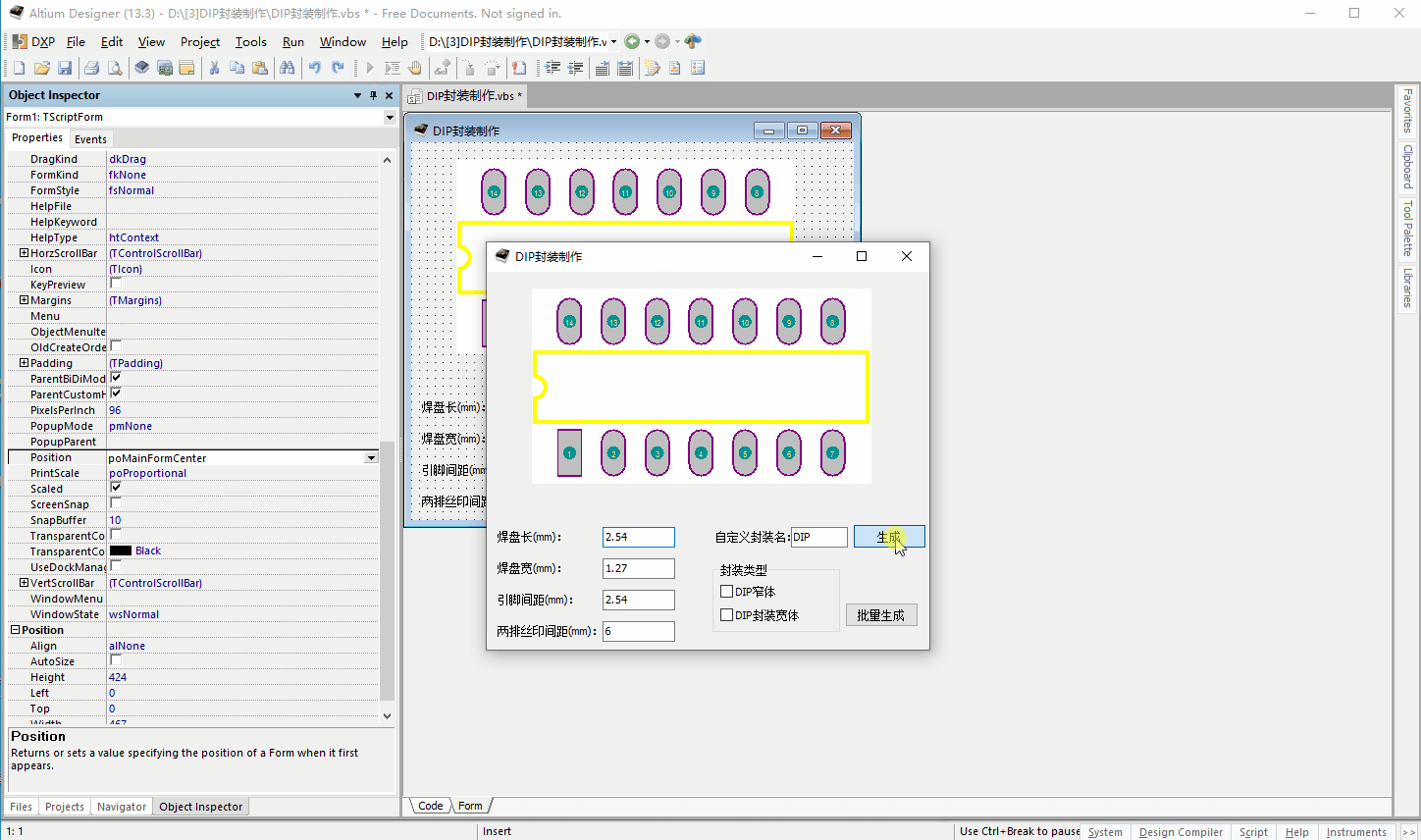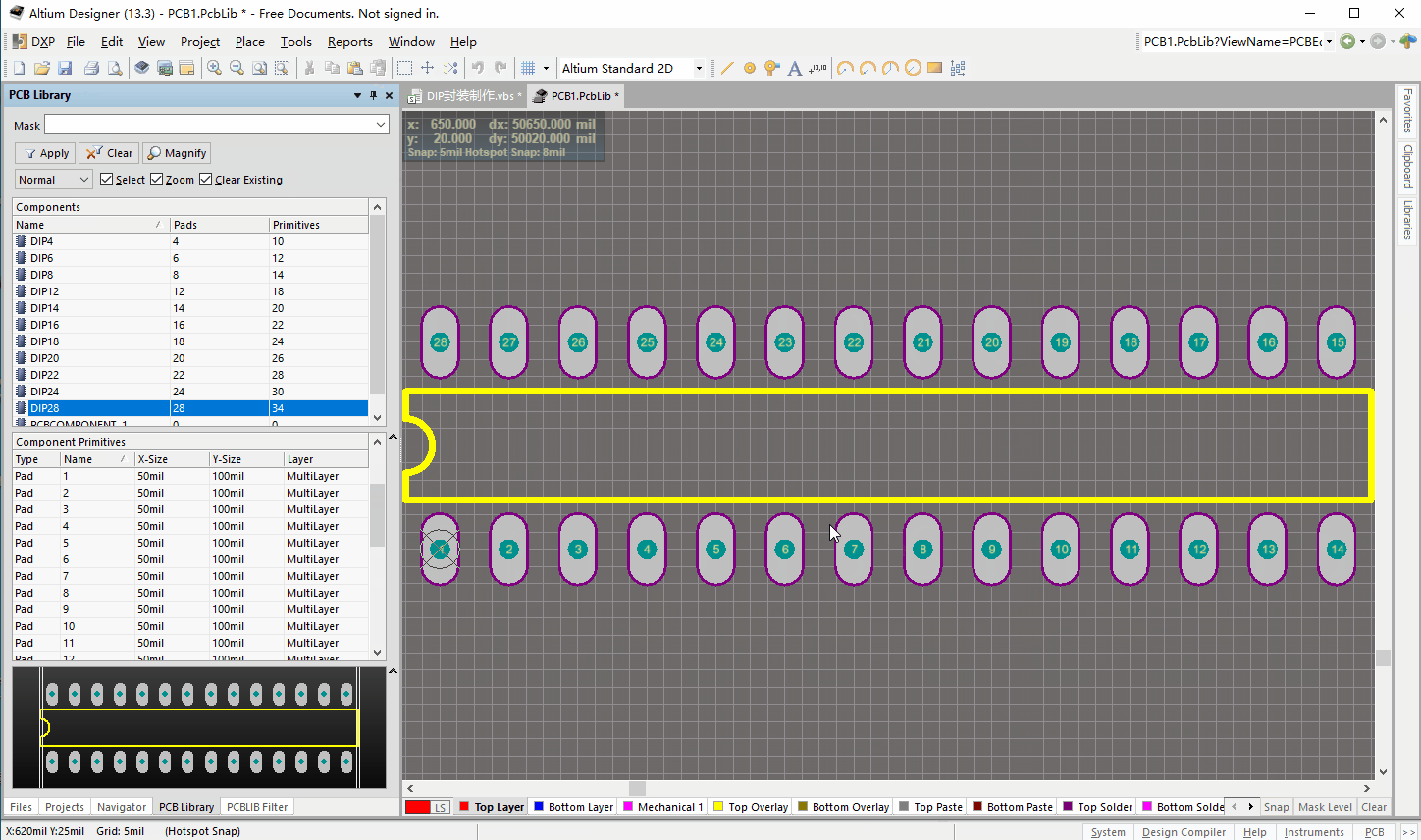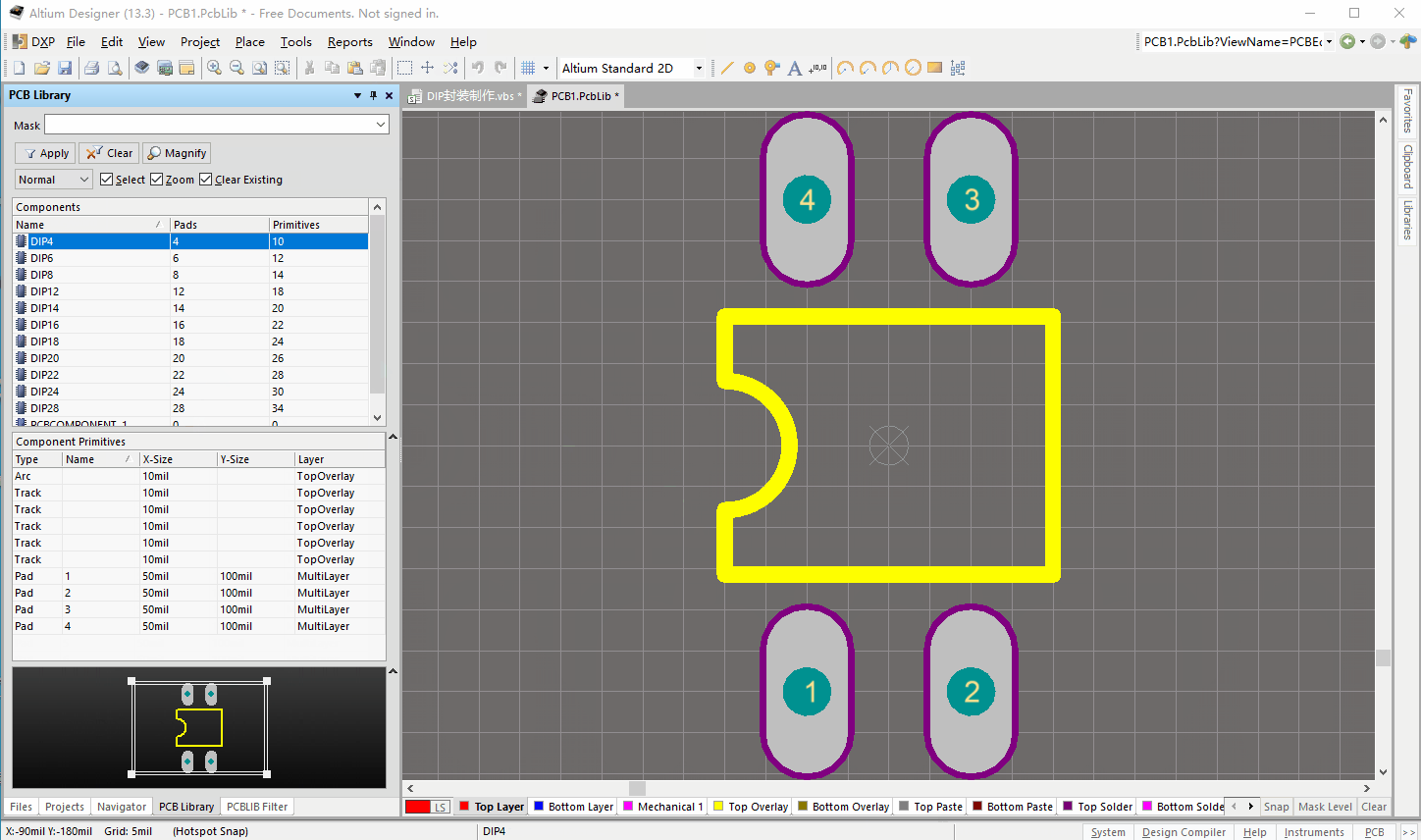
AltiumDesigner脚本开发-DIP封装制作
1.点击工具栏的运行工具(蓝色向右三角图标)可以执行脚本程序; 2.点击菜单栏Run->Run可以执行脚本程序; 3.在脚本编辑器中,按键盘的F9键可以执行脚本程序; 4.通过菜单栏执行脚本程序(需要将程序添加到菜单栏中&am…...

乌班图基础设施安装之Mysql8.0+Redis6.X安装
简介:云服务器基础设施安装之 Mysql8.0Redis6.X 安装 Docker安装 # 按照依赖 yum install -y yum-utils device-mapper-persistent data lvm2 Docker Mirror 从去年开始. hub.docker.com[1] 在国内的访问速度极慢. 当时大家主要还是依赖国内的一些镜像源: 如中科…...

【动态规划-最长递增子序列(LIS)】力扣673.最长递增子序列的个数
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数 。 注意 这个数列必须是 严格 递增的。 示例 1: 输入: [1,3,5,4,7] 输出: 2 解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。 示例 2: 输入: [2,2,2,2,2] 输出: 5 解释:…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
